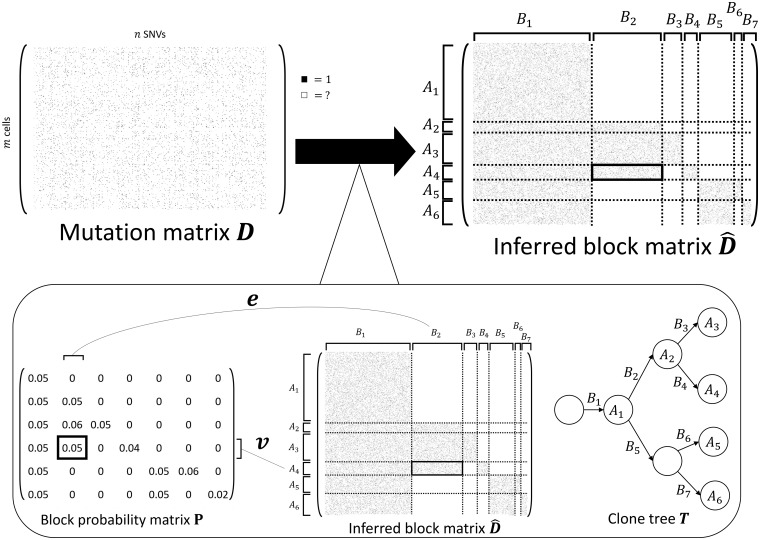
Fig. 1.

SBMClone solves the CBI problem using an SBM. (Top) An example mutation matrix D with m cells (rows) and n mutations (columns) is composed of entries with either 1 or ‘?’ to indicate the measurement (black square) or lack of measurement (white square) of a mutation in each cell. The goal of the CBI problem is to infer the rearrangement of the rows and columns of D that form the inferred block matrix ${\widehat{D}}_{k,\ell }$ where rows are partitioned into k row blocks $A_1,\dots ,A_k$ (k = 6 here), columns are partitioned into $\ell$ column blocks $B_1,\dots ,B_{\ell }$ ($\ell =7$ here), and each block of $\widehat{D}$ has either high (many black squares) or low (no black squares) proportions of 1s. (Bottom left) SBMClone uses an SBM which is a generative model parameterized by the block probability matrix $P=[p_{r,s}]$. Each block probability $p_{r,s}$ indicates the expected proportion of 1s within the block composed of the cells in row block A_r and the mutations in column block B_s. (Bottom right) The mutation matrix D has a block structure because every row block A_r corresponds to a clone, which accumulate clusters of mutations that correspond to every column block B_s; this evolutionary process is described as the clone tree T where every node correspond to a clone and every edge is labeled by a mutation cluster