Fig. 1.

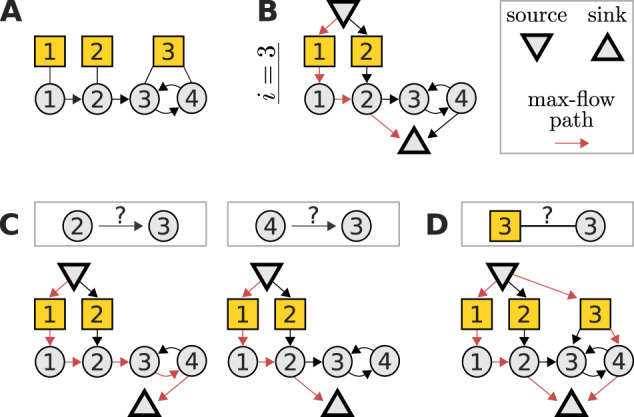
A maximum-flow problem determines the identifiability of interaction strengths and perturbation sensitivities when reconstructing a network from perturbation data. (A) Example network with three perturbations (yellow squares) to illustrate the algorithm. (B) The corresponding flow network to determine the identifiability of the edges into node 3 and the sensitivity of node 3 to perturbations. The flow passing through any node (besides source and sink) must not exceed one. A path carrying the resulting maximal flow of one is denoted in red (note that it is not unique). (C) The interaction strength between a given node and node 3 is identifiable if and only if the maximum flow is reduced after removing that node’s edge to the sink node. In this example, there are alternative max-flow paths that re-establish a unit-flow after removal of the according edges. Thus, the respective interaction strengths are non-identifiable. (D) Similarly, the sensitivity of node 3 to perturbation 3 is identifiable, if and only if the depicted extension of the flow network does not increase the maximum flow. In this example, the maximum flow is increased by one, again revealing non-identifiability. Note that such flow representations provide an intuitive understanding on how alterations in the network or perturbation setting affect identifiability. For example, it is obvious that if the toy model would not contain an edge from node 3 to 4, the edge from 2 to 3 would become identifiable