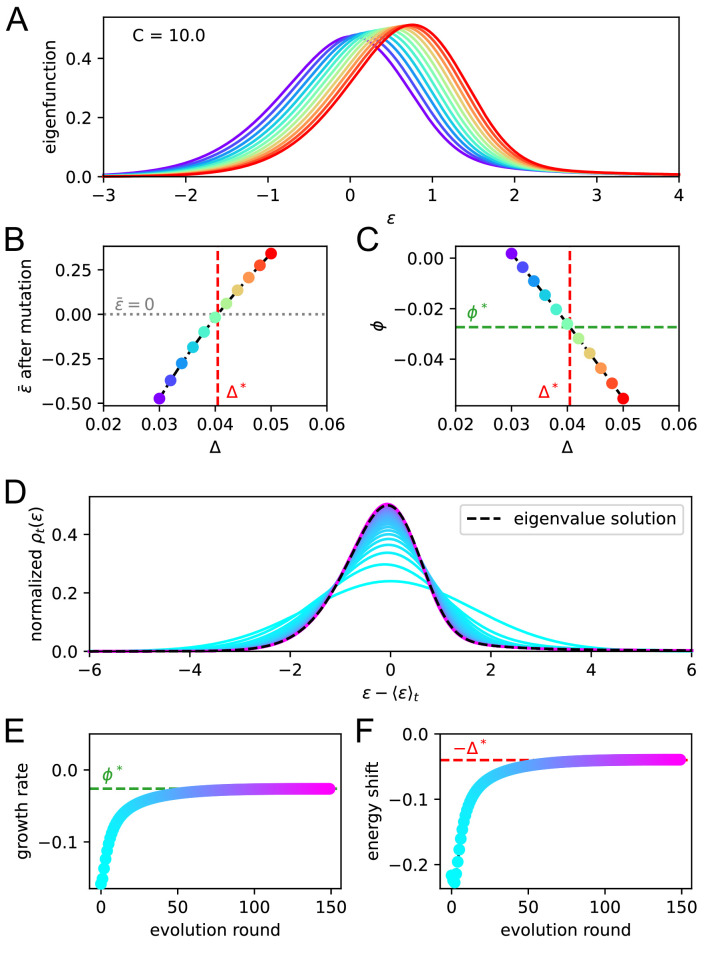
Appendix 1—figure 4. Asymptotic evolution matches the solution of the eigenvalue equation.

We check that upon repetition of the evolution operator the system converges at the eigenvalue equation solution. For a given constant Ag concentration ($C=10$ in our case) we solve the eigenvalue equation $e^{\varphi }\rho =\mathbf{𝚺}(-\mathrm{\Delta })\mathbf{𝐄}\rho$ for various values of the shift $\mathrm{\Delta }$. In A we report the maximum eigenvalue eigenfunctions. By virtue of the Perron-Frobenius theorem these consist of only positive values. Color represent the value of the shift $\mathrm{\Delta }$ for the corresponding solution. In B and C, we plot the value of $\overline{ϵ}$ after mutation and of the growth rate $\varphi$ for every solution. The consistency condition requires us to pick the eigenfunction for whom the value of $\overline{ϵ}$ after mutation is zero. This corresponds to the value ${\mathrm{\Delta }}^{*}$ represented in vertical red dashed line and the value of the growth rate ${\varphi }^{*}$ in horizontal green dashed line. In panels D, E, F, we consider repeated application of the evolution operator to the binding energy distribution at constant Ag concentration $C=10$. Color encodes the number of applications of this operator. In D and E, we report respectively the growth rate and shift of the mean per evolution turn, and in F the full distribution of binding energies, normalized to the population size. All the quantities converge to their theoretical expectation given by the chosen solution of the eigenvalue equation, reported as green and red dashed lines.