Abstract
We introduce and study good-enough synthesis (ge-synthesis) – a variant of synthesis in which the system is required to satisfy a given specification  only when it interacts with an environments for which a satisfying interaction exists. Formally, an input sequence x is hopeful if there exists some output sequence y such that the induced computation
only when it interacts with an environments for which a satisfying interaction exists. Formally, an input sequence x is hopeful if there exists some output sequence y such that the induced computation  satisfies
satisfies  , and a system ge-realizes
, and a system ge-realizes 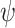 if it generates a computation that satisfies
if it generates a computation that satisfies  on all hopeful input sequences. ge-synthesis is particularly relevant when the notion of correctness is multi-valued (rather than Boolean), and thus we seek systems of the highest possible quality, and when synthesizing autonomous systems, which interact with unexpected environments and are often only expected to do their best.
on all hopeful input sequences. ge-synthesis is particularly relevant when the notion of correctness is multi-valued (rather than Boolean), and thus we seek systems of the highest possible quality, and when synthesizing autonomous systems, which interact with unexpected environments and are often only expected to do their best.
We study ge-synthesis in Boolean and multi-valued settings. In both, we suggest and solve various definitions of ge-synthesis, corresponding to different ways a designer may want to take hopefulness into account. We show that in all variants, ge-synthesis is not computationally harder than traditional synthesis, and can be implemented on top of existing tools. Our algorithms are based on careful combinations of nondeterministic and universal automata. We augment systems that ge-realize their specifications by monitors that provide satisfaction information. In the multi-valued setting, we provide both a worst-case analysis and an expectation-based one, the latter corresponding to an interaction with a stochastic environment.
Introduction
Synthesis is the automated construction of a system from its specification: given a specification  , typically by a linear temporal logic (LTL) formula over sets I and O of input and output signals, the goal is to construct a finite-state system that satisfies
, typically by a linear temporal logic (LTL) formula over sets I and O of input and output signals, the goal is to construct a finite-state system that satisfies  [9, 20]. At each moment in time, the system reads an assignment, generated by the environment, to the signals in I, and responds with an assignment to the signals in O. Thus, with every input sequence, the system associates an output sequence. The system realizes
[9, 20]. At each moment in time, the system reads an assignment, generated by the environment, to the signals in I, and responds with an assignment to the signals in O. Thus, with every input sequence, the system associates an output sequence. The system realizes
 if
if 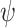 is satisfied in all the interactions of the system, with all environments
[5].
is satisfied in all the interactions of the system, with all environments
[5].
In practice, the requirement to satisfy the specification in all environments is often too strong. Accordingly, it is common to add assumptions on the behavior of the environment. An assumption may be direct, say given by an LTL formula that restricts the set of possible input sequences [8], less direct, say a bound on the size of the environment [13] or other resources it uses, or conceptual, say rationality from the side of the environment, which may have its own objectives [11, 14]. We introduce and study a new type of relaxation of the requirement to satisfy the specification in all environments. The idea behind the relaxation is that if an environment is such that no system can interact with it in a way that satisfies the specification, then we cannot expect our system to succeed. In other words, the system has to satisfy the specification only when it interacts with environments in which this mission is possible. This is particularly relevant when synthesizing autonomous systems, which interact with unexpected environments and often replace human behavior, which is only expected to be good enough [28], and when the notion of correctness is multi-valued (rather than Boolean), and thus we seek high-quality systems.
Before we explain the relaxation formally, let us consider a simple example, and we start with the Boolean setting. Let  and
and  . Thus, the system receives requests and generates grants. Consider the specification
. Thus, the system receives requests and generates grants. Consider the specification 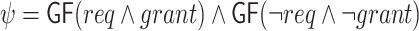 . Clearly,
. Clearly, 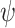 is not realizable, as an input sequence need not satisfy
is not realizable, as an input sequence need not satisfy  or
or  . However, a system that always generates a grant upon (and only upon) a request, ge
-realizes
. However, a system that always generates a grant upon (and only upon) a request, ge
-realizes
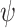 , in the sense that for every input sequence, if there is some interaction with it with which
, in the sense that for every input sequence, if there is some interaction with it with which 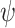 is satisfied, then our system generates such an interaction.
is satisfied, then our system generates such an interaction.
Formally, we model a system by a strategy  , which given an input sequence
, which given an input sequence 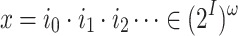 , generates an output sequence
, generates an output sequence 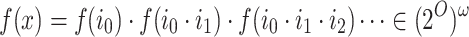 , inducing the computation
, inducing the computation  , obtained by “merging” x and f(x). In traditional realizability, a system realizes
, obtained by “merging” x and f(x). In traditional realizability, a system realizes 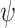 if
if 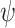 is satisfied in all environments. Formally, for all input sequences
is satisfied in all environments. Formally, for all input sequences  , the computation
, the computation 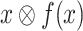 satisfies
satisfies 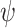 . For our new notion, we first define when an input sequence
. For our new notion, we first define when an input sequence  is hopeful, namely there is an output sequence
is hopeful, namely there is an output sequence  such that the computation
such that the computation  satisfies
satisfies 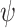 . Then, a system ge
-realizes
. Then, a system ge
-realizes
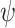 if
if  is satisfied in all interactions with hopeful input sequences. Formally, for all
is satisfied in all interactions with hopeful input sequences. Formally, for all  , if x is hopeful, then the computation
, if x is hopeful, then the computation 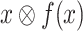 satisfies
satisfies 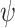 .
.
Since LTL is Boolean, synthesized systems are correct, but there is no reference to their quality. This is a crucial drawback, as designers would be willing to give up manual design only if automated-synthesis algorithms return systems of comparable quality. Addressing this challenge, researchers have developed quantitative specification formalisms. For example, in
[4], the input to the synthesis problem includes also Mealy machines that grade different realizing systems. In
[1], the specification formalism is the multi-valued logic  , which augments
, which augments  with quality operators. The satisfaction value of an
with quality operators. The satisfaction value of an  formula is a real value in [0, 1], where the higher the value, the higher the quality in which the computation satisfies the specification. The quality operators in
formula is a real value in [0, 1], where the higher the value, the higher the quality in which the computation satisfies the specification. The quality operators in  can prioritize and weight different scenarios. The synthesis algorithm for
can prioritize and weight different scenarios. The synthesis algorithm for  seeks systems with a highest possible satisfaction value. One can consider either a worst-case approach, where the satisfaction value of a system is the satisfaction value of its computation with the lowest satisfaction value
[1], or a stochastic approach, where it is the expected satisfaction value, given a distribution of the inputs
[2].
seeks systems with a highest possible satisfaction value. One can consider either a worst-case approach, where the satisfaction value of a system is the satisfaction value of its computation with the lowest satisfaction value
[1], or a stochastic approach, where it is the expected satisfaction value, given a distribution of the inputs
[2].
Consider, for example, an acceleration controller of an autonomous car. Normally, the car should maintain a relatively constant speed. However, in order to optimize travel time, if a long stretch of road is visible and is identified as low-risk, the car should accelerate. Conversely, if an obstacle or some risk factor is identified, the car should decelerate. Clearly, the car cannot accelerate and decelerate at the same time. We capture this desired behavior with the following  formula over the inputs
formula over the inputs  and outputs
and outputs  :
:
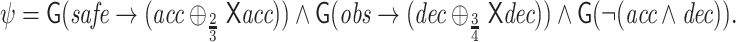 |
Thus, in order to get satisfaction value 1, each detection of a safe stretch should be followed by an acceleration during two transactions, with a preference to the first (by the semantics of the weighted average  operator, the satisfaction value of
operator, the satisfaction value of  is 1 when
is 1 when 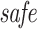 is followed by two
is followed by two  s,
s,  when it is followed by one
when it is followed by one  , and
, and  if it is followed by one
if it is followed by one  with a delay), and each detection of an obstacle should be followed by a deceleration during two transactions, with a (higher) preference to the first. Clearly,
with a delay), and each detection of an obstacle should be followed by a deceleration during two transactions, with a (higher) preference to the first. Clearly,  is not realizable with satisfaction value 1, as for some input sequences, namely those with simultaneous or successive occurrences of safe and obs, it is impossible to respond with the desired patterns of acceleration or declaration. Existing frameworks for synthesis cannot handle this challenge. Indeed, we do not want to add an assumption about safe and obs occurring far apart. Rather, we want our autonomous car to behave in an optimal way also in problematic environments, and we want, when we evaluate the quality of a car, to take into an account the challenge posed by the environment. This is exactly what high-quality ge-synthesis does: for each input sequence, it requires the synthesized car to obtain the maximal satisfaction value that is possible for that input sequence.
is not realizable with satisfaction value 1, as for some input sequences, namely those with simultaneous or successive occurrences of safe and obs, it is impossible to respond with the desired patterns of acceleration or declaration. Existing frameworks for synthesis cannot handle this challenge. Indeed, we do not want to add an assumption about safe and obs occurring far apart. Rather, we want our autonomous car to behave in an optimal way also in problematic environments, and we want, when we evaluate the quality of a car, to take into an account the challenge posed by the environment. This is exactly what high-quality ge-synthesis does: for each input sequence, it requires the synthesized car to obtain the maximal satisfaction value that is possible for that input sequence.
We show that in the Boolean setting, ge-synthesis can be reduced to synthesis of LTL with quantification of atomic propositions
[26]. Essentially, ge-synthesis of 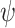 amounts to synthesis of
amounts to synthesis of  . We show that by carefully switching between nondeterminisitc and universal automata, we can solve the ge-synthesis problem in doubly-exponential time, thus it is not harder than traditional synthesis. Also, our algorithm is Safraless, thus no determinization and parity games are needed
[15, 17].
. We show that by carefully switching between nondeterminisitc and universal automata, we can solve the ge-synthesis problem in doubly-exponential time, thus it is not harder than traditional synthesis. Also, our algorithm is Safraless, thus no determinization and parity games are needed
[15, 17].
A drawback of ge-synthesis is that we do not actually know whether the specification is satisfied. We describe two ways to address this drawback. The first goes beyond providing satisfaction information and enables the designer to partition the specification into a strong component, which is guaranteed to be satisfied in all environments, and a weak component, which is guaranteed to be satisfied only in hopeful ones. The second way augments ge-realizing systems by “satisfaction indicators”. For example, we show that when a system is lucky to interact with an environment that generates a prefix of an input sequence such that, when combined with a suitable prefix of an output sequence, the specification becomes realizable, then ge-synthesis guarantees that the system indeed responds with a suitable prefix of an output sequence. Moreover, it is easy to add to the system a monitor that detects such prefixes, thus indicating that the specification is going to be satisfied in all environments. Additional monitors we suggest detect prefixes after which the satisfaction becomes valid or unsatisfiable.
We continue to the quantitative setting. We parameterize hope by a satisfaction value  and say that an input sequence
and say that an input sequence  is v-hopeful for an
is v-hopeful for an  formula
formula 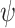 if an interaction with it can generate a computation that satisfies
if an interaction with it can generate a computation that satisfies 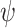 with value at least v. Formally, there is an output sequence
with value at least v. Formally, there is an output sequence  such that
such that  , where for a computation
, where for a computation 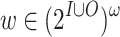 , we use
, we use 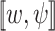 to denotes the satisfaction value of
to denotes the satisfaction value of 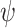 in w. As we elaborate below, while the basic idea of ge-synthesis, namely “input sequences with a potential to high quality should realize this potential” is as in the Boolean setting, there are several ways to implement this idea.
in w. As we elaborate below, while the basic idea of ge-synthesis, namely “input sequences with a potential to high quality should realize this potential” is as in the Boolean setting, there are several ways to implement this idea.
We start with a worst-case approach. There, a strategy 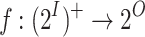 ge-realizes an
ge-realizes an  formula
formula 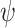 if for all input sequences
if for all input sequences  , if x is v-hopeful, then
, if x is v-hopeful, then 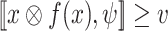 . The requirement can be applied to a threshold value or to all values
. The requirement can be applied to a threshold value or to all values  . For example, our autonomous car controller has to achieve satisfaction value 1 in roads with no simultaneous or successive occurrences of safe and obs, and value
. For example, our autonomous car controller has to achieve satisfaction value 1 in roads with no simultaneous or successive occurrences of safe and obs, and value  in roads that violate the latter only with some obs followed by safe. We then argue that the situation is similar to that of high-quality assume guarantee synthesis
[3], where richer relations between a quantitative assumption and a quantitative guarantee are of interest. In our case, the assumption is the hopefulness level of the input sequence, namely
in roads that violate the latter only with some obs followed by safe. We then argue that the situation is similar to that of high-quality assume guarantee synthesis
[3], where richer relations between a quantitative assumption and a quantitative guarantee are of interest. In our case, the assumption is the hopefulness level of the input sequence, namely 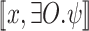 , and the guarantee is the satisfaction value of the specification in the generated computation, namely
, and the guarantee is the satisfaction value of the specification in the generated computation, namely  . When synthesizing, for example, a robot controller (e.g., vacuum cleaner) in a building, the doors to rooms are controlled by the environment, whereas the movement of the robot by the system. A measure of the performance of the robot has to take into an account both the number of “hopeful rooms”, namely these with an open door – a projection of this number on [0, 1] serves as the assumption, and the number of room cleaned – which induces the guarantee. We assume that the desired relation between the assumption and the guarantee is given by a function
. When synthesizing, for example, a robot controller (e.g., vacuum cleaner) in a building, the doors to rooms are controlled by the environment, whereas the movement of the robot by the system. A measure of the performance of the robot has to take into an account both the number of “hopeful rooms”, namely these with an open door – a projection of this number on [0, 1] serves as the assumption, and the number of room cleaned – which induces the guarantee. We assume that the desired relation between the assumption and the guarantee is given by a function  , which can capture implication, difference, or ratio.
, which can capture implication, difference, or ratio.
We continue with an analysis of the expected performance of the system. We do so by assuming a stochastic environment, with a known distribution on the input sequences. We introduce and study two measures for high-quality ge-synthesis in a stochastic environment. In the first, termed expected
ge
-synthesis, all input sequences are sampled, yet the satisfaction value in each input sequence takes its hopefulness level into account, for example by a  function as in the assume-guarantee setting. In the second, termed conditional expected
ge
-synthesis, only hopeful input sequences are sampled. For both approaches, our synthesis algorithm is based on the high-quality
function as in the assume-guarantee setting. In the second, termed conditional expected
ge
-synthesis, only hopeful input sequences are sampled. For both approaches, our synthesis algorithm is based on the high-quality  synthesis algorithm of
[2], which is based on an analysis of deterministic automata associated with the different satisfaction values of the
synthesis algorithm of
[2], which is based on an analysis of deterministic automata associated with the different satisfaction values of the  specification. Here too, the complexity stays doubly exponential. In addition, we extend the synthesized systems with guarantees for satisfaction and monitors indicating satisfaction in various satisfaction levels.
specification. Here too, the complexity stays doubly exponential. In addition, we extend the synthesized systems with guarantees for satisfaction and monitors indicating satisfaction in various satisfaction levels.
Preliminaries
Consider two finite sets I and O of input and output signals, respectively. For two words  and
and  , we define
, we define  as the word in
as the word in  obtained by merging x and y. Thus,
obtained by merging x and y. Thus, 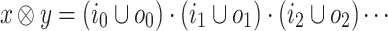 . The definition is similar for finite x and y of the same length. For a word
. The definition is similar for finite x and y of the same length. For a word 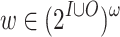 , we use
, we use 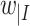 to denote the projection of w on I. In particular,
to denote the projection of w on I. In particular, 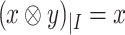 .
.
A strategy is a function 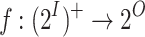 . Intuitively, f models the interaction of a system that generates in each moment in time a letter in
. Intuitively, f models the interaction of a system that generates in each moment in time a letter in  with an environment that generates letters in
with an environment that generates letters in  . For an input sequence
. For an input sequence  , we use f(x) to denote the output sequence
, we use f(x) to denote the output sequence  . Then,
. Then, 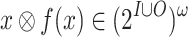 is the computation of f on x. Note that the environment initiates the interaction, by inputting
is the computation of f on x. Note that the environment initiates the interaction, by inputting 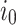 . Of special interest are finite-state strategies, induced by finite state transducers. Formally, an I/O-transducer is
. Of special interest are finite-state strategies, induced by finite state transducers. Formally, an I/O-transducer is 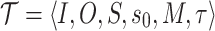 , where S is a finite set of states,
, where S is a finite set of states,  is an initial state,
is an initial state, 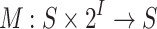 is a transition function, and
is a transition function, and  is a labelling function. For
is a labelling function. For 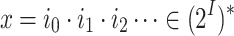 , let
, let 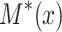 be the state in S that
be the state in S that  reaches after reading x. Thus is,
reaches after reading x. Thus is, 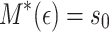 and for every
and for every 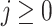 , we have that
, we have that  . Then,
. Then,  induces the strategy
induces the strategy  , where for every
, where for every  , we have that
, we have that  . We use
. We use  and
and 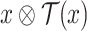 to denote the output sequence and the computation of
to denote the output sequence and the computation of  on x, respectively, and talk about
on x, respectively, and talk about  realizing a specification, referring to the strategy
realizing a specification, referring to the strategy  .
.
We specify on-going behaviors of reactive systems using the linear temporal logic LTL
[19]. Formulas of LTL are constructed from a set AP of atomic proposition using the usual Boolean operators and temporal operators like  (“always”),
(“always”),  (“eventually”),
(“eventually”),  (“next time”), and
(“next time”), and  (“until”). Each LTL formula
(“until”). Each LTL formula  defines a language
defines a language  . We also use automata on infinite words for specifying and reasoning about on-going behaviors. We use automata with different branching modes (nondeterministic, where some run has to be accepting; universal, where all runs have to be accepting; and deterministic, where there is a single run) and different acceptance conditions (Büchi, co-Büchi, and parity). We use the three letter acronyms NBW, UCW, DPW, and DFW, to refer to nondeterministic Büchi, universal co-Büchi, deterministic parity, and deterministic finite word automata, respectively. Given an LTL formula
. We also use automata on infinite words for specifying and reasoning about on-going behaviors. We use automata with different branching modes (nondeterministic, where some run has to be accepting; universal, where all runs have to be accepting; and deterministic, where there is a single run) and different acceptance conditions (Büchi, co-Büchi, and parity). We use the three letter acronyms NBW, UCW, DPW, and DFW, to refer to nondeterministic Büchi, universal co-Büchi, deterministic parity, and deterministic finite word automata, respectively. Given an LTL formula 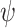 over AP, one can constructs an NBW
over AP, one can constructs an NBW  with at most
with at most  states such that
states such that  [27]. Constructing an NBW for
[27]. Constructing an NBW for  and then dualizing it, results in a UCW for
and then dualizing it, results in a UCW for 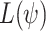 , also with at most
, also with at most  states. Determinization
[23] then leads to a DPW for
states. Determinization
[23] then leads to a DPW for  with at at most
with at at most  states and index
states and index 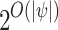 . For full definitions of LTL, automata, and their relation, see
[12].
. For full definitions of LTL, automata, and their relation, see
[12].
Consider an LTL formula 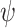 over
over 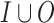 . We say that
. We say that 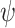 is realizable if there is a finite-state strategy
is realizable if there is a finite-state strategy 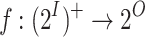 such that for all
such that for all  , we have that
, we have that 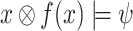 . That is, the computation of f on every input sequence satisfies
. That is, the computation of f on every input sequence satisfies 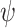 . We say that a word
. We say that a word  is hopeful for
is hopeful for 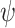 if there is
if there is  such that
such that  . Then, we say that
. Then, we say that 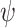 is good-enough realizable (ge-realizable, for short) if there is a finite-state strategy
is good-enough realizable (ge-realizable, for short) if there is a finite-state strategy 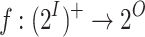 such that for every
such that for every  that is hopeful for
that is hopeful for 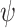 , we have that
, we have that 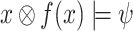 . That is, if there is some output sequence whose combination with x satisfies
. That is, if there is some output sequence whose combination with x satisfies  , then the computation of f on x satisfies
, then the computation of f on x satisfies  . The LTL ge-synthesis problem is then to decide whether a given LTL formula is ge-realizable, and if so, to return a transducer that ge-realizes it. Clearly, every realizable specification is ge-realizable – by the same transducer. We say that
. The LTL ge-synthesis problem is then to decide whether a given LTL formula is ge-realizable, and if so, to return a transducer that ge-realizes it. Clearly, every realizable specification is ge-realizable – by the same transducer. We say that 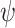 is universally satisfiable if all input sequences are hopeful for
is universally satisfiable if all input sequences are hopeful for 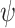 . It is easy to see that for universally satisfiable specifications, realizability and ge-realizability coincide. On the other hand, as demonstrated in Sect. 1, there are specifications that are not realizable and are ge-realizable.
. It is easy to see that for universally satisfiable specifications, realizability and ge-realizability coincide. On the other hand, as demonstrated in Sect. 1, there are specifications that are not realizable and are ge-realizable.
Example 1
Let 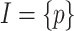 and
and  . Consider the specification
. Consider the specification 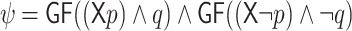 . Clearly,
. Clearly, 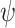 is not realizable, as an input sequence
is not realizable, as an input sequence  is hopeful for
is hopeful for 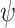 iff
iff 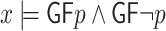 . Since the system has to assign a value to q before it knowns the value of
. Since the system has to assign a value to q before it knowns the value of 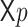 , it seems that
, it seems that 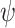 is also not ge-realizable. As we show below, however, the specification
is also not ge-realizable. As we show below, however, the specification 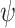 is ge-realizable. Intuitively, it follows from the fact that hopeful input sequences consists of alternating p-blocks and
is ge-realizable. Intuitively, it follows from the fact that hopeful input sequences consists of alternating p-blocks and 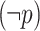 -blocks. Then, by outputting
-blocks. Then, by outputting  in p-blocks and outputting q in
in p-blocks and outputting q in  -blocks, the system guarantees that each last position in a
-blocks, the system guarantees that each last position in a  -block satisfies
-block satisfies  and each last position in a p-block satisfies
and each last position in a p-block satisfies  . Formally,
. Formally,  is ge-realized by the transducer
is ge-realized by the transducer  , where
, where  ,
,  ,
,  , and
, and 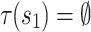 .
. 
LTL Good-Enough Synthesis
Recall that a strategy 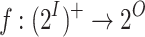 ge-realizes an LTL formula
ge-realizes an LTL formula 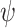 if its computations on all hopeful input sequences satisfy
if its computations on all hopeful input sequences satisfy  . Thus, for every input sequence
. Thus, for every input sequence  , either
, either 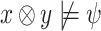 for all
for all 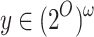 , or
, or 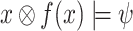 . The above suggests that algorithms for solving LTL ge-synthesis involve existential and universal quantification over the behavior of output signals. The logic EQLTL extends LTL by allowing existential quantification over atomic propositions
[26]. We refer here to the case the atomic propositions are the signals in
. The above suggests that algorithms for solving LTL ge-synthesis involve existential and universal quantification over the behavior of output signals. The logic EQLTL extends LTL by allowing existential quantification over atomic propositions
[26]. We refer here to the case the atomic propositions are the signals in  , and the signals in O are existentially quantified. Then, an EQLTL formula is of the form
, and the signals in O are existentially quantified. Then, an EQLTL formula is of the form  , and a computation
, and a computation 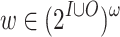 satisfies
satisfies 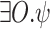 iff there is
iff there is  such that
such that  . Dually, AQLTL extends LTL by allowing universal quantification over atomic propositions. We consider here formulas of the form
. Dually, AQLTL extends LTL by allowing universal quantification over atomic propositions. We consider here formulas of the form 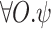 , which are equivalent to
, which are equivalent to 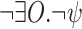 . Indeed, a computation
. Indeed, a computation 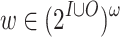 satisfies
satisfies 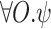 iff for all
iff for all  , we have that
, we have that 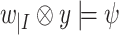 . Note that in both the existential and universal cases, the O-component of w is ignored. Accordingly, we sometimes interpret EQLTL and AQLTL formulas with respect to input sequences
. Note that in both the existential and universal cases, the O-component of w is ignored. Accordingly, we sometimes interpret EQLTL and AQLTL formulas with respect to input sequences  . Also note that both EQLTL and AQLTL increase the expressive power of LTL. For example, the EQLTL formula
. Also note that both EQLTL and AQLTL increase the expressive power of LTL. For example, the EQLTL formula  states that p holds in all even positions of the computation, which cannot be specified in LTL
[29].
states that p holds in all even positions of the computation, which cannot be specified in LTL
[29].
Theorem 1
The LTL ge-synthesis problem is 2EXPTIME-complete.
Proof
We start with the upper bound. Given an LTL formula 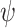 over
over 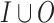 , we describe an algorithm that returns a transducer
, we describe an algorithm that returns a transducer  that ge-realizes
that ge-realizes 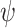 , or declares that no such transducer exists.
, or declares that no such transducer exists.
It is not hard to see that  ge-realizes
ge-realizes 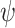 iff
iff  realizes
realizes  . Indeed, an input sequence
. Indeed, an input sequence  is hopeful for
is hopeful for 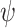 iff
iff  , and so the specification
, and so the specification 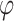 requires all hopeful input sequences to satisfy
requires all hopeful input sequences to satisfy  . A naive construction of an NBW for
. A naive construction of an NBW for 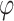 involves a universal projection of the signals in O in an automaton for
involves a universal projection of the signals in O in an automaton for  , and results in an NBW that is doubly exponential. In order to circumvent the extra exponent, we construct an NBW
, and results in an NBW that is doubly exponential. In order to circumvent the extra exponent, we construct an NBW  for
for 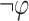 , and then dualize it to get a UCW for
, and then dualize it to get a UCW for 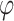 , as follows.
, as follows.
Let 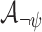 be an NBW for
be an NBW for 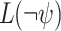 and
and  be an NBW for
be an NBW for  . Thus,
. Thus,  is obtained from an NBW
is obtained from an NBW  for
for  by existentially projecting its transitions on
by existentially projecting its transitions on  . In more details, if
. In more details, if 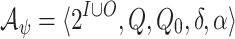 , then
, then 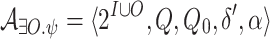 , where for all
, where for all  and
and  , we have
, we have 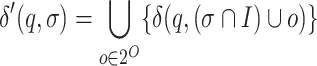 .
.
Let  be an NBW for the intersection of
be an NBW for the intersection of 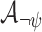 and
and  . We can define
. We can define  as the product of
as the product of 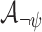 and
and  , possibly using the generalized Büchi acceptance condition (see Remark 1), thus its size is exponential in
, possibly using the generalized Büchi acceptance condition (see Remark 1), thus its size is exponential in  . The language of
. The language of 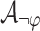 is then
is then 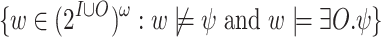 . We then solve usual synthesis for the complementing UCW. Its language is
. We then solve usual synthesis for the complementing UCW. Its language is  , as required. By
[17], the synthesis problem for UCW can be solved in EXPTIME, and we are done.
, as required. By
[17], the synthesis problem for UCW can be solved in EXPTIME, and we are done.
The lower bound follows from the 2EXPTIME-hardness of LTL realizability
[22]. The hardness proof there constructs, given a 2EXPTIME Turing machine M, an LTL formula  that is realizable iff M accepts the empty tape. Since all input sequences are hopeful for
that is realizable iff M accepts the empty tape. Since all input sequences are hopeful for 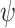 , realizability and ge-realizability coincide, and we are done.
, realizability and ge-realizability coincide, and we are done. 
Note that working with a UCW not only handles the universal quantification for free but also has the advantage of a Safraless synthesis algorithm – no determinization and parity games are needed [15, 17]. Also note that the algorithm we suggest in the proof of Theorem 1 can be generalized to handle specifications that are arbitrary positive Boolean combinations of EQLTL formulas.
Remark 1
[Products and optimizations]. Throughout the paper, we construct products of automata whose state space is  , and states correspond to maximal consistent subsets of
, and states correspond to maximal consistent subsets of 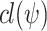 , possibly in the scope of an existential quantifier of O. Accordingly, the product can be minimized to include only consistent pairs. Also, since traditional-synthesis algorithms, in particular the Safraless algorithms we use, can handle automata with generalized Büchi and co-Büchi acceptance condition, we need only one copy of the product.
, possibly in the scope of an existential quantifier of O. Accordingly, the product can be minimized to include only consistent pairs. Also, since traditional-synthesis algorithms, in particular the Safraless algorithms we use, can handle automata with generalized Büchi and co-Büchi acceptance condition, we need only one copy of the product. 
Remark 2
[Determinancy of the
ge-synthesis game]. Determinancy of games implies that in traditional synthesis, a specification 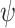 is not I/O-realizable iff
is not I/O-realizable iff  is O/I-realizable This is useful, for example when we want to synthesize a transducer of a bounded size and proceed simultaneously, aiming to synthesize either a system transducer that realizes
is O/I-realizable This is useful, for example when we want to synthesize a transducer of a bounded size and proceed simultaneously, aiming to synthesize either a system transducer that realizes 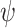 or an environment transducer that realizes
or an environment transducer that realizes  [17]. For ge-synthesis, simple dualization does not hold, but we do have determinancy in the sense that
[17]. For ge-synthesis, simple dualization does not hold, but we do have determinancy in the sense that  is not I/O-realizable iff
is not I/O-realizable iff  is O/I-realizable. Accordingly,
is O/I-realizable. Accordingly,  is not ge-realizable iff the environment has a strategy that generates, for each output sequence
is not ge-realizable iff the environment has a strategy that generates, for each output sequence  , a helpful input sequence
, a helpful input sequence  such that
such that 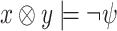 . In the full version, we formalize and study this duality further.
. In the full version, we formalize and study this duality further. 
Guarantees in Good-Enough Synthesis
A drawback of ge-synthesis is that we do not actually know whether the specification is satisfied. In this section we describe two ways to address this drawback. The first way goes beyond providing satisfaction information and enables the designer to partition the specification into to a strong component, which should be satisfied in all environments, and a weak component, which should be satisfied only in hopeful ones. The second way augments ge-realizing transducers by flags, raised to indicate the status of the satisfaction.
ge-Synthesis with a Guarantee
Recall that ge-realizability is suitable especially in settings where we design a system that has to do its best in all environments. ge-synthesis with a guarantee is suitable in settings where we want to make sure that some components of the specification are satisfied in all environment. Accordingly, a specification is an LTL formula  . When we ge
-synthesize
. When we ge
-synthesize
 with guarantee
with guarantee
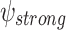 , we seek a transducer
, we seek a transducer  that realizes
that realizes  and ge-realizes
and ge-realizes  . Thus, for all input sequences
. Thus, for all input sequences  , we have that
, we have that  , and if x is hopeful for
, and if x is hopeful for  , then
, then 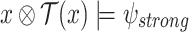 .
.
Theorem 2
The LTL ge-synthesis with guarantee problem is 2EXPTIME-complete.
Proof
Consider an LTL formula 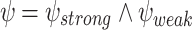 over
over 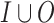 . It is not hard to see that a transducer
. It is not hard to see that a transducer  ge-realizes
ge-realizes  with guarantee
with guarantee  iff
iff  realizes
realizes 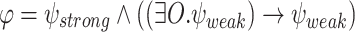 . We can then construct a UCW
. We can then construct a UCW 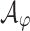 for
for 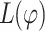 by dualizing an NBW for its negation
by dualizing an NBW for its negation  , which can be constructed using techniques similar to those in the proof of Theorem 1. We then proceed with standard synthesis for
, which can be constructed using techniques similar to those in the proof of Theorem 1. We then proceed with standard synthesis for 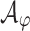 . Note that the approach is Safraless. Taking an empty (that is,
. Note that the approach is Safraless. Taking an empty (that is,  ) guarantee, a lower bound follows from the 2EXPTIME-hardness of LTL ge-synthesis.
) guarantee, a lower bound follows from the 2EXPTIME-hardness of LTL ge-synthesis. 
Flags by a ge-Realizing Transducer
For a language 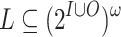 and a finite word
and a finite word  , let
, let  . That is,
. That is,  is the language of suffixes of words in L that have w as a prefix. We say that a word
is the language of suffixes of words in L that have w as a prefix. We say that a word 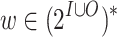 is green for
L if
is green for
L if  is realizable. Then, a word
is realizable. Then, a word  is green for
L if there is
is green for
L if there is 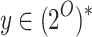 such that
such that  is green for L. When a system is lucky to interact with an environment that generates a green input sequence, we want the system to react in a way that generates a green prefix, and then realizes the specification. Formally, we say that a strategy
is green for L. When a system is lucky to interact with an environment that generates a green input sequence, we want the system to react in a way that generates a green prefix, and then realizes the specification. Formally, we say that a strategy  green realizes
L if for every
green realizes
L if for every  , if x is green for L, then
, if x is green for L, then 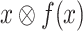 is green for L.1
is green for L.1 2 We say that a word
2 We say that a word  is light green for
L if
is light green for
L if  is universally satisfiable, thus all input sequences are hopeful for
is universally satisfiable, thus all input sequences are hopeful for  . A word
. A word 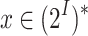 is light green for
L if there is
is light green for
L if there is 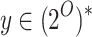 such that
such that 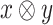 is light green for L. It is not hard to see that for ge-realizable languages, green and light green coincide. Indeed, if L is universally satisfiable and ge-realizable, then L is realizable.
is light green for L. It is not hard to see that for ge-realizable languages, green and light green coincide. Indeed, if L is universally satisfiable and ge-realizable, then L is realizable.
Theorem 3
ge-realizability is strictly stronger than green realizability.
Proof
We first prove that every strategy  that ge-realizes a specification
that ge-realizes a specification 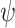 also green realizes
also green realizes  . Consider
. Consider  that is green for
that is green for 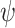 . By definition, there is
. By definition, there is  such that
such that 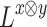 is realizable. Then, for every
is realizable. Then, for every 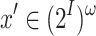 , there is
, there is 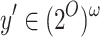 such that
such that  in
in 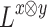 . Hence, for every
. Hence, for every 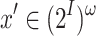 , we have that
, we have that  is hopeful. Therefore, as f
ge-realizes
is hopeful. Therefore, as f
ge-realizes 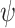 , we have that
, we have that 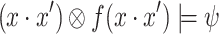 . Thus,
. Thus, 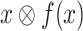 is green, and so f green realizes
is green, and so f green realizes 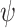 .
.
We continue and describe a specification that is green realizable and not ge-realizable. Let 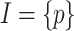 and
and 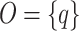 . Consider the specification
. Consider the specification  . Clearly,
. Clearly, 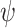 is not realizable, as the system has to commit a value for q before a value for Xp is known. Likewise, no word
is not realizable, as the system has to commit a value for q before a value for Xp is known. Likewise, no word  is green for
is green for  , and so no finite input sequence
, and so no finite input sequence 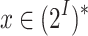 is green for
is green for 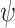 . Hence, every strategy (vacuously) green realizes
. Hence, every strategy (vacuously) green realizes  . On the other hand, for every input sequences
. On the other hand, for every input sequences  there is an output sequence
there is an output sequence  such that
such that 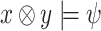 . Thus, all input sequences are hopeful for
. Thus, all input sequences are hopeful for 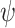 . Thus, synthesis and ge-synthesis coincide for
. Thus, synthesis and ge-synthesis coincide for 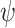 , which is not ge-realizable.
, which is not ge-realizable. 
Theorem 3 brings with it two good news. The first is that a ge-realizing transducer has the desired property of being also green realizing. The second has to do with our goal of providing the user with information about the satisfaction status, in particular raising a green flag whenever a green prefix is detected. By Theorem 3, such a flag indicates that the computation generated by our ge-realizing transducer satisfies the specification. A naive way to detect green prefixes for a specification 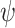 is to solve the synthesis problem for
is to solve the synthesis problem for 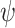 by solving a game on top of a DPW
by solving a game on top of a DPW  for
for 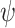 . The winning positions in the game are states in
. The winning positions in the game are states in  . By defining them as accepting states, we can obtain from
. By defining them as accepting states, we can obtain from  a DFW for green prefixes. Then, we run this DFW in parallel with the ge-realizing transducer, and raise the green flag whenever a green prefix is detected. This, however, requires a generation of
a DFW for green prefixes. Then, we run this DFW in parallel with the ge-realizing transducer, and raise the green flag whenever a green prefix is detected. This, however, requires a generation of  and a solution of parity games. Below we describe a much simpler way, which makes use of the fact that our transducer ge-realizes the specification.
and a solution of parity games. Below we describe a much simpler way, which makes use of the fact that our transducer ge-realizes the specification.
Recall that if L is universally satisfiable and ge-realizable, then L is realizable. Accordingly, given a transducer  that ge-realizes
that ge-realizes 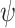 , we can augment it with green flags by running in parallel a DFW that detects light-green prefixes. As we argue below, constructing such a DFW only requires an application of the subset construction on top of an NBW for the existential projection of
, we can augment it with green flags by running in parallel a DFW that detects light-green prefixes. As we argue below, constructing such a DFW only requires an application of the subset construction on top of an NBW for the existential projection of 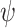 on
on  .
.
Lemma 1
Given an LTL formula 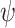 over
over  , we can construct a DFA
, we can construct a DFA 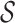 of size
of size  such that
such that  .
.
Proof
Let 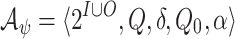 be an NBW for
be an NBW for  , and let
, and let  ,
,  ,
,  be its existential projection on
be its existential projection on  . Thus, for every
. Thus, for every  and
and 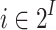 , we have
, we have  . We define the DFW
. We define the DFW  , where M follows the subset construction of
, where M follows the subset construction of  : for every
: for every  and
and 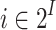 , we have
, we have  . Then,
. Then,  . Observe that
. Observe that  rejects
rejects 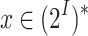 iff there is
iff there is 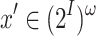 such that for all
such that for all 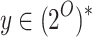 and
and 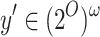 , no state in
, no state in  accepts
accepts 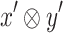 . Thus,
. Thus,  rejects x iff x is not light green, and accepts it otherwise. Note that the definition of F involves universality checking, possibly via complementation, yet no determinization is required, and the size of
rejects x iff x is not light green, and accepts it otherwise. Note that the definition of F involves universality checking, possibly via complementation, yet no determinization is required, and the size of  is
is  .
. 
Note that once we reach an accepting state in  , we can make it an accepting loop. Indeed, once a green prefix is detected, then all prefixes that extend it are green. Accordingly, once the green flag is raised, it stays up. Also note that if an input sequence is not hopeful for
, we can make it an accepting loop. Indeed, once a green prefix is detected, then all prefixes that extend it are green. Accordingly, once the green flag is raised, it stays up. Also note that if an input sequence is not hopeful for  , then none of its prefixes is light green for
, then none of its prefixes is light green for 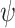 . The converse, however, is not true: an input sequence may be hopeful and still have no light green prefixes. For example, taking
. The converse, however, is not true: an input sequence may be hopeful and still have no light green prefixes. For example, taking 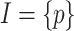 , the input sequence
, the input sequence  is hopeful for
is hopeful for  , yet none of its prefixes is green light, as it can be extended to an input sequence with
, yet none of its prefixes is green light, as it can be extended to an input sequence with  .
.
Green flags provide information about satisfaction. Two additional flags of interest are related to safety and co-safety properties:
A word
 is red for
L if
is red for
L if 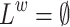 . A word
. A word 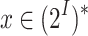 is red for
L if for all
is red for
L if for all  , we have that
, we have that  is red for L. Thus, when the environment generates x, then no matter how the system responds, L is not satisfied.
is red for L. Thus, when the environment generates x, then no matter how the system responds, L is not satisfied.a word
 is blue for
L when
is blue for
L when  , and then define a word
, and then define a word 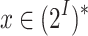 as blue for
L if there is
as blue for
L if there is 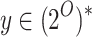 such that
such that  is blue for L. Thus, when the environment generates x, the system can respond in a way that guarantees satisfaction no matter how the interaction continues.
is blue for L. Thus, when the environment generates x, the system can respond in a way that guarantees satisfaction no matter how the interaction continues.
A monitor that detects red and blue prefixes for L can be added to a transducer that ge-realizes L. As has been the case with the monitor for green prefixes, its construction is based on applying the subset construction on an NBW for L [16]. Also, once a red or blue flag is raised, it stays up. In a way analogous to green realizability, we seek a transducer that ge-realizes the specification and generates a red prefix only if all interactions generate a red prefix, and generates a blue prefix whenever this is possible. In the full version, we show that while ge-realization implies red realization, it may conflict with blue realization.
High-Quality Good-Enough Synthesis
ge-synthesis is of special interest when the satisfaction value of the specification is multi-valued, and we want to synthesize high-quality systems. We start by defining the multi-valued logic  , which is our multi-valued specification formalism. We then study
, which is our multi-valued specification formalism. We then study  ge-synthesis, first in a worst-case approach, where the satisfaction value of a transducer is the satisfaction value of its computation with the lowest satisfaction value, and then in a stochastic approach, where it is the expected satisfaction value, given a distribution of the inputs.
ge-synthesis, first in a worst-case approach, where the satisfaction value of a transducer is the satisfaction value of its computation with the lowest satisfaction value, and then in a stochastic approach, where it is the expected satisfaction value, given a distribution of the inputs.
The Logic 
Let AP be a set of Boolean atomic propositions and let 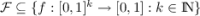 be a set of quality operators. An
be a set of quality operators. An  formula is one of the following:
formula is one of the following:
 ,
, 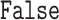 , or p, for
, or p, for  .
. ,
, 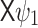 , or
, or 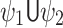 , for
, for  formulas
formulas  and a function
and a function 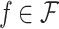 .
.
The semantics of  formulas is defined with respect to infinite computations over AP. For a computation
formulas is defined with respect to infinite computations over AP. For a computation 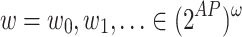 and position
and position 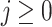 , we use
, we use  to denote the suffix
to denote the suffix  . The semantics maps a computation w and an
. The semantics maps a computation w and an  formula
formula 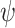 to the satisfaction value of
to the satisfaction value of  in w, denoted
in w, denoted  . The satisfaction value is in [0, 1] and is defined inductively as follows.
. The satisfaction value is in [0, 1] and is defined inductively as follows.
 and
and 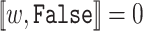 .
.For
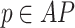 , we have that
, we have that 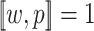 if
if 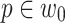 , and
, and  if
if  .
. .
. .
. .
.
The logic  can be viewed as
can be viewed as  for
for  that models the usual Boolean operators. In particular, the only possible satisfaction values are 0 and 1. We abbreviate common functions as described below. Let
that models the usual Boolean operators. In particular, the only possible satisfaction values are 0 and 1. We abbreviate common functions as described below. Let  . Then,
. Then,![]()
The realizability problem for  is an optimization problem: For an
is an optimization problem: For an  specification
specification 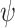 and a transducer
and a transducer  , we define the satisfaction value of
, we define the satisfaction value of 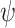 in
in  , denoted
, denoted 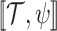 , by
, by 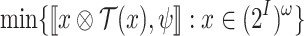 , namely the satisfaction value of
, namely the satisfaction value of  in the worst-case. Then, the synthesis problem is to find, given
in the worst-case. Then, the synthesis problem is to find, given 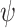 , a transducer that maximizes its satisfaction value. Moving to a decision problem, given
, a transducer that maximizes its satisfaction value. Moving to a decision problem, given 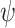 and a threshold value
and a threshold value  , we say that
, we say that 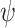 is v-realizable if there exists a transducer
is v-realizable if there exists a transducer  such that
such that  , and the synthesis problem is to find, given
, and the synthesis problem is to find, given  and v, a transducer
and v, a transducer  that v-realizes
that v-realizes 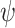 .
.
For an  formula
formula 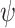 , let
, let  be the set of possible satisfaction values of
be the set of possible satisfaction values of 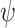 in arbitrary computations. Thus,
in arbitrary computations. Thus, 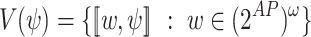 .
.
Theorem 4
[1]. Consider an  formula
formula 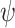 .
.
 .
.For every predicate
 , there exists an NBW
, there exists an NBW  such that
such that  . Furthermore,
. Furthermore,  has at most
has at most 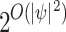 states
[1].
states
[1].
As with LTL, we define the existential and universal extensions  and
and  of
of  . Here too, we consider the case
. Here too, we consider the case 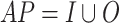 , with the signals in O being quantified. Then,
, with the signals in O being quantified. Then, 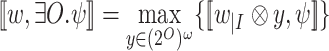 and
and  .
.
Remark 3
[On the semantics of
 ]. It is tempting to interpret an expression like
]. It is tempting to interpret an expression like 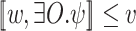 as “there exists an output sequence y such that
as “there exists an output sequence y such that 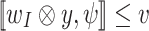 ”. By the semantics of
”. By the semantics of  , however,
, however, 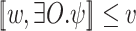 actually means that
actually means that  . Thus, the correct interpretation is “for all output sequences y, we have that
. Thus, the correct interpretation is “for all output sequences y, we have that  ”.
”. 
 ge-Synthesis
ge-Synthesis
For a value  , we say that x is v-hopeful for
, we say that x is v-hopeful for
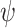 if there is
if there is  such that
such that  . We study two variants of
. We study two variants of  ge-synthesis:
ge-synthesis:
In
 ge
-synthesis with a threshold, the input is an
ge
-synthesis with a threshold, the input is an  formula
formula  and a value
and a value 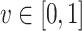 , and the goal is to generate a transducer whose computation on every input sequence that is v-hopeful has satisfaction value at least v. Formally, a function
, and the goal is to generate a transducer whose computation on every input sequence that is v-hopeful has satisfaction value at least v. Formally, a function 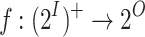 ge-realizes
ge-realizes  with threshold v if for every
with threshold v if for every  , if x is v-hopeful, then
, if x is v-hopeful, then 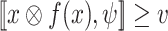 .
.In
 ge
-synthesis, the input is an
ge
-synthesis, the input is an  formula
formula 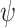 , and the goal is to generate a transducer whose computation on every input sequence has the highest possible satisfaction value for this input sequence. Formally, a function
, and the goal is to generate a transducer whose computation on every input sequence has the highest possible satisfaction value for this input sequence. Formally, a function 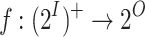 ge-realizes
ge-realizes 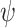 if for every
if for every  and value
and value 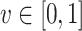 , if x is v-hopeful, then
, if x is v-hopeful, then 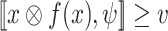 .
.
In the Boolean case, the two variants coincide, taking  . Indeed, then, for every
. Indeed, then, for every  , if x is hopeful, then
, if x is hopeful, then 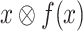 has to satisfy
has to satisfy 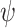 . We note that ge-realization with a threshold is not monotone, in the sense that decreasing the threshold need not lead to ge-realization. Indeed, the lower is the threshold v, the more input sequences are v-helpful (see Example 2). Accordingly, we do not search for a maximal threshold, and rather may ask about a desired threshold or about ge-synthesis without a threshold.
. We note that ge-realization with a threshold is not monotone, in the sense that decreasing the threshold need not lead to ge-realization. Indeed, the lower is the threshold v, the more input sequences are v-helpful (see Example 2). Accordingly, we do not search for a maximal threshold, and rather may ask about a desired threshold or about ge-synthesis without a threshold.
Solving the ge-synthesis problem, a naive combination of the automata construction of Theorem 4 with the projection technique of Theorem 1, corresponds to an erroneous semantics of  , as noted in Remark 3. Before describing our construction, it is helpful to state the correct (perhaps less intuitive) interpretation of existential and universal quantification in the quantitative setting:
, as noted in Remark 3. Before describing our construction, it is helpful to state the correct (perhaps less intuitive) interpretation of existential and universal quantification in the quantitative setting:
Lemma 2
For every  formula
formula 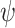 and an input sequence
and an input sequence  , we have that
, we have that 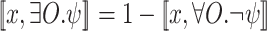 . Accordingly, for every value
. Accordingly, for every value  , we have that
, we have that  iff
iff 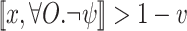 .
.
Proof
By definition,  . Then,
. Then, 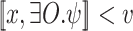 iff
iff 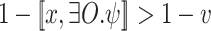 iff
iff  .
. 
Consider an  formula
formula 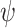 , a value
, a value  , and an input sequence
, and an input sequence  . Recall that x is v-hopeful for
. Recall that x is v-hopeful for 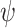 if there is
if there is  such that
such that  . Equivalently,
. Equivalently,  . Indeed,
. Indeed, 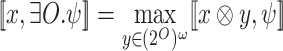 , which is greater or equal to v iff there is
, which is greater or equal to v iff there is  such that
such that  . Hence, x is not v-hopeful for
. Hence, x is not v-hopeful for  if
if  . Equivalently, by Lemma 2,
. Equivalently, by Lemma 2,  . Accordingly, for a strategy
. Accordingly, for a strategy  , an input sequence
, an input sequence  , and a value
, and a value  , we say that f is v-good for
x
with respect to
, we say that f is v-good for
x
with respect to
 , if
, if 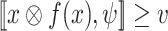 or
or  .
.
Example 2
Let 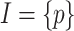 and
and 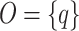 . Consider the
. Consider the  formula
formula  . Checking for which values v a strategy f is v-good for x with respect to
. Checking for which values v a strategy f is v-good for x with respect to 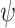 , we examine whether
, we examine whether  or
or 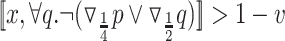 . Since
. Since 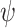 refers only to the first position in the computation, it is enough to examine
refers only to the first position in the computation, it is enough to examine  and
and  . For example, if
. For example, if 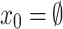 and
and 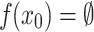 , then
, then  ,
,  , and
, and 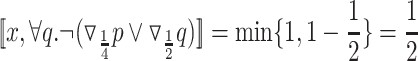 . Hence, f is v-good for x with respect to
. Hence, f is v-good for x with respect to 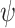 if
if 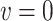 or
or 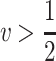 , thus
, thus  . Similarly, we have the following.
. Similarly, we have the following.
If
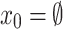 and
and  then f is v-good for x when
then f is v-good for x when  .
.If
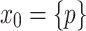 and
and 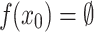 then f is v-good for x when
then f is v-good for x when  .
.If
 and
and then f is v-good for x when
then f is v-good for x when  .
.
Theorem 5
The  ge-synthesis with threshold problem is 2EXPTIME-complete.
ge-synthesis with threshold problem is 2EXPTIME-complete.
Proof
We show we can adjust the upper bound described in the proof of Theorem 1 to the multi-valued setting. Given an  formula
formula 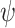 over
over 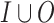 and a threshold
and a threshold  , we describe an algorithm that returns a transducer
, we describe an algorithm that returns a transducer  that ge-realizes
that ge-realizes 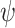 with threshold v, or declares that no such transducer exists.
with threshold v, or declares that no such transducer exists.
By definition, we have that  ge-realizes
ge-realizes 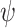 with threshold v if for every input sequence x, we have that
with threshold v if for every input sequence x, we have that  is v-good for x with respect to
is v-good for x with respect to 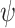 . Thus,
. Thus,  or
or 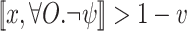 . We construct a UCW whose language is
. We construct a UCW whose language is  .
.
Let  be an NBW for
be an NBW for 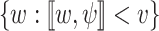 and
and 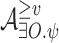 be an NBW for
be an NBW for  . Thus,
. Thus, 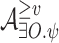 is obtained from an NBW
is obtained from an NBW  for
for 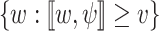 by existentially projecting its transitions on
by existentially projecting its transitions on  . By Theorem 4, both
. By Theorem 4, both 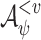 and
and 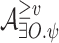 are of size exponential in
are of size exponential in  .
.
Let  be an NBW for the intersection of
be an NBW for the intersection of 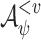 and
and  . The language of
. The language of 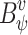 is then
is then 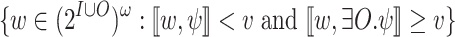 . We then solve usual synthesis for the complementing UCW, whose language is
. We then solve usual synthesis for the complementing UCW, whose language is 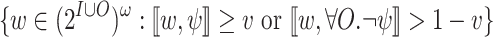 , as required. By
[17], the synthesis problem for UCW can be solved in EXPTIME.
, as required. By
[17], the synthesis problem for UCW can be solved in EXPTIME.
The lower bound follows from the 2EXPTIME-hardness of LTL ge-realizability. 
Theorem 6
The  ge-synthesis problem is 2EXPTIME-complete.
ge-synthesis problem is 2EXPTIME-complete.
Proof
We start with the upper bound. Given an  specification
specification 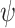 over
over  , we describe an algorithm that returns a transducer
, we describe an algorithm that returns a transducer  that ge-realizes
that ge-realizes  or declares that no such transducer exists.
or declares that no such transducer exists.
As discussed above, a transducer  ge-realizes
ge-realizes  iff for every input sequence
iff for every input sequence  and value
and value  , we have that
, we have that  is v-good for x with respect to
is v-good for x with respect to 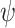 . Accordingly, we construct a UCW whose language is
. Accordingly, we construct a UCW whose language is  .
.
For  , let
, let 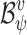 be an NBW for
be an NBW for  , as constructed in the proof of Theorem 5, and let
, as constructed in the proof of Theorem 5, and let 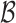 be the union of
be the union of  for all
for all 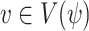 . By Theorem 4, the size of
. By Theorem 4, the size of  is exponential in
is exponential in 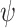 , and thus so is the size of
, and thus so is the size of 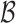 . We then solve usual synthesis for the complementing UCW, whose language is as required. By
[17], the synthesis problem for UCW can be solved in EXPTIME. The lower bound follows from the 2EXPTIME-hardness of LTL ge-realizability.
. We then solve usual synthesis for the complementing UCW, whose language is as required. By
[17], the synthesis problem for UCW can be solved in EXPTIME. The lower bound follows from the 2EXPTIME-hardness of LTL ge-realizability. 
Remark 4
[Tuning hope down]. The quantitative setting allows the designer to tune down “satisfaction by hoplessness”: rather than synthesizing  , we can have a factor
, we can have a factor 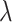 and synthesize
and synthesize 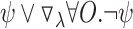 . In Sect. 5.3 below we study additional ways to refer to hopefulness levels.
. In Sect. 5.3 below we study additional ways to refer to hopefulness levels.
 Assume-Guarantee ge-Synthesis
Assume-Guarantee ge-Synthesis
In Sect. 5.2, we seek a transducer  such that for a given or for all values
such that for a given or for all values  and input sequences
and input sequences  , if
, if  then
then 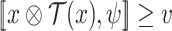 . In this section we measure the quality of a transducer
. In this section we measure the quality of a transducer  by analyzing richer relations between
by analyzing richer relations between  and
and  . The setting has the flavor of quantitative assume-guarantee synthesis
[3]. There, the specification consists of a multi-valued assumption A, which in our case is
. The setting has the flavor of quantitative assume-guarantee synthesis
[3]. There, the specification consists of a multi-valued assumption A, which in our case is  , and a multi-valued guarantee G, which is our case is
, and a multi-valued guarantee G, which is our case is 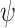 .
.
There are different ways to analyze the relation between  and
and  . To this end, we assume that we are given a function
. To this end, we assume that we are given a function  that given the satisfaction values of
that given the satisfaction values of 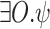 and of
and of 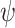 , outputs a combined satisfaction value. We assume that
, outputs a combined satisfaction value. We assume that  is decreasing in the first component and increasing in the second component. This corresponds to the intuition that a lower satisfaction value of
is decreasing in the first component and increasing in the second component. This corresponds to the intuition that a lower satisfaction value of 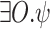 and a higher satisfaction value of
and a higher satisfaction value of  both yield a higher overall score. Also, since
both yield a higher overall score. Also, since  for all
for all  , we assume that the first component is greater than or equal to the second. Finally, we require
, we assume that the first component is greater than or equal to the second. Finally, we require  to be efficiently computed. Some natural
to be efficiently computed. Some natural  functions include:
functions include:
The quantitative implication function:
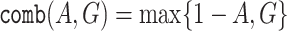 . This captures the quantitative notion of the implication
. This captures the quantitative notion of the implication  .
.The (negated) difference function:
 . This captures how far the satisfaction value for the given computation is from the best satisfaction value. Since
. This captures how far the satisfaction value for the given computation is from the best satisfaction value. Since 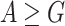 , the range of the function is indeed [0, 1].
, the range of the function is indeed [0, 1].The ratio function, given by some normalization to [0, 1] of the function
 , which captures the “relative success” with respect to the best possible satisfaction value.
, which captures the “relative success” with respect to the best possible satisfaction value.
The choice of an appropriate 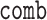 function depends on the setting. Implication is in order when harsh environments may outweigh the actual performance of the system. For example, if our specification measures the uptime of a server in a cluster, then environments that cause very frequent power failures render the server unusable, as the overhead of reconnecting it outweighs its usefulness. In such a case, being shut down is better than continuously trying to reconnect, and so we give a higher satisfaction value for the server being down, which depends only on the environment. Then, as demonstrated with the cleaning robot in Sect. 1, the difference and ratio functions are fairly natural when measuring “realization of potential”. We now describe a more detailed example when these measures are in order.
function depends on the setting. Implication is in order when harsh environments may outweigh the actual performance of the system. For example, if our specification measures the uptime of a server in a cluster, then environments that cause very frequent power failures render the server unusable, as the overhead of reconnecting it outweighs its usefulness. In such a case, being shut down is better than continuously trying to reconnect, and so we give a higher satisfaction value for the server being down, which depends only on the environment. Then, as demonstrated with the cleaning robot in Sect. 1, the difference and ratio functions are fairly natural when measuring “realization of potential”. We now describe a more detailed example when these measures are in order.
Example 3
Consider a controller for an elevator in an n-floor building. The environment sends to the controller requests, by means of a truth assignment to  , indicating the subset of floors in which the elevator is requested. Then, the controller assigns values to
, indicating the subset of floors in which the elevator is requested. Then, the controller assigns values to 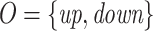 , directing the elevator to go up, go down, or stay. The satisfaction value of the specification
, directing the elevator to go up, go down, or stay. The satisfaction value of the specification 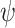 reflects the waiting time of the request with the slowest response: it is 0 when this time is more than 2n, and is 1 when the slowest request is granted immediately. Sure enough, there is no controller that attains satisfaction value 1 on all input sequences, and so
reflects the waiting time of the request with the slowest response: it is 0 when this time is more than 2n, and is 1 when the slowest request is granted immediately. Sure enough, there is no controller that attains satisfaction value 1 on all input sequences, and so 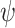 is not realizable with satisfaction value 1. Also, adding assumptions about the behavior of the environment is not of much interest. Using AG ge-realizability, we can synthesize a controller that behaves in an optimal way. For example, using the difference function, we measure the performance of the controller on an input sequence
is not realizable with satisfaction value 1. Also, adding assumptions about the behavior of the environment is not of much interest. Using AG ge-realizability, we can synthesize a controller that behaves in an optimal way. For example, using the difference function, we measure the performance of the controller on an input sequence  with respect to the best possible performance on x. Note that such a best performance needs a look-ahead on requests yet to come, which is indeed the satisfaction value of
with respect to the best possible performance on x. Note that such a best performance needs a look-ahead on requests yet to come, which is indeed the satisfaction value of  in x. Thus, the assumption
in x. Thus, the assumption  actually gives us the performance of a good-enough off-line controller. Accordingly, using the ratio function, we can synthesize a system with the best competitive ratio for an on-line interaction
[7].
actually gives us the performance of a good-enough off-line controller. Accordingly, using the ratio function, we can synthesize a system with the best competitive ratio for an on-line interaction
[7]. 
Given an  formula
formula 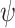 and a function
and a function  , we define the ge
-AG-realization value of
, we define the ge
-AG-realization value of 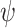 in a transducer
in a transducer  by
by 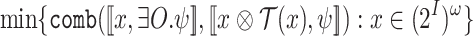 . Then, our goal in AG
ge
-realizability is to find, given an
. Then, our goal in AG
ge
-realizability is to find, given an  formula
formula 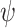 and a function
and a function  , the maximal value
, the maximal value  such that there exists a transducer
such that there exists a transducer  whose AG ge-realization value of
whose AG ge-realization value of 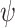 is v. The AG
ge
-synthesis problem is then to find such a transducer.
is v. The AG
ge
-synthesis problem is then to find such a transducer.
We start by solving the decision version of AG ge-realizability.
Theorem 7
The problem of deciding, given an  formula
formula  , a function
, a function  , and a threshold
, and a threshold  , whether there exists a transducer
, whether there exists a transducer  whose AG ge-realization value of
whose AG ge-realization value of 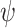 is v, is 2EXPTIME-complete.
is v, is 2EXPTIME-complete.
Proof
Recall that  is the set of possible satisfaction values of
is the set of possible satisfaction values of  (and hence of
(and hence of 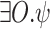 ), and that by Theorem 4, we have that
), and that by Theorem 4, we have that 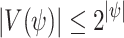 . Let
. Let  . Intuitively, G is the set of satisfaction-value pairs
. Intuitively, G is the set of satisfaction-value pairs  that are allowed to be generated by a transducer whose AG ge-realization value of
that are allowed to be generated by a transducer whose AG ge-realization value of  is at least v. By definition, AG ge-realization of
is at least v. By definition, AG ge-realization of  with value v coincides with realization of the language
with value v coincides with realization of the language  . By the monotonicity assumption on
. By the monotonicity assumption on  , for every
, for every  , we have that
, we have that  for every
for every  and
and  . Hence, we can write
. Hence, we can write  , and proceed to construct an NBW for
, and proceed to construct an NBW for  by taking the union of NBWs
by taking the union of NBWs 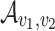 for all
for all  , each of which is the product of NBWs
, each of which is the product of NBWs 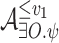 and
and 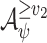 , as in the proof of Theorem 5.
, as in the proof of Theorem 5.
Aiming to proceed Safralessly, we can also construct a UCW for  , as follows. First, note that by the monotonicity of
, as follows. First, note that by the monotonicity of  , for every
, for every  we have that
we have that  iff for every
iff for every  , we have that
, we have that  or
or  . Hence,
. Hence,  , and so by dualization we have
, and so by dualization we have  . Hence, we can obtain a UCW for
. Hence, we can obtain a UCW for  by dualizing an NBW that is the union of NBWs
by dualizing an NBW that is the union of NBWs 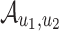 , for all
, for all  , each of which is the product of NBWs
, each of which is the product of NBWs 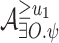 and
and 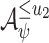 .
.
Observe that in all cases, the size of the NBW is  . Indeed, there are at most
. Indeed, there are at most 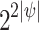 pairs in the union, and, by Theorem 4, the size of the NBW for each pair is
pairs in the union, and, by Theorem 4, the size of the NBW for each pair is  .
.
The lower bound follows from the 2EXPTIME-hardness of LTL ge-realizability. 
By Theorem 4, the number of possible satisfaction values for 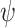 is at most
is at most 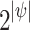 . Thus, the number of possible values for
. Thus, the number of possible values for 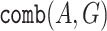 , where A and G are satisfaction values of
, where A and G are satisfaction values of 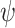 , is at most
, is at most 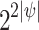 . Using binary search over the image of
. Using binary search over the image of  , we can use Theorem 7 to obtain the following.
, we can use Theorem 7 to obtain the following.
Corollary 1
The AG ge-synthesis problem can be solved in doubly-exponential time.
Remark 5
[
ge-synthesis as a special case of AG
ge-synthesis]. The two approaches taken in Sect. 5.2 can be captured by an appropriate  function. Indeed, for ge-synthesis with a threshold, we can use the function
function. Indeed, for ge-synthesis with a threshold, we can use the function  with
with  if
if 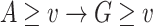 , and
, and 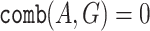 otherwise. For ge-synthesis (without a threshold), we can use the function
otherwise. For ge-synthesis (without a threshold), we can use the function  with
with  if
if  , and
, and  otherwise (recall that
otherwise (recall that 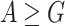 by definition). However, the solution described in Sect. 5.2 is simpler than the one described here for the general case.
by definition). However, the solution described in Sect. 5.2 is simpler than the one described here for the general case. 
 ge-Synthesis in Stochastic Environments
ge-Synthesis in Stochastic Environments
The setting of  ge-synthesis studied in Sects. 5.2 and 5.3 takes the different satisfaction values into an account, but is binary, in the sense that a specification is either (possibly AG) ge-realizable, or is not. In particular, in case the specification is not ge-realizable, synthesis algorithms only return “no”. In this section we add a quantitative measure also to the underlying realizability question. We do so by assuming a stochastic environment, with a known distribution on the inputs sequences, and analyzing the expected performance of the system.
ge-synthesis studied in Sects. 5.2 and 5.3 takes the different satisfaction values into an account, but is binary, in the sense that a specification is either (possibly AG) ge-realizable, or is not. In particular, in case the specification is not ge-realizable, synthesis algorithms only return “no”. In this section we add a quantitative measure also to the underlying realizability question. We do so by assuming a stochastic environment, with a known distribution on the inputs sequences, and analyzing the expected performance of the system.
For completeness, we remind the reader of some basics of probability theory. For a comprehensive reference see e.g.,
[25]. Let  be a finite alphabet, and let
be a finite alphabet, and let  be some probability distribution over
be some probability distribution over  . For example, in the uniform distribution over
. For example, in the uniform distribution over  , the probability space is induced by sampling each letter with probability
, the probability space is induced by sampling each letter with probability 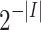 , corresponding to settings in which each signal in I always holds in probability
, corresponding to settings in which each signal in I always holds in probability  . We assume
. We assume  is given by a finite Markov Decision Process (MDP). That is,
is given by a finite Markov Decision Process (MDP). That is,  is induced by the distribution of each letter
is induced by the distribution of each letter 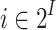 at each time step, determined by a finite stochastic control process that takes into account also the outputs generated by the system (see
[2] for the precise model). A random variable is then a function
at each time step, determined by a finite stochastic control process that takes into account also the outputs generated by the system (see
[2] for the precise model). A random variable is then a function  . When X has a finite image V, which is the case in our setting, its expected value is
. When X has a finite image V, which is the case in our setting, its expected value is 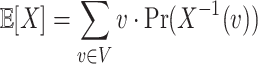 . Intuitively,
. Intuitively,  is the “average” value that X attains. Next, consider an event
is the “average” value that X attains. Next, consider an event
 . The conditional expectation of
X
with respect to
E is
. The conditional expectation of
X
with respect to
E is  , where
, where  is the random variable that assigns X(w) to
is the random variable that assigns X(w) to  and 0 to
and 0 to  . Intuitively,
. Intuitively,  is the average value that X attains when restricting to words in E, and normalizing according to the probability of E itself.
is the average value that X attains when restricting to words in E, and normalizing according to the probability of E itself.
We continue and review the high-quality synthesis problem
[2], where the ge variant is not considered. There, the environment is assumed to be stochastic and we care for the expected satisfaction value of an  specification in the computations of a transducer
specification in the computations of a transducer  , assuming some given distribution on the inputs sequences. Formally, let
, assuming some given distribution on the inputs sequences. Formally, let  be a random variable that assigns each sequence
be a random variable that assigns each sequence  of input signals with
of input signals with  . Then, when the sequences in
. Then, when the sequences in  are sampled according to a given distribution
are sampled according to a given distribution  of
of  , we define
, we define 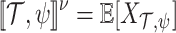 . Since
. Since 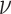 is fixed, we omit it from the notation and use
is fixed, we omit it from the notation and use 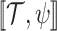 in the following.
in the following.
Remark 6
[Relating LTL
ge-synthesis with stochastic
 synthesis] Given an LTL formula
synthesis] Given an LTL formula 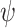 , we can view it as an
, we can view it as an 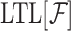 formula with possible satisfaction values
formula with possible satisfaction values 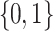 , apply to it high-quality synthesis a-la
[2], and find a transducer
, apply to it high-quality synthesis a-la
[2], and find a transducer  that maximizes
that maximizes  . An interesting observation is that if
. An interesting observation is that if  ge-realizes
ge-realizes  , then it also maximizes
, then it also maximizes  . Indeed, all input sequences that can contribute to the expected satisfaction value, do so.
. Indeed, all input sequences that can contribute to the expected satisfaction value, do so. 
We introduce and study two measures for high-quality synthesis in a stochastic environment. In the first, termed expected ge -synthesis, all input sequences are sampled, yet the satisfaction value in each input sequence takes its hopefulness level into account. In the second, termed conditional expected ge -synthesis, only hopeful input sequences are sampled.
We start with expected ge-synthesis. There, instead of associating each sequence  with
with 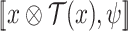 , we associate it with
, we associate it with  , where
, where  is as described in Sect. 5.3, thus capturing the assume-guarantee semantics of quantitative ge-synthesis. Then, we define
is as described in Sect. 5.3, thus capturing the assume-guarantee semantics of quantitative ge-synthesis. Then, we define 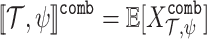 . For example, taking
. For example, taking  as implication, we have
as implication, we have  , capturing the semantics of
, capturing the semantics of  .
.
Then, in conditional expected ge-synthesis, we consider 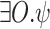 as an environment assumption, and factor it in using conditional expectation, parameterized by a threshold
as an environment assumption, and factor it in using conditional expectation, parameterized by a threshold 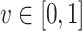 . Formally, let
. Formally, let 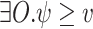 denote the event
denote the event  . Then, we define
. Then, we define  , assuming the event
, assuming the event 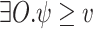 has a strictly positive probability.
has a strictly positive probability.
In
[2], it is shown that the high-quality synthesis problem can be solved in doubly-exponential time, also in the presence of environment assumptions. In the solution, the first step is the translation of the involved formulas to DPWs. In order to extract from
[2] the results relevant to us, we describe them by means of discrete quantitative specifications, defined as follows. A discrete quantitative specification  over
over 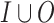 is given by means of a sequence
is given by means of a sequence  of DPWs, with
of DPWs, with 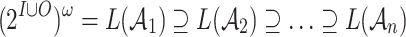 , and sequence
, and sequence  of values. For every
of values. For every 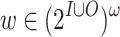 , the satisfaction value of w in
, the satisfaction value of w in 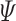 , denoted
, denoted 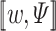 , is
, is 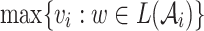 . We refer to n as the depth of
. We refer to n as the depth of  .
.
Theorem 8
(
[2]). Consider a discrete quantitative specification  over
over  . Let n be its depth and m be the size of the largest DPW in
. Let n be its depth and m be the size of the largest DPW in 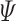 . For a transducer
. For a transducer  , let
, let  be a random variable that assigns a word
be a random variable that assigns a word  with
with 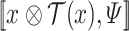 .
.
We can synthesize a transducer
 that maximizes
that maximizes  in time
in time  .
.Given a DPW
 over
over  such that
such that 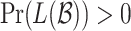 , we can synthesize a transducer
, we can synthesize a transducer  that maximizes
that maximizes  in time
in time  , where k is the size of
, where k is the size of 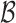 .
.
We can now state the main results of this section.
Theorem 9
Consider an  formula
formula 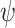 .
.
Given a function
 , we can find in doubly-exponential time a transducer that maximizes
, we can find in doubly-exponential time a transducer that maximizes 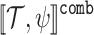 .
.Given a threshold
 , we can find in doubly-exponential time a transducer that maximizes
, we can find in doubly-exponential time a transducer that maximizes 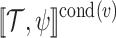 .
.
Proof
Let 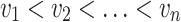 be the possible satisfaction values of
be the possible satisfaction values of  (and hence also of
(and hence also of  and of
and of  ). By Theorem 4, we have that
). By Theorem 4, we have that  . For each
. For each  , we can construct a DPW
, we can construct a DPW 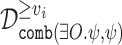 as in Theorem 7. It is not hard to see that the discrete quantitative specification given by the DPWs
as in Theorem 7. It is not hard to see that the discrete quantitative specification given by the DPWs 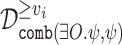 and the values
and the values 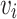 , for
, for  , is qual to the specification
, is qual to the specification 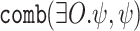 . Thus, by Theorem 8 (1), we can find a transducer that maximizes
. Thus, by Theorem 8 (1), we can find a transducer that maximizes  in time
in time  .
.
Next, given  , we can check whether
, we can check whether 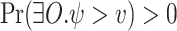 , for example by converting a DPW
, for example by converting a DPW 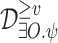 to an MDP, and reasoning about its Ergodic-components. Then, by Theorem 8 (2), we can find a transducer that maximizes
to an MDP, and reasoning about its Ergodic-components. Then, by Theorem 8 (2), we can find a transducer that maximizes 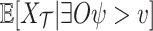 , in time
, in time  .
. 
Corollary 2
The (possibly conditional) expected ge-synthesis problem for  can be solved in doubly-exponential time.
can be solved in doubly-exponential time.
Guarantees in High-Quality ge-Synthesis
As in the Boolean setting, also in the high-quality one we would like to add to a ge-realizing transducer guarantees and indications about the satisfaction level. As we detail below, the quantitative setting offers many possible ways to do so.
High-Quality
ge-Synthesis with Guarantees. We consider specifications of the form 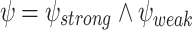 , where essentially, we seek a transducer that realizes
, where essentially, we seek a transducer that realizes  and (possibly AG) ge-realizes
and (possibly AG) ge-realizes  . Maximizing the realization value of
. Maximizing the realization value of 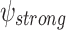 may conflict with maximizing the ge-realization value of
may conflict with maximizing the ge-realization value of 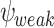 , and there are different ways to trade-off the two goals. Technically, in the decision-problem variant, we are given two thresholds
, and there are different ways to trade-off the two goals. Technically, in the decision-problem variant, we are given two thresholds  , and we seek a transducer
, and we seek a transducer  that realizes
that realizes 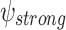 with value at least
with value at least  , and ge-realizes
, and ge-realizes 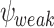 with value at least
with value at least 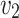 . Then, one may start, for example, by maximizing the value
. Then, one may start, for example, by maximizing the value  , and then find the maximal value
, and then find the maximal value  that may be achieved simultaneously. Alternatively, one may prefer to maximize
that may be achieved simultaneously. Alternatively, one may prefer to maximize 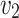 , or some other combination of
, or some other combination of  and
and 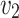 . Also, it is possible to decompose
. Also, it is possible to decompose 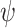 further, to several strong and weak components, each with its desired threshold.
further, to several strong and weak components, each with its desired threshold.
The solutions in the different settings all involve a construction of a UCW 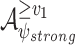 , and its product with the automata constructed in the solutions for the different ge-synthesis variants. We thus have the following. We note that when the solution for
, and its product with the automata constructed in the solutions for the different ge-synthesis variants. We thus have the following. We note that when the solution for  is Safraless, we can use a UCW for
is Safraless, we can use a UCW for  to maintain a Safraless construction.
to maintain a Safraless construction.
Theorem 10
The problem of  high-quality ge-synthesis with a guarantee can be solved in doubly-exponential time.
high-quality ge-synthesis with a guarantee can be solved in doubly-exponential time.
Flags by a High-Quality
ge-Realizing Transducer. In the quantitative setting, we parameterized the flags raised by the ge-realizing transducer by values in [0, 1], indicating the announced satisfaction level. Thus, rather than talking about prefixes being green, red, or blue, we talk about them being v-green, v-red, and v-blue, for 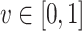 , which essentially means that a satisfaction value of at least v is guarantees (in green and blue flags) or is impossible (in red ones). We can think of those as “degrees” of green, red, and blue. Below, we formalize this intuition and argue that even an augmentation of a transducer that ge-realizes
, which essentially means that a satisfaction value of at least v is guarantees (in green and blue flags) or is impossible (in red ones). We can think of those as “degrees” of green, red, and blue. Below, we formalize this intuition and argue that even an augmentation of a transducer that ge-realizes 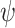 by flags for all values in
by flags for all values in  leaves the problem in doubly-exponential time.
leaves the problem in doubly-exponential time.
A quantitative language over 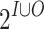 is
is 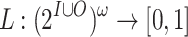 . For a quantitative language L and a word
. For a quantitative language L and a word  , we define
, we define  as the quantitative language where for all
as the quantitative language where for all  , we have
, we have 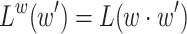 . For a value
. For a value  , a word
, a word  is v-green for
L if
is v-green for
L if  is v-realizable. That is, there is a transducer
is v-realizable. That is, there is a transducer  such that
such that  . A word
. A word 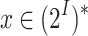 is v-green for
L if there is
is v-green for
L if there is 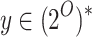 such that
such that  is v-green for L. Thus, when the environment generates x, the system can respond in a way that would guarantee v-realizability. Finally, we say that L is green realizable if there is a strategy
is v-green for L. Thus, when the environment generates x, the system can respond in a way that would guarantee v-realizability. Finally, we say that L is green realizable if there is a strategy 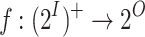 that for every threshold v and for every input
that for every threshold v and for every input  that is v-green for L, we have that
that is v-green for L, we have that  is v-green for L. It is not hard to see that Theorem 3 carries over to the quantitative setting, thus quantitative optimal realizability is strictly stronger than quantitative green realizability. In particular, if a transducer
is v-green for L. It is not hard to see that Theorem 3 carries over to the quantitative setting, thus quantitative optimal realizability is strictly stronger than quantitative green realizability. In particular, if a transducer  optimally realizes an
optimally realizes an  formula
formula  , then
, then  also green realizes
also green realizes  . In the full version, we describe quantitative definitions also for red and blue prefixes, and describe monitors for the detection of the various types of prefixes.
. In the full version, we describe quantitative definitions also for red and blue prefixes, and describe monitors for the detection of the various types of prefixes.
Discussion
We introduced and solved several variants of ge-synthesis. Our complexity results are tight and show that ge-synthesis is not more complex than traditional synthesis. In practice, however, traditional synthesis algorithms do not scale well, and much research is devoted for the development of methods and heuristics for coping with the implementation challenges of synthesis. A natural future research direction is to extend these heuristics and methods for ge-synthesis. We mention here two specific examples.
Efficient synthesis algorithms have been developed for fragments of LTL [21]. Most notable is the GR(1) fragment [18], which supports assume-guarantee reasoning, and for which synthesis has an efficient symbolic solution. Adding existential quantification to GR(1) specifications, which is how we handled LTL ge-synthesis, is not handled by its known algorithms, and is an interesting challenge. The success of SAT-based model-checking have led to the development of SAT-based synthesis algorithms [6], where the synthesis problem is reduced to satisfiability of a QBF formula. The fact the setting already includes quantifiers suggests it can be extended to ge-synthesis. A related effort is bounded synthesis algorithms [13, 24], where the synthesized systems are assumed to be of a bounded size and can be represented symbolically [10].
Footnotes
Note that while the definition of green realization does not refer to  directly, we have that
directly, we have that  is green iff L is realizable, in which case all
is green iff L is realizable, in which case all  are green.
are green.
While synthesis corresponds to finding a winning strategy for the system, green synthesis can be viewed as a subgame-perfect best-response strategy, where the system does its best in every subgame, even if it loses the overall game.
S. Almagor—Supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 837327.
O. Kupferman—Supported in part by the Israel Science Foundation, grant No. 2357/19.
Contributor Information
Shuvendu K. Lahiri, Email: shuvendu.lahiri@microsoft.com
Chao Wang, Email: wang626@usc.edu.
Shaull Almagor, Email: shaull@cs.technion.ac.il.
Orna Kupferman, Email: orna@cs.huji.ac.il.
References
- 1.Almagor S, Boker U, Kupferman O. Formalizing and reasoning about quality. J. ACM. 2016;63(3):24:1–24:56. doi: 10.1145/2875421. [DOI] [Google Scholar]
- 2.Almagor, S., Kupferman, O.: High-quality synthesis against stochastic environments. In: Proceedings of 25th Annual Conference of the European Association for Computer Science Logic, LIPIcs, vol. 62, pp. 28:1–28:17 (2016)
- 3.Almagor S, Kupferman O, Ringert JO, Velner Y. Quantitative assume guarantee synthesis. In: Majumdar R, Kunčak V, editors. Computer Aided Verification; Cham: Springer; 2017. pp. 353–374. [Google Scholar]
- 4.Bloem R, Chatterjee K, Henzinger TA, Jobstmann B. Better quality in synthesis through quantitative objectives. In: Bouajjani A, Maler O, editors. Computer Aided Verification; Heidelberg: Springer; 2009. pp. 140–156. [Google Scholar]
- 5.Bloem R, Chatterjee K, Jobstmann B. Handbook of Model Checking. Cham: Springer; 2018. Graph games and reactive synthesis; pp. 921–962. [Google Scholar]
- 6.Bloem, R., Egly, U., Klampfl, P., Könighofer, R., Lonsing, F.: Sat-based methods for circuit synthesis. In: Proceedings of 14th International Conference on Formal Methods in Computer-Aided Design, pp. 31–34. IEEE (2014)
- 7.Borodin A, El-Yaniv R. Online Computation and Competitive Analysis. New York: Cambridge University Press; 1998. [Google Scholar]
- 8.Chatterjee K, Henzinger TA, Jobstmann B. Environment assumptions for synthesis. In: van Breugel F, Chechik M, editors. CONCUR 2008 - Concurrency Theory; Heidelberg: Springer; 2008. pp. 147–161. [Google Scholar]
- 9.Church, A.: Logic, arithmetics, and automata. In: Proceedings of International Congress of Mathematicians, vol. 1962, pp. 23–35. Institut Mittag-Leffler (1963)
- 10.Ehlers R. Symbolic bounded synthesis. In: Touili T, Cook B, Jackson P, editors. Computer Aided Verification; Heidelberg: Springer; 2010. pp. 365–379. [Google Scholar]
- 11.Fisman D, Kupferman O, Lustig Y. Rational synthesis. In: Esparza J, Majumdar R, editors. Tools and Algorithms for the Construction and Analysis of Systems; Heidelberg: Springer; 2010. pp. 190–204. [Google Scholar]
- 12.Kupferman O. Automata theory and model checking. In: Clarke E, Henzinger T, Veith H, Bloem R, editors. Handbook of Model Checking. Cham: Springer; 2018. pp. 107–151. [Google Scholar]
- 13.Kupferman, O., Lustig, Y., Vardi, M.Y., Yannakakis, M.: Temporal synthesis for bounded systems and environments. In: Proceedings of 28th Symposium on Theoretical Aspects of Computer Science, pp. 615–626 (2011)
- 14.Kupferman O, Perelli G, Vardi MY. Synthesis with rational environments. Ann. Math. Artif. Intell. 2016;78(1):3–20. doi: 10.1007/s10472-016-9508-8. [DOI] [Google Scholar]
- 15.Kupferman O, Piterman N, Vardi MY. Safraless compositional synthesis. In: Ball T, Jones RB, editors. Computer Aided Verification; Heidelberg: Springer; 2006. pp. 31–44. [Google Scholar]
- 16.Kupferman O, Vardi MY. Model checking of safety properties. Formal Methods Syst. Des. 2001;19(3):291–314. doi: 10.1023/A:1011254632723. [DOI] [Google Scholar]
- 17.Kupferman, O., Vardi, M.Y.: Safraless decision procedures. In: Proceedings of 46th IEEE Symposium on Foundations of Computer Science, pp. 531–540 (2005)
- 18.Piterman N, Pnueli A, Sa’ar Y. Synthesis of reactive(1) designs. In: Emerson EA, Namjoshi KS, editors. Verification, Model Checking, and Abstract Interpretation; Heidelberg: Springer; 2005. pp. 364–380. [Google Scholar]
- 19.Pnueli A. The temporal semantics of concurrent programs. Theor. Comput. Sci. 1981;13:45–60. doi: 10.1016/0304-3975(81)90110-9. [DOI] [Google Scholar]
- 20.Pnueli, A., Rosner, R.: On the synthesis of a reactive module. In: Proceedings of 16th ACM Symposium on Principles of Programming Languages, pp. 179–190 (1989)
- 21.Alur R, La Torre S, Madhusudan P. Playing games with boxes and diamonds. In: Amadio R, Lugiez D, editors. CONCUR 2003 - Concurrency Theory; Heidelberg: Springer; 2003. pp. 128–143. [Google Scholar]
- 22.Rosner, R.: Modular synthesis of reactive systems. Ph.D thesis, Weizmann Institute of Science (1992)
-
23.Safra, S.: On the complexity of
 -automata. In: Proceedings of 29th IEEE Symposium on Foundations of Computer Science, pp. 319–327 (1988)
-automata. In: Proceedings of 29th IEEE Symposium on Foundations of Computer Science, pp. 319–327 (1988)
- 24.Schewe S, Finkbeiner B. Bounded synthesis. In: Namjoshi KS, Yoneda T, Higashino T, Okamura Y, editors. Automated Technology for Verification and Analysis; Heidelberg: Springer; 2007. pp. 474–488. [Google Scholar]
- 25.Sheldon R. A First Course in Probability. Delhi: Pearson Education India; 2002. [Google Scholar]
- 26.Sistla AP, Vardi MY, Wolper P. The complementation problem for Büchi automata with applications to temporal logic. Theor. Comput. Sci. 1987;49:217–237. doi: 10.1016/0304-3975(87)90008-9. [DOI] [Google Scholar]
- 27.Vardi MY, Wolper P. Reasoning about infinite computations. Inf. Comput. 1994;115(1):1–37. doi: 10.1006/inco.1994.1092. [DOI] [Google Scholar]
- 28.Winnicott DW. Playing and Reality. Harmondsworth: Penguin; 1971. [Google Scholar]
- 29.Wolper, P.: Temporal logic can be more expressive. In: Proceedings of 22nd IEEE Symposium on Foundations of Computer Science, pp. 340–348 (1981)


