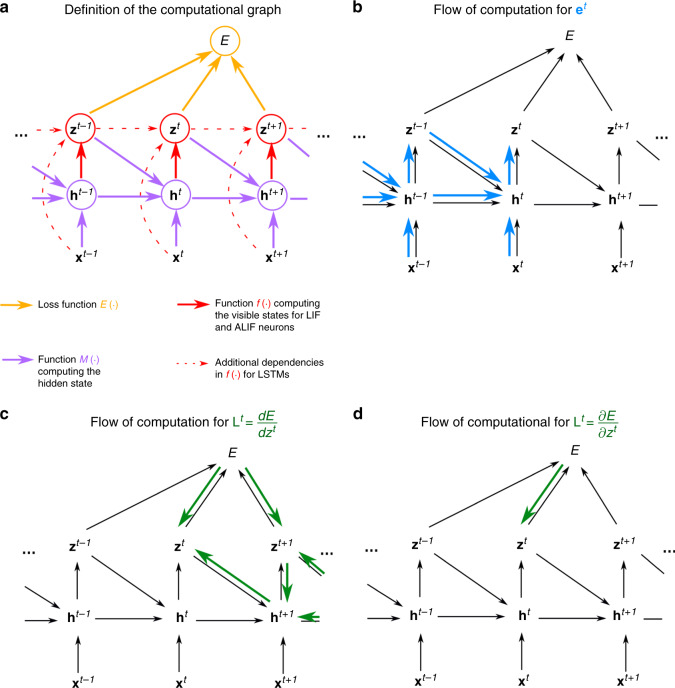
Fig. 6. Computational graph and gradient propagations.

a Assumed mathematical dependencies between hidden neuron states ${\mathbf{h}}_j^t$, neuron outputs z^t, network inputs x^t, and the loss function E through the mathematical functions E( ⋅ ), M( ⋅ ), f( ⋅ ) are represented by colored arrows. b–d The flow of computation for the two components e^t and L^t that merge into the loss gradients of Eq. (3) can be represented in similar graphs. b Following Eq. (14), the flow of the computation of the eligibility traces $e_{ji}^t$ is going forward in time. c Instead, the ideal learning signals $L_j^t=\frac{dE}{d{z}_j^t}$ requires to propagate gradients backward in time. d Hence, while $e_{ji}^t$ is computed exactly, $L_j^t$ is approximated in e-prop applications to yield an online learning algorithm.