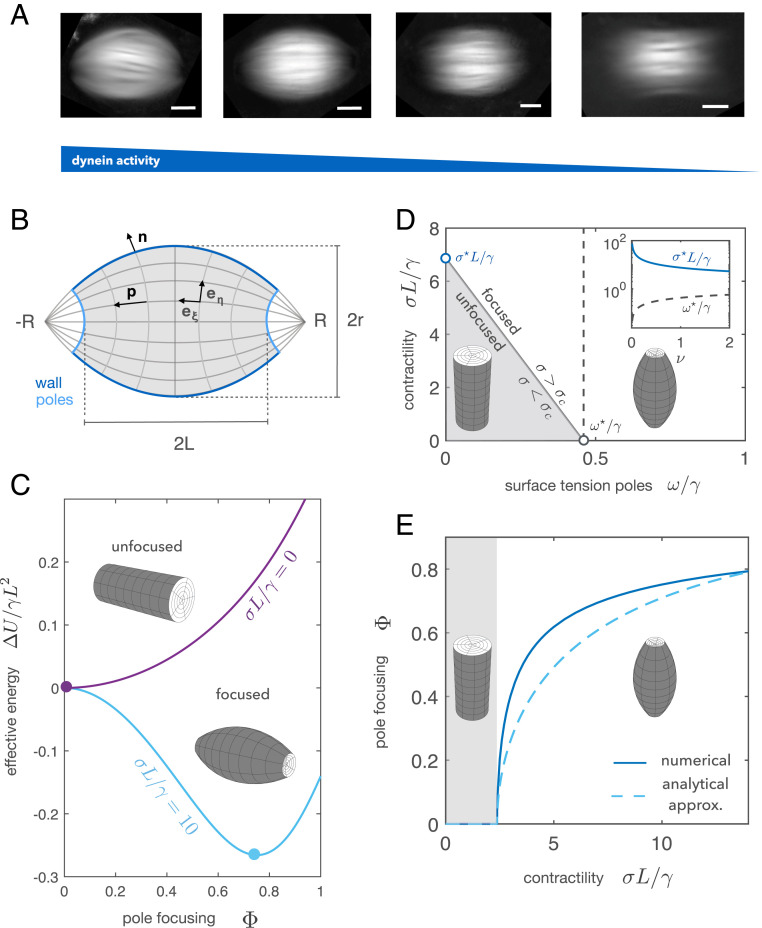
Fig. 1.

Theory of spindle pole focusing. (A) Averaged retardance images of egg extract spindles under different concentrations of the dynein inhibitor p150-CC1. Images correspond to different titration days. (Scale bars: 20 $\mathrm{\mu }$m.) (B) The spindle is described as a tactoid of length $2L$, width $2r$, and pole-to-pole distance $2R$. The two dimensionless parameters describing the spindle shape are the pole focusing parameter $\mathrm{\Phi }=L/R$ and the aspect ratio $a=r/L$. The spindle is parameterized using bispherical coordinates $\left\{\xi ,\eta ,\phi \right\}$, and the director field $\mathbf{p}$ follows the $\xi$ coordinate (SI Appendix). (C) Dimensionless energy of the spindle relative to the cylindrical configuration $\mathrm{\Delta }U/\gamma L^2$ as a function of the pole focusing parameter $\mathrm{\Phi }$ for two different values of the stress $\sigma$. The shape is found by minimizing $\mathrm{\Delta }U=U\left(\mathrm{\Phi }\right)-U\left(0\right)$. (D) Phase diagram of how spindle shape changes as a function of the contractile stress $\sigma$ and the surface tension at the poles $\omega$. (Inset) Evolution of ${\sigma }^{\star }$ and ${\omega }^{\star }$ as a function of the dimensionless volume $\nu$. (E) Bifurcation diagram considering dynein contractility $\sigma$ as the control parameter: Below a certain critical contractility ${\sigma }_c$ the cylindrical configuration $\mathrm{\Phi }=0$ is stable. Once the contractility exceeds the threshold value ${\sigma }_c$, the structure undergoes axisymmetric buckling, acquiring a barrel-like shape. The solid curve corresponds to the full solution, and the dashed curve corresponds to the analytical solution expanding the energy up to quartic order in $\mathrm{\Phi }$ (SI Appendix). The study is done in the limit of constant volume ($AL/\gamma \to \infty$) with parameters $K_1/K_3=1$, $K_1/\gamma L=0.1$, $\omega /\gamma =0.3$, and $\nu =1.2$.