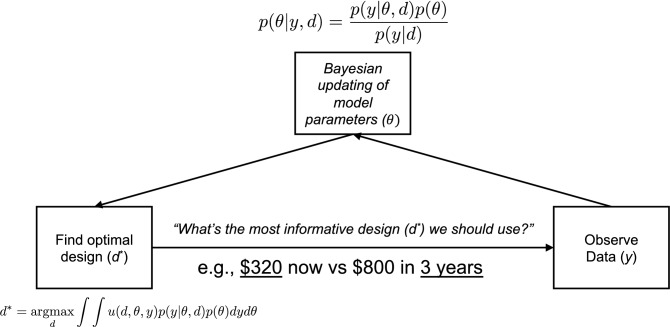
Figure 1.

Schematic illustration of adaptive design optimization (ADO) in the area of delay discounting. Unlike the traditional experimental method, ADO aims to find the optimal design that extracts the maximum information about a participant’s model parameters on each trial. In other words, ADO identifies the most informative or optimal design (d^*) using the participant’s previous choices (y), the mathematical model of choice behavior, and the participant’s model parameters ($\theta$). In our delay discounting experiment with ADO, y would be 0 (choosing smaller and sooner reward) or 1 (larger and later reward), the mathematical model would be the hyperbolic function (see “Methods”), $\theta$ would be k (discounting rate) and $\beta$ (inverse temperature), and d* would be the experimental design (a later delay and a sooner reward, which are underlined in the figure) that maximizes the integral of the local utility function, $u(d,\theta ,y)$, which is based on the mutual information between model parameters ($\theta$) and outcome random variable conditional upon design (y|d). For more mathematical details of the ADO method, see^24,25.