Origin and role of path integration in the cognitive representations of the hippocampus: computational insights into open questions

ABSTRACT

Path integration is a straightforward concept with varied connotations that are important to different disciplines concerned with navigation, such as ethology, cognitive science, robotics and neuroscience. In studying the hippocampal formation, it is fruitful to think of path integration as a computation that transforms a sense of motion into a sense of location, continuously integrated with landmark perception. Here, we review experimental evidence that path integration is intimately involved in fundamental properties of place cells and other spatial cells that are thought to support a cognitive abstraction of space in this brain system. We discuss hypotheses about the anatomical and computational origin of path integration in the well-characterized circuits of the rodent limbic system. We highlight how computational frameworks for map-building in robotics and cognitive science alike suggest an essential role for path integration in the creation of a new map in unfamiliar territory, and how this very role can help us make sense of differences in neurophysiological data from novel versus familiar and small versus large environments. Similar computational principles could be at work when the hippocampus builds certain non-spatial representations, such as time intervals or trajectories defined in a sensory stimulus space.

Summary: Path integration is one of the fundamental computations giving rise to the cognitive map and possibly other non-spatial representations in the hippocampal formation and its subcortical afferents.

Introduction

In essence, path integration is an internal computation that transforms a sense of motion into a sense of location. It requires tracking angular movements and distances traveled to estimate one's current position and orientation relative to a world-based (‘allocentric’) frame of reference. Mathematically, this estimate is a vector in a system of positional and directional coordinates associated with the allocentric reference frame. Position and orientation combined together are termed a ‘pose’ in mobile robotics and sometimes in biology (e.g. Heinze et al., 2018; Thrun et al., 2005) – not to be confused with a more comprehensive account of an animal's posture (e.g. Mimica et al., 2018). If path integration is calculated in a step-wise manner, the new pose update can be obtained by adding a movement vector estimating changes in position and orientation to the last pose update. If not, a continuous pose update can be obtained by integrating in time momentary angular and linear velocities. In either case, the necessary inputs are assumed to be derived from self-motion (‘idiothetic’) cues produced by locomotion (Barlow, 1964; Etienne et al., 1996; Etienne and Jeffery, 2004; Gallistel, 1990; McNaughton et al., 2006). These cues are typically internally generated, such as vestibular (inertial) cues, proprioceptive cues or motor efference copy (e.g. step counting). Hence, path integration is sometimes defined as the processing of these internal cues. However, some idiothetic cues that are not internally generated can be used for path integration, for example, optic flow, airstream detection (e.g. by a rat's whiskers) or other sensory reafference inputs produced by locomotion. Comparable sensors (gyroscopes, odometers, etc.) afford the application of path integration to artificial systems ranging from ships to robots.

To further complicate a comprehensive definition of path integration, the term is sometimes used to refer to components of the general problem of pose estimation. For example, a source of reliable directional information may be available, such as a compass to a sailor or polarized skylight to a desert ant (Fent and Wehner, 1985). In these instances, directional uncertainty is largely removed on a short time scale (on longer ones, compass recalibration or sun movements still need to be dealt with), and path integration only concerns the estimate of position. Vice versa, a process conceptually and computationally equivalent to path integration can be applied to a purely directional reference frame – based on the integration of angular velocity to update orientation irrespective of position – as occurs in the nervous system (Green et al., 2017; Knierim and Zhang, 2012; Skaggs et al., 1995; Taube, 2007; Turner-Evans et al., 2017; Zhang, 1996).

Path integration is typically conceptualized as supporting a navigation strategy that is complementary to ‘allothetic’ navigation. Allothetic navigation makes direct use of distinctive and stable environmental features and of the allocentric spatial relationships they specify. Where perceptual access to these landmarks is interrupted, path integration can be used for continued self-localization. But the pose estimate obtained by path integration in these conditions is expected to drift as a result of sensory and computational noise accruing over time, and therefore allothetic cues are required to prevent or correct this cumulative error.

Because allothetic and idiothetic navigation are often imagined as alternating behavioral strategies depending on the momentary availability of particular spatial inputs, path integration is often considered in isolation from landmark processing. This view originates in at least two contexts. In maritime navigation, self-localization in the open sea, where charted features are out of sight, represented an inescapable and critical problem for centuries until the advent of contemporary technology such as GPS. This problem was addressed via formal path integration calculations carried over a map by a ship officer. These calculations were referred to as ‘dead reckoning’ and must have contributed in no small measure to the formulation of the concept of path integration as was later used in biology (Gallistel, 1990). To demonstrate that animals are capable of path integration/dead reckoning via behavioral analysis, the experimenter must subject an animal to a (temporary) removal of allothetic cues or choose an animal that evolved to pay limited attention to these cues owing to exceptional ecological constraints (such as the desert ant; Wehner and Srinivasan, 1981). These experimental settings may reinforce the operational views of path integration as a standalone computation and of allothetic versus idiothetic navigation as functionally segregated strategies.

List of abbreviations.

BVC

 boundary vector cell

HD

 head direction

MEC

 medial entorhinal cortex

MS

 medial septum

SLAM

 simultaneous localization and mapping

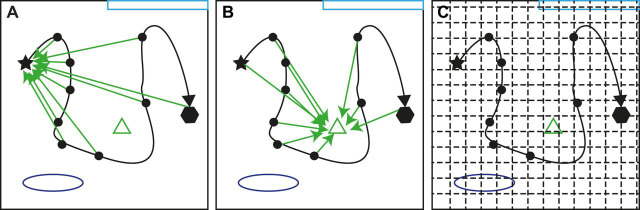
A separate issue is that the behavior called ‘homing’ and the computation called ‘path integration’ are often conflated in the animal behavior literature. Homing refers to an organism's navigation to a home base, often the starting point of a journey. It is the most common behavior used to study path integration, because it is ethologically natural, requires little training, is easy to measure and can be performed in the absence of allothetic landmarks. Because of this prevalence, path integration is often referred to as the process of updating a homing vector. However, homing and path integration are distinct concepts. The behavior of homing can be solved with navigation strategies other than path integration (e.g. a beacon that identifies the home base or starting point). Conversely, the computation of path integration can be used to continuously update a homing vector (Fig. 1A), but it can also be used to update a vector representation to any other fixed point in the environment (Fig. 1B) or to update a position coordinate on a map (Fig. 1C).

Fig. 1.

Possible neural representations of position based on path integration. (A) A homing vector. (B) A vector to a landmark in the environment. (C) A position in a Cartesian coordinate system. Each figure represents an organism's trajectory (black line) from a starting point (black star) to an end point (black hexagon) through an environment that contains landmarks (colored shapes).

Here, we adopt a view of path integration as a continuous pose update that works in tandem, as opposed to alternately, with landmark processing – relative to an arbitrary (but stable) metrical coordinate system (the scenario in Fig. 1C). This view is particularly relevant to the hippocampal cognitive mapping system of the mammalian brain (Etienne and Jeffery, 2004; McNaughton et al., 1996; O'Keefe, 1976; Redish and Touretzky, 1997), where the neural computations underlying path integration and landmark processing are likely to be highly integrated.

Path integration is implicated in fundamental properties of place cells and their interpretation as a cognitive map

Place cells and other spatial cells found in the hippocampal formation signal the position of the animal with respect to an allocentric frame of reference, like the ‘you-are-here’ tag found on a map. After O'Keefe and Dostrovsky's (1971) initial report on place cells, early experimental efforts were dedicated to demonstrating that place cell activity reflected self-localization relative to a cognitive abstraction of allocentric space – the ‘cognitive map’ – and not merely a collection of landmark views or local stimuli that vary systematically with the animal's position (Knierim and Hamilton, 2011). These studies confirmed that place cells can continue to track location when the allothetic spatial cues were removed (Gothard et al., 2001; Quirk et al., 1990; Save et al., 1998), thus implicating idiothetic cues and path integration in the expression of the place cells' firing fields. One of the earliest and most insightful investigations was that of O'Keefe and Speakman (1987), who showed that place fields on a plus maze were controlled by an array of distal landmarks when this array was rotated relative to the maze. However, the place fields could fire in the correct locations on the maze even when the landmarks were removed, as long as the rat was allowed a brief perceptual ‘registration’ period beforehand. Although the rat was confined to a small area of the apparatus during the registration period, place fields were later correctly recalled even when the rat occupied locations outside of this area. These observations revealed a persistent encoding of allocentric self-location and a mechanism capable of extrapolating the registration experience to the remainder of a previously learned map (see also Quirk et al., 1990). Save and colleagues (1998) subsequently showed that blind rats can produce normal place fields in an open arena in which the only salient orientation cues were a peripheral configuration of three objects. Remarkably, reproducible place fields were created even away from these objects. As with sighted rats in a similar apparatus (Cressant et al., 1997), the place fields followed rotation of the object configuration – including place fields located far away from the objects – after the animal had the opportunity to contact the objects. These observations revealed the ability of the place cell representation to persist when the familiar landmarks were not readily available, as well as to interpolate positions ranging between these landmarks.

Although other experiments have corroborated the role of idiothetic cues and the fundamental role played by path integration in hippocampal representations (e.g. Gothard et al., 1996; Terrazas et al., 2005; Bjerknes et al., 2018; Arleo et al., 2013; Knierim et al., 1995, 1998; Sharp et al., 1995; Knierim, 2002; see Moser et al., 2017 for a comprehensive review), direct investigations have proved more challenging than those addressing allothetic cues and landmark processing. Classic laboratory tasks do not lend themselves to the continuous manipulation of idiothetic cues as required by the analysis of path integration, and they are typically limited in space, making it difficult to reveal path integration errors presumably occurring at more ethologically relevant spatial scales. The advent of virtual reality systems has helped overcome some of these limitations (Harvey et al., 2009; Chen et al., 2013; Ravassard et al., 2013; Jayakumar et al., 2019). The discovery of grid cells (Hafting et al., 2005) has further provided new opportunities to make inroads into the neural basis of path integration in the cognitive map.

Grid cells probably reflect path integration and its interaction with allothetic information

Since their discovery in the medial entorhinal cortex (MEC) (Hafting et al., 2005) and the adjacent para- and pre-subiculum areas (Boccara et al., 2010), ‘grid cells’ have offered a fruitful clue into the neural substrate of the metrics of the cognitive map. A single grid cell fires at regular intervals in space, yielding a hexagonal grid of place fields (or, more precisely, a regular grid of equilateral triangles) that spans the full navigation range available to the animal (Figs 2B and 3A). Grid patterns of different cells vary in scale, orientation and phase (Barry et al., 2007; Stensola et al., 2012), and they can maintain consistent geometric relationships to each other across environments or experimental manipulations (Fyhn et al., 2007; Savelli et al., 2017; Yoon et al., 2013).

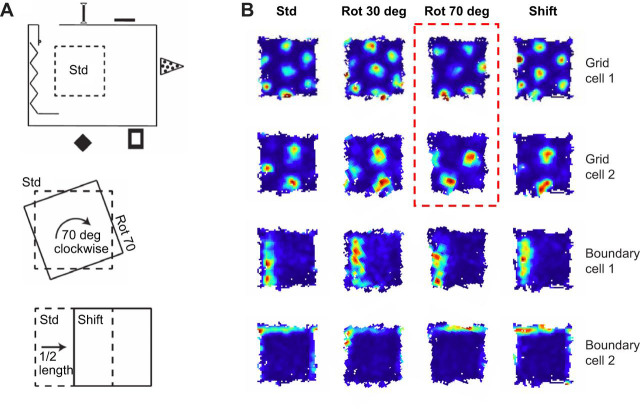
Fig. 2.

Grid and boundary cells in affine transformations (I). (A) Schematic of an experimental apparatus in which rats foraged on a 1.4×1.4 m platform [standard (Std)] placed in a room enriched with remote visual cues (top). This platform was rotated (Rot)/shifted (Shift) between recording sessions (center and bottom). (B) Example of two grid cells of different scale and two boundary cells that were recorded simultaneously across consecutive manipulations. The color code in each rate map represents the average firing rate of the cell in each position on the platform (red: high firing rate; blue: lack of activity). The rate maps have been rotated to a common orientation so as to aid visual comparison. The geometric relationships between each grid pattern and the boundaries (as well as the firing fields of the boundary cells) remain constant across most manipulations, consistent with the idea that boundary cells can predictably anchor the grid representation to an allocentric reference frame. However, in some cases, these relationships can be reconfigured because the grids drifted relative to the platform reference frame (marked by dashed red lines) while controlled by distal cues (not illustrated). Adapted from Savelli et al. (2017).

Fig. 3.

Grid and boundary cells in affine transformations (II). Rate maps of grid cells (A) and boundary cells (B) recorded first in a small box (58×58 cm) and then in a larger box (135×135 cm) in a single, uninterrupted session (these cells were not simultaneously recorded). Darker shades indicate a higher level of firing. Dashed red line indicates the prior position of the small box in the large box. The larger box revealed the qualitatively different firing patterns of these two types of cells, but in the small box it is usually impossible to tell one type from the other just based on the appearance of their firing fields (compare, for example, cell in A versus cell in B on each row). The specific influence of grid cells on downstream place cells is thus likely to become greater in larger environments where the rat can travel far from the boundaries encoded by boundary cells. Data from Savelli et al. (2008).

Every grid cell develops firing locations in any environment (Fyhn et al., 2007; Hafting et al., 2005). It is hard to imagine how the geometric arrangement of these firing locations could be directly imparted by a matching arrangement of environmental stimuli, in every environment and for all the different coexisting grids. Rather, an internal process seems at play, which geometrically interrelates environment locations that are experienced serially, based on a metric inherent in the animal's movements. Path integration is an obvious candidate for this process, as it can be used to keep track of the distance between grid firing positions relative to a single coordinate frame (Fig. 1C). Intermixed anatomically with grid cells are neural correlates of speed, direction and conjunctive location×direction (Cacucci et al., 2004; Sargolini et al., 2006; Kropff et al., 2015) that conjure the tell-tale computational signatures of a path integrator at work in the hippocampal formation (discussed below). Moreover, genetic manipulations of entorhinal cells support a causal role of these cells in the behavioral performance of tasks requiring path integration (Gil et al., 2018; Tennant et al., 2018; but see Bjerknes et al., 2018 for evidence that place cells can reflect path integration in darkness before well-formed grid cells develop postnatally). Accordingly, theoretical models implicate grid cells in path planning functions (Banino et al., 2018; Bush et al., 2015; Erdem and Hasselmo, 2012, 2014; Kubie and Fenton, 2012; Stemmler et al., 2015), and several computational models of grid signal generation are based on neural models of path integration (discussed below). Grid-like firing has also been shown to emerge in general-purpose machine-learning systems trained to perform path integration (Banino et al., 2018; Cueva and Wei, 2018 preprint). [Models of grid cells that are not formally based on path integration have nonetheless been proposed (Franzius et al., 2007; Kropff and Treves, 2008; Si and Treves, 2013; Urdapilleta et al., 2017; Weber and Sprekeler, 2018).]

However, in spite of path integration being an inherently noisy computation, the firing patterns of grid cells remain spatially stable over prolonged and repeated trials, suggesting that landmarks provide a spatial reference for path integration. In other words, while the grid spatial code seems to reflect the animal's ability to egocentrically parse the metrical structure of the external world by path integration, the resulting neural representation is nonetheless allocentric. Prominent landmarks that exert strong influence over spatial behavior are the geometric boundaries of the environment (Cheng, 2008, 1986; Cheng and Newcombe, 2005; Tommasi et al., 2012). Based on the responses of place cells to boundary manipulations, Burgess, O'Keefe and colleagues proposed the existence of ‘boundary vector cells’ (BVCs) (Barry et al., 2006; Hartley et al., 2000; O'Keefe and Burgess, 1996). A BVC is postulated to fire whenever the animal is at a certain distance from any boundary in a certain allocentric direction. Subsequent experimental studies discovered cells that encoded the animal's position relative to boundaries – the walls or edges constituting the perimeter of the recording arena (‘boundary’ or ‘border’ cells) (Lever et al., 2009; Savelli et al., 2008; Solstad et al., 2008) (Figs 2B and 3B). Boundary cells are intermixed with grid cells in all brain areas where the latter have been also found (with perhaps the exception of the subiculum, which does not seem to contain grid cells, but see Brotons-Mas et al., 2017; Sharp, 1999). Do boundary cells functionally complement path integration by endowing the grid representation with allocentric properties? Recent analyses have shown that the positional signal encoded by grid cells tends to drift in open space until the animal encounters a boundary, where the drift is corrected by ‘resetting’ the encoded position (Hardcastle et al., 2015). Because a drift is indeed expected to occur because of accumulating errors in path integration, this finding is consistent with the idea that synaptic inputs from boundary cells episodically reset a grid cell signal that is produced continuously through path integration (Barry et al., 2007; Burgess et al., 2007; Cheung et al., 2012; Fuhs and Touretzky, 2006; Hasselmo, 2008; Knierim and Hamilton, 2011; McNaughton et al., 1996; Redish and Touretzky, 1997; Savelli et al., 2008; Solstad et al., 2008; Zhang et al., 2014). The consistency of these corrections across boundaries guarantees that this signal is transformed into a proper allocentric representation.

There are, however, two caveats concerning the relationship between grid cells, boundary cells and path integration. First, grid firing patterns can exhibit elliptical compression/stretching, shearing or other types of distortion (Barry et al., 2007; Krupic et al., 2015; Savelli et al., 2017, 2008; Stensola et al., 2012, 2015). Some of these distortions can develop in time-averaged data plots if different boundaries reset the grid in a slightly inconsistent way relative to a single reference frame (Keinath et al., 2018). If so, the distortions observed in these plots result, to some degree, from the allocentric ‘jittering’ of the coordinate system produced by encountering specific boundaries, rather than from metrical errors of the path integrator. An alternative interpretation of the grid distortions is that the grid representation is not a universal metric for the cognitive map; rather, it purposely reflects the geometric peculiarities of the environment (Krupic et al., 2016). Resolving the function and origin of grid distortions is a crucial future direction in grid cell research as it promises to reveal more of their function and neural mechanisms, especially as to their relation with path integration and with path integration's computational limits in the rat.

A second caveat concerns the likely existence of other strategies for stabilizing the grid representation besides the use of boundaries. The grid representation can be distally controlled by remote landmarks beyond the navigation range experienced by the animal, causing grids to geometrically dissociate from both the physical local boundaries and their neural representation via boundary cells (Savelli et al., 2017) (Fig. 2B). This scenario implies a plastic relationship between grid and boundary cells, which may be reconfigured by BVCs anchoring the grid representation to the remote laboratory walls, or by landmark vector cells (Deshmukh and Knierim, 2013, 2011; Hoydal et al., 2018 preprint; McNaughton et al., 1995; Wilber et al., 2014) doing the same relative to discrete remote landmarks (or by a yet-undiscovered representation of the geometrical center of the environment; see discussion in Savelli et al., 2017).

The ubiquitous, ‘universal’ manifestation of grid cells' periodic firing patterns in any environment evokes the image of a reusable stock of graph paper on which cognitive maps could be charted at multiple spatial resolutions. Does the grid cell system set the metrics and reference frame for the whole cognitive map across the hippocampal formation (Moser and Moser, 2008)? A recent study shows that place-cell maps inherit at least some of the grid-map geometrical properties, as knockout of HCN1 channels in the MEC increased the scale of the grids in the MEC as well as place field size in the downstream hippocampus (Mallory et al., 2018). The influence of grid inputs on the place-cell map is additionally supported by experimental manipulations of entorhinal cells leading to place cell ‘remapping’ (Fyhn et al., 2007; Kanter et al., 2017; Miao et al., 2015; Rueckemann et al., 2016).

Where, and how, does path integration occur?

There seem to be at least two main scenarios to consider for the anatomical and computational origin of path integration contributions to hippocampal cognitive maps.

Cortical attractors

In the first scenario, path integration is computed in the cerebral cortex, in the MEC and possibly in other cortical regions of the hippocampal formation. Putative path integration inputs are present in the MEC in the form of velocity signals. Speed is encoded in multiple ways (Hinman et al., 2016) by speed cells (Kropff et al., 2015), by speed-modulated firing rates of spatial cells (Sargolini et al., 2006) or by the exact frequency of theta-modulated bursts of these cells (Jeewajee et al., 2008). Orientation can be provided by head direction (HD) cells (Sargolini et al., 2006), which fire selectively when the animal's head is pointed in a particular allocentric direction (Taube, 2007) (but see Raudies et al., 2015 for a discussion about a critical difference between head and moving direction). Putative path integration outputs – or its intermediate computational results – are also present in the MEC in the form of allocentric positional and directional representations encoded by grid cells (Hafting et al., 2005), grid×HD cells (Sargolini et al., 2006) and possibly other non-periodic spatial cells (Diehl et al., 2017; Hardcastle et al., 2017; Keene et al., 2016). This collection of experimental phenomena supports models of grid-pattern generation by path-integration-performing ‘continuous attractor’ networks (Knierim and Zhang, 2012; McNaughton et al., 2006). In this class of models, a persistent pattern of neural activity (the ‘activity bump’) propagates through the network in lockstep with the animal's locomotion, guided by velocity signals and mediated by recurrent connections. If the network is topologically arranged as a torus, any cell fires every time the bump returns to the same cell, possibly after completing an arbitrary loop around the torus, thus giving rise to a rectangular grid of firing fields repeating in space (McNaughton et al., 2006). If the neural connections on the torus are systematically twisted, this grid becomes rhomboidal (instead of rectangular), similar to that expressed by a real grid cell (Guanella et al., 2007). Alternatively, multiple bumps are continuously generated and move in concert in the network. Repeating fields in this case result from different bumps riding over the same cell. The hexagonal pattern of bumps that would make the cell fire as a real grid cell can spontaneously emerge in such a network if lateral excitation and inhibition are fashioned as a Turing reaction–diffusion system (Burak and Fiete, 2009; Fuhs and Touretzky, 2006; McNaughton et al., 2006). More recently, the recurrent connections between putative grid cells were primarily found to involve inhibitory interneurons, and attractor models have been successfully refined to accommodate this finding (Couey et al., 2013; Pastoll et al., 2013; Shipston-Sharman et al., 2016).

Subcortical oscillators

In the second scenario, only allothetic information is processed cortically, whereas path integration computations are carried out subcortically, similar to the anatomical and computational organization of the HD cell system (Blair et al., 2008). Like place and grid cells, HD cells also depend on the consistent processing of both idiothetic and allothetic cues, albeit restricted to a purely angular reference frame. The HD signal originates from subcortical regions processing angular velocity signals, presumably based on motor and vestibular inputs (Cullen and Taube, 2017; Taube, 2007). This signal then reaches the cortical postsubiculum, where it is aligned with visual landmarks (Goodridge and Taube, 1997). Last, the landmark-aligned signal is fed back to the same subcortical areas where the HD signal originated (Yoder et al., 2015). Thus, the HD representation is initiated in subcortical circuits performing angular path integration, but its allocentric character is acquired in a cortical area and propagated back to the originating circuits, to ensure the coherence of the internal sense of direction throughout the brain.

The cortical versus subcortical contributions to the place/grid cell system may be similarly organized. First, the positional signals of this system could be initiated via path integration in the medial septum (MS) or upstream of it. The MS contains theta cells, which are interneurons modulated by the 6–12 Hz theta rhythm that dominates hippocampal activity during locomotion (see Buzsáki, 2002 for a review). The bursting frequency of these cells is modulated by speed and direction of locomotion (King et al., 1998; Welday et al., 2011), providing a representation of velocity based on a temporal code. They have been proposed to additionally encode the position of the animal via their relative theta firing phase – a ‘phase code’ (Blair et al., 2008; Monaco et al., 2011; Welday et al., 2011) – building on previous theoretical work on ‘velocity-modulated oscillatory interference models’ (Burgess et al., 2007; Hasselmo et al., 2007). The proposed neural architecture comprises subcortical banks of velocity-modulated ‘ring attractors’ (Blair et al., 2014, 2008; Burgess and Burgess, 2014), in which a bump of activity is hypothesized to periodically traverse a network that is topologically arranged as a ring. Each ring works as a path integrator that tracks the distance traveled in a particular direction by the velocity-modulated precession of its phase relative to a reference theta oscillation. Ring attractors had previously been hypothesized to explain angular path integration in HD cells (Cullen and Taube, 2017; Green et al., 2017; Kim et al., 2017; Knierim and Zhang, 2012; Turner-Evans et al., 2017). Thus, path integration in two-dimensional space may have evolved by duplicating and repurposing pre-existing subcortical circuitry originally dedicated to a one-dimensional version of ‘path integration’ in angular space for HD cells (Blair et al., 2008). Besides the work of Welday et al. (2011), recent studies have implicated the MS in the processing or relaying of idiothetic information (Fuhrmann et al., 2015; Hinman et al., 2016; Justus et al., 2017).

Second, the positional estimate represented by the distribution of phases across the subcortical bank of velocity-controlled ring attractors may be projected to cortical areas such as the MEC (Gonzalez-Sulser et al., 2014; Justus et al., 2017). Here, this signal would be allocentrically reconciled with the representations of boundaries or other landmarks. Grid cells could be a neural product of this process, whereby the subcortical phase-coded output is converted to a rate code that is presumably more amenable to the type of cortical plasticity necessary to bind it to landmark representations (Blair et al., 2014, 2008; Burgess and Burgess, 2014; Burgess et al., 2007; Evans et al., 2016; Hasselmo et al., 2007; Hasselmo and Brandon, 2012). MS pharmacological inactivation severely disrupts the firing patterns of grid cells, although they can still display multiple place fields (Koenig et al., 2011) and preserve any directional modulation (Brandon et al., 2011), suggesting that the disruption is specific to the processing or relaying of metrical information to the grid cell system. Accordingly, rats' ability to estimate linear distances is impaired after MS lesions (Jacob et al., 2017), and the firing locations of place cells shift toward landmarks during MS inactivation (Fattahi et al., 2018).

Last, the allocentric stabilization produced in these cortical areas – or as further processed by the hippocampus proper – would be relayed back to the subcortical representations, making them allocentric as well. Indeed, neurons of the lateral septum signal allocentric self-position by both firing rate and theta phase (Leutgeb and Mizumori, 2002; Takamura et al., 2006; Tingley and Buzsáki, 2018; Monaco et al., 2019), while neurons in other subcortical areas also encode position by firing rate (Jankowski et al., 2015; Jankowski and O'Mara, 2015). [Similarly, speed is encoded both by rate and phase in the MEC, but with a  different degree of sensitivity to MS lesions (Hinman et al., 2016).]

What is path integration good for in the mammalian brain?

In all the scenarios considered above, path integration is viewed as a continuously operating, automatic process closely integrated with landmark processing. Although this computational strategy has long been central to certain theoretical views of hippocampal function (Etienne and Jeffery, 2004; McNaughton et al., 1996; O'Keefe, 1976; Redish and Touretzky, 1997; Taube, 2007), it found practical validation and mathematical formulations in the field of mobile robotics (Thrun et al., 2005). Here, the robot's perceptual and spatial uncertainty is explicitly quantified by probability distributions over a suitable set of random variables modeling: (1) noisy sensory inputs (from both idiothetic sensors, such as odometers and gyroscopes, and allothetic ones, such as cameras, sonar and laser range finders); (2) the effect of locomotor commands (also an idiothetic cue by analogy to motor efference copy); and (3) the robot's pose (i.e. its position and orientation relative to the allocentric reference frame) – all with respect to a given map. Bayesian algorithms perform continuous autonomous localization as a live update of the probability distribution on (3) by integrating the information from (1) and (2) (Fig. 4).

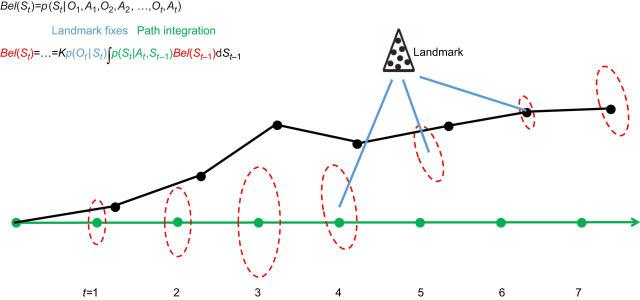
Fig. 4.

Path integration and landmark processing are closely integrated in recursive Bayesian filters for robot self-localization. A ‘belief’ on a state is modeled as a random vector and its multidimensional probability distribution. The cartoon illustrates a self-localization problem where S_t is a pose, and the associated posterior distribution Bel(S_t) is conditioned to the history of locomotion actions A₁…A_t and landmark observations O₁…O_t, i.e. all that the robot knows. The robot sets on a linear path by sending a series of identical forward motor commands to its wheel actuators (green). The actual path followed by the robot (black) drifts from the intended path. At each step, an update of the self-location estimate is given by recursive equations that calculate Bel(S_t) from Bel(S_t–1). The term p(O_t|S_t) is a conditional distribution on the landmark observations given the current state – it contributes landmark fixes to self-localization. The term p(S_t|A_t,S_t–1) is the conditional distribution on the possible current poses given the action just taken and the previous pose – it contributes path integration to self-localization. The dashed ellipses denote the mean and variance of Bel(S_t) derived by the filter at each step (heading is not represented in this illustration), i.e. they represent the robot's belief of where it is and its associated degree of confidence. When the landmark is out of sight, p(O_t|S_t) is not informative, and both spatial error and uncertainty grow. When the landmark becomes visible (steps 4–6), both p(O_t|S_t) and p(S_t|A_t,S_t–1) meaningfully contribute to the estimate, and the landmark is used to reduce both the error and uncertainty (see Thrun et al., 2005 for more details). Note how path integration and landmark fixes are seamlessly and dynamically integrated in this mathematical framework. The idiothetic cue used for path integration in this example is akin to a biological motor efference copy. Other idiothetic cues can also be used, such as given by a gyroscope (vestibular system), odometer (proprioceptive inputs), etc. Also note that p(O_t|S_t) contains information on what landmark observations are expected at any pose, i.e. it amounts to a map of the environment given to the robot.

Because of its clear computational abstraction, the Bayesian framework may help refine and advance theoretical thinking on hippocampal spatial function (Cheung, 2016; Erdem et al., 2015; Finkelstein et al., 2016; Kanitscheider and Fiete, 2017; Touretzky et al., 2005). Concerning the role of path integration, one advantage of its continuous integration in the process of self-localization may be a rapid, moment-by-moment updating of the position estimate. Landmark identification and distance estimation relative to an internal map are presumably slower perceptual and cognitive processes than the mathematical integration of acceleration/velocity signals, which can be produced in thalamic or primary sensory areas, and partly during sensory transduction (e.g. with vestibular inputs). A system that activated path integration computations only when landmarks become unavailable would arguably be less reactive to rapid movements compared with a system that continually employed path integration; that is, a ‘quick and dirty’ update from path integration (later corrected by landmarks if needed) may be better than a delayed update directly from landmarks. A further related advantage of path integration for navigation is a more reactive response to the sudden or intermittent occlusion of key landmark inputs, for example, in darkness. The equation in Fig. 4 would simply account for this situation as a temporary lack of allothetic inputs in the corresponding term of the equation. These inputs would therefore be subtracted from the self-localization computations, leaving path integration alone performing this job, rather than path integration being added as a ‘backup’ system – a mechanistic difference that may be difficult to detect in behavioral studies.

The tremendous success of the Bayesian approach to mobile robotics, however, is best proven in situations where the robot is not given a reliable map but needs to build it from scratch in the process of exploring a novel environment. In this situation – called concurrent mapping and localization (CML) or simultaneous localization and mapping (SLAM) (Thrun et al., 2005) – the robot faces a chicken-or-egg problem: it needs a map with respect to which it can perform self-localization, but it needs accurate self-localization to stitch together its perceptual views into a map. Therefore, the map itself is subject to uncertainty and it too must be represented by a complex set of multidimensional random variables and their associated probability distributions. SLAM can be solved by a recursive Bayesian update of the joint distribution on the pose and map, thus embracing the circular nature of this problem, but at the cost of adding considerable computational complexity to its algorithmic solution (Thrun et al., 2005) (Fig. 5).

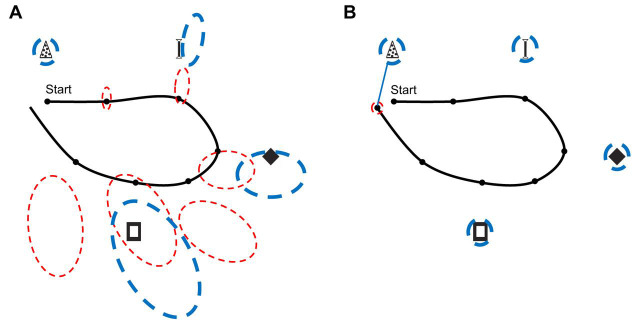
Fig. 5.

Path integration and landmark processing in robot simultaneous localization and mapping (SLAM). In this case, a distribution on the observations of landmarks such as p(O_t|S_t), described in Fig. 4, is not given to the robot. Instead, a map needs to be built during the exploration of the environment. A circular problem arises in which a map is needed for self-localization, but accurate self-localization relative to this map is needed to extend it to new territory. In this example, the map is a collection of unknown allocentric coordinates for consecutively encountered landmarks. This information can be modeled as a random vector M, so that the goal of the robot is to estimate its joint belief on both the map and its pose relative to it: p(S_t ,M|O₁,A₁,O₂,A₂,…,O_t ,A_t) (compare with target belief distribution in Fig. 4, in which M does not appear). This problem can still be addressed by recurrent Bayes filters similar in principle to those described in Fig. 4, but with greater mathematical complexity and computational cost. (A) The robot's path is depicted in black, the distribution on its pose at each step is depicted by the fine-dashed ellipses (red) as in Fig. 4, and the distributions on the allocentric landmark poses (contained in M) are similarly depicted as coarse-dashed ellipses (blue). Note how the spatial error and uncertainty progressively grow along the trajectory as in Fig. 4 for both the robot and the landmark poses – unlike in Fig. 4, the landmarks are not useful for self-localization the first time they are encountered. (B) However, when the robot comes back to a position where the first landmark is recognized, the Bayesian algorithm is able to reduce at once the error and uncertainty on its current pose (small red ellipse) and all the landmark poses (shrunken blue ellipses), because the relationships between robot and landmark poses had been embedded along the way within a single coordinate system. These relationships, however erroneous at first, are initially afforded by path integration. Further excursions beyond the initial trajectory can iteratively build up a representation of an extended environment. Other types of map representations, and various mathematical formulations and algorithmic strategies for Bayesian solutions to SLAM, are reviewed in Thrun et al. (2005).

The intuitions derived by this engineering framework converge with theoretical insights from ethological, behavioral and cognitive studies (Fig. 6A) (Gallistel, 1990), in which some form of path integration is deemed necessary for integrating egocentric percepts into a consistent allocentric representation (Alexander and Nitz, 2017, 2015; Byrne et al., 2007; Holmes et al., 2018; Nitz, 2009, 2006; Peyrache et al., 2017; Whitlock et al., 2012; Wilber et al., 2014; Wang et al., 2018). When the map of a new environment is first learned, landmarks are of no immediate help for correcting path integration drift if they are not first charted relative to the allocentric reference frame in use, a task requiring path integration to begin with (Fig. 5). Consideration of how animals explore novel environments is informative here (see also review by Thompson et al., 2018). In a new environment, animals quickly adopt a ‘home base’, often near a salient landmark (Hines and Whishaw, 2005; Wallace et al., 2002), from which they initiate bouts of exploratory excursions and to which they frequently return (Eilam and Golani, 1989). Initial excursions are short, characterized by forward movement interspersed with intermittent pauses (Benjamini et al., 2011; Golani et al., 1993; Kramer and McLaughlin, 2001). During these pauses, animals engage in a behavior called ‘head scanning’, in which they perform lateral head movements to gather information about landmarks and other sensory information available at that location. This behavior has been associated with the rapid, one-shot formation of new place fields at the site of the scan (Monaco et al., 2014; see also Bittner et al., 2017; Diamantaki et al., 2018; Dragoi et al., 2003; Frank et al., 2004). Successive excursions originating from and returning to the home base (interleaving forward motion with head scanning epochs) cover ever-increasing areas of the environment. It is likely that that this pattern of behavior reflects nature's solution to the SLAM problem. During the initial, brief excursion, the animal updates its position based on path integration, providing a spatial framework upon which landmarks are incorporated during head scans. Before excessive path integration error can accumulate, the animal returns to its home base, where any small error can be corrected and the path integrator coordinate system can be reset. Because of the incorporation of landmarks in the initial excursion, the animal can explore a larger area of terrain on its next excursion, as the landmarks prevent error accumulation during the portion of the excursion that repeats the first excursion. Thus, with this iterative process, in which path integration sets the metric of a spatial framework upon which allothetic cues are bound, the animal is able to construct a map of a novel environment. [It is important to keep in mind that compartmentalized environments and large-scale spaces may not be mapped within a single reference frame. Alternative mapping strategies have been the subject of multidisciplinary research (e.g. Derdikman et al., 2009; Kuipers, 2000; Kuipers et al., 2004; Nitz, 2009; Redish, 1999).]

Fig. 6.

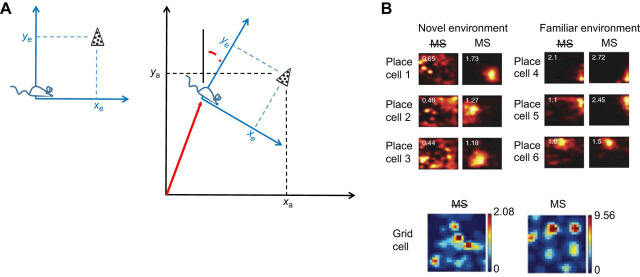
Converging insights into the role of path integration in map building: cognitive models and neurophysiological data are broadly consistent with approaches to robot SLAM. (A) Behavioral studies suggest the existence of map-like cognitive representations in many species. In a novel environment, such a representation needs to be populated by salient environmental features. These features are egocentrically perceived (e.g. coordinates x_e,y_e of a visual landmark, left plot), but they eventually need to be charted relative to the stable allocentric reference frame adopted for the map (coordinates x_a,y_a, right plot). This can be achieved mathematically by a coordinate transformation (translation+rotation) based on parameters derived from path integration (red translation vector and rotation angle in red defining the animal's pose in the map frame, right plot). Albeit much simpler, this general model assigns a similar role to path integration in map-building as does the SLAM framework of Fig. 5. [See fig. 5.1 of Gallistel (1990) for more details and analysis extended to algebraic representations of curves and surfaces, reminiscent of the boundaries of an environment.] (B) One implication of this perspective is that the disruption of path integration or its outputs should lead to reduced spatial modulation of the firing fields of place cells in novel environments, but not necessarily in familiar ones, where self-localization can rely on previously charted landmarks (as in Fig. 4). Top: place fields from the same place cells are disrupted in a novel, large enclosure if the medial septum is inactivated (MS with strikethrough), but not when the platform is highly familiar (adapted from Wang et al., 2015). Bottom: when the medial septum is inactivated, grid cells lose their characteristically regular firing pattern, which may be sustained by path integration (adapted from Koenig et al., 2011).

Recent observations appear consistent with the role of path integration in the creation of a new place cell map. As mentioned before, inactivation of the MS suppresses the regular structure in grid cell firing (Brandon et al., 2011; Koenig et al., 2011), consistent with the loss of path integration. In one experiment in a large, novel environment, place cells did not form spatial firing fields during MS inactivation (Wang et al., 2015) (Fig. 6B). If MS inputs (and/or grid cells) convey self-motion cues or the output of path integration per se (as discussed above), these observations are consistent with a pivotal role of path integration in creating allocentric representations of novel environments based on perceptual inputs that are egocentrically experienced, as pointed out by Gallistel (1990) and studied in SLAM (Figs 5 and 6A).

By contrast, in a similar experiment in a novel but smaller environment, CA1 place fields developed normally (Brandon et al., 2014). A possible explanation for this difference is that in a small enclosure, boundary cells can look indistinguishable from grid cells (Savelli et al., 2008) (Fig. 3); thus, place field formation may be less vulnerable to the disruption of grid inputs if boundary cells are spared. Moreover, path integration is probably less critical for self-localization or map-building in small environments. In familiar environments both small (Koenig et al., 2011) and large (Wang et al., 2015), CA1 place cells also seem to function normally during MS inactivation [although the spatial firing of CA3 place cells can be disrupted compared with control animals (Mizumori et al., 1989)]. In a familiar environment, place cells may be able to keep their firing fields by relying on previously learned associations with landmarks (i.e. the known map), even if path integration is compromised by MS inactivation (similar to the Bayes filter with a given map described in Fig. 4, but in which the path integration term is suppressed). Thus, future work could experimentally investigate whether these place cells regress to plain sensory representations of allothetic cues/relationships while losing the very properties that have historically implicated place cells in a genuinely abstract representation of space and that may be obtained through path integration. As discussed at the beginning of this Review, the crucial distinction is between a spatial firing correlate owing to a sensory cue (the cell fires at a corner) versus a place representation that is not dependent on any particular sensory feature. For example, it is known that in normal animals, place cells remain intact in darkness and/or in the absence of salient landmarks (Markus et al., 1994; O'Keefe and Speakman, 1987; Quirk et al., 1990); they can decouple completely from the set of local and global landmarks yet maintain their own internal coherence (i.e. the map can rotate coherently relative to all allocentric cues) (Knierim et al., 1998, 1995); and the cells can maintain firing when any subset of landmarks are available, showing that they do not rely on the presence of a specific sensory cue (O'Keefe and Conway, 1978). It will be important to determine whether place fields unaffected by MS inactivation have similar properties. Earlier studies showed that CA3 and CA1 place fields were present after MS lesions (Miller and Best, 1980; Shapiro et al., 1989), but the cells were less stable in darkness than in control animals (Leutgeb and Mizumori, 1999), and were more controlled by local cues on an apparatus than by global landmarks on the wall (Miller and Best, 1980). Control by peripheral landmarks such as global cues or environmental boundaries is associated with directional orientation and the MEC system (Knierim and Hamilton, 2011; Neunuebel et al., 2013; Savelli et al., 2017; Zugaro et al., 2001), whereas control by local cues has been associated with the lateral entorhinal cortex system (Neunuebel et al., 2013). Lesions of the MEC that leave the lateral entorhinal cortex intact compromise CA1 place fields in relatively larger and novel environments (see fig. 2C of Hales et al., 2014), similar to the MS inactivation experiment discussed above (Wang et al., 2015). Thus, there is some evidence in the literature to suggest that the spatial firing that survives MS inactivation and grid cell disruption in smaller or familiar environments may be the result of spatial computations based on local landmarks (Deshmukh and Knierim, 2011; Wang et al., 2018) rather than path integration.

Are path-integration-like computations used in non-spatial domains?

The neural circuitry and dynamics that allow path integration computations in the hippocampal system may also explain a number of other phenomenological properties of neurons in this system. A growing body of evidence shows that hippocampal cells that represent locations when the animal is moving (i.e. place cells) can also represent time when the animal is running in place or is otherwise stationary but attentive (Gill et al., 2011; Kraus et al., 2015, 2013; MacDonald et al., 2011; Pastalkova et al., 2008; Salz et al., 2016). Under other conditions, the cells encode the distance traveled along a path (Gothard et al., 1996; Kraus et al., 2015, 2013; Ravassard et al., 2013). These three phenomenologically distinct representations (space, distance and time), encoded by the same population of cells, can in principle be explained by a single computational mechanism, as shown by Hasselmo (2007) using the oscillatory interference model of Burgess and colleagues (2007). Two fixed oscillators produce an interference pattern with a temporally constant beat frequency of its envelope (i.e. a time cell). However, if one of the oscillators was variable and its frequency was appropriately modulated by the running speed of the animal, the beat frequency of the interference pattern envelope would be a function of the distance traveled along a path (i.e. a distance cell). Further, if the variable oscillator was appropriately modulated by both speed and movement direction (a movement/velocity vector), the beat frequency of the envelope would be a function of location (i.e. a place cell or grid cell). Thus, three distinct phenomenological properties of the same set of neurons can be explained and unified based on computational principles, as the output of the network was determined only by changes to the inputs that adjust the frequency of the variable oscillator. Although Hasselmo (2007) used oscillatory interference models to demonstrate the principle, in theory the principle can be applied to attractor network models of place cells and grid cells as well. In support of this principle, the time cell properties of hippocampal neurons in a running wheel were disrupted when the MS inputs were silenced, in the same way as place cells were disrupted in large and novel environments (Wang et al., 2015).

The same arguments can unify the path integration models with the apparent representation by hippocampal cells of non-spatial variables. In one experiment, stationary rats were trained to listen to an auditory tone of monotonically increasing frequency and release a lever within a small frequency window (Aronov et al., 2017). The firing of different hippocampal cells was correlated with different auditory frequencies. Although one might interpret this result as a completely different computation than path integration, it is actually completely consistent with the ideas expressed above. When the rat is stationary, one can assume that the network is in the mode in which it acts like a clock (i.e. time cells). How does one explain the auditory frequency tuning? Just as when the system performs path integration during movement, with the external landmarks able to correct error in the path integration output and keep it calibrated with the external world, the only salient external cue in the auditory experiment is the varying frequency of the tone. The same neural plasticity that ties landmarks or scenes to spatial representations during path integration would allow the auditory cues to control the exact timing of the hippocampal cells after experience.

Does this reasoning imply that the auditory responses are somehow an artifact? Not at all. Our point here is that understanding path integration as a computational mechanism allows a unifying explanation of seemingly disparate neurophysiological phenomena. The hippocampal circuitry likely evolved to perform ethologically critical spatial mapping functions, and later became co-opted by the opportunistic process of natural selection to allow the animals to solve other tasks using the same neural hardware and computational principles. More precisely, a system that evolved to rapidly bind landmarks onto a path-integration-based mapping system could subsequently evolve to perform other rapid binding tasks of diverse external sensory input onto a sequential code. This way of thinking may be the link between disparate viewpoints of the roles of hippocampus in spatial mapping in rodents and declarative memory in humans (Burgess et al., 2002; Buzsáki, 2005; Buzsáki and Moser, 2013; Eichenbaum et al., 2016, 1999; Lisman, 1999; O'Keefe and Nadel, 1978).