Fig. 4.

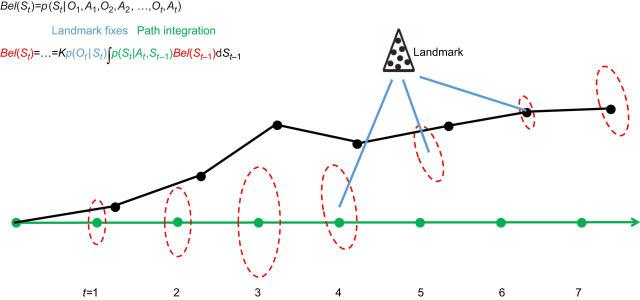
Path integration and landmark processing are closely integrated in recursive Bayesian filters for robot self-localization. A ‘belief’ on a state is modeled as a random vector and its multidimensional probability distribution. The cartoon illustrates a self-localization problem where S_t is a pose, and the associated posterior distribution Bel(S_t) is conditioned to the history of locomotion actions A₁…A_t and landmark observations O₁…O_t, i.e. all that the robot knows. The robot sets on a linear path by sending a series of identical forward motor commands to its wheel actuators (green). The actual path followed by the robot (black) drifts from the intended path. At each step, an update of the self-location estimate is given by recursive equations that calculate Bel(S_t) from Bel(S_t–1). The term p(O_t|S_t) is a conditional distribution on the landmark observations given the current state – it contributes landmark fixes to self-localization. The term p(S_t|A_t,S_t–1) is the conditional distribution on the possible current poses given the action just taken and the previous pose – it contributes path integration to self-localization. The dashed ellipses denote the mean and variance of Bel(S_t) derived by the filter at each step (heading is not represented in this illustration), i.e. they represent the robot's belief of where it is and its associated degree of confidence. When the landmark is out of sight, p(O_t|S_t) is not informative, and both spatial error and uncertainty grow. When the landmark becomes visible (steps 4–6), both p(O_t|S_t) and p(S_t|A_t,S_t–1) meaningfully contribute to the estimate, and the landmark is used to reduce both the error and uncertainty (see Thrun et al., 2005 for more details). Note how path integration and landmark fixes are seamlessly and dynamically integrated in this mathematical framework. The idiothetic cue used for path integration in this example is akin to a biological motor efference copy. Other idiothetic cues can also be used, such as given by a gyroscope (vestibular system), odometer (proprioceptive inputs), etc. Also note that p(O_t|S_t) contains information on what landmark observations are expected at any pose, i.e. it amounts to a map of the environment given to the robot.