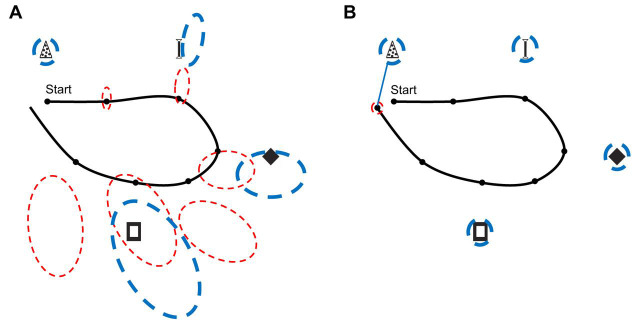
Fig. 5.

Path integration and landmark processing in robot simultaneous localization and mapping (SLAM). In this case, a distribution on the observations of landmarks such as p(O_t|S_t), described in Fig. 4, is not given to the robot. Instead, a map needs to be built during the exploration of the environment. A circular problem arises in which a map is needed for self-localization, but accurate self-localization relative to this map is needed to extend it to new territory. In this example, the map is a collection of unknown allocentric coordinates for consecutively encountered landmarks. This information can be modeled as a random vector M, so that the goal of the robot is to estimate its joint belief on both the map and its pose relative to it: p(S_t ,M|O₁,A₁,O₂,A₂,…,O_t ,A_t) (compare with target belief distribution in Fig. 4, in which M does not appear). This problem can still be addressed by recurrent Bayes filters similar in principle to those described in Fig. 4, but with greater mathematical complexity and computational cost. (A) The robot's path is depicted in black, the distribution on its pose at each step is depicted by the fine-dashed ellipses (red) as in Fig. 4, and the distributions on the allocentric landmark poses (contained in M) are similarly depicted as coarse-dashed ellipses (blue). Note how the spatial error and uncertainty progressively grow along the trajectory as in Fig. 4 for both the robot and the landmark poses – unlike in Fig. 4, the landmarks are not useful for self-localization the first time they are encountered. (B) However, when the robot comes back to a position where the first landmark is recognized, the Bayesian algorithm is able to reduce at once the error and uncertainty on its current pose (small red ellipse) and all the landmark poses (shrunken blue ellipses), because the relationships between robot and landmark poses had been embedded along the way within a single coordinate system. These relationships, however erroneous at first, are initially afforded by path integration. Further excursions beyond the initial trajectory can iteratively build up a representation of an extended environment. Other types of map representations, and various mathematical formulations and algorithmic strategies for Bayesian solutions to SLAM, are reviewed in Thrun et al. (2005).