Understanding and Controlling Food Protein Structure and Function in Foods: Perspectives from Experiments and Computer Simulations

Abstract

The structure and interactions of proteins play a critical role in determining the quality attributes of many foods, beverages, and pharmaceutical products. Incorporating a multiscale understanding of the structure–function relationships of proteins can provide greater insight into, and control of, the relevant processes at play. Combining data from experimental measurements, human sensory panels, and computer simulations through machine learning allows the construction of statistical models relating nanoscale properties of proteins to the physicochemical properties, physiological outcomes, and tastes of foods. This review highlights several examples of advanced computer simulations at molecular, mesoscale, and multiscale levels that shed light on the mechanisms at play in foods, thereby facilitating their control. It includes a practical simulation toolbox for those new to in silico modeling.

INTRODUCTION

The food industry is faced with multiple challenges to meet demands for new food products that are safe, enjoyable, healthy, nutritious, and sustainable. An understanding of fundamental structure–function relationships of food components is key to the rational design of new foods. A relatively recent approach to deal with the complexity of food products is provided by soft matter physics (Boire et al. 2019) (Figure 1). Molecules assemble through biological, physicochemical, or manufacturing processes into structures that give foods their particular properties. Oral processing and sensory stimulation followed by digestion lead to the disassembly of macroscopic structures down to the molecular level, ultimately making them bioavailable to cells. All these processes can be studied using soft matter physics techniques.

Figure 1.

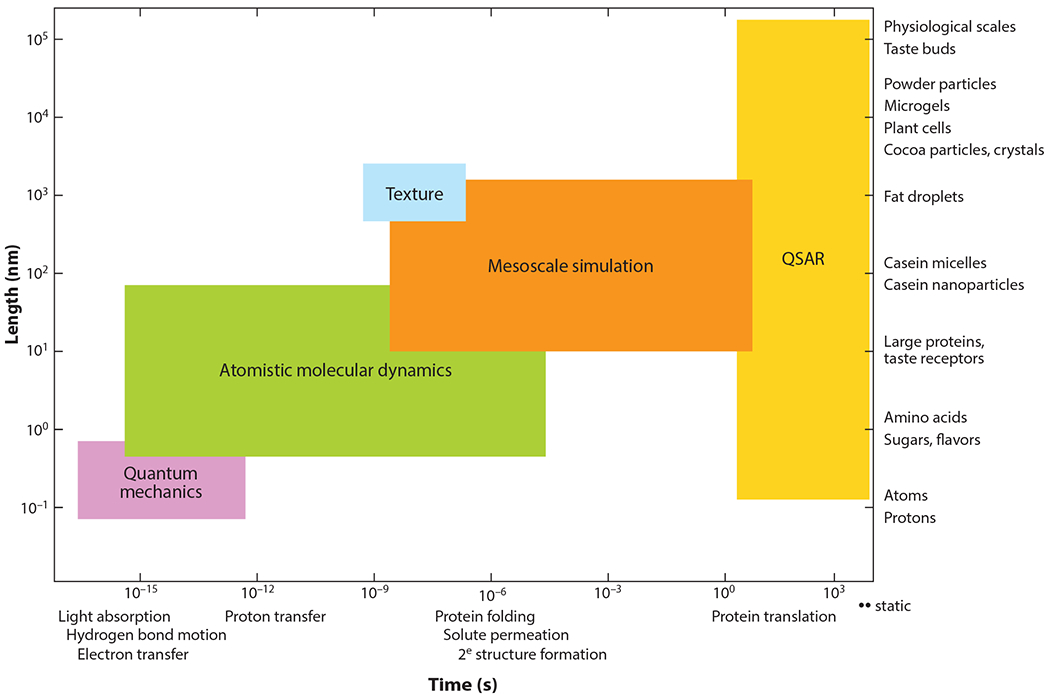
Molecular interactions accounting for food science phenomena across the length scale and timescale and appropriate particle-based simulation methods bridged by quality structure–activity relationships (QSARs).

Multiscale Approach to Modeling Food Assembly and Disassembly

A key aspect of this approach is the identification of corresponding length scales and timescales (Figure 1). Small changes at the molecular level can induce dramatic structural changes with repercussions from the mesoscale to the macroscale. Consider ice cream as an example. It starts as an oil-in-water emulsion that is frozen while incorporating air to produce a final structure with water and sugar crystals dispersed in a mixed emulsion/foam structure. The folding and unfolding of proteins at the oil–water interface during this process occur at nanometer scales, whereas the creation and cleavage of disulfide bonds entailed in protein adsorption at the surface occur on Ångstrom scales. Altering the protein state or solvent environment (e.g., pH or mineral content) can result in dramatic changes in protein conformation and folding at the emulsion interface. This in turn may lead to large changes in ice cream macroscale appearance, stability, rheology, and mouthfeel. Another example relates to how aroma and taste compounds are perceived. One needs to consider the breakdown of mesoscopic and macroscopic food structural elements by mastication and how that controls nanoscale interaction between food tastant and neuroreceptors at the tongue surface. The digestion of the food bolus as it passes through the gut is another example of a multiscale phenomenon, from the physical breakdown of a macroscale bolus to the mesoscale reorganization of fat globules with bile salts or protein hydrolysis by specific digestive enzymes and the molecular-scale transport of nutrients across the gut membrane.

Although a solely multiscale simulation approach to predict the properties of food products with specific appearance, taste, and nutritive quality is feasible in principle, in practice the sheer complexity of food renders such an approach unrealistic. However, multiscale approaches combined with data from, for example, human tasters and statistical and machine learning methods, such as quantitative structure–activity relationships (QSARs) and quantitative structure–property relationships (QSPRs), can connect the molecular scale with physiological outcomes (Roy et al. 2015) and perceptions of taste (Kier 1972, Shallenberger & Acree 1967). Similar approaches are used in biomedical contexts, such as relating the multiscale properties of nanomaterials to physiological outcomes in toxicology (Kar & Leszczynski 2019).

In Silico Approaches

Particle-based simulation of soft matter using supercomputers can be used to explore the phenomena and length scales of interest. In this context, the notion of a particle depends on the simulation method(s) and models appropriate to each length scale and process as follows.

Mesoscale properties of food colloids, such as sols, foams, emulsions, and gels, can be explored using coarse-grained (CG), particle-based simulations, in which each particle may represent a few atoms [such as each individual amino acid (AA)] to hundreds of AAs (such as globular proteins treated as rigid bodies). CG models bring simulations closer to experimentally accessible temporal and spatial scales, provided that the dimensionality reduction does not entail the loss of a key detail or underlying mechanism. In particular, food rheology and microstructure can be conveniently studied at the mesoscale level. Simulations can address, for example, the coalescence of emulsion droplets and the influence of adsorbing amphiphilic molecules on these processes (Morris & Grove 2013, Pink & Razul 2014) and the phase behavior of microemulsions, and provide data on interfacial tension and morphology of the mesoscopic aggregates (Liu et al. 2015) and molecular adsorption at interfaces.

Molecular processes such as the unfolding or denaturation of proteins occurring in thermal processing or the noncovalent binding of tastants to receptors in the tongue can be explored using classical molecular dynamics (MD), where particles represent individual atoms and the relevant length scales are Ångstroms. For example, the binding of ligands to sweet or bitter taste receptors can trigger conformational changes and downstream chemical/molecular signaling that eventually lead to taste perception. Molecular-level modifications of the tastant can greatly affect such perceptions.

At even finer length scales the particles may be electrons, protons, and nuclei, and a paradigm shift of physical method to elucidate the phenomena is required, as quantum-mechanical (QM) effects may occur. These include the creation and cleavage of covalent bonds in the hydrolysis of sugars, fats, and proteins and the Maillard browning reaction between AAs and reducing sugars that gives many foods their distinctive colors and flavors. It can also be used to determine the protonation and deprotonation of titratable sites of proteins during food processing and digestion. Hybrid approaches are also possible, such as QM/MD (Bolnykh et al. 2019, Guest 2012) or CG/MD, which combine a fine-scale level of description with a much coarser one.

• As one might expect, as particle size is reduced, the number of particles needed to simulate a complex system increases, as does the computational cost of the simulation. Consider the ubiquitous example of pH regulation of protein aggregation. As pH changes, protons transfer from solvent to acidic or basic titratable sites, but this can also allow proteins to fold. Thus, many different length scales may be involved. Quantum mechanics is in principle relevant, but often approximations are necessary. MD is much more suited to modeling protein folding, and for large protein complexes, mesoscale modeling is often more useful. At the densities typical of food complexes, MD is usually the most efficient means to perform realistic simulations. An MD simulation involves numerically integrating Newton’s equation of motion over typically millions to billions of small time-steps. For this, the forces on the particles (typically atoms) of the system must be known. In biology (and therefore food science), the most frequently used models for interatomic forces, called force fields (FFs), include CHARMM (MacKerell 2004, MacKerell et al. 1998) and Amber (Ponder & Case 2003). Depending on the system, Monte Carlo (MC) methods (Binder 1997, Frenkel et al. 2001) can often provide a more efficient means to simulate equilibrium properties of biophysical systems, particularly when water can be treated implicitly. Unlike MD, MC simulation only requires total energies of a system and is free to move particles in ways that may appear unphysical, provided they are consistent with the system’s thermodynamic constraints.

• The food scientist armed with suitable simulation methods also has to address the issue of timescales. This issue can be appreciated using the example of the folding or unfolding of food proteins, which may take place during drying or hydration of food and for which classical MD is appropriate. In this case, the smallest timescale, associated with the vibrations of bonds involving hydrogen, is on the order of femtoseconds and determines the size of the simulation-integrating time-step. However, the timescales associated with folding or complex formation can be on the order of milliseconds or even seconds. A host of statistical sampling techniques known as rare-event methods exist to address problems involving such different timescales, whether the simulation method used is quantum, classical, or mesoscale. They surmount the rare-event problem through the application of biasing forces or energies to place the system in configurations where such events are likely and then correct mathematically for the effects of the bias. This requires a set of order parameters that determine the locations of such events. When the number of order parameters is no more than three or so, a variety of statistical techniques can be used to build the corresponding free-energy surface. One such technique is well-tempered metadynamics (Barducci et al. 2008). When the number of order parameters is large, a method known as temperature-accelerated MD (TAMD) (Abrams & Vanden-Eijnden 2010) may be appropriate. This method couples the order parameters to a hot thermostat to pull the system out of free-energy wells where it might otherwise be stuck. Another approach that can be combined with experimental data having molecular resolution, such as nuclear magnetic resonance (NMR), is steered MD, which dynamically guides the system to the regions that need to be sampled. Several sophisticated algorithms, such as the String method (Maragliano et al. 2006, Vanden-Eijnden & Venturoli 2009), also exist to find the most likely reaction path of thermodynamic processes. An important and complementary methodology comes from computer science: Machine learning is increasingly being combined with particle-based simulation at all the above length scales. Not only is it facilitating the modeling of complex phenomena themselves but, in some cases, allows particle-based properties to be related to physiological outcomes such as toxicity or perception of taste as expressed by panels of human tasters.

Quantitative Structure–Activity Relationships and Physiological Models for Predicting Complex Functionalities

The molecular-level interactions that determine food component association, transport, and absorption at long timescales are complex and difficult to model in full detail. An increasingly viable alternative is to relate molecular features to the specific functionality, such as taste, using QSARs. QSARs are analytical expressions representing correlations between the activity of a substance and quantitative chemical attributes representing the molecular features of the substance (Roy et al. 2015). The term QSPR is also used. QSARs and QSPRs are often developed using statistical techniques, with some modern QSARs/QSPRs being derived using machine learning methods. The features that can serve as inputs to QSAR/QSPR models range from very simple zero-dimensional (0D) features, such as those based on the empirical chemical formula (e.g., number of atoms, number of bonds, molecular weight), all the way to 7D features involving real target-based receptor model data (Kar & Leszczynski 2019, Roy et al. 2015). The increasing feature dimensionality is a measure of the complexity of the data required (see Figure 2). For example, 1D features involve information based on the chemical fragments that make up the molecule (similar to classical group-contribution methods), 2D features include information based on the molecular connectivity, 3D methods use information based on the three-dimensional structure of the molecule, and descriptors beyond 3D use more complex information such as sets of molecular conformations, solvation, protonation states, and even models containing information about the biological targets involved. Other descriptors used in describing molecule reactivity, or adsorption on solid surfaces or interfaces, include the electronic properties (highest occupied/lowest unoccupied molecular orbitals, polarizability), charge, van der Waals (VDW) surface energy, or binding energies of selected sets of representative molecule fragments. These have been used to predict nanoparticle (NP) cell uptake and toxicity (Kamath et al. 2015, Liu et al. 2015, Xia et al. 2011).

Figure 2.

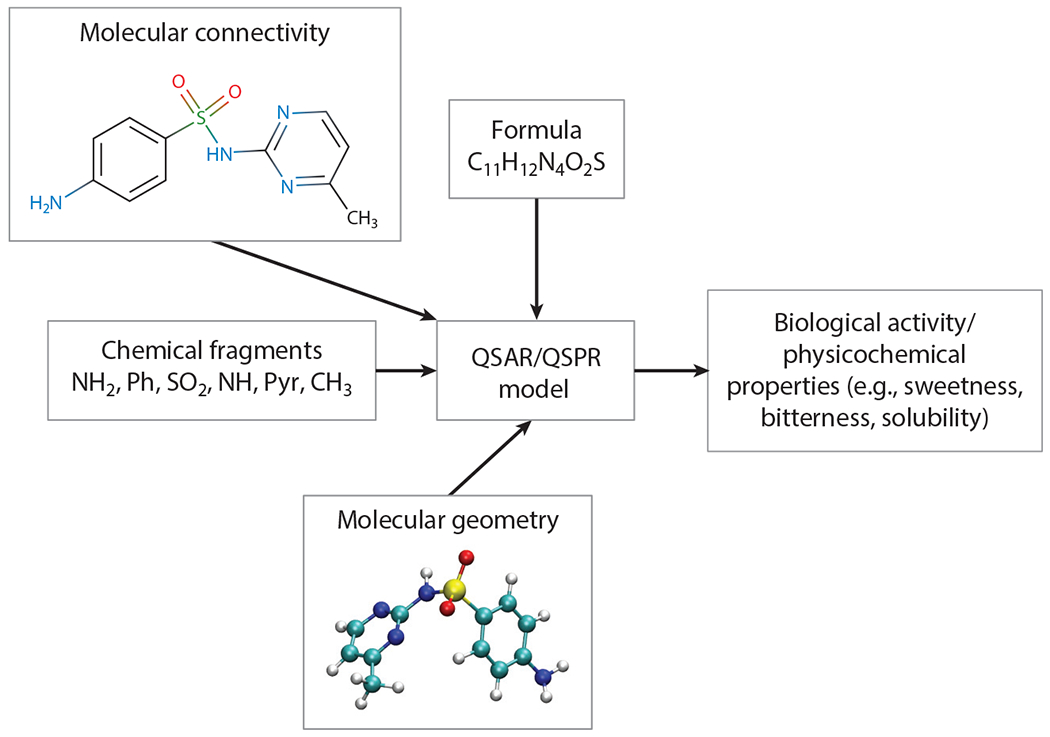
A schematic showing some of the types of molecular descriptors, such as molecular connectivity, formula, geometry, chemical fragments, physicochemical properties, and biological activity, that can be used to fit a quantitative structure–activity relationship (QSAR)/quantitative structure–property relationship (QSPR) model to make predictions.

This article is intended as an overview of the possibilities of particle-based simulation and its combination with the QSAR/QSPR models to address problems in food science. We review the simulation toolbox for the food scientist and briefly describe particle simulation methods along with the most popular and potent open-source, freely available software packages. These methodologies are illustrated with representative cutting-edge examples. We conclude our discussion by surveying some of the current challenges for particle-based simulation in food science.

MOLECULAR SIMULATION TOOLBOX FOR FOOD SCIENTISTS

The previous discussion has summarized how different simulation methods can help address problems involving different length scales and timescales within food science and how they can be augmented/complemented by QSAR/QSPR models. In practice, simulating systems consisting of hundreds, thousands, or even millions of particles for a billion time-steps is daunting. Although the brave may choose to develop their own in-house simulation engines, most users and, indeed, developers rely on free, community-developed software packages, which are becoming increasingly user-friendly and adaptable, including the Groningen Machine for Chemical Simulations (GROMACS) (Berendsen et al. 1995, Pronk et al. 2013), Amber (Case et al. 2005, Salomon-Ferrer et al. 2013), Open Molecular Mechanics (OpenMM) (Eastman et al. 2017), Nanoscale Molecular Dynamics (NAMD) (Phillips et al. 2005), and the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (Plimpton 1995). All of these can run on hardware ranging from good laptops to massively parallel supercomputers. The first four engines are used primarily for biosystems and include tools to facilitate biosystem preparation, simulation, and analysis. LAMMPS, although capable of simulating biosystems, is more often used for advanced materials and, recently, even quantum problems in the context of machine learning. All are capable of simulating both thermodynamic equilibrium properties (i.e., free-energy properties) and dynamical/kinetic properties. Most of the MD engines mentioned above are also capable of running CG and MC simulations. In addition, several other engines have been built specifically for CG and multiscale/hybrid simulations, including Espresso (Weik et al. 2019) and the Daresbury Labs mesoscale simulation package (DL-MESO). Hybrid molecular CG schemes have also been developed (Krekeler et al. 2018, Tarenzi et al. 2019) in which critically important fine-scale details are treated atomistically, with all other features treated at a CG or even continuum level. Many MD engines include rare-event software and can also be interfaced with software such as the Plugin for Molecular Dynamics (PLUMED) developed specifically for rare-event methods (Bonomi et al. 2009). In addition to their use for characterizing thermodynamic equilibrium properties, rare-event methods can be used for kinetics such as estimating reaction and nucleation rates (Casasnovas et al. 2017, Swenson et al. 2019).

The power of simulation to investigate the molecular and mesoscale mechanisms taking place in food materials is best shown through practical examples. As a first example, consider the case of pH-controlled immobilization and release of biomolecules.

pH-Controlled Immobilization and Release of Biomolecules in Whey Protein Isolate–Based Microgels

Whey protein isolate (WPI) can be formed into microgels used as matrices to immobilize and release a variety of bioactives. These mesoscale structures can function as smart delivery systems in which uptake and release of bioactives are facilitated by environmental pH changes (Egan et al. 2014). A semiempirical analytical model to predict the conditions of attractive and repulsive interactions between the constituents of the microgel–bioactives complex can be made based on the electrostatic charge expected for each constituent given their pKa values and the solution pH. Although uptake by these microgels of single AAs (histidine, arginine, and lysine) was adequately described by this simple model, interactions with either cationic KHIQK or anionic WENGE peptides were only partially described. In particular, although the maximum experimental interaction is well predicted, some attractive interaction is observed when both WPI microgel and peptide carry a similar net charge, in sharp contradiction with Coulomb’s law. This attraction on the wrong side of the isoelectric point (pi) has been reported for other experimental systems, such as quinoa proteins–carrageenan (Montellano et al. 2018).

Simulations can improve our ability to control and release bioactives from microgels, or any microencapsulation process, in several ways. First, predicting the pKa value of large proteins can be extremely difficult experimentally, particularly if they can fold/unfold as solution conditions change. Second, important interactions take place through different electrostatic mechanisms, such as charge fluctuation (Barroso da Silva & Jönsson 2009; Barroso da Silva et al. 2006, 2014; Jönsson et al. 2007) and dipole interactions (Barroso da Silva et al. 2016), that are difficult to elucidate experimentally. Conversely, molecular simulation methods that incorporate pH effects can address these problems, including the puzzle of complexation on the wrong side of pI (Barroso da Silva & Dias 2017, Barroso da Silva et al. 2019, Chen et al. 2014), in good agreement with experiment.

The first few steps of simulation.

The first step of a simulation is preparing its initial conditions. For simulations at the molecular level, the best initial structures are usually experimentally determined, either by X-ray or NMR, and are available in the Protein Data Bank (PDB) (Berman et al. 2014). When experimental structural information is lacking, estimates can often be obtained using bioinformatics, usually through homology modeling (Leach 1996) or machine learning applied to PDB libraries, to statistically predict likely structures employing software/servers such as I-TASSER (Yang et al. 2014), SWISS-MODEL (Biasini et al. 2014), and INTFOLD (McGuffin et al. 2019). Large proteins and protein adducts are generally too complex to predict using bioinformatics in isolation, but they can often be built from smaller ones predicted from bioinformatics. These are then stitched (i.e., bonded) together using homology tools such as Modeller (https://salilab.org/modeller/), although the task of determining the native structure can be very complex. For example, beta-lactoglobulin (β-lac), a milk protein, consists of 160 AAs, each comprising some 20 atoms, and is already too complex to be realistically simulated from arbitrary initial configurations.

The second step involves adjusting components of the complex, such as the inclusion of counterions, solvation, and protonation/deprotonation of titratable sites [constant-charge or constant-pH (CpH) approach (Barroso da Silva & Dias 2017)]. Also needed for a more realistic description of the real systems is the possible creation of bonds that may exist within and between proteins, such as between cysteine residues in the case of WPI microgels or between glycans and proteins. Although it is often difficult to know which titratable sites should be protonated or deprotonated, or where bonds should be created or broken, powerful user-friendly software tools to make such changes are available for constant-charge simulations, including PROPKA (Olsson et al. 2011) and/or the CHARMM-GUI (Jo et al. 2008).

The third step is the actual simulation of the complex. Molecular simulations require interaction energy models (FFs), as mentioned above (see also van Gunsteren & Berendsen 1990, Leach 1996, Schlick 2010), and suitable molecular simulation software. In some instances, steps 2 and 3 can be intertwined, as illustrated below.

Constant-pH simulation methods for food proteins.

Predicting molecular-level changes to protein complexes or other macromolecules occurring as pH and salt concentration change can be extremely difficult, from both experimental and simulation/theoretical perspectives, as the binding/unbinding and transport of protons between titratable sites are fundamentally quantum effects. Even assuming that these effects can be adequately modeled considering only the quantum ground state, a realistic quantum simulation can handle at most a tiny peptide consisting of 1–3 residues together with water and relevant ions (such as Na⁺, K⁺, Cl⁻). Because proteins of interest are generally far larger, a wide variety of approximate simulation methods have been developed over the past two decades to describe their molecular properties and the conditions that control their aggregation as complexes. A great variety of CpH simulation methods are available to study biomolecular phenomena (Barroso da Silva & Dias 2017; Barroso da Silva & MacKernan 2017; Barroso da Silva et al. 2019; Bennett et al. 2013; Chen & Roux 2015; Delboni & Barroso da Silva 2016; Donnini et al. 2016, 2011). Here, we describe two methods that involve different CG levels. In both methods, each titratable site is either an acid or a base. In the absence of interactions between sites, the probability of a site being deprotonated or protonated is entirely determined by the pKa value of the isolated site and the pH of the solvent. In reality, titratable sites interact primarily through Coulomb interactions and are affected by all other charges. In the first approach, a mesoscale semiempirical description, several physical chemistry features are considered, including the empirical pKa values of the isolated sites (usually pKa values of the free AA in solution), the charges due to possible transfers of protons to/from sites, the location of sites, the salt concentration (treated implicitly), the temperature, and, as a phenomenological parameter, the solution pH (Barroso da Silva et al. 2006, Srivastava et al. 2017, Teixeira et al. 2010). The second approach, known as CpH MD simulations, uses a finer level of description in which the partial charges and dynamical/instantaneous positions of each atom are considered. The approach uses an atomistic representation of water, added salt, protons, and counterions, ensuring that the system remains charge neutral overall (Donnini et al. 2016, 2011).

Although the two approaches have certain similarities, in practice they are very different. The statistics for the first approach are generated through MC sampling and, unlike the second, cannot account for structural changes such as protein folding/unfolding, because of the use of a fixed protein structure. However, it has three distinct advantages. First, empirical data can be easily incorporated; second, the system size that can be investigated is very large; and third, the convergence rate of sampling can be rapid, enabling the calculation of interaction free energies at different experimental conditions (Srivastava et al. 2017). Furthermore, notwithstanding its simplicity, it turns out to be surprisingly accurate for several (but not all) proteins, RNA, and DNA systems (Barroso da Silva & Dias 2017, Barroso da Silva & MacKernan 2017).

The second approach has a distinct advantage over the first when working with flexible macromolecules. An example is the implementation of a CpH MD (Donnini et al. 2011, 2016) based on the λ-dynamics approach (Kong & Brooks 1996, Lee et al. 2004). The protonation coordinate (λ) is a continuous degree of freedom, varying between 0 (protonated site) and 1 (deprotonated site). λ can be imagined as a particle that is incorporated in the interaction potential of the system and fluctuates between the protonation states of a site. The pH dependency of protonation/deprotonation is included in the potential function using a phenomenological description dependent on the experimentally determined pKa values of the isolated sites. At each step during the simulation, the force acting on λ is computed as it is for other particles in the system. The coupling of sites is directly accounted for through the potential energy of the system.

In this approach, protons are not modeled explicitly. Therefore, when the protonation state of a site changes, the total charge of the system (protein and solvent) changes as well, and the system is no longer neutral. Because this may lead to artifacts in MD simulations (Hub et al. 2014), protonation of a site on the protein is usually coupled to deprotonation of a counterion in solution (Chen & Roux 2015, Chen et al. 2013, Dobrev et al. 2017). Such an approach becomes laborious when the number of titratable sites is large. In proteins with many sites, however, the fluctuation of the overall protein charge is typically much smaller than the number of titratable sites. Therefore, a small proton buffer can be introduced such that a change in the total number of protons of the protein is compensated by an opposite change in the number of protons in the buffer. This reduces the computational effort without affecting the relative free energies of the different charge states. Successful examples of applications can be found in the literature (Bennett et al. 2013, Donnini et al. 2016).

Taste Receptors and Glycophores

One key molecular event contributing to consumers’ likes and dislikes of foods is the interaction between tastants and their target receptors in the tongue. Taste, combined with the other senses of smell, sight, hearing, and touch (texture), provides an overall sensory evaluation of food. In addition, bitter taste receptors have also been found elsewhere in the human body, for example, in the palate, brain, upper esophagus, and larynx, and are associated with a variety of diseases (Alfonso-Prieto et al. 2019). The five basic tastes salty, sweet, bitter, sour, and umami are sensed through different receptors. Ion channels are responsible for the perception of saltiness, whereas the nature of the receptors for sour tastants is still an object of debate. G-protein-coupled receptors (GPCRs) detect sweet, bitter, and umami. GPCRs are transmembrane proteins composing three domains: the extracellular domain (ECD), which is outside the cell (ligands such as tastants or odorants bind to it); the transverse membrane domain (TMD); and the intracellular domain (ICD), to which cognate G-proteins are attached. Agonist ligands (e.g., tastants) binding to the receptor result in conformational changes that may lead to release from the ICD of parts of the G-protein, leading to a complex set of downstream intracellular signaling events. As GPCRs function at a molecular level, simulation can be used to reveal aspects of structure and function and facilitate the development of new tastants.

The main preparatory steps required for such a simulation are the same as those described for WPI microgels. However, additional steps are often required to prepare a detailed taste-receptor system, as accurate information regarding the 3D structure for most human GPCRs (hGPCRs) is unfortunately lacking. This is the case for some 400 receptors involved in chemical sensing, representing about half of all hGPCRs, and includes those devoted to taste and smell sensing. Bioinformatics predictions are poor here because of the lack of good templates, as applying X-ray crystallography to transmembrane proteins is challenging (Fierro et al. 2017).

A receptor model may be built by stitching together the ECD, TMD, and ICD using homology modeling software such as Modeller, with individual domains extracted from either PDB, or using bioinformatics tools mentioned above (see Figures 3 and 4 for illustrations). Although some G-protein-coupled taste receptors function as monomers (e.g., for bitterness), others may function as dimers, and for such cases (Hiller et al. 2013) the corresponding GPCR pair may need to flank each other. Next, the membrane–GPCR complex must be built. The membrane is usually modeled as a lipid bilayer created with hundreds of lipid molecules, which must be appropriately placed about the transcellular domain of the GPCR dimer (or oligomer). Various packages, for example, Membrane Builder, are available to build protein membrane complexes (Wu et al. 2014). Third, water and salt at physiological levels are added and the protonation state of each residue is suitably adjusted using, for example, the PROPKA server (Rostkowski et al. 2011). After these steps, the receptor complex typically contains some 500 residues, a lipid bilayer, water, and salts, amounting to more than 200,000 atoms.

Figure 3.

Multiscale hybrid molecular mechanics (MM)/coarse-grained (CG) simulation approach for human G-protein-coupled receptors (hGPCRs). Here, a fine level of detail is retained for the binding region of the receptor and a coarser level of detail is used for the rest of the system. Figure courtesy of Ksenia Korshunova.

Figure 4.

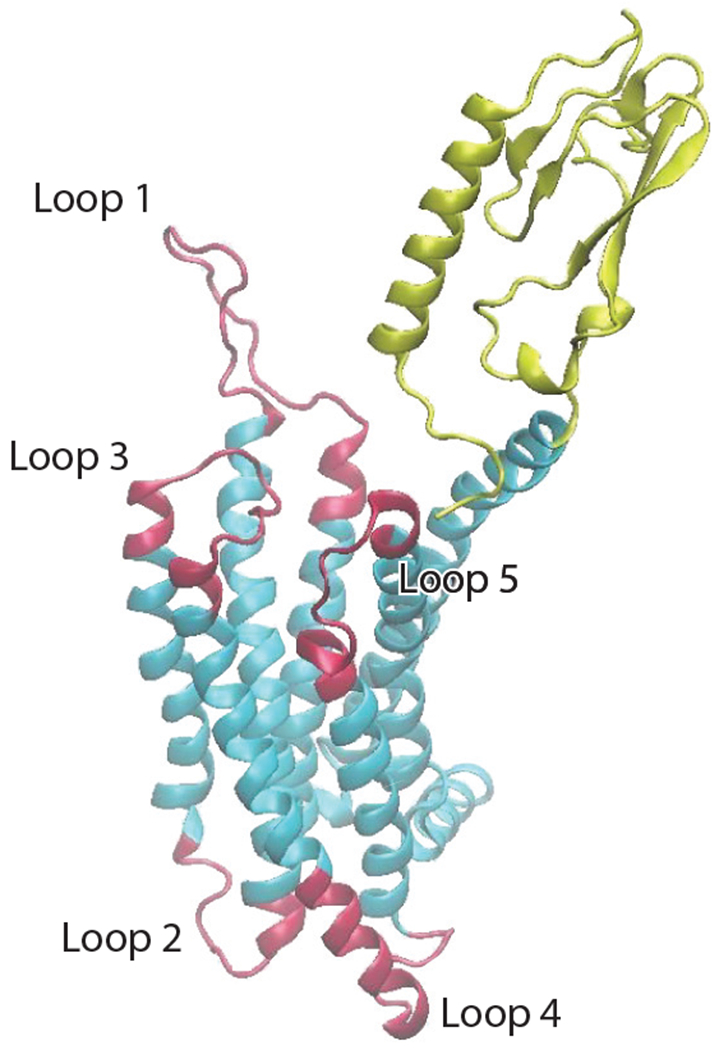
The graphic representation of the GLP-1R (glucagon-like peptide-1 receptor). The red loops are accelerated by temperature-accelerated molecular dynamics. In addition to the loops, the mass center of the extracellular domain (ECD) is accelerated (yellow region), the intracellular domain (ICD) is the lower part of the protein in the vicinity of and including loops 2 and 4, and the transverse membrane domain lies between the ECD and ICD. The lipid membrane, water, and salt ions are not rendered for clarity.

The next step is usually determining the equilibrium structure(s) of the GPCR complex, which is often very challenging, requiring sophisticated sampling methods and significant computational resources. We should mention, however, that there are ingenious ways to sometimes avoid some or all of the above tasks. One example is based on the fact that the general structure of GPCR proteins is known, and the ICDs are not thought to vary greatly within each GPCR family. Therefore, it can be argued that only the ECD needs to be known accurately, as it provides the binding sites for ligands and is typically much more variable than the other domains. Following this logic, one can use bioinformatics and multiscale simulation to predict the pose of bitter taste receptors’ agonists.

Alternatively, a multiscale, hybrid molecular mechanics (MM)/CG simulation approach tailored for GPCRs can be used (Alfonso-Prieto et al. 2019, Sandal et al. 2015), which describes explicitly the ligand, its binding site, and a solvation sphere, as illustrated in Figure 3. The rest of the protein and the bulk solvent are included using a simplified CG representation (Tarenzi et al. 2019, 2017). The method allows for sampling of longer timescales, crucial for GPCR homology models with low sequence identity with the template (Rayan 2010).

Probing the structure of G-protein-coupled receptors close to equilibrium.

As discussed above, rare-event methods can be used to explore relevant conformations of the GPCR complex close to and at equilibrium through the application of artificial biasing forces, provided suitable order parameters are known. As an example, consider a complex consisting of two β-lac molecules in water and salt. Depending on the solvent conditions, the pair may bind together or may dissociate. The simplest order parameter to characterize this would be the distance between the centers of mass of the proteins, but others describing, for instance, the solvent structure in the vicinity of the pair may be needed to fully characterize the dissociation process. Identifying suitable order parameters for GPCR proteins is more difficult, as illustrated by a representative and important example, GPL-1R (see Figure 4), which is involved in the control of blood sugar via secretion of insulin. Patients with type 2 diabetes have a reduced ability to produce GLP-1, and its administration to patients is not practical because of its very short half-life in the body. GLP-1 analogs with much longer lifetimes are currently used in treatment, but there are concerns that most effective ones may be carcinogenic. Interestingly, experimental findings from food and health sciences indicate that certain milk peptides may also act as GLP-1 analogs, but to be exploitable further confirmatory evidence is needed at a molecular level. Acquiring confirmatory evidence requires representative structures of the receptor that are close to equilibrium, which first entailed building the GPCR complex as described above.

As these are expected to be associated with very flexible regions of the receptor, we used TAMD applied to the most flexible regions (mass centers of five loops and the ECD) of the receptor (see Figure 4) and a schedule of heating and cooling of the TAMD temperature to drive the receptor to low-energy conformations (Lucid et al. 2013) and collect a very large number of representative snapshots of the complex. This data, in turn, allowed us to perform a demixed principal component analysis (DPCA) of the motion of dihedral angles of the protein backbone to extract the dominant (slowest) modes of DPCA, which were, in turn, used to estimate the corresponding free energy surface and the slowest dynamical modes of the receptor.

Glycophores and sweet taste.

A useful QSAR to study taste perception is the glycophore theory. The perception of sweetness involves complex molecular interactions between foods and taste receptors in the tongue. Nevertheless, there are known chemical motifs that lead to sweet taste, or glycophores. In 1967, Shallenberger & Acree (1967), introduced the AH-B theory of sweetness, an early QSAR positing that sweet taste results from a basic structural unit common to all sweet molecules. The unit consists of two electronegative atoms, A and B, one of which (A) has a hydrogen atom attached to it. AH is therefore a proton donor and B a proton acceptor. This theory was later refined by Kier (1972), who observed that a third, polarizable moiety X should also be present to produce a sweet taste. Glycophores provide a quick but powerful route to assess sweetness at the molecular scale without the need for dealing explicitly with taste receptors and can be used in combination with enhanced sampling and machine learning techniques to discover new sweeteners. In the language of descriptor dimensionality discussed above, this would be an example of a 3D descriptor.

The glycophore theory has been a powerful tool to understand sweet taste behavior, even in complex systems. A recent example is the work of Chopade et al. (2015) investigating the unusual behavior of the steviol glycoside rebaudioside-A (Reb-A), a high-potency noncaloric sweetener extracted from the leaves of Stevia rebaudiana. Reb-A exhibits a nonmonotonic dependence of sweetness with temperature, with maximum sweetness close to 0°C and minimum around 40°C, beyond which sweetness increases again. The work combined 2D NMR techniques and steered MD simulations, in conjunction with the glycophore theory, to show that changes in intramolecular hydrogen bonding patterns with temperature result in different numbers of AH-B-X motifs being presented by Reb-A in solution, following the same trend observed in taste panels with temperature (Figure 5). This illustrates the power of combining molecular simulation, QSPR models, and experiments to link taste perception to the molecular physics of sweet molecules.

Figure 5.

Snapshots from molecular dynamics simulations of rebaudioside-A, highlighting AH-B-X motifs presented at different temperatures. Motif 1 only appears at low temperature, whereas motif 2 is present at low and high temperatures, but not at the sweetness minimum.

Protein-Interface Interactions and Nanoparticle Uptake

Liquid and gel-like foods as well as pharmaceutical products use protein-based emulsions (Ubbink 2012), in which proteins provide a biocompatible, stabilizing coating and the core can be used to encapsulate bioactive components. The behavior of these systems is determined in part by the properties of the stabilizing interfacial film. Understanding protein structure at liquid interfaces is key for controlling emulsion formation (He et al. 2013) and stabilizing the dispersed phase against flocculation and coalescence. In food processing, molecular adsorption and fouling on equipment can cause major problems, particularly in the dairy industry (Wilson 2018). Because of its ability to access length scales characterizing interfacial systems, mesoscale simulation is ideally suited to the study of essential food components at interfaces.

Molecular dynamics investigation of protein behavior at liquid interfaces.

The conformations that proteins adopt at liquid interfaces are a key factor determining the behavior of protein-based emulsions. Adsorption on interfaces affects the conformation, as hydrophobic AAs normally residing in the protein core partition into the hydrophobic medium. The resulting protein conformations determine their interfacial aggregation and assembly. To test the ability of molecular simulation to investigate protein structure at liquid interfaces, recent work studied the conformations of two peptides derived from myoglobin (PDB_ID 1MBN) at the air–water interface (Cheung 2016). Previous experimental work (Poon et al. 1999) showed that one of these peptides, consisting of the first 55 residues of myoglobin, was an effective emulsifier, whereas the other (residues 56–131) was less effective. MD simulation with GROMACS, using replica exchange and solute tempering to enhance conformational sampling in pure water at 25°C, showed that these two peptides adopt various different conformations at the air–water interface. Peptide 1–55 preferentially adopts extended conformations, allowing it to form a well-defined monolayer at the interface. Conversely, peptide 56–131 predominantly adopts compact conformations, which results in a less strongly bound interfacial layer, explaining its lower emulsification ability. Simulations of the globular proteins α-lactalbumin and lysozyme showed similar results (Cheung 2017), with α-lactalbumin (the more effective emulsifier) more frequently adopting extended states.

Another factor determining the behavior of proteins at interfaces is their interfacial adsorption strength. Simulation has been used to determine the adsorption strengths of the hydrophobins HFBI and HFBII at water–octane interfaces (Cheung 2012). The adsorption free energy for the hydrophobins was calculated using steered MD with LAMMPS (Plimpton 1995). This showed that the adsorption free energy was on the order of 10²–10³ kJ/mol, indicating essentially irreversible adsorption. These proteins have similar sequences and solution structures but show different characters (HFBII being slightly hydrophilic and HFBI slightly hydrophobic). Like most hydrophobins, these proteins have a large hydrophobic patch on their surface. To determine the effect of this patch on their interfacial behavior, simulations of HFBII pseudo-proteins with identical interactions (either hydrophilic, hydrophobic, or average) between all protein residues and both solvents were performed. Uniformly hydrophilic and hydrophobic pseudo-proteins preferentially resided in the water and octane phases, respectively. The average protein, however, was surface active but slightly hydrophobic, contrary to the native protein.

Protein–solid surface interactions.

In food processing equipment, adsorbed proteins may create an insulating layer between the heater and the bulk material, reducing the heating efficiency (Bansal et al. 2006). This leads to inefficient sterilization and pasteurization specifically in milk. Furthermore, in filtration processes, protein aggregates deposited on the surface of the filter can block the flow, thus greatly affecting the filter throughput capacity. Enabling control over these processes requires a quantitative understanding of the interactions between biomolecules and materials used in food processing.

Because of their large molecular size and surface charge, the electrostatic and VDW interactions of proteins with solid surfaces are very strong, with typical adhesion energies of 10²–10³ kJ/mol (Power et al. 2019), thus making the adsorption process practically irreversible. Furthermore, the amount and diversity of adsorbed material prohibit its direct atomistic simulation. In these conditions, the size, shape, dipole, and charge distribution on the protein are the most important parameters determining its ability to stick to the surface. Protein conformations, in contrast, are not expected to strongly affect the binding process.

A wide variety of models have been proposed to describe competitive adsorption of proteins at solid interfaces (Bellion et al. 2008, Lopez et al. 2015, Oberle et al. 2015, Rabe et al. 2011, Vilanova et al. 2016, Vilaseca et al. 2013). The simplest models treat proteins as single spherical beads with sizes reflecting their hydrodynamic radius. Although such models allow easier numerical and analytical solutions, they cannot provide any information on the preferred orientation of the molecule at the surface, which is needed to estimate the amount of adsorbed protein and of the structure of the corona. To achieve higher resolution without making the model too complex, one can use the fact that all proteins contain multiple copies of the same AAs, and multiple lipids contain the same alkyl groups. In this approach, one can precalculate the interactions of each repeat unit with the surface and quickly evaluate the potential energy for the entire protein as a sum of energies of nonbonded (VDW + excluded volume) and electrostatic interactions between the AA and segments of the surface. The outer layer on the solid surface is directly in contact with the solvent, and the interactions with the protein residues must include solvent effects and the chemical composition, charge, and hydrophilicity/hydrophobicity of the substrate. Therefore, the interaction of each residue with the nearest part of the surface should include these details (Brandt et al. 2015). The remaining part of the interaction, from the parts not in direct contact, can be evaluated using mean-field and continuum approaches from colloid science (Power et al. 2019).

Although strong assumptions such as pairwise additivity of the AA-surface potentials may affect the absolute adsorption energies, they are still robust in relative terms and allow for screening thousands of molecules, ranking them on the basis of how strongly they attach to the specific surface. This ranking constitutes a unique fingerprint of the material’s surface, which can be related to its activity toward food components. Using the same bottom-up approach, one can engineer an ultra-CG model [united AA (UAA)] that closely reproduces the total protein–protein interaction energy profiles obtained in the united-atom (UA) model (Power et al. 2020). The UAA model typically requires 5 to 30 UAAs to capture the geometry and reproduce the adsorption characteristics of the original protein. This second coarse graining can be based on the mass distribution in the complete protein and then be optimized by tuning the protein diffusion coefficients to those obtained using the UA model. The interaction potentials with the surface can be derived from the UA interaction map by least-squares minimization of the deviations between the UA and UAA models. The UAA model is then suitable for modeling competitive protein adsorption and formation of the protein corona. Examples of the all-atom, UA, and UAA models for the same protein are shown in Figure 6.

Figure 6.

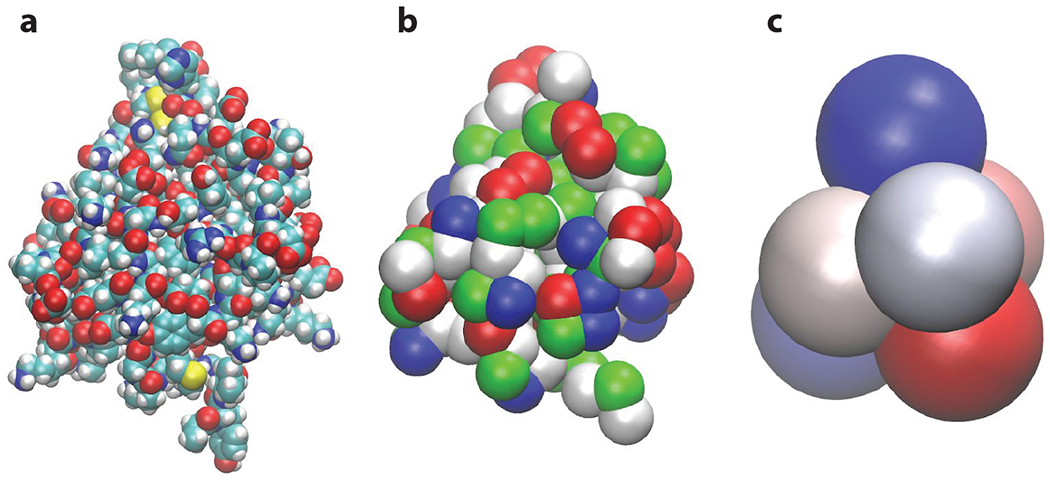
(a) All-atom, (b) united-atom, and (c) united–amino acid representations of bovine β-lactoglobulin A (PDB_ID 1CJ5). The united-atom model is used to model the whole protein adsorption on solid foreign surfaces, while the united–amino acid model is necessary to model competitive adsorption of proteins. In a multiscale modeling framework, each coarse-grained model is parametrized using the more detailed model to preserve their molecular specificity.

Recent studies using this technique have found mean adsorption free energies on metals like gold and silver, as well as on metal oxides of the order of 10²–10³ kJ/mol (Power et al. 2019) for common globular proteins, and were in agreement with the Vroman effect, i.e., the replacement of small and abundant proteins on the surface by larger ones during the competitive adsorption process (Vroman & Adams 1969).

Nanotechnology in food.

Various nanoscale technologies are used to process, package, and enhance food materials (Chellaram et al. 2014). NP additives can be in the form of nanoemulsions for enhanced delivery of nutrients or nanoemulsions to serve as excipients (stabilizers) for longer shelf life and preservation of color, texture, and flavor. One of the primary factors in the design of NPs for food applications is the oral bioavailability (BA) of bioactive compounds in food. There is a need to better understand the fate of bioactive compounds during their passage through the gastrointestinal tract (GIT) to formulate optimal excipient foods to enhance their oral BA. The science behind NP transport through GIT is a multiscale problem. An integrated approach to describe the transport mechanism is to account for the main factors limiting the oral BA of bioactive compounds (He & Hwang 2016, Salvia-Trujillo et al. 2016). The model can be expressed qualitatively through the equation BA = B* A* T*. Here, BA is the oral bioavailability of a particular bioactive compound, B* is the bioaccessibility, A* is the absorption, and T* is the molecular transformation (McClements et al. 2015). While the first two terms, B* and A*, describe the transport and thermodynamic factors in the accessibility and absorption processes, the third factor T* accounts for the fraction present in the active state after any changes in the molecular structure that might have occurred during digestion. Factors determining B*, A*, and T* are governed by the fundamental mechanisms by which NPs interact with human physiology. The mechanisms involve (a) overcoming transport barriers such as through mucus layer, tight junctions between epithelial cells, and bilayer membranes of cells; (b) interaction of NPs with active transporters and cellular efflux pumps; and (c) the transformation of bioactive compounds into more or less active forms because of biochemical or metabolic mechanisms. Analogous multiscale considerations in vascular transport of NPs for drug delivery have been discussed under the umbrella of pharmacokinetic and pharmacodynamic models (Ayyaswamy et al. 2013, Li et al. 2010). As shown in other fields such as drug delivery (Blanco et al. 2015), multiscale modeling (Farokhirad et al. 2017) can serve as a quantitative platform for mechanistic models that account for BA and help guide rational design of NPs in food nanotechnology. Finally, a clearer view of the potential hazards associated with the functionality and applicability of NPs in food is imminently needed to establish regulatory policies on the safety of food nanotechnology (Dimitrijevic et al. 2015, Gallocchio et al. 2015). The progress in the safety assessment of nano-enabled foods can be achieved via knowledge of the relationships between structure and activity of the NPs.

Protein–Sugar Interactions

Two general types of interactions can occur between proteins and saccharides corresponding to the reducing and nonreducing nature of the sugar. The former, essentially the Maillard reaction, starts with a carbonyl (possibly from an aldo or keto sugar) interacting with a primary amine (often from a protein). This covalent interaction starts a cascade of reactions producing, e.g., aroma compounds, reducing compounds, and pigment. Conversely, noncovalent interactions between nonreducing sugars and proteins are involved in phenomena such as those that preserve protein structure under conditions of low water content. In this section, we discuss recent studies on dry heating of dairy proteins, where even residual amounts of reducing sugars can lead to dramatic changes in protein functionality. We then present MD studies exploring noncovalent protein-sugar interactions (specifically trehalose).

Reducing sugar–protein interactions.

As recently reviewed by Guyomarc’h et al. (2015), studies have shown that dry heat–induced denaturation/aggregation of whey proteins results in extensive protein aggregation, with the quality of the final protein ingredient depending on both the extent and size of protein aggregates formed during heat treatment, itself highly sensitive to the physicochemical conditions of the medium and potentially the protein ingredient history. For example, the extent of heat treatment (time and temperature; Norwood et al. 2017), the water activity, and the pH of the powder (Gulzar et al. 2011) all seem to dramatically affect the reaction rate and the nature of the end products formed. In this context, the impact of residual sugars found in protein ingredients has been scarcely investigated. Although industrial WPI have highly variable lactose contents, with most powders containing 2% lactose or less, most concentrates have lactose contents above 3.5%, with a few as high as 10%, and questions remain about the impact of these sugars on the protein aggregation mechanism (Gulzar & Jacquier 2018, Norwood et al. 2017). Although dry heating results in extensive protein aggregation, and the size and stability of aggregates depend on the sugar content and covalent crosslinks (X–X) other than disulfide bonds (S–S), the exact nature of these interactions is not known. This is illustrated in Figure 7.

Figure 7.

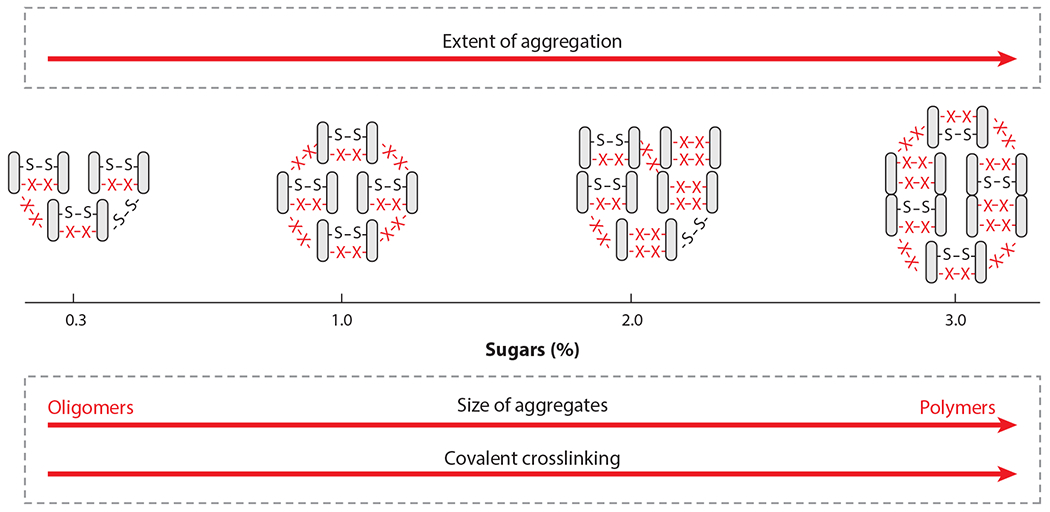
Illustration of the impact of residual sugars on the size and extent of dry heat–induced denaturation/aggregation of whey proteins.

The bond creation and cleavage associated with reducing sugar–protein interactions are QM in nature, yet the computational cost of a quantum simulation of an entire sugar–protein complex is prohibitive. Fortunately, indirect treatments are increasingly possible and include mixed QM/MM approaches (Lu et al. 2016), in which only a small region where quantum effects are important is treated at a quantum level, and the others are treated in the same way as a standard MD.

MD simulations using neural network–based potentials can also simulate large quantum systems (Singraber et al. 2019) but are currently limited to systems having no more than four different atomic species, precluding their use for the Maillard reaction. However, this limitation may soon be overcome. It is also possible to glycolate specific residues within a protein using software such as the CHARMM-GUI (Jo et al. 2008) and explore the properties of the resulting system. Such a pragmatic approach is reasonable when one knows which residues are glycosylated.

The protective effects on proteins of nonreducing disaccharides.

When proteins are embedded in highly concentrated solutions or glassy matrices of nonreducing disaccharides such as sucrose and, in particular, trehalose, they are preserved from damage due to freezing, heating (Ohtake & Wang 2011), or dehydration, resulting in the preservation of coloration and aroma in related products. As a consequence, trehalose is increasingly used in the food industry, pharmaceuticals, and medicine.

Trehalose effectiveness has been related to its high glass-transition temperature (Green & Angell 1989) or to specific interactions with biomolecules involving a substitution or modification of their hydration layers [e.g., water replacement (Carpenter & Crowe 1989) or entrapment (Belton & Gil 1994) hypotheses]. Furthermore, the high viscosity of sugar matrices inhibits large-scale protein motions that lead to structural damage, inactivation, and denaturation (Sampedro & Uribe 2004). The above mechanisms are not mutually exclusive and have been deduced from experimental observations on concentrated solutions or glassy host matrices containing trehalose, sucrose, maltose, and mono- and polysaccharides at different hydrations, temperatures, and compositions (Cordone et al. 2015, Giuffrida et al. 2018). Kinetic and thermodynamic aspects have also been addressed (Semeraro et al. 2017), with the goal of understanding the preserving mechanisms from the atomistic level to the supramolecular and macroscopic levels.

The steps involved in simulating nonreducing sugar–protein complexes in solution are the same as those described in preceding sections. MD simulations have to date provided hints about the effects of trehalose on protein internal dynamics, indicating a key role of residual water on local flexibility. The analysis of solvent partitioning and hydrogen bond (HB) patterns at the protein–solvent interface (Cottone 2007) suggests that preservation effectiveness is mostly due to the sugar’s ability to anchor a thin water layer at the protein surface, preserving the native solvation. Here, water molecules bridge protein and matrix dynamics, reducing protein nonharmonic motions, which results in stabilization of the protein conformation compared to water-solvated systems. However, a few direct protein–trehalose HBs have been detected at very low hydration, allowing visualization of the interchange between water entrapment and water replacement models, depending on hydration. To this end, standard sampling state-of-the-art MD simulations have proven adequate, provided a careful choice of FFs for all the components (Weng et al. 2019).

CONCLUSION AND OUTLOOK

The power of particle-based simulation to elucidate molecular processes taking place in food, from processing and storage to taste, BA, and digestion, has grown dramatically because of improvements in molecular and CG FFs, rare-event methods, mesoscale and multiscale representations, software and methods for system preparation, fast simulation engines that scale extremely well with increasing numbers of computing cores/threads, and inexpensive massively parallel computers. A highly promising development is the emerging hybrid approaches that combine physics-based multiscale materials modeling with statistical modeling (QSARs). These approaches connect advanced molecular descriptors to the functionalities and action of food constituents and thus extend the reach of the traditional schemes. In this context, the role of machine learning is pervasive, ranging from improvements in FFs to the capability to relate atomic or molecular features to physiological effects. Notwithstanding this progress, a number of challenges remain:

• Obtaining equilibrium structures remains very challenging for large or transmembrane proteins even for NMR, X-ray, or cryo-electron microscopy.

• Mesoscale simulations of systems in which conformational changes take place and hydrogen bonding effects are important remain difficult.

• Simulations at constant pH are still challenging, particularly where conformational changes occur.

• Estimating kinetic properties from simulations longer than a millisecond is still challenging, although tremendous progress has been made in the field.

• Simulations of systems far from equilibrium (e.g., systems subject to flow) are difficult to justify theoretically yet important for processing.

• Simulating quantum effects for large biosystems relevant to food science (involving hundreds of AAs) remains a major challenge.

• Organic–inorganic interactions (e.g., protein–metal) are difficult when good FFs are not available.

• Machine learning applications in soft matter are in their infancy, and more work is needed, including systematic dimensionality reduction, a problem shared with order parameters and rare-event methods.

• Simulation is very powerful when combined with sophisticated sampling methods, but these are still very much the domain of experts, and much needs to be done to make them accessible to nonexperts.