Lineage reconstruction from clonal correlations

Significance

Animals begin life as a single cell that divides and differentiates to form a complex body. In doing so, cells make a sequence of fate decisions, often depicted as a tree. A goal in developmental biology is to chart the structure of this tree across tissues, typically by tagging cells and tracking their offspring. Recent advances in DNA sequencing enable tracking thousands of cells simultaneously using unique DNA barcodes, but one can construct false differentiation hierarchies from barcode data. Here, we apply the theory of branching processes to derive conditions under which barcode statistics correctly encode developmental hierarchy. We use this formal basis to develop a practical pipeline for analyzing lineage barcoding experiments. The pipeline is demonstrated in studying hematopoiesis.

Abstract

A central task in developmental biology is to learn the sequence of fate decisions that leads to each mature cell type in a tissue or organism. Recently, clonal labeling of cells using DNA barcodes has emerged as a powerful approach for identifying cells that share a common ancestry of fate decisions. Here we explore the idea that stochasticity of cell fate choice during tissue development could be harnessed to read out lineage relationships after a single step of clonal barcoding. By considering a generalized multitype branching process, we determine the conditions under which the final distribution of barcodes over observed cell types encodes their bona fide lineage relationships. We then propose a method for inferring the order of fate decisions. Our theory predicts a set of symmetries of barcode covariance that serves as a consistency check for the validity of the method. We show that broken symmetries may be used to detect multiple paths of differentiation to the same cell types. We provide computational tools for general use. When applied to barcoding data in hematopoiesis, these tools reconstruct the classical hematopoietic hierarchy and detect couplings between monocytes and dendritic cells and between erythrocytes and basophils that suggest multiple pathways of differentiation for these lineages.

During development and adult tissue turnover, cells differentiate into diverse cell types through a hierarchical sequence of fate choices. The hierarchy can be mapped using lineage tracing, where a tracer molecule or DNA modification is introduced in a group of early cells and then followed over time, allowing identification of the cells’ progeny (1). Recently, advances in DNA sequencing have made it possible to parallelize thousands of lineage tracing assays in a single experiment by labeling cells with unique DNA barcodes (2–4).

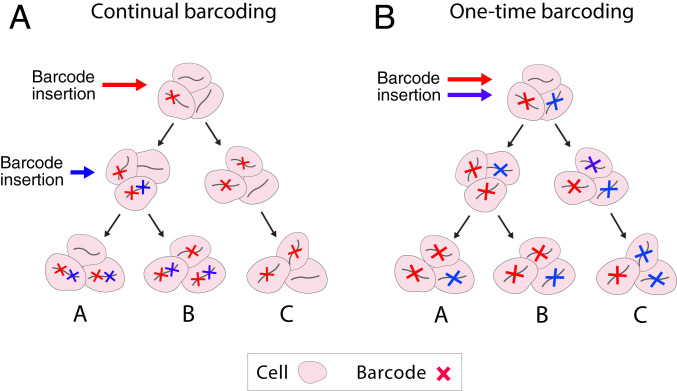
Lineage tracing is carried out through two experimental strategies. “Prospective” lineage tracing seeks to establish the fate of a set of cells that are labeled at an early time point by tracking them to a later time point. “Retrospective” lineage tracing seeks to reconstruct the lineage relationships between cells at a single time point as a way of inferring the history of differentiation branching events that they underwent (5). The usual premise for retrospective lineage reconstruction from barcodes is that two given cell types, “A” and “B,” are more closely related than a third cell type, “C,” when they share barcodes with each other that are not shared with “C” (Fig. 1A) (6). This approach has roots in the tradition of inferring phylogenetic relationships between species based on their common and unique characteristics, such as shared anatomical features or gene sequence alleles that are absent in an outgroup (7).

Fig. 1.

Two principles for inferring developmental hierarchy from lineage tracing barcodes. (A) Barcodes are deposited over time. Multiple insertions in the same lineage of cells create a nested hierarchy of barcoded clones that encode the lineage hierarchy. For example, the blue barcode that is in cell types A and B, but not C, suggests a common progenitor for A and B. (B) Barcodes are deposited all at once. Lineage hierarchy can no longer be inferred from the nesting of barcoded clones but may be encoded in the shared fluctuations of barcode abundance in terminal states. For example, an initial imbalance in the abundance of cells with the red versus blue barcode in the progenitors of A, B, and C manifests eventually in the shared enrichment of red-barcoded cells in A and B.

This phylogenetic approach, however, is limited by the need to accumulate differences in barcodes over a broad developmental window. It is blind to fate choices that occur after barcode diversification has ended. Several experimental methods have now been proposed to continuously barcode cells (8, 9); however, these methods still require optimization to allow uniform rates of long-term barcoding and to analyze tissues with variable rates of division (10). Since most existing methods only label cells within a narrow time window (2, 11–14), it would be useful to develop frameworks for lineage reconstruction beyond the point when barcoding has ended. In a limiting case, one might ask if it is possible to establish retrospective lineage relationships when clonal barcoding occurs just once in a uniform cell population.

Here we explore the idea that stochasticity of cell fate choice in development could be harnessed to infer lineage relationships after barcoding at a single moment in time (Fig. 1B). The intuition is that natural fluctuations between clones in cells entering different lineages would generate statistical signals in the distribution of barcodes over mature cell types and that these statistics alone could report on the lineage hierarchy. Although this phenomenon has not, to our knowledge, been formally described, it may be furnishing some of the signal in existing studies of lineage relationships. Statistical coupling of barcode counts between lineages has been reported using correlation (4, 11, 15), observed/expected ratio (14), Z-score enrichment (16), correlation of Z-score enrichment (13), and other measures. The existence of these couplings is usually attributed to cells being labeled across multiple stages of fate commitment—the phylogenetic approach—but may also arise from stochasticity in cell fate choice.

To explore whether a single step of clonal barcoding could be used to infer lineage hierarchy, it is necessary to model how barcodes partition over time (forward problem) and whether their final statistics encode the tree structure (reverse problem). In the following sections, we define a tree-structured branching process to model the dynamics of clonal expansion and differentiation along a developmental hierarchy. We calculate closed-form expressions for the first- and second-order moments of the clone distributions and report a simple neighbor-joining algorithm that provably reconstructs the hierarchy from a combination of these moments called the normalized covariance. The proof holds under plausible assumptions about the differentiation process. Since the normalized covariance can be easily estimated from barcoding data, this constitutes a practical inference approach.

We also search for self-consistency tests that would fail if our conditions are violated. One of the predictions of our model is that the normalized covariance should obey a set of equalities known as conformal symmetries (17), which can only be broken when one or more of the model assumptions are violated. We investigate one of these violations in detail: the existence of cross-tree transitions where cells differentiate to a final cell type by two alternative paths. There are several notable instances of cross-tree transitions in development, such as neural crest differentiation into mesoderm lineages (18). We formally analyze the types of symmetry violations induced by cross-tree transitions and propose an approach for detecting them in barcoding data.

These results specify a recipe for inferring both cell-type hierarchy and cross-tree transitions that we have implemented as a method called CLiNC (Cell Lineage from Normalized Covariance) available as open source packages in Python and R. We apply CLiNC to a dataset of lineage barcoding in adult mouse hematopoiesis (14) and find that the resulting tree agrees with traditional models of the hematopoietic hierarchy. We also discover a pair of cross-tree transitions that are consistent with recent evidence suggesting multiple pathways of differentiation in the dendritic (19) and myeloid (16, 20–23) lineages. The approaches developed here should provide a mathematical grounding for the interpretation of clonal couplings in other systems.

Results

Generative Model of Differentiation.

We model differentiation as a branching process on a tree. The tree is defined by a set of nodes $T=\left\{0,\dots ,m\right\}$ and a parent function $p:T\to T$ that maps nodes to their parents. We will write $p\left(i\right)\hspace{0.17em}=\hspace{0.17em}j$ when $j$ is the parent of $i$ and use $p^{-1}\left(j\right)$ to denote the children of $j$. In the following, “0” will always refer to the root of the tree and $L\left(T\right)$ to its leaves. Cells at each node pass daughters to their immediate child nodes. The outcome of the differentiation process can be represented as a set of counts $X_i$ recording the number of cells at each node $i$. Our only further assumption is that the process of cell division and differentiation to daughter states is independent and identically distributed for each parental cell. This does not exclude the possibility of cell–cell interactions if these interactions approximate to a mean field. Multiple lineage-tracing studies from developing and adult tissues support the notion that clonal statistics can be well modeled by stochastic processes, even when fate choices are under strong control (24, 25). Under these assumptions, the whole process is governed by the joint distributions $D_i=P\left(X_j,\hspace{0.17em}\hspace{0.17em}j\in p^{-1}\left(i\right)\hspace{0.17em}|\hspace{0.17em}{X}_i=1\right)$ that describe how single cells at each parent node pass daughter cells to the immediate child nodes. The joint distributions, $D$, could encode a wide range of behaviors, including stereotyped or stochastic cell division; strict asymmetric, symmetric, or stochastic daughter fates; fate-dependent division rates; and so on.

Each barcode inserted at the root of $T$ instantiates an independent run of the differentiation process, and the number of cells containing a specific barcode at the leaves of $T$ can be thought of as a sample from the joint distribution $P\left(X_i,\hspace{0.17em}\hspace{0.17em}i\in L\left(T\right)\hspace{0.17em}|\hspace{0.17em}{X}_0=1\right)$. Here, we provide general closed-form expressions for the first- and second-order moments of this distribution and then identify a set of conditions that allows reconstructing the tree from these moments. Complete derivations are available in SI Appendix. Some readers may wish to skip directly to Tree Reconstruction to see how the following mathematical results are put to use.

Calculation of Moments with Probability-Generating Functions.

Directly calculating moments of the barcode distribution is challenging because of the interaction between the division and differentiation distributions at each branch point. These interactions are greatly simplified when the calculation is performed in the domain of probability-generating functions (PGFs). Two properties of PGFs play a key role: (Property 1) nesting of probability distributions in a branching process is represented by function composition in the PGF domain; (Property 2) moments can be calculated as derivatives in the PGF domain. The derivatives of function compositions have a well-understood structure encoded by the chain rule, and this structure scaffolds the moment calculations in our generative model.

The PGF for joint random variables $X_1,\dots ,X_m$ is defined as $G_X\left(z_1,\dots ,z_m\right)=\mathbb{E}\left(z_1^{X_1}\dots \hspace{0.17em}{z}_m^{X_m}\right)$. Let ${\psi }_i$ denote the PGF of $D_i$ and let ${\mathrm{\Psi }}_i$ be the PGF over leaf nodes for the complete subtree rooted at $i$. Our goal is to calculate ${\mathrm{\Psi }}_0$ where 0 is the root of $T$. This is enabled by the following recursion (Property 1), which holds generally for PGFs of nested probability distributions (26):

$${\mathrm{\Psi }}_i={\psi }_i\left({\mathrm{\Psi }}_{j_1},\dots .,{\mathrm{\Psi }}_{j_k}\right)\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}{j}_1,\dots ,j_k\hspace{0.17em}\hspace{0.17em}\text{the}\hspace{0.17em}\text{children}\hspace{0.17em}\text{of}\hspace{0.17em}i.$$

From the PGF, one can calculate moments using the following derivatives (Property 2):

$$\mathbb{E}\left(X_i\right)=\hspace{0.17em}\frac{\partial G_X}{\partial z_i}{\hspace{0.17em}|}_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbb{E}\left(X_i{X}_j\right)=\hspace{0.17em}\frac{{\partial }^2{G}_X}{\partial z_i\partial z_j}{\hspace{0.17em}|}_1,$$

where $1=\left(1,\dots ,1\right).$ To find the moments of the full branching process, we differentiate ${\mathrm{\Psi }}_0$, which requires applying the chain rule to the hierarchically structured composition tree given specified by Property 1. An implication is that the means and covariances of the full branching process depend only on the means and covariances of the local distributions $D_i$. To state this relationship, it helps to introduce notation for the moments of $D_i$:

$$E_i=\hspace{0.17em}\mathbb{E}\left(X_i\hspace{0.17em}|\hspace{0.17em}{X}_{p\left(i\right)}=1\right)$$

$$V_i=\hspace{0.17em}\text{Var}\left(X_i\hspace{0.17em}|\hspace{0.17em}{X}_{p\left(i\right)}=1\right)$$

$$C_{i,j}=\hspace{0.17em}\text{Cov}\left(X_i,X_j\hspace{0.17em}|\hspace{0.17em}{X}_{p\left(i\right)}=1\right),$$

where $C_{i,j}$ is defined for pairs $i,j$ with $p\left(i\right)=p\left(j\right)$.

First-Order Moments.

The first-order moments, $\mathbb{E}\left(X_i\hspace{0.17em}|\hspace{0.17em}{X}_0=1\right)$, can be obtained by applying the chain rule as follows:

$$\mathbb{E}\left(X_i\hspace{0.17em}|\hspace{0.17em}{X}_0=1\right)=\hspace{0.17em}\frac{\partial {\mathrm{\Psi }}_0}{z_i}{\hspace{0.17em}|}_1=\left(\frac{\partial {\psi }_{p\left(i\right)}}{\partial z_i}{\hspace{0.17em}|}_1\right)\left(\frac{\partial {\psi }_{p^2\left(i\right)}}{\partial z_{p\left(i\right)}}{\hspace{0.17em}|}_1\right)\dots \left(\frac{\partial {\psi }_0}{\partial z_{p^{N-1}\left(i\right)}}{\hspace{0.17em}|}_1\right)={\displaystyle \prod _{k=0}^{N-1}{E}_{p^k\left(i\right)}},$$

where N is the number of steps from node i to the root. This calculation shows that the mean number of cells at node i is simply the product of the expected cell growth at each step on the path from the root to i.

Second-Order Moments.

The second-order moments, $\text{Cov}\left(X_i,\hspace{0.17em}{X}_j\hspace{0.17em}|\hspace{0.17em}{X}_0=1\right)$, can be calculated by a similar principle, applying the chain rule to the second derivatives of ${\mathrm{\Psi }}_0$ (SI Appendix). The key result (Theorem 2) is stated here. For any pair of leaves $i,j$, if M is the distance to their most recent common ancestor [i.e., M is the minimal integer satisfying $p^M\left(i\right)=p^M\left(j\right)$], then

$$\frac{\text{Cov}\left(X_i,\hspace{0.17em}{X}_j\right)}{\mathbb{E}\left(X_i\right)\mathbb{E}\left(X_j\right)}={\displaystyle \sum _{m=M}^{N-1}\frac{1}{\mathbb{E}\left(X_{p^{m+1}\left(i\right)}\right)}\left(\frac{V_{p^m\left(i\right)}}{E_{p^m\left(i\right)}^2}\right)+\frac{1}{\mathbb{E}\left(X_{p^M\left(i\right)}\right)}\left(\frac{C_{p^{M-1}\left(i\right),p^{M-1}\left(j\right)}}{E_{p^{M-1}\left(i\right)}{E}_{p^{M-1}\left(j\right)}}\right)}.$$

This equation expresses the covariation in barcode counts between nodes i and j in terms of their normalized covariance (left-hand side). The two terms on the right-hand side describe different sources of covariation. First, fluctuations in the number of cells upstream of i and j’s common ancestor (first term) tend to increase the covariance, since both nodes stand to gain cells when they are plentiful at the common ancestor or lose cells when they are few. Second, the covariance between i and j depends partly on the covariance at the common ancestor itself (second term). All phenomena that occur downstream of the common ancestor have no impact on normalized covariance, which is reflected by the absence of terms that depend on $D_{p^m\left(i\right)}$ and $D_{p^m\left(j\right)}$ where $m<M$. Throughout the following text we denote normalized covariance as

$${\stackrel{\sim }{C}}_{ij}=\frac{\text{Cov}\left(X_i,\hspace{0.17em}{X}_j\right)}{\mathbb{E}\left(X_i\right)\mathbb{E}\left(X_j\right)}.$$

Tree Reconstruction.

From the forward problem—calculating moments from knowledge of the three—we now turn to the reverse problem: reconstructing the tree from knowledge of the moments. A possible starting point is the intuition that closely related lineages should appear more coupled than distant ones. Following this idea, it may be possible to reconstruct the entire topology of the tree by iteratively joining leaves with the highest normalized covariance, similar to the “neighbor-joining” algorithm in phylogentics (27).

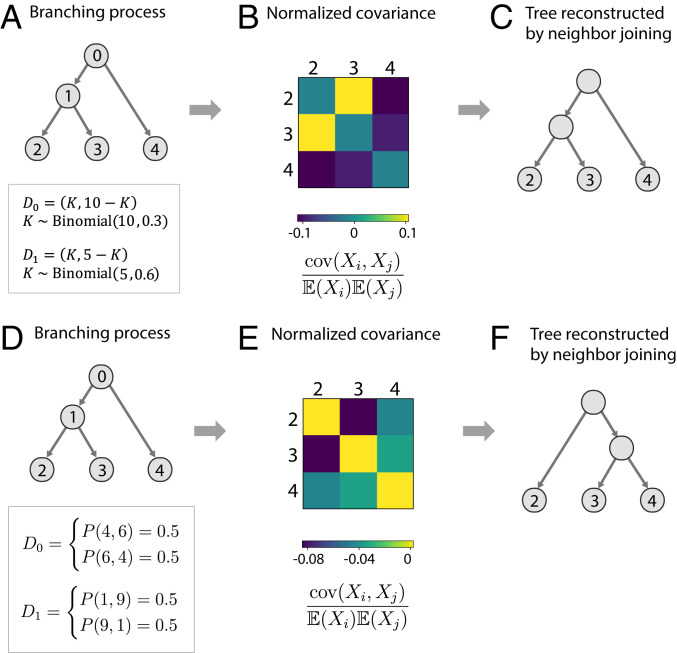
A simple simulation shows that this idea can work in practice (Fig. 2 A–C). It turns out, however, that neighbor joining can fail when sister cells make correlated differentiation choices after division. This would occur when cells in putatively multipotent states are already committed or primed toward a particular downstream lineage. For example, suppose that in the simulated tree (Fig. 2A), cells at node “1” always send their daughters to “2” or “3” but never both simultaneously. This would destroy the correlation of barcode counts between “2” and “3” and indeed would render the topology of the tree meaningless, since node “1” would simply be hosting cells that were already committed to one of the downstream fates. An alternative simulation (Fig. 2 D–F) shows that this pathology can occur even when cells are not fully committed but sufficiently biased toward a particular downstream lineage.

Fig. 2.

Success and failure cases for neighbor joining. (A–C) Successful reconstruction with neighbor joining. (A) Single cells at node 0 expand to 10 that partition binomially between 1 and 4. Each cell arriving at node 1 expands to five that partition binomially between 2 and 3. (B) Normalized covariance of barcode counts reflects the tree structure: the branching at node 1 causes a strong covariance between nodes 2 and 3. (C) Neighbor joining correctly reconstructs the original tree. (D–F) Failure case for neighbor joining. (D) The same tree structure as in A, but with different dynamics of cell division and differentiation. A cell starting at node 0 expands to 10 cells and then sends either four cells to node 1 and six cells to node 4 or six cells to node 1 and four cells to node 4 with equal probability. Each cell arriving at node 1 then sends (1, 9) or (9, 1) cells to nodes 2 and 3 again with equal probability. (B) Although nodes 2 and 3 are closer to each other in the tree than they are to node 4, they nonetheless have a lower normalized covariance with each other than each has with node 4, leading to an incorrect tree (C).

Conditions That Guarantee Validity of Neighbor Joining.

For neighbor joining to correctly construct lineage relationships, we might require that sister cells choose their differentiation fate independently. Formally, an equivalent statement is that the $D_i$ can be parametrized as multinomial distributions with a random number of trials. We prove that this assumption guarantees the correctness of neighbor joining (SI Appendix, Theorem 4). In particular, it implies that for any leaf nodes $\left(i,j,k\right)$, i and j are more closely related in the tree than j and k if and only if ${\stackrel{\sim }{C}}_{ij}>{\stackrel{\sim }{C}}_{ik}$.

Conformal Symmetry.

Neighbor joining will always produce some tree, but how can we know if it is correct? It turns out that the model strongly constrains the normalized covariances in the form of conformal symmetry (17). This symmetry principle means that when nodes i and j are more closely related to each other than they are to a third node k, they must each have the same normalized covariance with k (i.e., ${\stackrel{\sim }{C}}_{ik}={\stackrel{\sim }{C}}_{jk}$; see SI Appendix, Theorem 5). This principle can only be violated if there is noise in the estimates of normalized covariance or if the process being studied does not comply with the model assumptions. There are a number of ways to deviate from the model: barcoding could have happened at multiple stages instead of at a single moment in time, the developmental process could be asynchronous with a mixture of differentiation and self-renewal, or there might be multiple paths to the same end state, meaning development cannot be formally described as a tree. Each of these deviations could affect the results stated so far and highlights opportunities to extend the modeling framework. We will take one of those opportunities here and investigate the effect of multiple paths to the same end state.

Multiple Paths in Development.

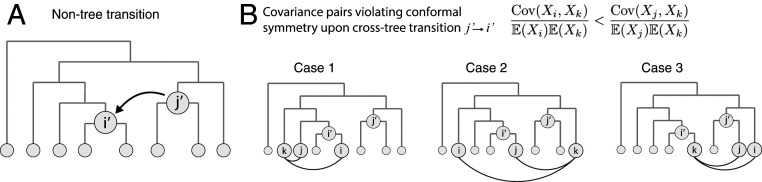
There are several well-documented cases where cells violate a strict tree-like developmental hierarchy (18, 28, 29). We cannot yet provide a general account of how barcode statistics are determined for arbitrary differentiation topologies, but motivated by the observation that cross-tree transitions are usually sparsely superimposed on otherwise tree-like processes we can ask how a single cross-tree transition would affect conformal symmetries on the tree. Suppose that there exists a pair of cell types $i\text{'}$ and $j\text{'}$ that have branched apart, yet a subset of cells differentiates directly from $j\text{'}$ to $i\text{'}$ in violation of the tree structure (Fig. 3A). The resulting normalized covariances would violate conformal symmetry. Can the precise pattern of violations pinpoint the source and target of the cross-tree transition?

Fig. 3.

Conformal symmetry breaking by multiple paths to the same end state. (A) Multiple paths to the same end state can be modeled as a transition across the tree. The figure shows a scenario where cells are transferred from node $j\text{'}$ to node $i\text{'}$. (B) Cross-tree transitions cause specific violations of conformal symmetry. Given a triplet of leaf nodes $i,j,k$ where i and j are more closely related to each other than they are to k, there are three scenarios where symmetry is broken, defined by the positions of $i,j,k$ relative to $i\text{'}$ and $j\text{'}$.

One can show that, for any triplet of nodes $i,j,k$ that would normally satisfy conformal symmetry (with $i,j$ closer to each other than to k), a set of violations can be predicted based on the tree positions of $i,j,k$ with respect to the source and target of the transitioning cells ($j\text{'}$ and $i\text{'}$ respectively; see SI Appendix, Theorem 6 for the precise result and detailed proof). All remaining symmetries are preserved. The set of violated symmetries (Fig. 3B) can be understood as follows. First, if neither i, j, nor k is downstream of $i\text{'}$, then all three nodes will be insulated from the transition and their normalized covariances will continue to satisfy conformal symmetry. Further, if both i and j are both downstream of $i\text{'}$, then their normalized covariances with k will be equally affected by the transition, so again symmetry is maintained. We are left to consider cases where either i or j, but not both, is downstream of $i\text{'}$ (Fig. 3B; cases 1 and 2), or where k is downstream of $i\text{'}$ (case 3). In the former situation, symmetry will be broken if k is closer to $i\text{'}$ than to $j\text{'}$ (case 1), or closer $j\text{'}$ than to $i\text{'}$ (case 2), but not if they are equally close. When k is downstream of $i\text{'}$ (case 3), symmetry will only be broken if $j$ is closer than $i$ to $j\text{'}$, or $i$ is closer than $j$ to $j\text{'}$.

Conformal symmetry violation must occur in all $\left(i,j,k\right)$ triplets falling into cases 1 through 3 above, and only in such triplets. For any particular transition, these triplets typically cover only a minority of the symmetries that would normally exist (e.g., $9\pm 7\%$ for simulated trees with 10 leaf nodes), so each cross-tree transition leaves a specific fingerprint in the form of broken symmetries. Thus, when symmetry breaking is observed in the data, one can compare the observed pattern of broken symmetries to that predicted for each possible cross-tree edge. Close matches could highlight instances where two differentiation paths contribute to the same end state, although alternative causes such as sampling noise or asynchronous barcode integrations should not be ruled out.

Recipe for Data Analysis.

Summarizing the theoretical results, we have shown that neighbor joining based on normalized covariance can accurately reconstruct developmental hierarchies from barcoding data when sister cell fates are independent (Theorem 4), that the normalized covariances should be conformally symmetric with respect to the resulting tree (Theorem 5), and that tree violations in the form of multiple paths to the same end state leave a specific fingerprint in the form of broken symmetries (Theorem 6) that might indicate which alternative paths are present. We now describe a step-by-step approach for applying these results to data. The method is applicable to an experiment where cells are barcoded and allowed to differentiate and the number of cells with each barcode in each differentiated cell type has been measured (see SI Appendix, Supplementary Materials and Methods 1.1 through 1.5 for complete implementation details).

• 1)Calculate the normalized covariance ${\stackrel{\sim }{C}}_{ij}=\frac{\text{Cov}\left(X_i,\hspace{0.17em}{X}_j\right)}{\mathbb{E}\left(X_i\right)\mathbb{E}\left(X_j\right)}$ between each pair of terminal states.
• 2)Pick the pair of states with highest normalized covariance and merge them, forming a new pseudostate whose barcode counts are the sum of the counts from the original pair. Return to step 1, repeating this process until all of the states have been joined together.
• 3)Using the tree obtained from neighbor joining, identify all instances where conformal symmetry is broken with a chosen false-discovery rate (FDR).
• 4)Identify the set of cross-tree transitions that best explains the observed symmetry violations.
• 5)Detect and fix possible distortions in tree topology caused by cross-tree transitions.

We have packaged these steps as a bioinformatic method called CLiNC that is available in Python and R (https://github.com/AllonKleinLab/CLiNC/).

Robustness Tests with Simulated Data.

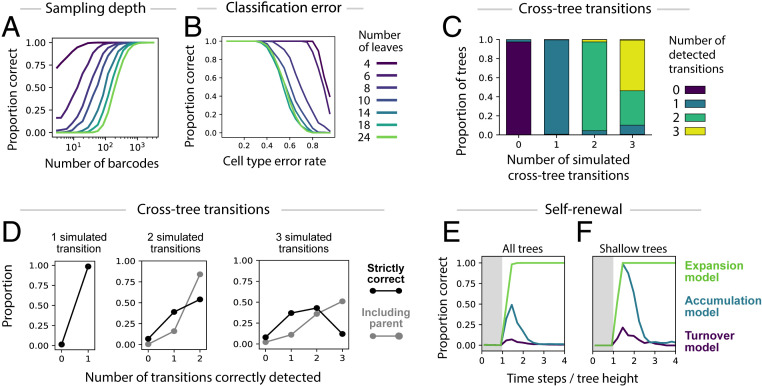
We investigated the robustness of CLiNC using simulated differentiation processes on trees with variable tree size, number of detected clones, error rates in cell type assignment, and number of cross-tree transitions. Considering trees with 4 to 24 leaves (SI Appendix, Fig. S1A), the probability of inferring the correct tree depended on the size of the tree and the number of barcodes, with 1,000 barcoded clones sufficient for all trees tested (Fig. 4A and SI Appendix, Fig. S1 B–D). Simulated error in cell-type assignment had little effect for realistic error rates (<10%) but progressively degraded inference at higher rates in a data-size-dependent manner (Fig. 4B and SI Appendix, Fig. S1 E–G).

Fig. 4.

Robustness tests on simulated data. (A) Inference accuracy (y axis; measured as the fraction of cases where the inferred tree is identical to the ground-truth tree) for increasing numbers of measured barcodes (x axis), for trees of varying size (colored lines). (B) Inference accuracy as a function of error rate in cell-type assignment. (C) Proportion of cases with zero, one, two, or three detected transitions (y axis) in simulations with different numbers of ground truth transitions (x axis). (D) Distribution over number of true positive inferred transitions (x axis), plotted for simulations with different numbers of ground-truth transitions (distinct panels). A strict metric that defines true positives as exact detections of the correct transition is shown in black, and a relaxed metric that defines true positives as detections where the correct nodes or their parents were selected is shown in gray. (E and F) Inference accuracy over time in a system with self-renewal. Time is measured as a fraction of tree height, that is, in proportion to the minimum time required for cells at the root to reach all of the leaves. Three sets of simulations are shown, defined by different behaviors at the leaf nodes, including continual expansion (Expansion model), accumulation without division or death (Accumulation model), and complete replacement at each time step (Turnover model). The gray shaded area indicates the time before barcoded cells have reached all of the leaf nodes. Results for all trees are plotted in E and for shallow trees only (root-to-leaf distance between 3 and 4) in F.

With respect to detecting cross-tree transitions, we found that tree reconstruction was consistently accurate when there was only one cross-tree transition (>95% correct) but decreased as transitions were added (88% for two transitions and 69% for three transitions; SI Appendix, Fig. S1 M and N). In cases where tree inference succeeded, CLiNC accurately detected the number of cross-tree transitions (Fig. 4C), and with only one transition the precise transition was correctly localized in 98.5% of cases. However, accuracy was substantially lower when there were two or three transitions (2/2 correct in 54% of cases and >2/3 correct in 55% of cases; Fig. 4D). Even when inference failed, however, the reported transition was often near the correct one. When including the parents of the correct nodes as acceptable source and target nodes, there was a substantial increase in accuracy (2/2 correct in 84% of cases and >2/3 correct in 87% of cases; Fig. 4D). Together, these results support the accuracy of CLiNC in the case of bona fide trees or those with one transition, which were the cases we considered theoretically (Fig. 3) as the basis for the algorithm. We urge caution when conformal symmetry violations suggest the existence of more than one cross-tree transition.

To further assess robustness, we asked how self-renewal—represented by self-edges and so excluded by our formal model assumptions—would affect the accuracy of tree inference. In simulations, accuracy of tree inference increased during the initial sampling time steps, peaking at a chase period roughly 1.5 times the tree height (tree height = the minimum time for a cell to reach any leaf starting from the root node; Fig. 4E). Thereafter, accuracy was profoundly affected by behavior at downstream leaf nodes: If terminal states were allowed to divide during the experiment (“expansion model”), the fraction of correctly inferred trees was 98% and the peak and remained at or near 100% for all subsequent time points. If these cells instead were continuously replaced (“turnover model”), or they accumulated without dividing or dying (“accumulation model”), then the accuracy of tree construction instead rapidly decreased and subsequently remained close to 0%. In these cases, we found that leaf nodes with similar distance to the root were inappropriately grouped together (SI Appendix, Fig. S1O). Errors caused by self-renewal were mitigated when we restricted to shallow trees where all leaves had similar distance to the root (Fig. 4F). Thus, the accuracy of CLiNC in systems with self-renewal depends critically on the division dynamics of committed cells and on the timing of barcode sampling, and more generally these simulations teach us that correlations observed in clonal data at steady state (11) should be interpreted with caution.

Inferring the Hematopoietic Hierarchy.

We applied CLiNC to analyze published clonal data on hematopoiesis after stem cell transplantation in mice (14). Over several decades, researchers have assembled a detailed map of hematopoietic differentiation and found that it can, on the whole, be described as a tree-like process. Yet several aspects of the tree are the target of ongoing revision (30). Recently, it was shown that both monocyte–neutrophil progenitors and monocyte–dendritic cell (DC) progenitors (31) give rise to monocytes (14, 19), violating a strict tree model. Another question relates to the ontogeny of basophils. Basophils, being a type of granulocyte, are thought to share a progenitor with neutrophilic granulocytes (20, 22, 23). However, recent studies (16, 21, 32) suggest that basophils may in fact be closer to erythrocytes and megakaryoctes. In a previous study (14), we analyzed the trajectory of clones over time to understand how early progenitor state affects fate choice and applied a heuristic permutation-based approach to reconstruct a tree from clonal barcode correlations in terminal states. Here, we revisit the same data to ask whether normalized covariance reconstructs a more accurate hematopoietic tree and if there are violations of conformal symmetry that can identify cross-tree transitions.

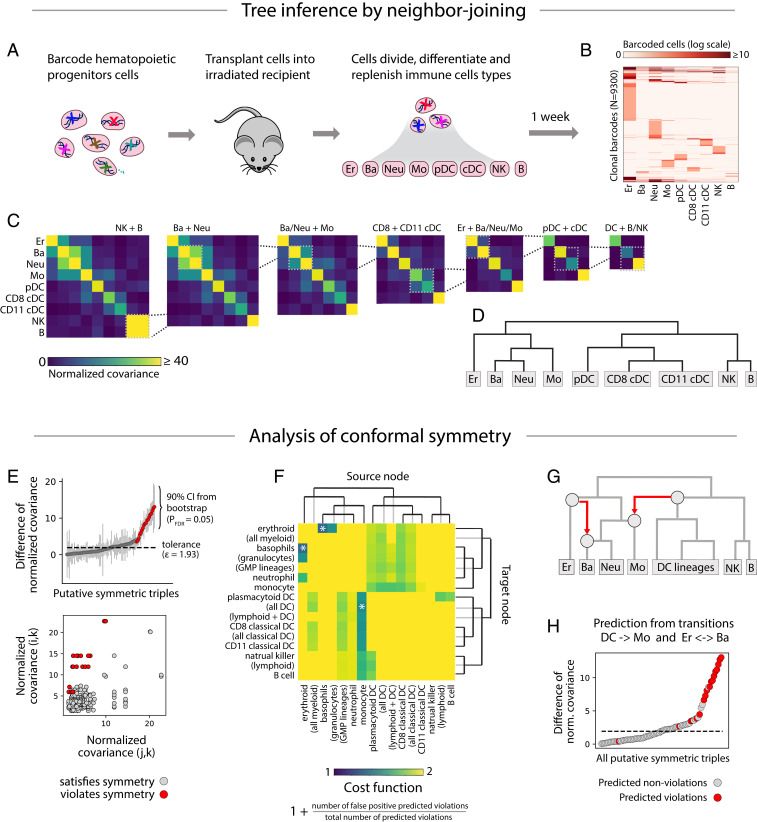
In ref. 14, hematopoietic stem cells and early multipotent progenitor (MPP; Lin⁻ Kit⁺ Sca1^hi) cells were transplanted into sublethally irradiated host mice and then isolated after 1 or 2 weeks of differentiation (Fig. 5A). Using single-cell RNA sequencing, the cell type and barcode sequence of each cell was identified. The resulting data (Fig. 5B) include 93,500 barcoded cells, belonging to 9,300 clones spread across nine cell types, including erythrocytes, basophils, neutrophils, monocytes, three types of dendritic cells, natural killer (NK) cells, and B cells.

Fig. 5.

Analysis of barcoding in hematopoiesis. (A) Hematopoietic progenitor cells were barcoded and transplanted into irradiated recipients where they differentiated into various blood cell types. (B) After 1 to 2 weeks, the transplanted cells were harvested and assigned a cell type identity and barcode sequence using single-cell RNA sequencing. The heat map shows the number of cells with each barcode in each cell type. (C) Lineages with the highest normalized covariance of barcode abundance were progressively merged. The resulting dendrogram (D) represents the lineage relationships predicted by neighbor joining. (E) All putatively symmetric triples $\left(i,j,k\right)$ are plotted as gray dots, positioned by the pair of normalized covariances ${\stackrel{\sim }{C}}_{jk}$ and ${\stackrel{\sim }{C}}_{ik}$ (Bottom), or by their difference (Top). Symmetry violations of the form ${\stackrel{\sim }{C}}_{ik}>{\stackrel{\sim }{C}}_{jk}$ are colored red. (F) For each cross-tree transition, defined by a source node (heat-map columns) and a target node (heat-map rows), the cost function—reflecting the proportion of predicted violations that match the observed violations—is plotted (intensity in heat map). The transitions that minimize cost and cover the predicted violations are marked by an asterisk. They include a transition from the dendritic cell to the monocyte lineage and from the erythrocyte to the basophil lineage. (G) The transitions are shown in red superimposed on the original tree. Together, the transitions explain 13 out of 15 symmetry violations (H; explained violations in red).

As required by our model, cell barcoding was synchronous (likely occurring within 24 h of viral transduction) and applied to a putatively uncommitted starting population. Although hematopoietic cells do self-renew, transcriptional analysis of cell cycle genes showed that 78% of analyzed cells were cycling (SI Appendix, Fig. S2) and prior work suggests the remaining postmitotic cells were likely retained within the bone marrow through the chase period (33, 34). Thus, murine hematopoiesis over 1 to 2 weeks is intermediate between the “expansion” and “accumulation” models investigated in Fig. 4 E and F, and therefore suitable for analysis with CLiNC. Longer-term lineage-tracing experiments (11), however, may perform poorly.

Following the CLiNC pipeline, we computed normalized covariance (Fig. 5C) for each pair of cell types and iteratively joined states with the highest normalized covariance (Fig. 5D), resulting in a hierarchy that agreed with past literature (30). Using an FDR of 2%, we detected 15 symmetry violations (out of 84 putatively symmetric triples; Fig. 5E). Two cross-tree transitions optimally explained these violations (Fig. 5 F–H): An erythroocyte-to-basophil transition explained 2 violations and a transition from the common progenitor of all dendritic cells to the monocyte lineage explained 12 violations.

The detected dendritic-to-monocyte transition is consistent with recent evidence that monocytes may differentiate by two routes: a monocyte–neutrophil pathway and a monocyte–dendritic pathway (19). We previously used barcode data to show that dendritic cell-related monocytes were enriched with dendritic cell gene markers, and likewise for neutrophils (14, 19). Here, we have used the covariance of barcode counts across lineages to provide a complimentary line of evidence for two routes of monocyte differentiation. The detected erythroocyte-to-basophil transition is also intriguing given the ongoing controversy between alternative tree models that place basophils closer to the neutrophil or erythroid lineages (16, 20–23). Our analysis suggests that a strict tree model might not be appropriate for describing the ontogeny of monocytes or basophils.

Together, the dendritic-to-monocyte and erythroid-to-basophil transitions explain 13 out of 15 detected symmetry violations (one violation was predicted by both transitions). The two leftover violations—an increased NK/plasmocytoid-DC (pDC) covariance compared to NK/CD11+ DCs, and an increased monocyte/CD11+ DCs covariance compared to monocyte/CD8+ DCs—could not be parsimoniously explained by cross-tree transitions. The leftover violations might be the result of false discovery (84 putative symmetries with FDR = 2%), or they might represent bona fide alternative differentiation pathways. pDCs may have both lymphoid and myeloid differentiation pathways (35), possibly explaining their increased covariance with NK cells.

Discussion

We defined a model of cell differentiation as a tree-structured branching process, calculated the low-order moments of this process (forward problem), and then showed how to reconstruct the tree from these moments (reverse problem). Analysis of conformal symmetry and the violations induced by cross-tree transitions indicate the broad scope of what can be inferred from barcode statistics alone. Our theoretical results suggest a recipe for the analysis of barcode data that is implemented in Python and R packages available online (https://github.com/AllonKleinLab/CLiNC). The method is well-suited to experimental data from commonly used barcoding methods and immediately applicable to existing datasets, as shown by our reanalysis of a published barcoding study of hematopoiesis.

Yet, these results rely on a set of biological assumptions that do not always apply. The branching process model excludes cell–cell interactions that cannot be expressed in terms of a mean field, such as feedback control of total cell number, and validity of the neighbor-joining algorithm requires that cell division and differentiation can be decoupled. Many processes are well-captured by these assumptions, but certain phenomena, such as strict asymmetric division (36), are not accommodated. The model also ignores cell death or stable propagation of a cell state through self-renewal and assumes that barcodes are all deposited in a single cell type at a single developmental stage, which is only approximately true for many experimental strategies (2, 11, 14) and not true at all for others (8, 9, 15). A more profound deviation from our model is the growing recognition that some fate choices may be better described as continuous processes than as discrete, hierarchical decision trees. Exploring the mathematics of barcode distribution when each of these assumptions is relaxed is an interesting area for further research.

In the meantime, we have tried to provide guidelines that can inform interpretation of CLiNC output and guide the preparation of data (SI Appendix, Fig. S3). Using simulations, we identified the bounds on sampling depth and error rate for minimizing error in tree inference (Fig. 4 A and B), found that inference becomes unreliable when there are more than two cross-tree transitions (Fig. 4 C and D), and showed that the effect of self-renewal is dependent on the division and death kinetics of mature cells (Fig. 4 E and F). Some of these parameters can be estimated without prior knowledge of the system, such as sampling depth and error rate. Others, such as the division kinetics of mature cells, could be inferred from gene expression (SI Appendix, Fig. S2) or measured directly through carefully timed pulse-chase experiments. It remains the case, however, that retrospective analysis from barcoding data should be thought of as a hypothesis-generating tool and that definitive proof of lineage relationships requires prospective labeling or isolation of putative multipotent cell states. As the community establishes future methods for lineage inference, appreciating how various biological processes skew the data will be critical.

Several other biological processes share a statistical structure with barcode fluctuations in differentiation and may also obey the theorems stated here. The core elements are an ensemble of self-replicating units (e.g., barcoded cells) that repeatedly partition within a structured tree (e.g., the lineage hierarchy). Another process with these same elements is the replication and partitioning of plasmids or mitochondria within dividing cells. Here the plasmids and mitochondria represent the replicating units, the precise cell division history represents the structured tree, and horizontal gene transfer represents the cross-tree transitions that might break conformal symmetry. Other examples could include mixed-genotype pathogen transmission between hosts, or the fluctuation of allele counts in a species that spreads in a geographically ramifying pattern. Our approach may be useful for inferring hierarchical structure in these other settings.

Materials and Methods

Robustness Tests on Simulated Data.

Trees were generated using an inhomogeneous branching process. Beginning with a single root node, each node was either assigned to be a leaf (termination of branching) or an internal node with two children (continuation of branching). Differentiation was simulated independently for each “barcode” by initializing a single cell at the root node and then at each stage assigning to each cell a number of children sampled from a Poisson distribution with mean 3, and partitioning the cells binomially to daughters in equal proportions. Self-renewal simulations were carried out on trees with 10 leaves, used 5,000 barcodes, and used a modified differentiation process where the daughters of cells could remain at the same node on the next time step. Simulations with cross-tree transitions were performed on trees with 10 leaves and used 5,000 barcodes. Accuracy for all simulations was evaluated by two metrics: percent correct, which refers to the proportion of cases where the inferred tree was an exact match to the ground-truth tree, and tree distance, in which the predicted and ground-truth tree were compared using the Robinson–Foulds metric.

Analysis of Barcoding Data in Hematopoiesis.

In vivo barcoding data from a recent paper (14) were used (data are available at the Gene Expression Omnibus database under accession no. GSE140802). We removed cell types that were uncommitted progenitors of other cell types also measured in the experiment and excluded rare cell types, defined as those with fewer than 200 shared barcodes (SI Appendix, Fig. S3A). Cells from 1-week posttransplant and 2-week posttransplant were combined for analysis. Tree construction and detection of symmetry violations were carried out using the CLiNC pipeline. Our analysis is fully reproducible (https://github.com/AllonKleinLab/CLiNC/blob/master/clinc_python/example/clinc_pipeline.ipynb).