Optimal quarantine control of an infectious outbreak

Highlights

• •An optimal quarantine control strategy balancing the number of infections and the isolation effort with capacity constraints.
• •A data-driven receding horizon control scheme for newly emerged diseases.
• •Application to COVID-19 data indicates that a sufficiently delayed and controlled lockdown release is optimal.
• •The proposed approaches may support public health authorities in planning quarantine measures.

Abstract

This paper studies the optimal control of an infectious spread based on common epidemic models with permanent immunity and no vaccine availability. Assuming limited isolation control and capacity constraints on the number of infections, an optimal quarantine control strategy that balances between the total number of infections and the overall isolation effort is derived from necessary optimality conditions. The specific optimal policy is then obtained by optimizing the switching times of this generalized strategy. In the case of a newly emerged disease, these results can be used in a data-driven receding horizon manner to improve actions as more data becomes available.

The proposed approach is applied to publicly available data from the outbreak of SARS-CoV-2 in Germany. In particular, for minimizing the total number of infections or the number of isolated individuals, the simulations indicate that a sufficiently delayed and controlled release of the lock-down are optimal for overcoming the outbreak. The approach can support public health authorities to plan quarantine control policies.

1. Introduction

Since the first recorded COVID-19 infections in Wuhan, China, the disease has spread worldwide. There has been a plurality of attempts to interpret and predict the development of the disease based on public data using first-principles epidemiological [1], [2], [3], data-driven [4], or mixed models [5], [6]. Based on these predictions, a wide variety of temporal isolation policies have been established in most affected countries. However, evaluating the effectiveness of these responses is notoriously difficult due to the reliability of available data, and since their impact on the outbreak evolution can only be measured with a substantial delay.

Mathematical analysis of first-principle models of biological systems can provide valuable insight, e.g., on their general properties [25], or how to control infectious disease outbreaks [7]. In the simplest model, the population is divided into the susceptible S, infected I and recovered R groups (therefore called the SIR model), and their evolution over time is represented as a set of coupled ordinary differential equations. Augmenting the state by exposed E individuals, leads to the so-called SEIR model. Applications of outbreak controls minimizing various different cost functions have been proposed for the SIR model, e.g., [8], [9], [10], [11], [12] to name a few, as well as heuristically tailored policies [13], [14]. Although S(E)IR models can be too simplistic for many real outbreaks, they often allow deriving complete analytical solutions, thus providing a foundation for rigorous mathematical results upon which more complex models can be built.

An issue of practical concern for many disease outbreaks without an available vaccine, such as for SARS-CoV-2 as of June 2020, is minimizing the overall quarantine effort or the final outbreak size, while respecting control and capacity constraints on the current number of infections. To account for quarantine measure (similar to [5] and [15]), the SIR model is extended by a quarantined subpopulation Q. Infected individuals are moved depending on the applied control rate from I to Q, where they cannot cause additional infections. Then, using the direct adjoining approach [16] and applying Pontryagin’s Minimum Principle (PMP) to the corresponding state- and input-constrained control problem, in this paper it is shown that bang-bang or bang-boundary controls are admitted in a particular sequence to solve the corresponding optimal control problem. To obtain the specific optimal policy, the switching times between the bang-boundary subarcs are determined in an induced optimization problem. Analogous results can be obtained for the SEIR model. Upon an outbreak of a previously unknown disease, better model parameter estimates can be obtained as more data becomes available, and the induced optimization problem can be recomputed in a data-driven receding horizon manner to improve actions. The proposed methods are applied to publicly available data until June 2020 from the outbreak of SARS-CoV-2 in Germany. In particular, minimizing the total outbreak size or the total number of isolated individuals are studied. The findings of this work can be used to evaluate if the policies that have been established in practice resemble the optimal policy, and support public health authorities in implementing effective future quarantine strategies.

The remainder of this paper is structured as follows. In Section 2, a mathematical statement of the problem is provided. In Section 3, the optimal quarantine policy under isolation control and capacity constraints, and, in Section 4, the data-driven receding horizon control scheme are described. Then, in Section 5, the approach is applied based on COVID-19 data from Germany until June 2020. Finally, the main results and future work are discussed in Section 6.

2. Problem statement

We address epidemics with no vaccine availability, in which the only available control is based on isolation. Let the entire population p be divided into three sub-populations: susceptible S; infected I; and recovered R. Births’ and deaths’ effects are neglected. The recovered population is to be interpreted as those who can no longer infect others, and, who cannot become reinfected by the disease. This is known as the classic epidemiological SIR model [7]. To include quarantine or isolation control, the model is augmented by introducing a time varying quarantine strength control u(t) and a corresponding quarantined (and also recovered from the disease) population Q. Then, with $x={[S,I,R,Q]}^T\subseteq {\mathbb{R}}_{+}^4$ the sub-populations’ evolution is governed by the following system of coupled nonlinear ordinary differential equations:

$$\dot{x}\left(t\right)=f_1(x\left(t\right),u\left(t\right))=\left[\begin{array}{c}-\frac{b}{p}{x}_1\left(t\right)x_2\left(t\right)\\ \frac{b}{p}{x}_1\left(t\right)x_2\left(t\right)-(m+u\left(t\right))x_2\left(t\right)\\ m{x}_2\left(t\right)\\ u\left(t\right)x_2\left(t\right)\end{array}\right],$$ (1)

where the population $p={\sum }_{i=1}^4{x}_i\left(t\right),$ and the infection b and recovery m rates are assumed to be constant in time. Note that the model assumes homogeneous mixing among the sub-populations, as well as uniform susceptibility and disease progress for every individual in the population. The SIR model assumes a direct transition from susceptible to infected. It can be easily augmented by including exposed individuals E to account for a significant incubation period during which individuals have been infected but are not yet infectious themselves. This so-called SEIR epidemiological model [7] has been employed in several prior studies, such as the SARS outbreak, e.g., [17], [18], as well as the COVID-19 outbreak [1], [2], [3]. Since the SEIR model did not provide any additional qualitative insights in the studied problem, for simplicity, the SIR model is analyzed, and details for the SEIR model can be found in the appendix.

An important characteristic of epidemics is the reproduction number

$$R_t=\frac{b}{m+u\left(t\right)}.$$ (2)

Thus, applying the control u(t) results in reducing the effective reproduction number R_t. Determining the maximal quarantine control u _max is highly dependent on local quarantine policies and population specifics, directly corresponding to the minimally achievable reproduction number (2). Another important parameter of epidemics is the fraction α_s of severe conditions among infected individuals requiring hospitalization and admission to an intensive care unit. Highly infectious diseases (with a high R_t) causing many severe conditions in the infected population (corresponding to a high α_s), may quickly lead to an overload of available treatment resources and, thus, cause a large number of additional potentially avoidable deaths. Assuming that the overall available capacity is described by α_c, this capacity limitation can be described as the linear inequality constraint

$$h\left(x\left(t\right)\right)=\alpha x_2\left(t\right)-1,h\left(x\right)\le 0,\alpha =\frac{{\alpha }_s}{{\alpha }_c}.$$ (3)

In this work, the goal is to obtain an optimal quarantine control policy u(t), t ∈ [0, t_f] for a fixed final time t_f, that minimizes a weighted combination of the total number of infections and the overall number of quarantined individuals at time t_f. Note that the overall number of quarantined individuals corresponds to the applied level of containment and can, thus, be linked to the economical impact of the outbreak. The total number of infections is denoted by the sum of the final recovered and final quarantined populations, and is directly correlated to the overall number of deaths. This can be captured by the cost function

$$J(x,u)=g\left(x\left(t_f\right)\right)=w(x_3\left(t_f\right)+x_4\left(t_f\right))+(1-w)x_4\left(t_f\right)=w{x}_3\left(t_f\right)]+x_4\left(t_f\right),$$ (4)

where w ∈ [0, 1]. The control is limited to u(t) ∈ [0, u _max] at all times, such that $u=0$ corresponds to an uncontrolled epidemics evolution, and $u=u_{\text{max}}$ to the case, when maximal possible isolation is applied. Assuming that a solution u(t) ∈ [0, u _max] for t ∈ [0, t_f] exists, this leads to the following (Mayer type) optimal control problem.

Problem 1

For a given initial state x(0) with x ₁(0) > 0, x ₂(0) > 0 and final time t_f, find a function u: [0, t_f] → [0, u _max], such that the cost (4) is minimized subject to the dynamics (1), while respecting the constraint (3) at all times.

In the following, using the direct adjoining approach and applying Pontryagin's Minimum Principle, necessary optimality conditions are derived for the optimal control problem above. Further, it is shown that the obtained locally optimal solutions constitute an optimal generalized strategy under certain assumptions.

3. Optimal quarantine control

As (3) is a pure state constraint, (higher order) time derivatives are used to obtain the control u(t) that yields a system evolution along the active state constraint. Since u(t) appears linearly in the state equation of x ₂ (1), the first total time derivative of the function h(x(t)) (3) contains the control explicitly:

$$h_1\left(x\left(t\right)\right)=\frac{d}{dt}h\left(x\left(t\right)\right)=\alpha \frac{d{x}_2}{dt}=h_{1,a}\left(x\right)+h_{1,b}\left(x\right)u=\alpha x_2(\frac{b}{p}{x}_1-m)-\alpha x_{2}u.$$ (5)

Let an interval [τ ₁, τ ₂] ⊂ [0, t_f] be a boundary arc, if $h\left(x\right(t\left)\right)=0$ for all t ∈ [τ ₁, τ ₂]. If τ ₁ and τ ₂ are maximal, let τ ₁ be the entry-time and τ ₂ the exit-time of the boundary arc. On the boundary arc, h _1,b(x(t)) ≠ 0 must hold ∀t ∈ [τ ₁, τ ₂) (regularity condition). This condition is fulfilled, as α > 0 and $x_2\left(t\right)=\frac{1}{\alpha }>0,$ ∀t ∈ [τ ₁, τ ₂). Thus, the control on a boundary arc is obtained from

$$h_1(x,u_b)=0\iff u_b\left(x\right)=-\frac{h_{1,a}\left(x\right)}{h_{1,b}\left(x\right)}=\frac{b}{p}{x}_1-m.$$ (6)

The boundary control (6) depends on x ₁ and is, therefore, not guaranteed to be in the feasible control set [0, u _max]. Thus, assume that ${\overline{u}}_b\left(x\left(t\right)\right)\in [0,u_{\max }],\forall t\in [{\tau }_1,{\tau }_2]$ (boundedness condition).

To derive first order necessary optimality conditions by applying PMP, a Lagrange multiplier $\eta \left(t\right)\in \mathbb{R}$ associated with the state constraint (3) is introduced. For that, based on the aforementioned regularity and boundedness conditions on a boundary arc, and supposing that the state space constraint is not active at the initial and final time, i.e., h(x(0)) < 0, h(x(t_f)) < 0, the direct adjoining approach [16] is applied. The corresponding augmented Hamiltonian is given by

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {\displaystyle \mathrm{H}(\mathrm{x},\mathrm{u},\lambda ,\eta )}& {\displaystyle =}& {\displaystyle {\lambda }^{\mathrm{T}}{\mathrm{f}}_{\mathrm{n}}(\mathrm{x},\mathrm{u})+\eta \mathrm{h}\left(\mathrm{x}\right)}\hfill \\ & {\displaystyle =}& {\displaystyle (\frac{\mathrm{b}}{\mathrm{p}}{\mathrm{x}}_1-\mathrm{m}){\lambda }_2{\mathrm{x}}_2-\frac{\mathrm{b}}{\mathrm{p}}{\lambda }_1{\mathrm{x}}_1{\mathrm{x}}_2+{\lambda }_3\mathrm{m}{\mathrm{x}}_2}\hfill \\ & & {\displaystyle +\eta (\alpha {\mathrm{x}}_2-1)+({\lambda }_4-{\lambda }_2){\mathrm{x}}_2\mathrm{u},}\hfill \end{array}\end{array}$$ (7)

with the adjoint variable $\lambda \in {\mathbb{R}}^4$. As shown in Maurer et al. [19], there exist an absolutely continuous λ(t) and a piecewise absolutely continuous multiplier function η(t), such that the following optimality conditions hold on [0, t_f]:

$$\dot{\lambda }\left(t\right)=-\frac{dH}{dx},{\lambda }^T\left(t_f\right)=\frac{\partial g\left(x\left(t_f\right)\right)}{\partial x},$$ (8)

$$H(\overline{x},\overline{u},\lambda ,\eta ){|}_{t=tf}=0,$$ (9)

$$H(\overline{x},\overline{u},\lambda ,\eta )=\underset{u\in [0,u_{\text{max}}]}{\min }H(\overline{x}\left(t\right),u,\lambda ,\eta ).$$ (10)

For the SIR model, the following holds:

$$\begin{array}{ccc}\hfill \dot{{\lambda }_1}& =& \frac{b}{p}{x}_2\left(t\right)({\lambda }_1\left(t\right)-{\lambda }_2\left(t\right)),{\lambda }_1\left(t_f\right)=0,\hfill \\ \hfill \dot{{\lambda }_2}& =& -\alpha \eta -\frac{b}{p}{\lambda }_1{x}_1+(\frac{b}{p}{x}_1-(m+u)){\lambda }_2+mw\hfill \\ & & +u,{\lambda }_2\left(t_f\right)=0,\hfill \\ \hfill \dot{{\lambda }_3}& =& 0,{\lambda }_3\left(t_f\right)=w,\to {\lambda }_3\left(t\right)=w,\hfill \\ \hfill \dot{{\lambda }_4}& =& 0,{\lambda }_4\left(t_f\right)=1,\to {\lambda }_4\left(t\right)=1,\hfill \\ \hfill {H|}_{t=tf}& =& 0\iff u\left(t_f\right)=0.\hfill \end{array}$$

As the Hamiltonian (7) is linear in u(t), the optimal control will depend on the sign of the switching function, given by

$$\sigma (x,u)=\frac{\partial H}{\partial u}=(1-{\lambda }_2)x_2.$$ (11)

As suggested in Ledzewicz and Schättler [20], with the total time derivative of (11) and the costates (8),

$$\frac{d\sigma \left(t\right)}{dt}{|}_{u\left(t\right)={\overline{u}}_b}=0$$ (12)

holds on a boundary arc with t ∈ [τ ₁, τ ₂]. This yields the explicit expression for the multiplier

$$\eta \left(t\right)=\{\begin{array}{cc}\frac{1}{\alpha p}(b{x}_1\left(t\right)({\lambda }_1\left(t\right)-1)+mp(1-w)),\hfill & \text{if}h\left(x\right(t\left)\right)=0,\hfill \\ 0,\hfill & \text{if}h\left(x\right(t\left)\right)<0.\hfill \end{array}$$ (13)

Assuming that a solution of Problem 1 exists and the control u(t) has finitely many switching times, the following proposition holds.

Proposition 1

The generalized optimal control policy for Problem 1 is

$$u\left(t\right)=\{\begin{array}{cc}0,\hfill & \text{if}t\in [0,t_1),\sigma \left(t\right)>0,\hfill \\ u_{\text{max}},\hfill & \text{if}t\in [t_1,t_2),\sigma \left(t\right)<0,\hfill \\ u_b,\hfill & \text{if}t\in [t_2,t_3),\sigma \left(t\right)=0\hfill \\ 0,\hfill & \text{if}t\in [t_3,t_f],\sigma \left(t\right)>0,\hfill \end{array}$$ (14)

with 0 ≤ t ₁ ≤ t ₂ ≤ t ₃ ≤ t_f, assuming that u_b(x ₁(t ₂)) ≤ u _max, and

$$\begin{array}{c}{t}_1=t_2,\text{if}{u}_b\left(x_1\left(t_1\right)\right)\le u_{\text{max}},\\ t_1<t_2,\text{if}{u}_b\left(x_1\left(t_1\right)\right)>u_{\text{max}}.\end{array}$$ (15)

If t ₃ > t ₂, the tangency constraints

$$x_2\left(t_2\right)=\frac{1}{\alpha },t_3-t_2=\frac{\alpha p}{b}\text{log}\left(\frac{b}{mp}{x}_1\left(t_2\right)\right)$$ (16)

must also hold.

Proof

On interior arcs, where the state constraint is inactive h(x(t)) < 0, from the minimum condition (10), the optimal control is

$$u\left(t\right)=\{\begin{array}{cc}0,\hfill & \text{if}\sigma \left(t\right)>0,\hfill \\ u_{\text{max}},\hfill & \text{if}\sigma \left(t\right)<0.\hfill \end{array}$$

The switching function (11) is zero $\iff {\lambda }_2\left(t\right)=1$ or $x_2\left(t\right)=0$. The latter case is trivial and will be neglected in the following. To fulfill ${\lambda }_2\left(t_f\right)=0,$ λ ₂(0) > 1 and $\dot{{\lambda }_2}(0+)\le 0,$ such that the optimal control policy may start with a zero segment for [t ₀, t ₁). If u_b(x(t ₁)) > u _max, h(x(t ₁)) < 0, h ₁(x(t ₁)) > 0 and $\sigma (t_1-)<0$ assuming $u(t_1-)=0,$ and as $-\dot{\sigma }\left(t_1\right)(0-u_{\max })>0,$ a second segment for t ∈ [t ₁, t ₂) may have the control u _max.

On a boundary arc, given the regularity and boundedness conditions for the boundary control, the minimum condition (10) yields $\sigma \left(t\right)=0$ and η(t) > 0, t ∈ [τ ₁, τ ₂)⊆[0, t_f]. With $h\left(x\left(t_2\right)\right)=0,$ $h_1\left(x\left(t_2\right)\right)=0,$ u_b(x ₁(t ₂)) ≤ u _max (from the boundedness condition of the boundary control) and ${\dot{x}}_2(t_2+)\left({\overline{u}}_b\right)=0,$ and thus, the continuity conditions on the boundary $\sigma (t_2-)(u(t_2-)-u(t_2+))\ge 0,$ $\dot{\sigma }(t_3+)(u(t_3-)-u(t_3+))>0,$ a boundary arc with (6) may occur, if the Lagrange multiplier η(t) > 0, t ∈ [t ₂, t ₃). Note that if u_b(x ₁(t ₁)) ≤ u _max, a preceding u _max control segment is not necessary. With $\sigma \left(t\right)=0\iff {\lambda }_2\left(t\right)=1,$ $h\left(x\left(t\right)\right)=0\iff x_2\left(t\right)=\frac{1}{\alpha }$ and $u\left(t\right)=u_b,$ the remaining ODE’s are solved as

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {\displaystyle {\dot{x}}_1\left(t\right)}& {\displaystyle =}& {\displaystyle -\frac{b}{p\alpha }{x}_1\left(t\right)\Rightarrow }\hfill \\ \hfill {\displaystyle x_1\left(t\right)}& {\displaystyle =}& {\displaystyle x_1\left(t_2\right)e^{(-\frac{b}{\alpha p}(t-t_2))}}\hfill \\ \hfill {\displaystyle {\dot{x}}_3\left(t\right)}& {\displaystyle =}& {\displaystyle \frac{m}{\alpha }\Rightarrow }\hfill \\ \hfill {\displaystyle x_3\left(t\right)}& {\displaystyle =}& {\displaystyle x_3\left(t_2\right)+\frac{m}{\alpha }(t-t_2)}\hfill \\ \hfill {\displaystyle {\dot{x}}_4\left(t\right)}& {\displaystyle =}& {\displaystyle \frac{b}{p\alpha }{x}_1\left(t\right)-\frac{m}{\alpha }\Rightarrow }\hfill \\ \hfill {\displaystyle x_4\left(t\right)}& {\displaystyle =}& {\displaystyle x_4\left(t_2\right)+x_1\left(t_2\right)(1-e^{(-\frac{b}{\alpha p}(t-t_2))})-\frac{m}{\alpha }(t-t_2)}\hfill \\ \hfill {\displaystyle {\dot{\lambda }}_1\left(t\right)}& {\displaystyle =}& {\displaystyle \frac{b}{p\alpha }({\lambda }_1\left(t\right)-1)\Rightarrow }\hfill \\ \hfill {\displaystyle {\lambda }_1\left(t\right)}& {\displaystyle =}& {\displaystyle ({\lambda }_1\left(t_2\right)+1)e^{\left(\frac{b}{\alpha p}(t-t_2)\right)}-1.}\hfill \end{array}\\ \hfill \end{array}$$

Substituting relevant equations into (13) yields

$$\mu (\tau ,t)=\frac{1}{p\alpha }[b{x}_1\left(\tau \right)({\lambda }_1\left(\tau \right)-2e^{(-\frac{b}{\alpha p}(t-\tau ))}+1)+\mathit{mp}(1-w)].$$

The relation $u_b\left(x\left(t_3\right)\right)=0\iff x_1\left(t_3\right)=mp/b,$ resulting from the boundedness condition of the boundary control, completes the additional tangency constraints (16).

If h(x(t)) < 0 and $\sigma \left(t\right)=0$ for $t\in [{\tilde{\tau }}_1,{\tilde{\tau }}_2),$ a singular arc may occur. Since $\partial \sigma /\partial u=0$ holds trivially, the singular control u_s can be obtained from $d\sigma /dt=0$ with $\eta \left(t\right)=0$ and ${\lambda }_2\left(t\right)=1,$ which yields $u_s=\frac{b}{p}{x}_1-m=u_b$. The optimality of the corresponding singular arc can be checked with the generalized Legendre-Clebsch condition of first order, which yields

$$-\frac{\partial }{\partial u}\left[\frac{d^2}{dt}\frac{\partial H}{\partial u}\right]=-\frac{1}{p}{x}_2\left(t\right)(b{x}_1\left(t\right)({\lambda }_1\left(t\right)-1)+mp(1-w))=-\alpha x_2\left(t\right)\mu ({\tilde{\tau }}_1,t)\ge 0.$$

Transitioning from an interior arc to a singular arc and vice versa at time τ ∈ [0, t_f] violates the continuity conditions $\sigma (\tau -)\left(u\right(\tau -)-u(\tau +\left)\right)\ge 0,$ $\dot{\sigma }(\tau +)(u(\tau -)-u(\tau +))>0$. While transitioning from a boundary to a singular arc and vice versa at time τ ∈ [0, t_f] satisfies the aforementioned continuity conditions, it also has to satisfy

$${\frac{\partial }{\partial u}\left[\frac{d^2}{dt}\frac{\partial H}{\partial u}\right]|}_{t=\tau }=\alpha x_2\left(\tau \right)\mu (\tau ,\tau )\le 0.$$

If the condition above holds for any junction time τ, then μ(t ₂, τ) > 0 for the boundary arc and μ(τ, τ) ≤ 0 for the singular arc would have to hold simultaneously. Thus, a singular arc will not be part of the optimal solution.

Finally, since $h\left(x(t_3-)\right)=0$ and $h_1\left(x(t_3-)\right)=0$ if t ₂ ≠ t ₃, ${\dot{x}}_2\left(t_3\right)(u=0)<0$ and the optimal control (14) ends with a zero segment for t ∈ [t ₃, t_f], which also satisfies the transversality condition (9). □

Remark 1

If u_b(x ₁(t ₂)) ≤ u _max does not hold, by analogous derivations to the proof above, it can be shown that adding a finite number n of sequences of a zero arc followed by an u _max-arc, until a switch to the boundary arc at time $t_{2n+2}$ becomes possible with $u_b\left(x_1\left(t_{2n+2}\right)\right)=u_{\max },$ fulfills the necessary optimality conditions. For simplicity, this case is excluded in the following elaborations.

As a consequence of the above proposition, solutions of Problem 1 will exhibit the structure of the generalized bang-boundary control policy (14). Note that the specific optimal policy strongly depends on the choice of w as well as the model parameters. What remains to be determined are the optimal switching times. Instead of directly optimizing the switching times t ₁, t ₂, t ₃, t ₄, introduce the arc durations ${\xi }_i=t_i-t_{i-1},$ assuming $t_4=t_f$. Thus, the induced optimization problem reads

$$\begin{array}{cc}\underset{{\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4}{\min }& g\left(x\left(t_f\right)\right),\\ \text{s.t.}& \left(1\right),\left(3\right),\left(14\right),\left(15\right),\left(16\right),\sum _{i=1}^4{\xi }_i=t_f,x\left(0\right)=x_0.\end{array}$$ (17)

This optimization problem can be simplified further. If $w=1,$ i.e., the goal is to minimize only the total number of infections, the optimal control is $u\left(t\right)=u_{\max },\forall t\in [0,t_f]$. Similarly, note that the existence of a solution to Problem 1, can be checked, if given an initial state x ₀ and applying $u\left(t\right)=u_{\max },$ there exists no time t ∈ [0, t_f], where the capacity constraint (3) is violated. For other values of w, the optimal control is given by (14), which denotes two possible policies – one containing a boundary arc, and one without a boundary arc. Note that (1) is explicitly solved on the boundary arc, as already used in the proof of Proposition 1. Thus, solving (17) can be replaced by solving the three aforementioned boundary value problems and choosing the policy that yields the minimal cost.

Corresponding derivations for the SEIR model can be found in the appendix. The induced optimization problem (17) can be recomputed in a data-driven manner to obtain an improved quarantine action, as shown in the following.

4. Data-driven receding horizon control

While a fast response upon an epidemic outbreak is essential, for a newly emerged disease, like in the case of COVID-19 at the beginning of 2020, disease characteristics are highly uncertain. As more data and insights become available over time, it can be expected that the parameter estimates of the models can be improved continuously. This can be achieved, e.g., by minimizing the mean square error loss function between measured state data $\tilde{x}$ until time τ and the state trajectory predicted by the model with respect to the parameters $\mathcal{P}=\{b,m\}$ of the SIR model, i.e.,

$$\begin{array}{cc}\underset{\mathcal{P}}{\min }& \sum _{t=0}^{\tau }\sum _{i=1}^{n_j}{\parallel x_i\left(t\right)-{\tilde{x}}_i\left(t\right)\parallel }^2,\\ \text{s.t.}& \left(1\right).\end{array}$$ (18)

Analogously, this can be done for the SEIR model with $\mathcal{P}=\{b,m,c\}$.

At any time τ, using the parameter estimates ${\mathcal{P}}_{\tau }$ obtained by (18) and the measured state $\tilde{x}\left(\tau \right),$ the induced optimization problem (17) can be re-solved with $x_0=\tilde{x}\left(\tau \right)$. Assume that the parameter estimates are updated whenever new data becomes available. Based on that, a data-driven receding horizon approach is adopted, where the control is obtained by re-computing (17), only when the current parameter estimates deviate from the parameter estimates used in the previous computation step evaluated by a function ζ by a pre-defined threshold δ. The similarity function ζ was assumed to be a simple absolute deviation in this work, but it can contain more complex considerations like, e.g., the covariance of the estimates. This leads to Algorithm 1.

Algorithm 1.

Data-driven receding horizon control at time τ.

Note that, in general, receding horizon control approaches with uncertain parameters cannot guarantee that hard constraints will not be violated. Thus, to increase satisfaction probability, the capacity constraint (3) can be tightened conservatively based on the confidence of the current parameter estimate ${\mathcal{P}}_t$.

5. Application to SARS-CoV-2 outbreak data from Germany

The proposed method is applied to data from the SARS-CoV-2 outbreak in Germany until June 2020. Two cases are considered – $w=0$ and $w=0.5,$ which correspond to minimizing only the overall number of isolated individuals and a trade-off between the overall number of isolated individuals and the total size of the outbreak, respectively. The optimization problems are solved with SciPy’s bvp and minimize routines.

5.1. Parameters

Most parameters are taken from a report of the German Robert Koch Institute [21] – a susceptible population of $x_1\left(0\right)=80.{10}^6$ and an initial number of infections $x_2\left(0\right)=1000,$ corresponding to the number of registered infections in Germany on March 8, 2020. The initial numbers of recovered and quarantined individuals are both 0. For the SEIR model, an initial exposed individuals number of 100 is assumed. Further, a basic reproduction number $R_t=2.0$ is assumed in the uncontrolled models, as well as an inverse mean infectious period in days of $m=0.091$. The percentage of infected individuals admitted to an intensive care unit is 1.2% and the mortality is 0.5%. The overall number of intensive care units in Germany was ${\alpha }_c=40.{10}^3$ by the end of March 2020 [22]. The assumed maximum control value u _max is defined such that it leads to an effective reproduction number ${\tilde{R}}_t=1.0,$ i.e., with Eq. (2) given by $u_{\max }=0.091$.

For the receding horizon control approach, publicly available data from RKI from March 1 until June 1, 2020 to re-estimate the parameters ${\mathcal{P}}_1=\{b,c,m\}$ for this time period, and assume the actual parameters $R_t=2.5,$ $c=0.25$ and $u_{\max }=0.068$ thereafter. The control is re-computed according to Algorithm 1.

5.2. Analysis

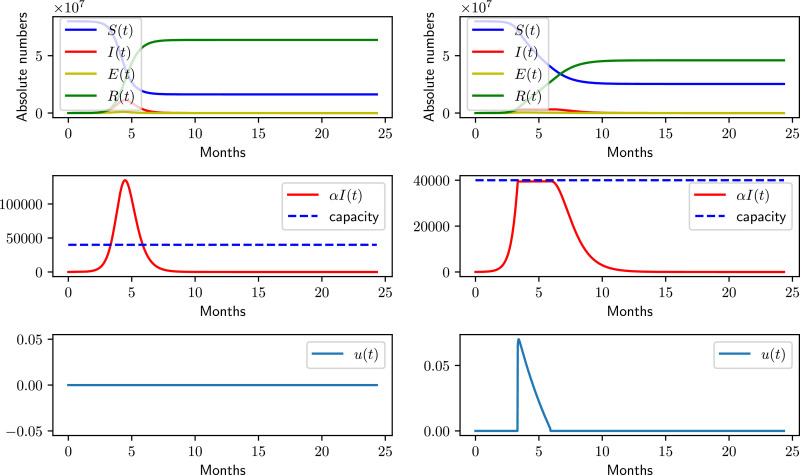
Figs. 1 and 2 show the model state trajectories, the capacity constraint and the control over time for the uncontrolled (left) and the optimally controlled (right) with the aforementioned parameters for the SIR and SEIR model, respectively. It is notable that for both cases, i.e., for $w=0$ and $w=0.5,$ respectively, the optimal solution is given by a bang-boundary control, when using the SIR or the SEIR model.

Fig. 1.

Solutions using the SIR model. The left column shows the uncontrolled case, and the right column – the optimal solution for both $w=0$ and $w=0.5$.

Fig. 2.

Solutions using the SEIR model. The left column shows the uncontrolled case, and the right column – the optimal solution for both $w=0$ and $w=0.5$.

Applying the optimal control to the SIR model under the given assumptions, the pandemic is predicted to lead to an expected total number of cases of 54 084 981, and a total number of deaths of 270 424. The simulations also indicate that the turnaround (final peak of active cases) should occur 26 weeks after the start of the outbreak. The overall outbreak should be completely overcome after 44 weeks, without a second wave of infections. This closely resembles predictions made in an der Heiden and Buchholz [21] and [23].

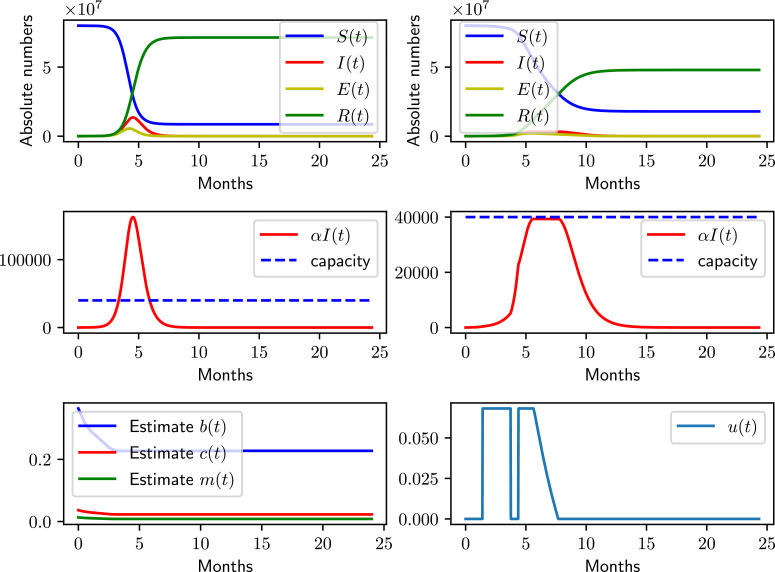
Fig. 3 shows the result with the data-driven receding horizon control. Due to the high estimate of the reproductive number in the initial phase, the maximal isolation control starts earlier, and, overall, applies more isolation due to the parameter uncertainty. Note that the control maintains the capacity constraint. In practice, a toggling between bang-bang controls could be prevented by introducing a hysteresis, when a new control policy is computed in Algorithm 1.

Fig. 3.

Data-driven receding horizon quarantine control of the SEIR model. The left column shows the uncontrolled dynamics, and the estimate of the parameters. The right columns depict the controlled result with Algorithm 1.

Applying the optimal control under the given assumptions, the pandemic is predicted to lead to an expected total number of cases of 49 004 201, and a total number of deaths of 245 021. Note that the lower number of infections is a consequence of the longer period of applied quarantine control compared to the preceding simulation example. Another consequence of the longer quarantine is a slightly delayed turnaround that should occur 30 weeks after the start of the outbreak. The overall outbreak should be completely overcome after 50 weeks, without a second wave of infections, and while control and capacity constraints are maintained at all times.

6. Summary and discussion

The optimal quarantine control of an infectious spread was studied assuming an SIR epidemic model with permanent immunity and no vaccine availability. The control strategy, which minimizes the final outbreak state assuming that only limited quarantine control is available and capacity constraints have to be respected, was derived from necessary optimality conditions. The solution is to possibly delay the control action first, and then, if needed, apply maximal isolation. If the capacity boundary is reached, a boundary control maintaining the infection numbers may be applied afterwards, until the infection numbers begin to drop. This result was used in a data-driven receding horizon control approach to improve actions as more data becomes available for a previously unknown disease. The application of the proposed schemes to publicly available data from the outbreak of SARS-CoV-2 in Germany indicate that a sufficiently delayed and controlled release of the lockdown are optimal, and would result in overcoming the outbreak within one year.

Note that a constant overall population was assumed throughout this work. Effects resulting from population exchange could be addressed, e.g., as suggested in Xue et al. [24], leading to a stochastic induced optimization problem. An interesting remaining question is how to determine the maximal isolation control value, as well as how to map the boundary control values to practical isolation actions. A promising approach for addressing both topics could be using machine learning techniques, e.g., building upon ideas from [5]. Another research direction could be to embed the parameter estimation uncertainty into the data-driven optimization to achieve an improved exploration-exploitation trade-off.

CRediT authorship contribution statement

Vladislav Nenchev: Conceptualization, Methodology, Software, Writing - original draft.

Declaration of Competing Interest

The author declares that he has no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Optimal control for the SEIR model

Including quarantine control analogously to (1), the sub-populationsâ evolution in the SEIR model is governed by the following system of coupled nonlinear ordinary differential equations:

$$\dot{x}\left(t\right)=f_1(x\left(t\right),u\left(t\right))=\left[\begin{array}{c}-\frac{b}{p}{x}_1\left(t\right)x_2\left(t\right)\\ c{x}_3\left(t\right)-(m+u\left(t\right))x_2\left(t\right)\\ \frac{b}{p}{x}_1\left(t\right)x_2\left(t\right)-c{x}_3\left(t\right)\\ m{x}_2\left(t\right)\\ u\left(t\right)x_2\left(t\right)\end{array}\right],$$ (19)

where $x={[S,I,E,R,Q]}^T\subseteq {\mathbb{R}}_{+}^5,$ the population $p={\sum }_{i=1}^5{x}_i\left(t\right),$ and b and c denote the exposure and infection rates, respectively. The reproduction number remains as defined in (2). Analogously to the elaborations provided for the SIR model, the most important equations are derived as:

$$\begin{array}{ccc}\hfill {\displaystyle h_1\left(x\right)}& =& {\displaystyle \alpha x_2\left(t\right)(c{x}_3\left(t\right)-(m+u\left(t\right)))}\hfill \\ \hfill {\displaystyle u_b\left(x\right)}& =& {\displaystyle c\frac{x3\left(t\right)}{x2\left(t\right)}-m}\hfill \\ \hfill {\displaystyle H(x,u,\lambda ,\eta )}& =& {\displaystyle -\frac{b}{p}{\lambda }_1{x}_1{x}_2+{\lambda }_{4}m{x}_2+{\lambda }_5{x}_{2}u+(\alpha x_2-1)\eta }\hfill \\ & & {\displaystyle +(c{x}_3-(m+u)x_2){\lambda }_2+(\frac{b}{p}{\lambda }_1{x}_1{x}_2-c{x}_3){\lambda }_3}\hfill \\ \hfill {\displaystyle \dot{{\lambda }_1}}& =& {\displaystyle \frac{b}{p}{x}_2\left(t\right)({\lambda }_1\left(t\right)-{\lambda }_3\left(t\right)),{\lambda }_1\left(t_f\right)=0,}\hfill \\ \hfill {\displaystyle \dot{{\lambda }_2}}& =& {\displaystyle -\alpha \eta +\frac{b}{p}{x}_1({\lambda }_1-{\lambda }_3)+(m+u){\lambda }_2-m,{\lambda }_2\left(t_f\right)=0,}\hfill \\ \hfill {\displaystyle \dot{{\lambda }_3}}& =& {\displaystyle c({\lambda }_3-{\lambda }_2),{\lambda }_3\left(t_f\right)=0,}\hfill \\ \hfill {\displaystyle \dot{{\lambda }_4}}& =& {\displaystyle 0,{\lambda }_4\left(t_f\right)=w,\to {\lambda }_3\left(t\right)=w,}\hfill \\ \hfill {\displaystyle \dot{{\lambda }_5}}& =& {\displaystyle 0,{\lambda }_5\left(t_f\right)=1,\to {\lambda }_5\left(t\right)=1,}\hfill \\ \hfill {\displaystyle \sigma \left(t\right)}& =& {\displaystyle w_u-{\lambda }_2\left(t\right)x_2\left(t\right)}\hfill \\ \hfill {\displaystyle \eta \left(t\right)}& =& {\displaystyle \frac{b}{\alpha p}({\lambda }_1\left(t\right)-{\lambda }_3\left(t\right))x_1\left(t\right)+\frac{c}{\alpha x_2\left(t\right)}{\lambda }_2\left(t\right)x_3\left(t\right)-\frac{m}{\alpha }}\hfill \end{array}$$

Following an analogous approach, Proposition 1 can be proven for the SEIR model, yielding an identically structured optimal policy.