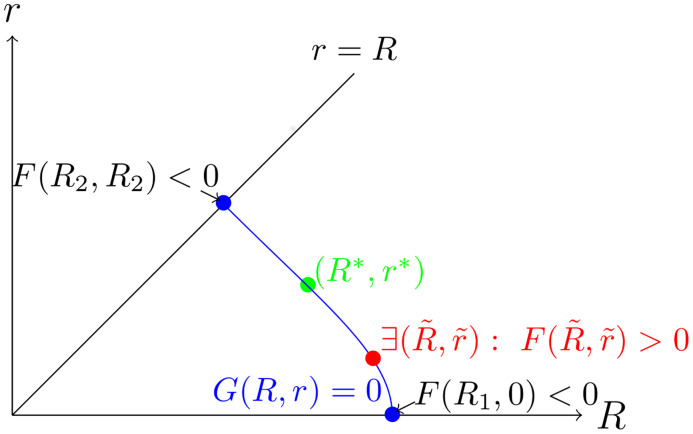
Fig 5. Existence of steady state.

The blue curve describes the zero level-set of function G. The points (R₁, 0) and (R₂, R₂) correspond to the intersection of the zero level-set of function G with the lines r = 0 and r = R. The value of the function F in these points is negative. For r = 0 and r = R we are able to solve (1) explicitly. Moreover, we know that there exists at least one point $(\tilde{R},\tilde{r})$ for which function F is positive. The latter is a consequence of the parameter choice. Thus there exists at least one point (R*, r*) such that: G(R*, r*) = 0, F(R*, r*) = 0 and in the neighborhood of this point for R > R* it holds F(R, r*) ≥ 0 and for R < R* it holds F(R, r*) < 0. Further on, we will consider the stability of the steady state solution (R*, r*).