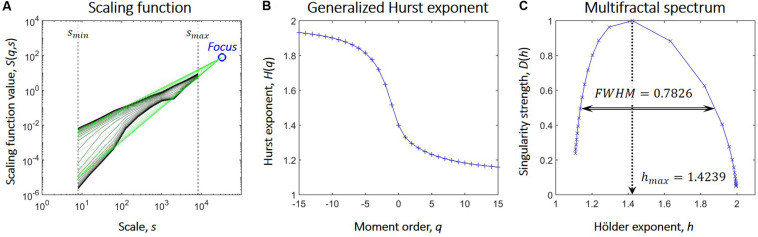
FIGURE 1.

Steps of focus-based multifractal analysis. (A) After the scaling function (marked in black) is acquired, linear regression is used to fit power-law functions (marked in green) at each moment order q. On double logarithmic plots these appear as linear functions whose slopes are the scaling exponents. Also, in case of finite length signals, these converge to one point, the Focus, that is used as a reference point during regression. (B) The generalized Hurst exponent, H(q) is acquired as the scaling exponents of the functions fitted on the scaling function at each value of q. The focus-based formalism enforces the monotonously decreasing nature of H(q); a prerequisite for Legendre transformation. (C) The multifractal spectrum is acquired from H(q) via Legendre transformation and is described by the Hölder exponent at its maximal value (h_max) and its full width at half maximum (FWHM).