Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2020 Jul 31;10:12983. doi: 10.1038/s41598-020-69909-9

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2020

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

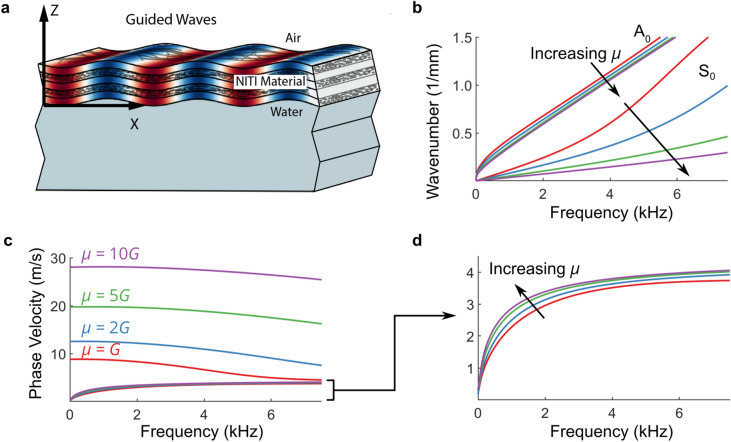
PMC Copyright notice

Analytical solutions for guided wave behavior in a bounded NITI layer. (a) Propagation of harmonic guided waves in cornea tissue, modeled as a NITI material layer bounded above by air and below by water. Dispersion relations for propagating guided modes are derived from partial wave solutions to the elastic wave equations satisfying corneal boundary conditions in Supplementary Note 4. (b) The effect of increasing anisotropy on fundamental (zero order) A₀ and S₀ modes (G = 20 kPa, h = 0.55 mm, varying μ) presented in wavenumber-frequency space. The behavior of the A₀ mode is primarily governed by G, and the S₀ mode by μ. (c) The same dispersion curves in phase velocity versus frequency representation. (d) Zoomed view of the A₀ mode in phase velocity versus frequency representation—the high-frequency asymptote of the A₀ mode depends primarily on G, with its low-frequency rate of change governed by μ.