Figure 3.

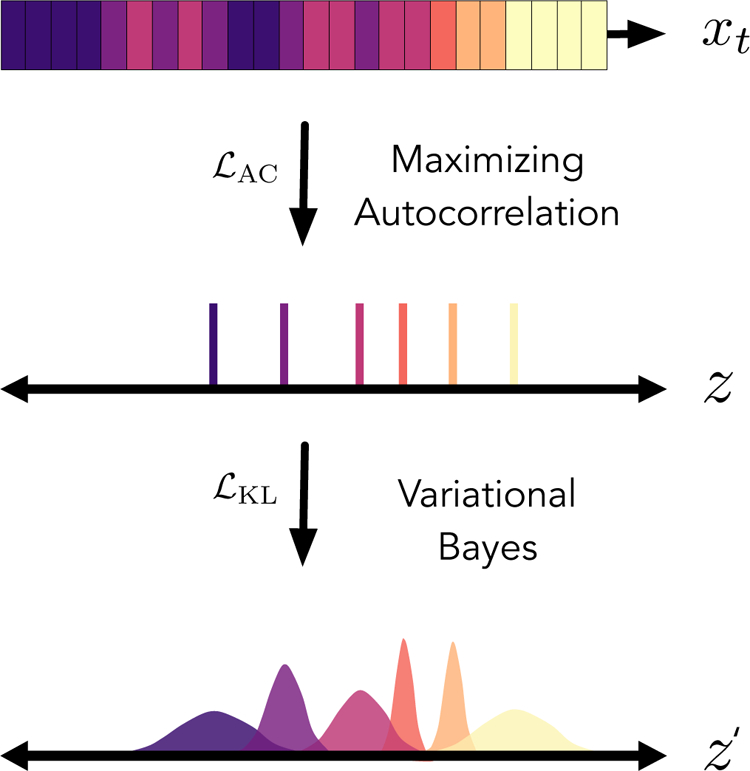
A diagram representing the effects of the autocorrelation loss and KL-divergence loss functions on the VDE latent space. A trajectory, x, which contains several states represented by different colors, can be mapped onto a latent space, z. Here, we randomly select frames from x from each state to be mapped onto z. Maximization of the autocorrelation of z ensures that the slowest process within a trajectory can be modeled continuously within the latent space. Perturbation of the latent space with learnable, value-specific Gaussian noise enables a variational Bayes approach for propagating values from the original trajectory, x. In doing so, we are also able to infer the posterior probability of values within z and effectively perform sampling within the latent space.