Mapping hepatocyte size in vivo using temporal diffusion spectroscopy MRI

Abstract

Purpose

The goal of this study is to implement a noninvasive method for in vivo mapping of hepatocyte size. This method will have a broad range of clinical and preclinical applications, as pathological changes in hepatocyte sizes are relevant for the accurate diagnosis and assessments of treatment response of liver diseases.

Methods

Building on the concepts of temporal diffusion spectroscopy in MRI, a clinically feasible imaging protocol named IMPULSED (Imaging Microstructural Parameters Using Limited Spectrally Edited Diffusion) has been developed, which is able to report measurements of cell sizes noninvasively. This protocol acquires a selected set of diffusion imaging data and fits them to a model of water compartments in tissues to derive robust estimates of the cellular structures that restrict free diffusion. Here, we adapt and further develop this approach to measure hepatocyte sizes in vivo. We validated IMPULSED in livers of mice and rats and implemented it to image healthy human subjects using a clinical 3T MRI scanner.

Results

The IMPULSED‐derived mean hepatocyte sizes for rats and mice are about 15‐20 µm and agree well with histological findings. Maps of mean hepatocyte size for humans can be achieved in less than 15 minutes, a clinically feasible scan time.

Conclusion

Our results suggest that this method has potential to overcome major limitations of liver biopsy and provide noninvasive mapping of hepatocyte sizes in clinical applications.

1. INTRODUCTION

Hepatocytes constitute approximately 80% of the mass of the liver, are the main functional cells in the liver, and perform a remarkable number of metabolic, endocrine, and secretory functions. Gross architectural and morphological changes of hepatocytes are associated with essential biological events, including cell shrinkage during apoptosis ¹ , ² , ³ and cell swelling during hepatocyte polyploidization. ⁴ , ⁵ Abnormal morphological assessments of hepatocytes may have significant clinical implications. For example, hepatocellular ballooning associated with cell swelling is a key finding in nonalcoholic steatohepatitis. ⁶ Small cell changes, defined as hepatocytes showing decreased cell volume, and doubling of cell crowding (increased cell density compared with surroundings) are specific pathological features of early hepatocellular carcinoma. ⁷ Currently, such information can be obtained only by liver biopsy, an invasive and imperfect gold standard. ⁸ , ⁹ Noninvasive in vivo characterization of liver microstructure, notably, hepatocyte size, would have significant value in the diagnosis and clinical management of liver diseases, and reduce the use of liver biopsy.

Recently, a novel diffusion MRI–based framework, temporal diffusion spectroscopy (TDS), has been developed, which provides quantitative information on tissue microstructure such as cell size and density. ¹⁰ , ¹¹ Different from conventional diffusion MRI methods, the TDS approach uses diffusion gradients with different temporal waveforms, such as oscillating gradients at different frequencies, to sample diffusion spectra. Quantitative measurements of tissue microstructure are then obtained by analysis of the frequency (equivalent to the time) dependence of the diffusion coefficients of tissue water, which can be interpreted using specific models of restrictions and hindrances to free diffusion. Although TDS is a generalized framework for the design of diffusion experiments with appropriate frequencies for better sensitivity to selected length scales, the hardware limitations on typical MRI scanners usually constrain the frequencies achievable. We have previously found that acquisitions using two different diffusion gradient waveforms (ie, conventional pulsed gradients and cosinusoidal gradients) can cover a broad range of diffusion frequencies, which correspond to diffusion times that provide high sensitivity to 5‐25 μm, covering typical cell sizes in biological tissues. Because this approach uses a practically limited narrow spectral range, we term this specific implementation of TDS Imaging Microstructural Parameters Using Limited Spectrally Edited Diffusion (IMPULSED). We have previously validated that IMPULSED can accurately quantify mean cell sizes in vitro for different cancer cell types, independent of cell densities, ¹² , ¹³ and can noninvasively map changes of intracellular structure and cell sizes in solid tumors with the spatial resolution of MRI, in cell cultures and in animal models, early during specific treatments. ¹⁴ , ¹⁵ , ¹⁶ We have also successfully implemented IMPULSED on a clinical 3T MRI scanner ¹⁷ for patient studies.

The IMPULSED protocol quantifies the dependence of diffusion coefficients on the diffusion time (t_diff), which may vary, typically, from 5‐70 ms, corresponding to length scales of approximately 6‐20 µm at body temperature. Most of the mass of liver consists of tightly packed hepatocytes with size ranging from 15‐25 µm. ¹⁸ , ¹⁹ , ²⁰ Water diffusion in hepatocytes is therefore restricted, leading to an increased ADC as t_diff decreases. A dependence of the ADC on t_diff has previously been reported in rat and human livers using stimulated‐echo DWI. The ADCs of human livers increased from 0.9 to 1.1 µm²/ms with t_diff decreasing from 186‐33 ms, ²¹ and those of rat livers increased from 0.7 to 0.9 µm²/ms with t_diff decreasing from 200‐15 ms. ²² However, these studies did not include measurements of ADC at sufficiently short diffusion times when intracellular water appears to be relatively unrestricted. To the best of our knowledge, this study is the first study to measure ADCs of livers at very short diffusion times (eg, 2.5 ms, 5 ms), and we found that ADC values continue to increase as t_diff decreases (eg, from 10 ms to 2.5 ms), ultimately tending toward the value of free water. It is therefore necessary to probe a broad range of diffusion times to fully characterize the tissue structures that affect ADC. Fortuitously, the range needed to assess common cell types is readily achievable using appropriate pulse sequences that can sample diffusion times in the range of approximately 1 to 100 ms, corresponding to free diffusion displacements of approximately 2 to 25 µm. We previously described a specific protocol named IMPULSED, ¹³ , ¹⁷ in which a selected set of diffusion data is acquired and fit to a model of water compartments in tissues to derive robust estimates of cell sizes that restrict diffusion. Here, we adapt this approach to measure hepatocyte sizes in vivo. In the preclinical validation studies, IMPULSED‐derived hepatocyte sizes in healthy mice and rats were compared with histological findings. In the human application studies, we developed a protocol with a scan time of less than 15 minutes on a clinical 3T MRI scanner and evaluated the data precision in healthy human subjects.

2. THEORY

A combination of pulsed gradient spin echo (PGSE) and oscillating gradient spin echo (OGSE) diffusion MRI acquisitions are used to assess diffusion properties of livers from relatively long (about 40 ms and 70 ms for animal and human studies, respectively) to very short (about 2.5 ms and 5 ms for animal and human studies, respectively) diffusion times. The normalized, fat‐saturated, MR signals of liver tissues acquired at different combinations of b‐values and effective diffusion times (t_diff) are expressed as the sum of restricted diffusion in liver cells, hindered diffusion in the extracellular extravascular spaces, and dephasing of signals from blood, or intravoxel incoherent motion (IVIM) effects, namely,

$$S_{\mathit{liver}}\left(b,t_{\mathit{diff}}\right)=\left(1-{\mathrm{f}}_{\mathit{IVIM}}\right)S_{\mathit{tissue}}\left(b,t_{\mathit{diff}}\right)+{\mathrm{f}}_{\mathit{IVIM}}{S}_{\mathit{blood}}\left(b,t_{\mathit{diff}}\right)$$

$$S_{\mathit{tissue}}\left(b,t_{\mathit{diff}}\right)=v_{\mathit{in}}{S}_{\mathit{in}}\left(b,t_{\mathit{diff}}\right)+\left(1-v_{\mathit{in}}\right)S_{\mathit{ex}}\left(b,t_{\mathit{diff}}\right),$$ (1)

where f_IVIM is the blood volume fraction from perfusion; v_in is the water volume fraction of intracellular extravascular space; and S_in, S_ex, and S_blood are the MRI signal magnitudes per volume from the intracellular, extracellular, extravascular, and intravascular spaces, respectively. This analysis assumes that the effects of water exchange between the intracellular and extracellular spaces, as well as between blood and tissues, are negligible during the diffusion time chosen. This approximation is also suggested in previous models of diffusion in tumors, ¹² , ²³ and is especially justifiable for short diffusion times. ²⁴

2.1. Modeling intracellular diffusion (S_in)

Theoretically, the diffusion coefficient of intracellular water is affected by contributions that restrict free movements from all organelles and cytoplasmic contents. The biggest organelle inside hepatocytes is the nucleus (6‐8 µm in diameter). About 7%‐10% surface area of a nucleus is occupied by nuclear pore complexes, ²⁵ , ²⁶ which allow small proteins and molecules with molecule weight less than 40 kDa (note that the molecular weight of water is about 18 Da) to translocate between cytoplasm and cell nucleus by passive diffusion. ²⁷ , ²⁸ Therefore, the nuclear membrane has been considered to permit nearly free passage of water molecules between the nucleus and cytosol. ²⁸ , ²⁹ , ³⁰ , ³¹ The sensitivity of MR diffusion measurements at different diffusion times to variations in intracellular structure, in particular, to effects of nuclear size, has previously been investigated numerically by simulating diffusion in a 3D, multicompartment tissue model. ³² The ADC values obtained at b‐value = 1 µm²/ms and at diffusion times ranging from 1‐40 ms showed no apparent changes when the ratio of nuclear volume to cell volume increased from 0% to 30%, covering the range of nuclear‐to‐cell‐volume ratios reported previously and found in our histology analysis.

Moreover, other than the largest organelle nuclei, there are many other intracellular organelles such as Golgi, cytoskeleton, and microtubules. We have previously investigated the influences of these organelles ³³ and found out that these organelles affect ADC measurements slightly (about 4%) at very short diffusion times (OGSE frequency > 1600 Hz). Because only frequencies between 50 Hz and 100 Hz are used in the current human and animal studies, respectively, it is reasonable to assume that these intracellular organelles have negligible influences on the estimation of cell size.

Therefore, restrictions by hepatocyte membranes dominate the diffusion effects on S_in. The diffusion within hepatocytes is modeled as restricted diffusion within hollow spheres of diameter d. The analytical expressions of intracellular diffusion (S_in) for MRI pulse sequences using different gradient waveforms (eg, truncated oscillating and bipolar) have been reported previously ¹⁰ , ¹⁷ as a function of dimension d and the intrinsic intracellular diffusion coefficient D _in.

2.2. Modeling extracellular diffusion

Previous studies have suggested that the extracellular diffusion coefficient shows an approximately linear dependence on the gradient frequency, proportional to the inverse of diffusion time. ³⁴ In our previous preclinical studies (using oscillating frequency up to 150 Hz with SNR = 50), ¹³ the extracellular diffusion was modeled as $D_{ex0}+\beta ·f$, where β represents the linear dependence of extracellular diffusion coefficient on the oscillating gradient frequency. The fitted β maps had large variations (relative SD [RSD] ~ 60%), whereas the fitted mean cell size maps had very small variations (RSD ~ 8%). This variation within parametric maps is a combination of tissue inhomogeneities and fitting uncertainties due to multiple factors (eg, SNR levels, fitting algorithms, and lower sensitivity to the fitted parameters). The dramatic difference between variations of β and cell size maps from the same tissue suggests that diffusion measurements with oscillating frequencies up to 150 Hz do not provide enough sensitivity for reliable fitting of the dependence of extracellular diffusion coefficients on the diffusion time. The frequency range used in this study is narrower, so the variation of extracellular diffusion with frequency is minor. Therefore, we modeled the extracellular diffusion coefficient as a constant D_ex, and S_ex is expressed as

$${\mathrm{S}}_{\mathit{ex}}\left(b,t_{\mathit{diff}}\right)=\exp \left(-b\ast D_{\mathit{ex}}\right).$$ (2)

2.3. Removing the effect of blood microcirculation

The potential influence of blood on diffusion measurements has usually been ignored in similar previous analyses. However, because of the relatively high perfusion and tissue volume fraction of blood in liver, ³⁵ , ³⁶ the influences of signal dephasing in the vasculature cannot be ignored here. To complicate matters, the influence of blood perfusion has been found to be dependent on the diffusion gradient waveforms and diffusion times used. ³⁷ This makes IMPULSED more susceptible to blood microcirculation effects, because multiple diffusion times and waveforms are used. To remove such effects, we implement an approach that is similar to a previous report by Taouli and Koh. ³⁶ Specifically, for each diffusion time, we first extrapolated the signal curves acquired over the range 0.2 ms/µm² ≤ b ≤ 1.0 ms/µm² to obtain a y‐intercept, assuming a mono‐exponential decrease. This y‐intercept is then considered to be S_tissue(b = 0), with minimal influence from blood perfusion. The detailed analysis of how this process excludes S_blood is provided in the Supporting Information. For the 50‐Hz OGSE signals from human livers, the maximum achievable b‐value is 0.3 ms/µm², due to hardware limitations. Fortunately, the IVIM effect on 50‐Hz OGSE signals is “invisible,” as explained later in the Discussion section. This allows us to use 50‐Hz OGSE signals acquired at very small b‐values (eg, 0.1 ms/µm²) directly, without excluding S_blood.

2.4. Model outcomes

The normalized signals were fit to Equation (3): as follows:

$$S_{\mathit{tissue}}\left(b,t_{\mathit{diff}}\right)=v_{\mathit{in}}\exp \left[-b\ast AD{C}_{\mathit{sphere}}\right]+\left(1-v_{\mathit{in}}\right)\exp \left(-b\ast D_{\mathit{ex}}\right)$$ (3)

using a nonlinear, constrained algorithm to generate cellular parameters (cell size d, intracellular diffusion coefficient D_in, extracellular parameters D_ex, and intracellular volume fraction V_in). We have found that different choices of D_in have only minor influences on the estimates of the other three parameters, with diffusion times ranging from 5 ms to 70 ms. ¹⁷ Therefore, D_in was fixed at 3 μm²/ms (the free water diffusion coefficient at 37°C) in our human study to reduce the number of fitting parameters, which better stabilizes the fittings of the other three parameters.

3. METHODS

3.1. In vivo quantification of hepatocyte size in mice and rats

3.1.1. Animal

All animal procedures were approved by the Institutional Animal Care and Use Committee at Vanderbilt University Medical Center. Three female Balb/c mice and three male Sprague‐Dawley rats (Harlan Laboratories, Indianapolis, IN) were studied.

3.1.2. In vivo preclinical MRI

The MR images were acquired with a Varian/Agilent DirectDrive horizontal 4.7T magnet (Agilent, Palo Alto, CA). A conventional PGSE sequence using pairs of monopolar diffusion gradients and an OGSE sequence using cosinusoidal diffusion waveforms acquired diffusion‐weighted (DW) data at relatively long and short diffusion times, respectively. Both OGSE and PGSE sequences were implemented using a respiratory‐gated, fat‐saturated, single‐shot EPI acquisition. The imaging parameters for PGSE acquisitions were diffusion gradient durations δ = 4 ms, and separation Δ = 10 ms and 40 ms. The OGSE sequence used gradient frequencies of 66 Hz and 100 Hz with δ/Δ = 15/20 ms and 10/15 ms, respectively, corresponding to effective diffusion times (1/4f, where f is the frequency) of approximately 3.75 ms and 2.5 ms. Five b‐values (0, 300, 500, 750, and 1000 s/mm²) were used for PGSE and 66.7‐Hz OGSE acquisitions. For 100‐Hz OGSE acquisitions, four b‐values (0, 300, 450, and 600 s/mm²) were used. Multiple axial slices covering the entire liver of each animal were acquired with a slice thickness of 2 mm. Other scanning parameters were TR = 3 seconds, matrix size = 64 × 64, FOV = 32 × 32 mm, and in‐plane resolution of 0.5 × 0.5 mm². Note that TEs of 70 ms for all diffusion measurements were the same, to minimize differential relaxation effects. The total scan time per animal was approximately 10 minutes.

Animals were anesthetized with a 2%/98% isoflurane/oxygen mixture before and during scanning. The rectal temperatures of animals were kept at 37°C using a warm‐air feedback system. Stretchable medical tape was used to ensure proper positioning of the mice and to restrain movements and reduce motion artifacts in the images. Respiratory signals were monitored using a small pneumatic pillow placed under the abdomen, and respiration gating (SA Instruments, Stony Brook, NY) was used to further reduce motion artifacts.

3.1.3. Histological validation

Immediately after each MRI session, animals were perfused intracardially with 0.1 mol/L phosphate‐buffered saline and formalin. The livers were then harvested and immersed in formalin for 24 hours. A single, 5‐µm‐thick liver tissue section was taken from each liver and stained with β‐catenin, a marker of hepatocyte membranes. The whole stained slides were scanned by a Leica SCN400 slide scanner with a magnification of ×20 to generate high‐resolution digital images (0.5 × 0.5 µm² per pixel). These high‐resolution images were divided into small subimages with size of 1000 × 1000 pixels, which matched the in‐plane resolution of MR images (0.5 × 0.5 mm²). A cell area–weighted average cell size and area fraction were recorded for each subimage using segmentation algorithms written in MATLAB. Maps of hepatocyte sizes and the intracellular area fractions for each section were generated.

3.2. In vivo quantification of hepatocyte size in healthy human subjects

3.2.1. Healthy volunteers

The human imaging studies were approved by the Institutional Review Board at Vanderbilt University Medical Center. Three healthy subjects were recruited, and their detailed descriptions can be found in Supporting Information Table S1.

3.2.2. Human MRI

The MRI was performed using a Philips Achieva 3T scanner (Amsterdam, Netherlands) with a dStream TorsoCardiac coil. A conventional PGSE sequence acquired data using pairs of unipolar diffusion gradients of duration δ = 12 ms and separation Δ = 74 ms. Shorter diffusion times were achieved using a cosine‐modulated trapezoidal OGSE sequence with δ/Δ = 40/52 ms. One‐gradient and two‐gradient cycles were used for 25‐Hz and 50‐Hz OGSE, respectively. Five b‐values (0, 250, 500, 750, and 1000 s/mm²) were used for PGSE with Δ =74 ms and 25‐Hz OGSE acquisitions. For the 50‐Hz OGSE acquisitions, four b‐values (0, 100, 200, and 300 s/mm²) were used. These diffusion parameters were chosen to meet the hardware requirements of clinical MR scanners and to ensure sufficient SNR for reliable IMPULSED fittings (eg, the duration of the OGSE waveform is limited by the length of the TE). Other imaging parameters were TR/TE = 4500/110 ms; FOV = 347 × 347 mm; reconstructed in‐plane resolution = 1.54 × 1.54 mm²; three slices; slice thickness = 10 mm; number of excitations = 2; respiratory‐gated, single‐shot EPI; SENSE factor = 3; and fat suppression with spectral‐attenuated inversion recovery. The total scan time was approximately 13‐15 minutes.

3.3. Data analysis

Liver regions of interest (excluding hepatic arteries and portal veins) were manually drawn on conventional T₂‐weighted images. The dependency of water diffusion on diffusion time, or gradient frequency, is the basis of assessing liver microstructure. For each voxel in the liver regions of interest, the signals acquired at b‐values of 0.2 ms/µm² or higher were tested to determine which of two possible models best fit their behaviors best. F statistics were used ³⁸ to determine whether a model with either constant or increasing ADCs (without any assumption of the increasing behavior) with decreasing diffusion times, or increasing oscillating gradient frequencies, is statistically more justified. Note that voxels with insufficient SNR favor the constant ADC model, because the noise tends to generate values of ADC that are very low. In practice, the F_ratio was calculated using the following expression:

$$F_{\mathit{ratio}}=\frac{S{S}_{model1}-S{S}_{model2}}{S{S}_{model2}}\frac{d{f}_{model2}}{d{f}_{model1}-d{f}_{model2}}.$$ (4)

Here, SS is the sum of squared deviations; df (= number of data points N – number of estimated parameters P) is the number of degrees of freedom; and model 1 and model 2 represent the constant and varying ADC models, respectively. The calculated F_ratio is then compared with a critical value of 9.5521, which is derived from an F table (the numerator has [df _model1−df _model2] degrees of freedom and the denominator has df_model2 degrees of freedom; 5% level of significance). If the calculated F_ratio value is less than 9.5521, the difference between the weighted sums of squared deviations is not significant; therefore, the varying ADC model represents the “best regression” according to the principle of parsimony. ³⁹

For voxels showing a reliable dependence of ADC on diffusion time, the DW signal curves acquired at b‐values of 0.2 ms/µm² or higher were extrapolated using a mono‐exponential model, and then divided by the resulting y‐intercepts to achieve diffusion decays with minimized IVIM effects. The IVIM‐free signals were then fit to Equation 3 to generate maps of mean cell size d, intrinsic intracellular diffusion coefficient D_in, intracellular volume fraction v_in, and extracellular diffusion coefficient D_ex, using a Bayesian probability theory–based grid search method, which is an optimal method for making inferences about data. ⁴⁰ , ⁴¹ The constraints for fitting parameters were based on physiologically relevant values ¹⁴ , ²⁶ , ²⁷ : 0 ≤ d ≤ 40 μm, 0 ≤ v_in ≤ 1, 0 ≤ D_in ≤ 3.0 μm²/ms, and 0 ≤ D_ex ≤ 3.0 μm²/ms. In a computer simulation study included in Supporting Information Figure S1, we demonstrated that the Bayesian analysis improves the accuracy and precision of parameter fittings (in particular, D_in) compared with traditional nonlinear regression approaches provided by MATLAB.

The precisions of the voxel‐wise parameter estimates were assessed by calculating the covariance matrix of the fitted parameters. ⁴² The RSD for each fitted parameter was estimated voxel by voxel following the approach described by Kellman et al for the purpose of T₁ mapping. ⁴³ , ⁴⁴ It has been shown in a phantom study ⁴³ that these estimated RSDs from a single measurement are equivalent to parameter variations obtained from multiple measurements.

4. RESULTS

4.1. In vivo quantification of hepatocyte size in mice and rats

Figure 1A shows the decay of DW signals when increasing b‐values for a single slice from a rat liver. The average y‐axis intercepts from mono‐exponential extrapolations of the large b‐value (≥ 0.2 ms/µm²) acquisitions, which equal 1−f_IVIM, are 0.58, 0.70, 0.94, and 0.98 (Supporting Information Figure S2B) for effective t_diff = 40, 10, 3.75, and 2.5 ms, respectively. The average ADC increases from 0.49 to 0.91 µm²/ms, with decreasing effective t_diff from 40 ms to 2.5 ms (Supporting Information Figure S2A). The DW signals were divided by their corresponding y‐axis intercepts to remove IVIM effects as explained previously. The average IVIM‐free signals were fit to Equation 3 to generate four cellular parameters (for this example, cell size d = 19.2 µm, V_in = 0.53, D_in = 1.6 µm²/ms, and D_ex = 1.3 µm²/ms).

FIGURE 1.

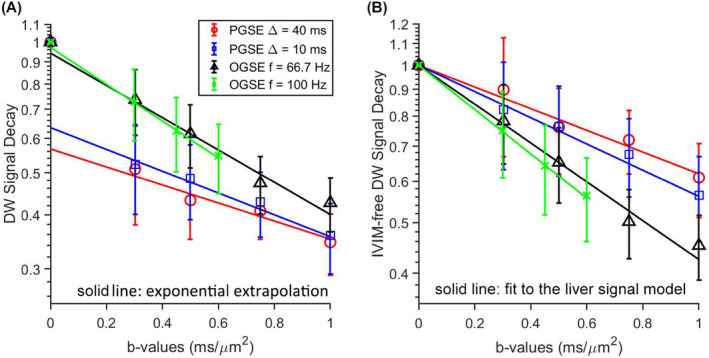
A, Normalized diffusion‐weighted (DW) signals for a single slice from a rat liver. The solid lines represent mono‐exponential extrapolations for the average signals acquired at b‐values of 0.2 ms/µm² or higher. B, The corresponding intravoxel incoherent motion (IVIM)‐free DW pulsed gradient spin echo (PGSE) and oscillating gradient spin echo (OGSE) signals. The solid lines represent fits using Equation 3

Figure 2A‐D shows the derived voxel‐wise parametric maps for a representative slice from a rat. Each of the parametric maps shows regional heterogeneity, which is not the same for each property. The voxel‐wise precision analysis (Figure 2E‐H) shows that the fitted cell size has a very low RSD (~6%), indicating high precision of voxel‐wise cell‐size mapping. The other three fitted parameters have an RSD of approximately 20%.

FIGURE 2.

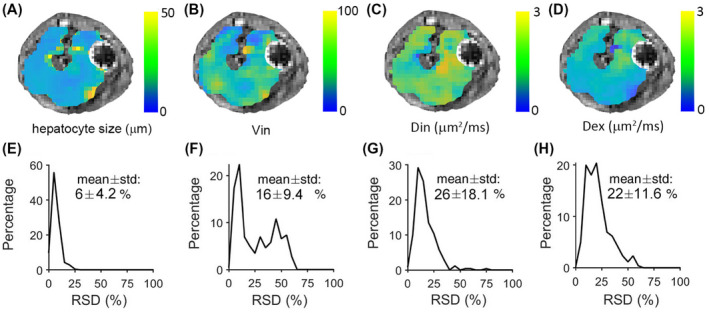
Parametric maps (A‐D) and histograms (E‐H) of voxel‐wise relative standard deviations (RSDs) of fitted cell size d, intracellular diffusion coefficient D_in, extracellular parameters D_ex, and ratio of V_in and V_ex, from a single slice of rat liver

We subsequently validated the MR findings by histology. Strong membranous β‐catenin staining in the liver allows us to segment hepatocytes easily and generate high‐resolution maps of hepatocyte size and cell area fraction (Figure 3). Histograms of MRI‐derived and histology‐derived hepatocyte sizes from the same rat liver have very similar profiles, as shown in Figure 4A. The MRI‐derived intracellular volume fraction has a lower mean value and wider distribution than that derived from histology (Figure 4B). Table 1 summarizes the IMPULSED and histology‐derived cell sizes and intracellular volume fractions from each rat and mouse liver, indicating that IMPULSED‐derived cell sizes show good agreement with histology, whereas IMPULSED‐derived intracellular volume fractions are lower than histological measurements.

FIGURE 3.

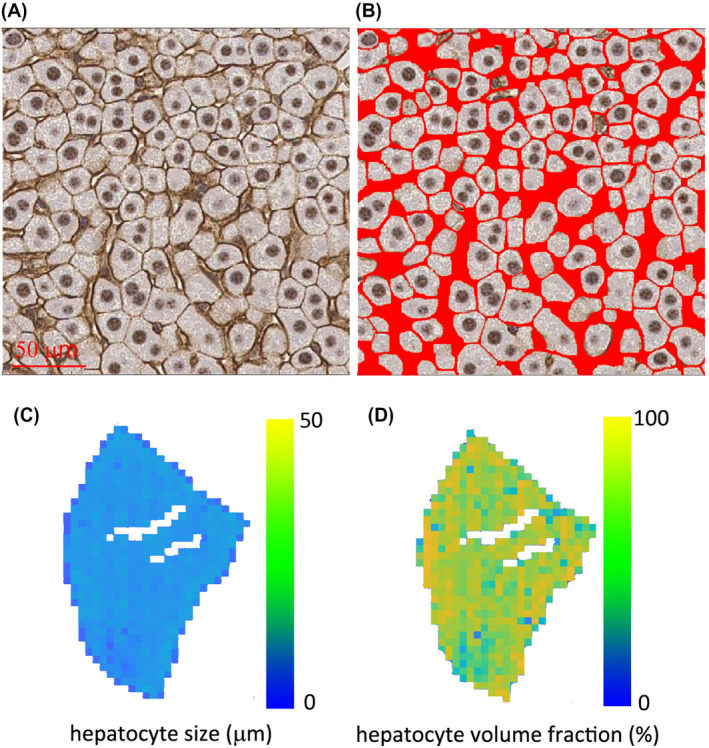
Histological analysis on a rat liver. A, Representative histological picture of β‐catenin‐stained liver tissues. B, Segmented hepatocytes with red color marking the extracellular spaces. Maps of hepatocyte size (C) and hepatocyte volume fraction (D) calculated from the segmented histological picture

FIGURE 4.

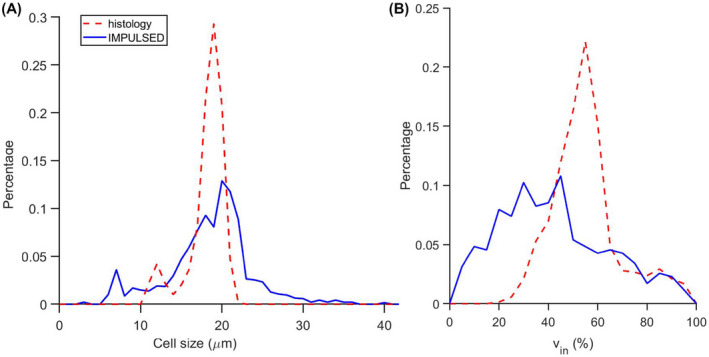
Histograms of IMPULSED (Imaging Microstructural Parameters Using Limited Spectrally Edited Diffusion) and histology‐derived hepatocyte sizes (A) and intracellular volume fractions (B)

TABLE 1.

Summary of IMPULSED‐derived and histology‐derived hepatocyte size and intracellular volume fraction (mean ± SD) for three rats and three mice

	Hepatocyte size (µm)		Intracellular volume fraction (%)
	IMPULSED‐derived	Histology‐derived	IMPULSED‐derived	Histology‐derived
Rat 1	19 ± 5.2	18 ± 3.0	48 ± 21.4	66 ± 16.5
Rat 2	18 ± 4.8	16 ± 2.0	42 ± 23.5	56 ± 16.7
Rat 3	16 ± 3.8	15 ± 1.9	45 ± 19.3	59 ± 14.2
Mouse 1	17 ± 4.1	18 ± 2.6	41 ± 26.2	60 ± 18.2
Mouse 2	16 ± 3.5	15 ± 3.1	47 ± 18.6	64 ± 16.3
Mouse 3	17 ± 4.2	16 ± 2.2	43 ± 16.6	55 ± 15.7

4.2. In vivo quantification of hepatocyte size in human subjects

Figure 5 and Supporting Information Figures S3 and S4 show IMPULSED‐derived parametric maps of mean cell size, intracellular diffusion coefficient, intracellular volume fraction, and extracellular diffusion coefficient of three continuous slices from three human livers overlaid on T₂‐weighted images. Hepatic arteries and portal veins were identified as hyperintense regions on T₂‐weighted images and then excluded from the liver regions of interest. The proportion of voxels that did not show a significant t_diff dependence of ADC, likely due to insufficient SNR and image artifacts, was less than 5% and were excluded from data fitting. Histograms of IMPULSED‐derived cellular parameters for 3 subjects are shown in Figure 6. The fitted average cell sizes are 17 ± 4.6, 16 ± 6.5, and 14 ± 6.1 µm for 3 subjects, respectively, consistent with reported human hepatocyte size ranges (~15‐25 µm in diameter). ¹⁹ , ²⁰ , ⁴⁵ The voxel‐wise precision analysis (Figure 7) shows that the cell size has the lowest RSD (~7%‐9%) among all four fitted parameters.

FIGURE 5.

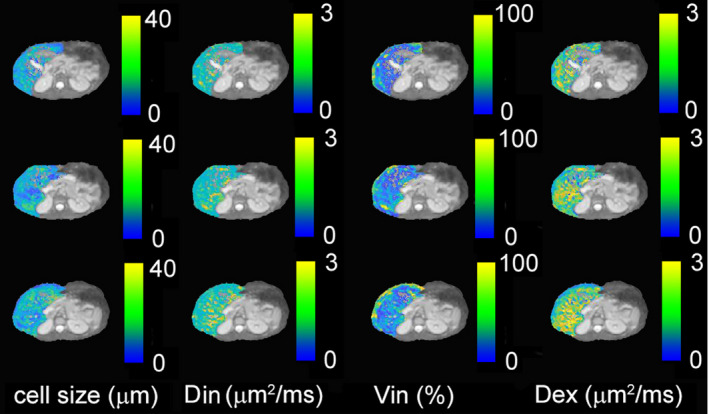
Parametric maps (cell size d, intracellular diffusion coefficient D_in, extracellular diffusion coefficient D_ex, and intracellular volume fraction V_in) for three continuous slices from healthy subject #1, overlaid on the corresponding T₂‐weighted images

FIGURE 6.

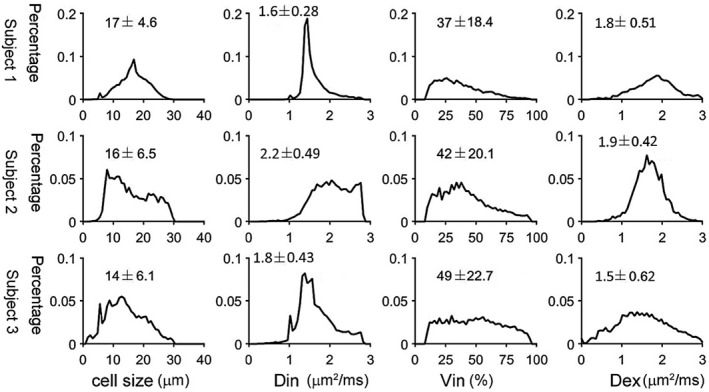
Histograms of IMPULSED‐derived cell size, intracellular diffusion coefficient D_in, intracellular volume fraction, and extracellular diffusion coefficient for 3 healthy human subjects

FIGURE 7.

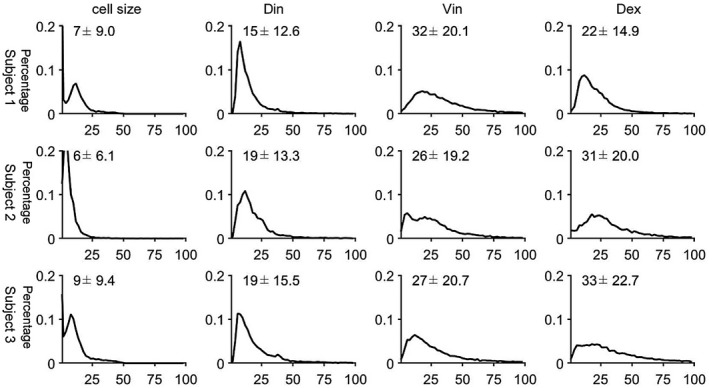
Histograms of RSDs of IMPULSED‐derived cell size, intracellular volume fraction, and extracellular diffusion coefficient for 3 healthy human subjects

5. DISCUSSION

5.1. Quantification of liver microstructure using the t_diff dependence and its applications

Using a combination of diffusion‐weighted acquisitions with different effective diffusion times, we measured the t_diff dependency in liver tissues over diffusion times from 2.5‐40 ms for rats and mice, and 5‐70 ms for human subjects. Previous studies in solid tissues, such as tumors, demonstrated that such a t_diff dependency provides a way to characterize microstructural features. In this study, we exploit a simple protocol previously introduced as IMPULSED, ¹⁵ , ¹⁷ which is capable of providing four microstructural metrics (ie, the cell size [or strictly, the restriction size] d, intracellular and extracellular diffusion coefficients [D_in and D_ex], and intracellular volume fraction v_in). To the best of our knowledge, this is the first study to demonstrate the feasibility of in vivo noninvasive assessment of hepatocyte size in animals and humans. The MR‐measured mean hepatocyte sizes in mice and rats are consistent with histology‐derived hepatocyte sizes, whereas the MR‐measured mean human hepatocyte size in healthy volunteers agrees with previous estimates from ex vivo measurements. In addition, hepatocyte size distributions from 2 human subjects showed apparent bimodal behavior, likely associated with hepatocyte polyploidization. Polyploidy is a characteristic feature of hepatocytes, which is an increase in the number of chromosome sets per cell. Enlarged cell size is the most obvious consequence of liver polyploidization. Different studies have reported that the volume of hepatocytes in human and mouse livers is approximately doubled with the doubling of DNA content. ⁴⁶ High polyploidization occurs as an aging‐dependent process. It has been reported that, for adult humans (20‐40 years old), the fractions of diploid and tetraploid hepatocytes are about 80% and 20%, respectively. ⁴⁷ , ⁴⁸ , ⁴⁹ , ⁵⁰ , ⁵¹ , ⁵² Because tetraploid hepatocytes are twice larger than diploid hepatocytes and IMPULSED‐derived cell size is volume‐weighted, it is plausible to observe bimodal distribution of hepatocyte size in adult humans. For adult mice and rats as used in this study (8‐12 weeks old), ⁴⁸ , ⁵³ the fractions of diploid and tetraploid hepatocytes are about 20% and 80%, respectively. The fact that IMPULSED‐derived cell size is volume‐weighted reduces the contributions from diploid hepatocytes and may lead to a single‐peak distribution of hepatocyte size, as observed in our animal study.

The fitted cell sizes have a high precision (RSD < 10%) when the baseline (b = 0) images have a SNR of 15‐20, suggesting that they can potentially be used to assess small changes in restriction sizes associated with pathological changes in the liver.

Death of hepatocytes is a characteristic feature of diverse liver diseases including cholestasis, viral hepatitis, ischemia, liver preservation for transplantation, and drug/toxicant‐induced injury. Cell death typically follows one of two patterns: oncotic necrosis or apoptosis. Cell shrinkage is one of the characteristic morphological changes that occur during the early process of apoptosis. During later stages, cells separate into several apoptotic bodies. Cellular death due to necrosis results in the loss of cell membrane integrity and an uncontrolled release of cellular contents into the extracellular space. Although such changes might hinder extracellular water movement, necrotic bodies and fragments of cellular debris are too small to influence the cell‐size measurements in the regime of interest, as IMPULSED emphasizes the effects of restrictions in a specific size range (eg, 5‐20 μm in this study). Thus, water diffusion in necrotic/late apoptotic regions appears to be relatively “unrestricted,” and the corresponding ADC values do not show significant diffusion‐time dependency within the diffusion time range we used in the current study. Determining the t_diff dependence of ADC could be an effective way to differentiate necrosis/late apoptosis from healthy hepatocytes and/or early‐stage apoptotic hepatocytes.

Hepatocellular ballooning, the key diagnostic feature of nonalcoholic steatohepatitis, can be evaluated only by grading histological specimens obtained from invasive biopsies with a score of 0, 1 or 2, corresponding to “absent,” “few,” or “frequent.” It is usually defined as rounded hepatocyte enlargement more than 1.5‐2 times the normal diameter. ⁴⁷ The range of volume fractions of hepatocytes undergoing “ballooning” has to our knowledge never been reported. If we assume that the volume fraction of hepatocytes undergoing ballooning is 20%, then we can estimate that the average hepatocyte size increases between 14% and 34%. Given the low value of the SDs of our fitted values, we expect that increases in cell size associated with ballooning could be detected by our method in subjects with relatively low levels of affected cells. In addition, accumulation of fat lipids in ballooned hepatocytes may decrease water‐diffusion rates and therefore lead to a decreased intracellular diffusivity D_in.

In other conditions, liver cancer cells (10‐15 µm) and mononuclear infiltrates (6‐10 µm) may also make significant contributions to the estimated average length scale. Therefore, assessing changes in the average length scale may also play a role in the diagnosis and treatment‐response monitoring of focal and diffuse liver diseases.

The liver tissue model analyzed includes other cellular properties, including intracellular and extracellular diffusion coefficients, and intracellular volume fraction. Our animal study showed that IMPULSED‐derived intracellular volume fractions are smaller than those estimated from histology. Our signal model ignores water exchange between intracellular and extracellular spaces, which has been shown to be reasonable in previous OGSE studies. ³⁴ , ⁵⁴ Ignorance of membrane permeability values is likely to underestimate the fitted intracellular volume fraction without affecting the accuracy of cell‐size measurement. ¹² , ¹³ The influence of transcytolemmal water exchange (characterized by the intracellular water life time τ_in, which reportedly may vary from about 50 to 150 ms) on quantitative measurements of tissue properties has been investigated previously using diffusion MRI, including IMPULSED and other PGSE methods. Intracellular volume fraction v_in was intrinsically underestimated by IMPULSED and decreased rapidly with shorter τ_in, whereas mean cell diameters were estimated accurately independent of transcytolemmal water exchange with sufficient SNR (eg, 50). These findings support our observations that hepatocyte sizes were estimated accurately, whereas intracellular volume fraction v_in was significantly underestimated. Establishing a quantitative relationship between the magnitude of membrane permeability and bias of v_in estimation could potentially assist in developing a new imaging marker for detection of changes in membrane permeability in different liver pathologies.

It is challenging to obtain the true values of intracellular and extracellular diffusion coefficients. The variations of these parameters are about 15%‐30%, as shown in Figure 7. Therefore, caution is needed to interpret associated changes in these parameters in terms of pathological changes in liver microstructure. On the contrary, the parameter variations can be decreased by increasing SNR, which typically requires longer scanning time.

5.2. Removing IVIM effects

Our previous cancer studies of measuring cell sizes in solid tumors ignored the influences of blood. ¹² , ¹³ , ¹⁷ However, in this liver study, we found that removing IVIM effects is crucial to extract cellular properties of liver tissues, not only because the blood perfusion volume fraction is larger in the liver than that in many tumors, but also because of the t_diff dependence of IVIM effects. We showed that the IVIM effects on PGSE and OGSE measurements decreased with decreasing t_diff for both animal and human livers. Similar observations have been reported in mouse brain by Wu et al ³⁷ and in the human liver and pancreas by Wetscherek et al. ⁵⁵ As explained by Wu et al, ³⁷ PGSE measurements using relatively long diffusion times are significantly affected by microcirculatory flow, which passes through multiple vessel segments during t_diff, which attenuates DW signals exponentially with a rate of D^* (~10 times higher than the tissue water diffusion coefficient). In contrast, OGSE signals with f ≥ 50 Hz are affected only by microcirculatory flow that stays in the same vessel segment during t_diff, which attenuates DW signals exponentially with D_blood, the self‐diffusion coefficient of the water molecules in the capillary blood. In this study, we removed the effect of D^* by extrapolating signal curves acquired at b‐values of 0.2 ms/µm² or greater with a mono‐exponential model. Because D_blood is close to the tissue‐water diffusion coefficient, ⁵⁶ we assumed that D_blood(t_diff) equals the tissue‐water ADC at the same t_diff to simplify our fitting procedure. The fitted hepatocyte sizes in mice, rats, and humans were consistent with literature values and histological analyses, suggesting that our assumption is reasonable. To differentiate the small difference between D_blood and tissue water ADC, high b‐value data with sufficient SNR are needed. Therefore, including D_blood as an independent variable in the fitting model may potentially lead to a more accurate quantification of liver cellular properties, but at a cost of increasing scanning time.

5.3. Limitations

There are limitations to this study. The fitted cell size represents the average restriction size in each imaging voxel, which might lower the sensitivity of IMPULSED for assessing changes in a certain type of cells. Further efforts to estimate the cell‐size distribution are ongoing. However, one important point should be kept in mind: The more complicated the signal model becomes, the higher SNR that is required to obtain stable fittings. The SNR improvement is usually made at a cost of either increasing scanning time (eg, more acquisitions) or losing spatial information (eg, region of interest–based quantitative analysis), and therefore needs to be examined on a case‐by‐case basis.

A second limitation is that only healthy animals and humans were studied. Fat accumulation has been considered a significant risk factor for various liver diseases, so a feasibility study of IMPULSED in fatty liver tissues is of considerable importance. Image artifacts caused by imperfect fat saturation have been reported to affect quantitative MRI analyses. Fortunately, fat diffusion rates are two orders of magnitude lower than for water diffusion. ⁶ With the diffusion times we used in this study, lipid molecules move a very small distance (<1 µm) and experience “free diffusion” inside hepatocytes. With the maximum b‐value that we used (1 ms/µm²), the unsaturated fat signal decays about 1%, and therefore can be included as a constant term in the liver signal model. Further research validating this hypothesis is ongoing. In addition, a small number of rodents were used without formal sample‐size calculation, because the main goal of this study is to demonstrate the feasibility of in vivo assessment of hepatocyte size in animals and humans. Instead of performing strict statistical analysis, we listed the cell sizes (mean ± SD) measured by IMPULSED and histology for each animal (Table 1), indicating that our MR findings are physiologically reasonable. We have been actively engaged in further animal studies investigating the precision and accuracy of IMPULSED‐derived cell sizes.

Due to the challenges in the co‐registration between histology and in vivo MRI of deformable rodent livers, for each animal, histology‐derived parameters from a section of liver were compared with MRI‐derived parameters from the entire liver in the current work. This may lead to a narrow distribution of histology‐derived parameters compared with those measured by the IMPULSED method. For even better accuracy, it is plausible to perform a voxel‐wise correlation between histology and ex vivo MRI of liver samples in future studies.

The precision of each derived parameter was assessed by estimating the covariance matrix of the fitted results. The voxel‐wise RSD of each fitted parameter was estimated by computing the covariance matrix for the signal model parameters by inverting a first‐order approximation to the parameters’ Hessian matrix. This approach has been used to assess the precision of T₁ mapping. ⁴³ , ⁴⁴ In a phantom study, ⁴³ it has been shown that these estimated RSDs from a single measurement are equivalent to variations obtained from multiple measurements. In this study, RSD values were provided to shed light into the repeatability of the parameter estimates. However, the RSD value provides information only regarding the random error and does not in itself provide any information on systematic bias errors (eg, susceptibility artifacts that may be different between MRI scans on the subject). Therefore, our next step is to evaluate the repeatability of each parameter by comparing their values from different scans on the same subject.

Bulk liver motion (eg, nonrigid motion of a voxel imparted by the motion of the heart) introduces extra phase dispersion in liver DWI signals, particularly in the left lobe, which biases conventional quantitative diffusion analyses, such as estimates of ADC. ⁵⁷ The IMPULSED protocol uses a combination of PGSE and OGSE sequences. The OGSE sequence uses flow‐compensated diffusion gradients and allows motion‐robust diffusion signals. We will use flow‐compensated PGSE sequences to further minimize motion effects in IMPULSED protocols.

6. CONCLUSIONS

We introduce a noninvasive, clinically feasible, diffusion‐based MRI approach for mapping hepatocyte size in livers. Different from conventional diffusion MRI, this approach is based on the TDS framework that uses different diffusion gradient temporal waveforms to achieve a broad range of diffusion times from about 2.5‐70 ms for characterizing microstructure more comprehensively. In preclinical validation studies using mice and rats, IMPULSED‐derived microstructural parameters such as hepatocyte size agreed well with histological findings with the removal of blood microcirculation effects. We also conducted a feasibility study to show that IMPULSED can characterize hepatocyte size in human subjects with a clinically feasible scan time on a clinical 3T MRI scanner. This study demonstrates the first attempt for imaging hepatocyte size in vivo and opens an avenue for characterizing histopathological information in livers noninvasively, which could have clinical potential in diagnosis and monitoring therapeutic response of various liver diseases.

Supporting information

FIGURE S1 Evaluation of accuracy and precision of fitted parameters (d, v_in, D_in, and D_ex) using two fitting algorithms, including traditional nonlinear regression provided by MATLAB R2018b (function name: fmincon) and in‐house‐developed Bayesian probability theory‐based grid search method

FIGURE S2 Box and whisker plots of ADC (A) and 1−f_IVIM (B) values at different diffusion times/oscillating gradient frequencies, obtained by fitting a mono‐exponential decay to the relatively high b‐value signals (≥0.2 ms/µm²) for a single slice from a rat liver. The 25th‐75th percentiles are blocked by the box. The band inside the box is the mean, and the whiskers mark the minimum and maximum values

FIGURE S3 Parametric maps (cell size d, intracellular diffusion coefficient D_in, extracellular diffusion coefficient D_ex, and intracellular volume fraction V_in) for three continuous slices from healthy subject #2, overlaid on the corresponding T₂‐weighted images

FIGURE S4 Parametric maps (cell size d, intracellular diffusion coefficient D_in, extracellular diffusion coefficient D_ex, and intracellular volume fraction V_in) for three continuous slices from healthy subject #3, overlaid on the corresponding T₂‐weighted images

TABLE S1 Information on human subjects

Jiang X, Xu J, Gore JC. Mapping hepatocyte size in vivo using temporal diffusion spectroscopy MRI. Magn. Reson. Med. 2020;84:2671–2683. 10.1002/mrm.28299