Figure 6.
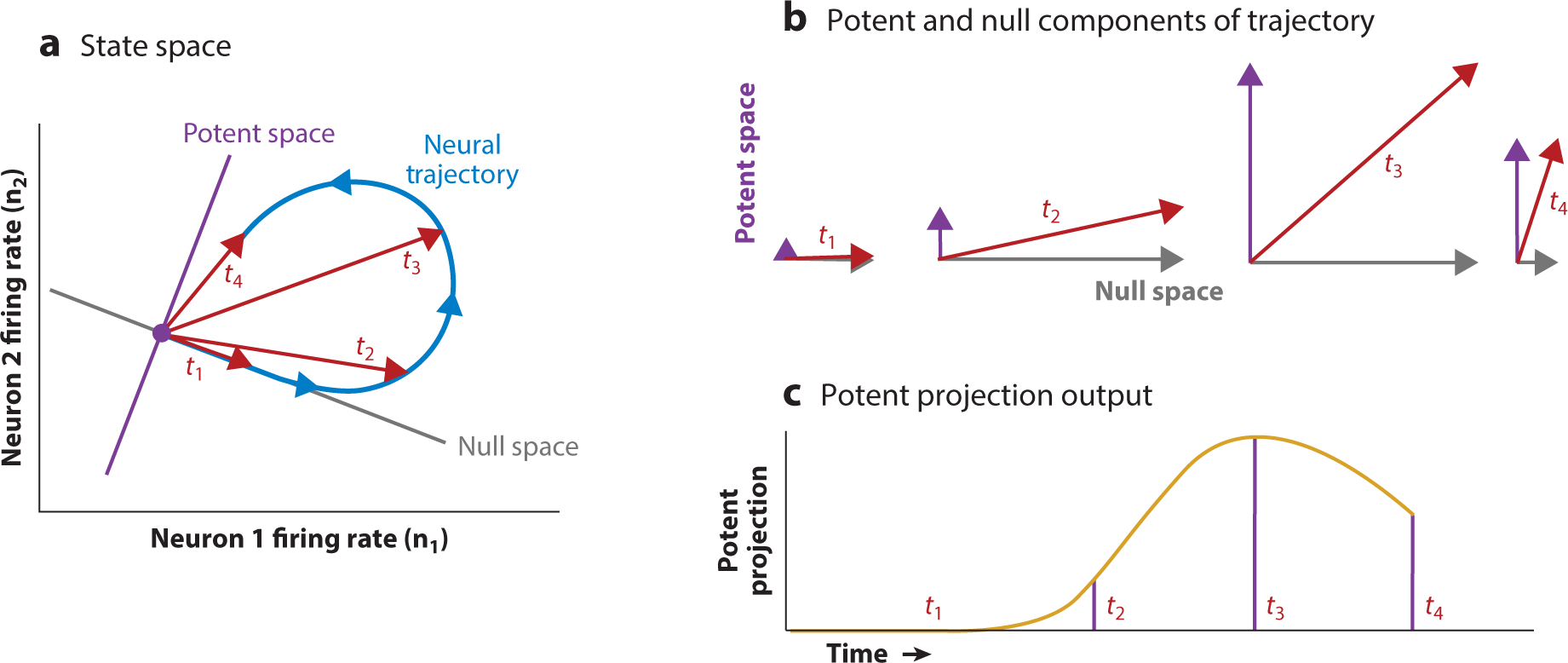
Null and potent subspaces. A state space can be divided up into nonoverlapping subspaces, called the potent and null (sub)spaces, where the potent space may be read out by a downstream area, while the null space is not read out. (a) A dynamical trajectory (blue arrows) in state space follows a looping dynamic from the origin back to the origin. While doing so, the trajectory has projections on the null space (gray line) and potent space (purple line). We focus on four points in time, t1, t2, t3, and t4 (red arrows). (b) The state space trajectory in panel a can be decomposed into its projections onto the potent and null spaces (shown for time points t1, t2, t3, and t4). (c) The projection of the state space trajectory onto the potent dimension through time (yellow line), highlighting its value at time points t1, t2, t3, and t4. There is a corresponding time series for the projection onto the null space (not shown), but this is not read out by a downstream area. Examples of this in systems neuroscience can be found in these references (Hennig et al. 2018, Kaufman et al. 2014, Perich et al. 2018, Semedo et al. 2019, Stavisky et al. 2017a).
