Improving practices and inferences in developmental cognitive neuroscience

Abstract

The past decade has seen growing concern about research practices in cognitive neuroscience, and psychology more broadly, that shake our confidence in many inferences in these fields. We consider how these issues affect developmental cognitive neuroscience, with the goal of progressing our field to support strong and defensible inferences from our neurobiological data. This manuscript focuses on the importance of distinguishing between confirmatory versus exploratory data analysis approaches in developmental cognitive neuroscience. Regarding confirmatory research, we discuss problems with analytic flexibility, appropriately instantiating hypotheses, and controlling the error rate given how we threshold data and correct for multiple comparisons. To counterbalance these concerns with confirmatory analyses, we present two complementary strategies. First, we discuss the advantages of working within an exploratory analysis framework, including estimating and reporting effect sizes, using parcellations, and conducting specification curve analyses. Second, we summarize defensible approaches for null hypothesis significance testing in confirmatory analyses, focusing on transparent and reproducible practices in our field. Specific recommendations are given, and templates, scripts, or other resources are hyperlinked, whenever possible.

As developmental cognitive neuroscientists, we share a common goal of being able to draw strong, defensible, reliable inferences from our neuroimaging data. Several issues have recently come to light that have prompted introspection across the field regarding certain research practices. Some of these issues have impacted the field of psychology in general, while others are specific to cognitive neuroscience and various neuroimaging techniques. These issues include, but are not limited to, differentiating between hypothesis-driven and exploratory research (de Groot, 2014; Gelman and Loken, 2013), performing the correct statistical tests (Nieuwenhuis et al., 2011), correcting for multiple comparisons (Eklund et al., 2016), following standard reporting procedures (Nichols et al., 2017), and evaluating reproducibility1 (Gorgolewski and Poldrack, 2016). We argue that these issues require ongoing and focused attention, as they affect the foundation upon which we are able to draw defensible inferences from the research we conduct. Other groups have produced recommendations for concrete steps to address many of these concerns (such as Poldrack et al., 2017), but here we highlight issues of special relevance to developmental cognitive neuroscience (DCN), with examples drawn from our own experience with functional magnetic resonance imaging (fMRI, including both task and resting-state; note, however, that this method shares many relevant features with other imaging modalities).

The core argument of this paper is that, under the field’s dominant paradigm for statistical inference (null-hypothesis significance testing; NHST), being mindful of the differences between confirmatory and exploratory approaches is necessary to ensure our inferences are sound, and will facilitate significantly improved research practices. We will not argue for abandoning statistical significance testing (McShane et al., 2019), but proceed in line with authors who argue that NHST, used correctly, can be a useful part of testing hypotheses and theories (Benjamin et al., 2018; Lakens, 2019; Lakens et al., 2018; Mayo, 2018); we also acknowledge that there are other valid ways to make scientific progress but limit the scope here to NHST. There are intense pressures to “publish or perish,” and with that comes the potential for both overreliance on and inadvertent misapplication of confirmatory techniques. However, we contend the field is still early enough in its own development to dramatically benefit from comprehensive descriptive and careful exploratory research that will lay more solid and reproducible groundwork for future confirmatory research (a stance well articulated by Rozin, 2001). As such, we will advocate approaches that protect the validity of inferences from confirmatory NHST, and that may overcome limitations of NHST applied in exploratory analyses.

This paper is organized into four major sections. The first section provides a brief introduction to inference using NHST and distinguishes confirmatory and exploratory approaches2 . The second section tackles issues of particular importance to confirmatory approaches, including appropriately instantiating hypotheses in statistical tests, properly controlling error rates for analytic flexibility and multiple comparisons in mass univariate data, as well as misuses of p-values. The third section outlines exploratory approaches, which provide promising solutions to some of these concerns, including calculating and reporting effect sizes, using parcellations, and conducting specification curve analyses. The final section concludes by summarizing practices that support transparent and reproducible research in DCN, highlighting their importance to protecting the integrity of confirmatory analyses (although transparency is also crucial for maximizing the interpretability of exploratory research as well).

1. Introduction to inferential pitfalls

The vast majority of DCN research is conducted within a confirmatory null hypothesis significance testing (NHST) framework, wherein the p-value of a statistical test, in conjunction with a decision rule, leads us to reject or not reject a specific null hypothesis, and thereby draw some conclusion that has some bearing on our target theory (the connection between this decision rule and the evidential value of a test is a topic of ongoing philosophical debate; Mayo and Spanos, 2011; Mayo, 2018). For example, in an fMRI experiment, we might compute a statistic at each voxel to evaluate the difference in BOLD response between some set of conditions or groups; develop a combined magnitude and extent threshold to ensure our cluster-wise error rate is less than 5%; discover some set of contiguous voxels above that threshold; and so decide to conclude that there is a real effect in that cluster that is important for understanding differences between psychological processes or group characteristics. In this article, we present issues related to confirmatory research that deal with real and common threats to the quality of inferences made from these kinds of testing procedures. While there are other inference problems in cognitive neuroscience, such as reverse inference in which one infers that a specific psychological process is occurring after observing activity in a specific region (Poldrack, 2006), the threats discussed here are largely the result of how one uses the p-value to make a null-rejection decision (see, e.g., Greenland, 2019). To make this decision correctly, we need to understand what gives p-values their meaning with respect to an a priori alpha level set to control the false positive error rate, and when and how that meaning changes.

The central ideal behind the p-value is that if a given null hypothesis is true, and if the same procedure (from sampling to statistical analysis) is repeated over and over, certain results should occur only rarely. Customarily, we decide to reject the null hypothesis if we can be sure that we will do so mistakenly only 5% of the time if it is really true (i.e., alpha = .05). When we correct for multiple comparisons, we are ensuring that for a whole set of comparisons (say, a comparison at every voxel or in the case of structural MRI, at every vertex), we will only reject the null hypothesis for a single voxel in the whole brain just 5 % of the time if in fact the null hypothesis is true at that voxel. Crucially, knowing this error rate rests on our ability to define exactly (i) what procedure we would be repeating (i.e., deploying across study replications)—as mentioned before, from sampling to analysis—and if we are correcting for multiple hypothesis tests, (ii) exactly how many hypothesis tests arise as part of that procedure (de Groot, 2014; Gelman and Loken, 2013; Gelman and Loken, 2014). Serious threats to inferences based on p-values occur when we deviate from that procedure.

For each data-contingent deviation from that procedure (that is, any decision not made prior to seeing the data), we can only adequately control our error rate if we correct for both the decisions we did make and also those we might have made had the data been just a bit different, guiding us in another direction. Some examples of such decisions are likely obvious, such as examining interactions between predictors of interest (e.g., age ✕ sex) when the main effect analysis does not yield significant results. The fact that many other decisions also cause problems is less clear, such as determining quality control criteria for exclusions after examining motion or preprocessed images, or log-transforming a variable of interest after observing its distribution. Each of these decisions is contingent on the data one has, and so might be made differently in a replication. Such deviations from planned analysis pipelines can result in an unknowable number of possible tests, and without knowing how many possible tests one could perform, one cannot know and appropriately correct for the probability of false positives for tests across all possible replications. Importantly, as described by Gelman and Loken (2013, 2014), making a single deviation leads to a “garden of forking paths” producing an unknowable number of possible deviations (had the data or researcher's choices been slightly different) and thus invalidates the p-value as a statistic that helps us control our false positive error rate. The fact that a single unplanned analytic decision may lead to an unreconcilable multiple-comparisons problem may come as a shock to many DCN researchers who have, like us, almost certainly drawn conclusions based on analyses that were not fully pre-specified (or otherwise appropriately corrected). Clearly, this fact has profound implications for how we view much of the extant literature in our field, as is now quite widely acknowledged (John et al., 2012; Klein et al., 2018; Simmons et al., 2011).

These insights about the basis of our inferential procedures reveal the need to draw a bright line between exploratory and confirmatory analyses when operating under NHST as a statistical framework. In contrast to confirmatory data analysis, exploratory research is characterized by the goal of hypothesis generation, and should involve rigorous, structured, and systematic investigation of a phenomenon (Devezer et al., 2020; Rozin, 2001). Crucially, exploratory research cannot simply be a label for the improper application of significance testing. Prominent conceptualizations of exploratory data analysis characterize this approach in various intersecting ways, ranging from model-free graphical visualizations that allow identification of unexpected patterns in the data, to descriptions of ways in which fitted models depart from data (Gelman, 2003; Tukey, 1977). It has become more feasible than ever to exhaustively explore one’s data with the evolution of statistical and neuroimaging programs and especially pipelines like fmriprep (Esteban et al., 2019) and fitlins (Markiewicz et al., 2019), but the extent to which this diverges from a confirmatory approach may not have been readily apparent. In our opinion, exploratory research is a boon to science, to the extent that it is not confused with or allowed to contaminate confirmatory analyses. We think that maintaining boundaries between confirmatory and exploratory research will be enhanced by encouraging more rigor in the former, and recognizing the value of the latter. Both of these will be covered in turn below.

2. Confirmatory analyses

There are a number of common practices in DCN that negatively impact the utility of p-values as an inferential tool in confirmatory data analysis. Although some of these practices are common to the field of psychology more generally, others represent neuroimaging-specific challenges that compound issues of inflated type 1 error, such as the multitude of pre-processing steps and methods for correction for multiple comparisons.

2.1. Reducing analytic flexibility

In the field of psychology, it is well established how “researcher degrees of freedom” (J. P. Simmons et al., 2011) provided by the extensive number of analysis decisions in scientific research can present an endless “garden of forking paths” (Gelman and Loken, 2013). We focus here on imaging-specific decisions that can produce problematic analytic flexibility. In neuroimaging research, there are myriad decisions made along the path from DICOMS to results (Wicherts et al., 2016). Across multiple approaches to analyzing fMRI data, we must make decisions about things like statistical modeling approach, smoothing kernel, high-pass filter, autocorrelation modeling approach, quantification of motion and other nuisance regressors, scrubbing or censoring volumes, selecting seeds or parcellation schemes for connectivity measures, and manner of correcting for multiple comparisons, to name just a few. While in the vast majority of cases, we ultimately decide and report on one specific method in our manuscripts, there might have been significant pre-publication investigation into the effect of differing parameters or methods during the analytic process, or decisions that were plausibly influenced by knowledge about some aspect of the data. This analytic flexibility is often unaccounted for in the final results, resulting in inadequate correction for type 1 error (Carp, 2012). However, it also creates a dilemma as many of us are still trying to better understand the impact of these (seemingly small) decisions within a relatively new and constantly evolving field. This analytic flexibility also results in substantial variability in researchers’ conclusions even when analyzing the same data-set (Botvinik-Nezer et al., 2020), which bodes poorly for replication.

One pertinent example specific to neuroimaging is provided by region of interest (ROI) analysis. Researchers with hypotheses focusing on specific regions can investigate ROIs in a multitude of manners. Firstly, ROIs can be used as a mask to constrain the whole-brain search space, or they can be used to extract summarized parameter estimates and conduct statistical analyses in non-imaging software programs. For both of these approaches, ROIs can be defined in various ways including by structure or function, with many options within each method (e.g., Harvard-Oxford atlas versus Desikan-Killiany atlas, diameter of functional spheres, entire clusters, or use of functional localizers, independent samples, or meta-analyses). Even if ROIs are based on prior literature, there may be variation with respect to the location or boundaries of regions named identically. This presents a large number of researcher degrees of freedom that can threaten inferences based on p-values if an ad hoc investigative approach is taken. A related issue is that for arguments regarding the specificity of an effect within an ROI, one or more comparison regions must also be defined. Together, these examples illustrate the necessity of detailed plans, such as those specifying exactly how ROIs will be defined, to usefully identify the extent of analytic flexibility such that one can appropriately constrain the false positive error rate as discussed above. Such plans also increase the spatial specificity of neuroimaging hypothesis, further reducing researcher degrees of freedom (Hong et al., 2019).

One strategy that has been used for some time in fields that test clinical interventions is the public registration of research plans, e.g., at the National Institutes of Health public registration database (clinicaltrials.gov). This has also been adopted broadly in social and personality psychology via tools, e.g., at https://OSF.org and https://aspredicted.org. Since the research plan is transparently disseminated prior to conducting research, those interpreting the results can be assured that the outcomes of these clinical trials, based on the NHST principles discussed above, are correctly conditioned on the number of comparisons performed. This strategy is one of several possible solutions to the problem of forking paths (Rubin, 2017). It works well when the correct analytic plan is known and can be specified a priori, and when the data are unlikely to deviate in surprising ways from the assumptions of that plan. However, preregistrations may be a particularly brittle solution in that a misspecified analysis plan will produce biased estimates, yet deviations (e.g., to correct the revealed misspecification) introduce the very analytic flexibility they are meant to eliminate (Devezer et al., 2020). Other possible solutions include adjusting the alpha level of preregistered analysis plans to account for specific conditional possibilities (see section 2.4 for a discussion of this problem with regard to massively univariate neuroimaging data and 4.1 for further detail on preregistration), and sensitivity analyses (see section 3.3 in which we discuss specification curves as an exploratory method).

2.2. Ensuring observations and hypotheses are correctly linked

Another issue in confirmatory research is ensuring that we correctly instantiate our hypotheses and make inferences from the appropriate statistical tests of them. Whereas the above-described analytic flexibility leads to unknown error-rate inflation, the inferential statistics in the present section may have correctly controlled error-rates, but their bearing on the hypothesis is unclear or incorrect. Interaction hypotheses represent a common example of accidental failures in this regard. DCN research questions typically examine complex relationships between multiple variables, and the associated statistical models frequently involve tests of interactions. For example, if analyzing whether developmental differences (e.g., adolescents versus adults) in neural activation produced by affective facial expressions vary by emotion (e.g., angry, happy, and sad conditions), a significant interaction between group and condition in a 2 × 3 ANOVA would provide support for rejecting the null hypothesis. However, even if this test statistic is non-significant, it is common practice to examine simple effects (i.e., neural activation within each age group and condition separately), which is important for fully characterizing developmental patterns as well as facilitating future research and meta-analyses.

However, a problem arises if the p-values of simple effects tests are inappropriately used to support the interaction hypothesis; in other words, identification of significant age group differences for one emotion but not the others may be incorrectly discussed as a rejection of the null interaction hypothesis (e.g., claiming that there is an age difference in neural responses that is unique to one emotion), even though the necessary analysis (the interaction test) suggested otherwise. While this issue is not specific to development or neuroimaging, and has been raised before (Nieuwenhuis et al., 2011), we highlight this problem given that (i) it is persistent, and (ii) our desire as developmental scientists to compare age groups might increase the tendency to inadvertently engage in these practices. In confirmatory research, careful consideration needs to be given to identifying the specific statistical test that instantiates a given hypothesis, which will also ensure that we are appropriately interpreting the meaning of p-values.

2.3. Some misuses of p-values

While limiting analytical flexibility as well as selecting and reasoning from appropriate statistical tests are both critical to a confirmatory approach, it is also vital to recognize the inferential limitations of how we typically use p-values. Notable misuses are briefly discussed below along with recommended solutions.

First, failing to reject the null hypothesis of no difference does not imply that there is no actual difference. It is possible to fail to reject the null when it is in fact false—that is, when there really is a true effect—because, for example, the size of the effect is too small to be detected using the given methodology due to imprecise measurement or small sample size. The probability of failing to reject the null when it is false (a type 2 error) is equal to beta, and 1-beta is equal to power. In what is conventionally considered a well powered study, there is a good chance (10–20 % for some effect size of interest) of failing to reject the null even when there is a true effect. It is quite possible that the average study in our field has even lower power to detect effects of a magnitude we might care about, though this is difficult to determine as we are not used to considering what might be the smallest effect we would be interested in, in part because effect sizes in neuroimaging work are infrequently reported.

The mistake of accepting the null as true when it is not rejected is especially pernicious in the interpretation of whole-brain statistical parameter maps that anchor many fMRI papers (e.g., voxel-wise, seed-based connectivity, psychophysiological interactions). When interpreting the spatial distribution of significant effects, it is crucial to keep in mind two things. One, outside of highly powered studies, we cannot interpret the lack of a statistically significant cluster in some region as evidence that there is no true underlying effect in that region. In short, we can only use the kinds of p-values we typically generate to infer that there is some effect in certain clusters—everywhere else there may be a true effect that we were simply underpowered to detect. Two, our thresholding procedures may give the impression that one region does not show an effect while the other does, despite the possibility that the effects would not be significantly different if voxels were statistically compared to each other (Jernigan et al., 2003). In other words, we are making an inference that would require support from a significant interaction, without ever testing that interaction directly (see section 2.2 above). For example, we typically infer cortical midline structures support self-referential processing because of the presence of significant clusters in those regions and absence of significant clusters in much of the rest of the brain during a contrast between self-reference and a control condition, but we have never statistically tested this.

There do exist principled methods for deciding in favor of the null hypothesis, though this has rarely been applied in the neuroimaging literature. Two approaches are becoming common in NHST. First, one may decide a priori to define a certain range of values that are too small to be of practical significance, and then perform a statistical equivalence test that can be used to reject the hypothesis that the true value is outside of this range, for example, by using two one-sided tests (TOST; Lakens, 2017). In an fMRI analysis, the p-values from this procedure (i.e., the highest of the two tests) could conceivably be generated across the whole brain and corrected using an appropriate FWE correction method. Second, one may appeal to the expected false-negative rate for some value deemed to be of minimal practical significance, which can be computed as 1 - power for detecting that effect size using a NHST. This argument for deciding that the null hypothesis is true via the false-negative error rate mirrors the inferential logic of NHST based on the controlled false-positive rate, though, this may be complex given the aforementioned lack of attention to effect sizes. The neuroimaging literature would be bolstered by future work exploring these procedures.

Finally, and related to the first limitation, rejecting the null hypothesis of no difference does not provide information about whether an effect is meaningful or not. Recent disputes over the effect of digital technology use on adolescent well-being in large, nationally representative studies have illustrated how easy it is to assume a significant effect is consequential (Orben and Pryzbilski, 2019b). With the increase of DCN studies around the world of similar scope, it is crucial that we develop ways of communicating not only the statistical significance of a finding but also the size of its effect relative to other effects of interest. Many standardized effect size metrics exist, such as Cohen’s d, the Pearson’s correlation coefficient, and 2. While these familiar measures are potentially comparable across studies, they do not anchor the effect size in the phenomenon of interest (but rather in the observed variance of the measured constructs) and are often more challenging to interpret than simple effect sizes, such as mean differences (Baguley, 2009). They may thus be supplemented by an alternate approach that compares the observed effect size to an effect that may be expected for a clinically significant difference in the outcome. For example, in a study examining the relationship between early life stress, resting-state connectivity, and anxiety, authors could use median scores for clinical versus non-clinical presentations of anxiety to anchor the corresponding model-expected differences in connectivity. Such a study might report that the average connectivity difference (within some network) between individuals with and without a history of early adversity is associated with an increase in anxiety that is roughly half the distance between the median clinical and non-clinical score on the relevant anxiety measure. In situations when it might be difficult to map effects on to cognitive or behavioral targets, it would be beneficial to compare effect sizes to developmental changes such as annual change in the brain metric of interest for the age range studied.

It is tempting at this point to give some general recommendations of expected effect sizes to plan studies around, the interpretation of such effect sizes, or appropriate sample sizes for adequate power to detect these effects, but it is beyond the scope of this manuscript to make specific recommendations that would apply to the diverse array of work being done in this field. For example, power is a function of sample size, but also number of measurement occasions, and precision (Hansen and Collins, 1994); other considerations, such as representativeness also influence sample size decisions. Decisions about effect sizes similarly require reference to the particulars of the context of research and domain expertise (why an effect size matters for some particular distal outcome of interest, or across a particular developmental period). See Box 2 for tools to aid in power analysis for complex designs.

2.4. Correcting for multiple tests: Thresholding of neuroimaging data

In fMRI analyses, we must correct for multiple comparisons on a large scale—across tens or hundreds of thousands of voxels in standard massive univariate analyses. Researchers correct for multiple comparisons by attempting to control the rate of family-wise error (FWE; i.e., the probability across infinite study repetitions of one or more voxels being identified as a false positive) or the false discovery rate (FDR; the proportion of false discoveries among all discoveries). We focus on FWE given the high prevalence of cluster-based thresholding in DCN that relies on this approach. While Bonferroni correction is one method of controlling the FWE rate, it is too stringent given that voxels are not spatially independent due to both the raw signal and the introduction of spatial smoothing (that is, the true FWE rate is likely below the nominal rate, which leads to lower power). In contrast, an estimate of the spatial smoothing is incorporated in cluster-based thresholding, which includes both a primary cluster-defining voxel-wise p-value threshold and a cluster-extent threshold (i.e., minimum size of cluster in voxels). This method relies on the assumption of random field theory to control the FWE rate by generating expectations about the threshold at which one or more clusters are expected to exceed threshold under the null hypothesis in 5 % of simulated study repetitions. Importantly, cluster-corrected FWE techniques move inference and error control from the level of the voxel to the whole cluster, preventing within-cluster inferences (i.e., we only expect to see a false-positive cluster at the rate determined by our family-wise alpha threshold; Woo et al., 2014).

2.4.1. Arbitrary and parametric cluster-based thresholding

Cluster-based thresholding approaches are quite common in task fMRI studies, including in DCN. However, there are multiple potential issues with cluster-based thresholding, as revealed by Eklund and colleagues (2016). Concerns about poorly controlled FWE in cluster-extent thresholding may be most severe when there are no attempts to obtain true smoothness estimates (e.g., by using the smoothing kernel as the smoothing estimate), or when arbitrary cluster extents (e.g., p <  .005 and 20 voxels) are selected. Many studies have utilized this latter technique over the years, based on prior methodological recommendations (Desmond and Glover, 2002; Lieberman and Cunningham, 2009) and driven by the limited power of early studies in the field (Poldrack et al., 2017). We suggest it is necessary to both (i) critically assess whether confirmatory approaches can adequately address the question at hand given the available data, and (ii) acknowledge when confirmatory approaches may yield ambiguous results.

Some examples of ambiguous findings that track with examples used above are null results in studies that are too underpowered to reject the null hypothesis when it is false, or clusters identified in studies where analytic decisions have been contingent on the data (and the likelihood of false positives has become unknowable). A novel example of ambiguous findings are the extremely large clusters in better-powered studies that lose spatial specificity (an issue described in Woo et al., 2014 and discussed further in section 2.4.3). In such cases, we suggest it is appropriate to supplement with exploratory and comprehensive reporting, and recommend that we abandon arbitrary thresholding approaches used previously in the field.

Another significant problem can be attributed to issues with commonly used software packages (e.g., AFNI 3dClustSim) for estimating cluster-extent thresholds using the parametric assumptions of random field theory. Historically, these programs have relied on the unlikely assumption that underlying spatial autocorrelations in fMRI data take on a Gaussian form. Simulations demonstrate that actual FWE rates obtained from under this assumption are much higher than intended, and that this problem is not modality-specific (see Greve and Fischl, 2018 for an assessment of this issue in structural neuroimaging). For task fMRI, this issue is most problematic at primary cluster-defining thresholds which are as or more liberal than p = 0.005, but simulations suggest that it is possible to approximate a true FWE rate of 5% by using a primary cluster defining threshold which is as or more conservative than p <  .001 (Eklund et al., 2019, 2016).

Box 1: Spotlight on conducting and reporting cluster-based thresholding

Inflated FWE rates have been reported among parametric methods for clusterwise inference in FSL, SPM, and AFNI software packages (Eklund et al., 2016). For FSL users, FLAME1 demonstrated a consistently valid FWE rate. While AFNI’s 3dClustSim did not perform as well, this program underwent additional development and testing. Considering that no comparable updates have emerged from SPM, AFNI programs may be a viable approach for AFNI and SPM users alike. Moving between programs (such as from SPM to AFNI 3dClustSim) has been criticized as a form of “methods shopping” for greater sensitivity (Poldrack et al., 2017); however, updates to AFNI programs provide SPM users with a more accurate FWE rate and a sense of the conditions under which this rate may be inflated. Detailed by Cox and colleagues (Cox et al., 2016), these updates include (a) fixing a software bug in 3dClustSim, (b) assuming a Gaussian plus mono-exponential rather than strictly Gaussian form of the spatial autocorrelation function of noise in fMRI in 3dClustSim (with the use of the -acf flag), and (c) adding a nonparametric test, specifically permutation testing, to 3dttest++.

In order for SPM users to employ parametric approaches in AFNI, they will need to write individual-level residuals from the first-level (single subject) models and apply these to the AFNI function 3dFWHMx to estimate individual-level autocorrelation function parameters (abbreviated as “acf” in AFNI documentation and manuscripts). These estimates can then be averaged across individuals and entered into AFNI’s 3dClustSim to generate tables of cluster-size thresholds for a range of primary p-value thresholds and overall FWE values. For instructions,code, and sample text for a Methods section for this procedure, see https://osf.io/y2nm8/.

Authors should report the software package (including the specific release version) used to calculate thresholds, particularly if it is not integrated within the software program(s) used for other aspects of preprocessing and analysis. As described above, some of these programs, like 3dClustSim, require inputs specific to each first-level model (if multiple such models are made), such as estimated parameters describing the spatial autocorrelation function of the model residuals and the size of the search space. Any such inputs should be reported as well, including how they were calculated. We also suggest providing information about the magnitude (e.g., a t or z value) which would achieve appropriate FWE correction for multiple comparisons on a solely voxel-wise basis, as a reference point. It is also important that the final voxel dimensions (after preprocessing) be reported, since often only the acquisition dimensions of voxels are noted (as part of the scan sequence). For further guidance on other information to be included in methods sections, please see Poldrack et al. (2017) and Wicherts et al. (2016), as well as the user-friendly checklist recently developed based on the recommendations of the Committee on Best Practices in Data Analysis and Sharing (COBIDAS) of the Organization for human brain mapping (Gau et al., 2019).

-- End of Box 1 --

2.4.2. Non-parametric thresholding

A true FWE rate of 5 % can also be achieved via nonparametric methods (Eklund et al., 2016). Compared to parametric clustering methods, non-parametric methods make weaker assumptions about the underlying null distribution of the statistic, and the spatial distributions of signal under the null hypothesis within neuroimaging data, as well as the form of the null distribution of the voxel-level test statistic. In order to do this, non-parametric methods typically use permutation to generate the null distribution from the observed data which provides both the voxel-level permutation p-value, as well as the spatial distribution of these p-values for each permutation (note that the parametric clustering methods addressed above also generate permutations of the spatial distribution under the null using a parametric model of spatial autocorrelation). This delivers robust type 1 error control, as well as potentially higher statistical power, at the cost of additional computational time. However, these methods are uncommonly employed in DCN, despite the relative ease of exploring simple designs using 3dttest++ in AFNI (https://afni.nimh.nih.gov/pub/dist/doc/program_help/3dttest.html), Statistical NonParametric Mapping (SnPM; http://warwick.ac.uk/snpm; Nichols and Holmes, 2002), FSL’s Randomise (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Randomise) and PALM (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/PALM), and BROCCOLI (https://github.com/wanderine/BROCCOLI). While nonparametric methods may currently be too computationally demanding for complex designs, the proliferation of high-performance computing resources available to researchers may eventually eliminate this issue. One piece of software, Neuropointillist, provides a flexible framework that allows researchers to use cluster computing resources for custom, voxel-wise neuroimaging analyses, which could include non-parametric tests specific to complex designs (Madhyastha et al., 2018). Other ostensible barriers to employing these methods in non-experimental designs have been overcome, such as how to handle covariates (Winkler et al., 2014), and how to permute data in nested designs (Winkler et al., 2015). As a first step towards integrating this practice into our arsenal, we encourage increasing familiarity with nonparametric methods by repeating analyses using 3dttest++, SnPM, Randomise, PALM, or BROCCOLI as a kind of “sanity check” (for an example, see Flannery et al., 2017).

2.4.3. Threshold-free clustering

Another set of tools to consider is threshold-free cluster enhancement (TFCE; Smith and Nichols, 2009), its probabilistic variant (pTFCE; Spisák et al., 2019), and equitable thresholding and clustering (ETAC; Cox, 2019), as these methods obviate having to set an arbitrary primary cluster-defining threshold. Both TFCE and ETAC make use of the permutation methods discussed above. Because threshold-free techniques take into account both the cluster’s signal amplitude and extent, these methods are more sensitive than cluster-based thresholding. For example, clusters of high amplitude but small extent would typically not survive in traditional cluster-based thresholding; this may have a pronounced impact on small anatomically defined structures (e.g., the nucleus accumbens or amygdala). Software that can be used to implement TFCE with fMRI data is available in FLS’s Randomise (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/Randomise; Winkler et al., 2014), and at https://github.com/markallenthornton/MatlabTFCE; pTFCE implementation for multiple platforms can be found at https://spisakt.github.io/pTFCE/; and ETAC is implemented in AFNI’s 3dttest++ and 3dXClustSim).

2.4.4. Thresholding robust effects

The steady increase in average sample size of DCN studies, and emergence of large research consortia (e.g. IMAGEN, ABCD, HCP-D, and Lifebrain) reveals a problem researchers would likely have envied over a decade ago. Namely, main effects for many canonical fMRI tasks are extremely robust, such that the cluster thresholding procedures described above produce only a small number of clusters with tens of thousands of voxels in them (“supraclusters”). We have observed this in our own work as sample sizes approach merely 100 participants. Supraclusters can sometimes also arise in studies that are not as well-powered, when one uses a cluster threshold with a more relaxed magnitude statistic (and therefore much larger extent) to still achieve FWE correction of p <  .05. These findings are difficult to interpret because one cannot make inferences about the multiple anatomical regions spanned in these supraclusters, as described fully by Woo and colleagues (2014). If one increases the stringency of correction by decreasing voxel-wise alpha or cluster-forming p-value, other analyses that may be less well-powered (such as individual differences in brain-behavior associations) may produce few or no clusters at the same thresholds.

One approach to consider is using different voxel-wise FWE rates, or cluster-forming thresholds, across analyses within a study (note that this does not include using an arbitrary threshold, which is problematic for the reasons described above in section 2.4.1). For example, running power analyses for group-level main effects may help identify when even more stringent thresholding (i.e., a lower alpha level, and/or a smaller cluster-forming p-value) may be warranted, thus allowing us to make more precise inferences about extremely well-powered effects. Alternatively, thresholding based on effect sizes of interest may also help decipher practically meaningful effects in such instances, although until the neuroimaging research community more commonly reports effect sizes, this may be difficult. It also bears repeating that this phenomenon of supraclusters with large spatial extent also illustrates the limitations of using the absence of a significant p-value in some cluster to infer it is not involved in a task (see section 2.3), and that better-powered studies reveal that more of the brain is involved in mental processes than we previously realized. In general, our most basic suggestion is that researchers make transparent, a priori decisions about thresholds that both (i) control type 1 error at a known level, and (ii) identify meaningful and interpretable results.

2.5. Computational modeling and specificity

Another possible route toward improving inferences and replicability in confirmatory research is to enhance the value of data as evidence by increasing the degree of specificity of our theories, and ultimately encoding them as computational models that describe mathematical relationships between constructs. Currently, much work in DCN is guided by broad, heuristic theories that generate many possible hypotheses (Pfeifer and Allen, 2016). We test these by asking whether we can reject a proposition that is not consistent with our theory (usually the null hypothesis that some parameter is exactly equal to zero), and if we can, take this as evidence that our observations are consistent with our theory, which is sometimes called verification (Eysenck, 1997) or corroboration (Meehl, 1990). Corroboration via null-hypothesis rejection does not constitute a severe test of the hypothesis (i.e., a test that is likely to fail just in the case that the hypothesis is wrong; Mayo, 2018) because we rarely take a failure to reject the null as evidence against the alternative hypothesis or generating theory (even in well powered studies). Such a null result (i.e., failure to reject the null) does not usually impinge our hypothesis because the theory is not so specific that it can rule out the possibility that, for example, unknown boundary conditions and context effects lead to occasional failures of our broadly specified hypotheses. Indeed, often our theories do not lead us to specify a null hypothesis that, if not rejected, would actually put our theory in jeopardy. In other words, we often specify a null of absolutely no effect which leaves open the possibility of accepting very trivial effects as evidence for our hypotheses and theories (or even ambiguous effects, such as when one’s target brain region shows an effect, but others, unspecified by the theory, also show effects, sometimes larger than in the target region). In many cases, researchers might describe this as a process of discovery through which theories are refined, but this strategy can easily lead to a “degenerate” research program in which each failure becomes attached to a long list of caveats that reduces the theory’s generality or, perhaps worse, where these failures are marginalized as merely very narrow theoretical limitations (see Meehl, 1990 for in depth discussion of this application of Imre Lakatos’ philosophy of science).

Oberauer and Lewandowsky (2019) describe this state of affairs, when hypothesis tests are able to corroborate but not falsify theories, as characteristic of a research program that is discovery oriented, which is at one end of a continuum; at the other end is theory-testing, which requires that we develop theories that can deductively generate specific hypotheses that almost certainly have to be true if our theory is true. Such hypotheses, if not supported, have strong evidentiary value against the theory. While replication and stringent statistical testing, perhaps including preregistration, is necessary for building up evidence for theories in a discovery oriented program, these authors suggest that very specific theories reduce the need for preregistration because they eliminate ambiguity about what tests would be consistent or inconsistent with a theory, and thus greatly constrain the universe of forking paths.

In order to move toward theory-testing, the first step is to increase specificity along the many dimensions that currently characterize our field. We have previously recommended a checklist (Pfeifer and Allen, 2016) which, if followed, would increase specificity at multiple levels from theory, to construct definition, to translational significance. Each additional degree of specificity enhances the value of corroborative findings for discovery-oriented research and, by making a theory bolder, moves it toward the theory-testing end of the continuum. As reviewed by Pfeifer and Allen (2016), many of the theoretical frameworks in DCN are formulated in natural language (i.e., colloquial terminology as opposed to mathematical modelling) using heuristic definitions of neural regions and their proposed involvement in cognitive processes and behaviors. Although this degree of nonspecificity may have been appropriate for the state of the field in the past, we can now capitalize on the wealth of knowledge we have collectively accumulated to evolve our theories such that they have greater specificity.

As an example, imagine a student wishes to test a version of social reorientation theory (Nelson et al., 2016) that has been more highly specified. Starting from the theory as written, the student hypothesizes that the salience of social information should gradually increase from childhood through adolescence, and then decline into adulthood; moreover, this should be reflected by a similar trend in neural activity in the ventromedial prefrontal cortex (vmPFC). The student then uses existing research on social reorientation, and other relevant theory and empirical work, to make their predictions more specific by detailing the types of social information (e.g., peer- versus parent-relevant); specifying relevant, functionally distinct sub-regions of the vmPFC (either through meta-analysis or localizers; Delgado et al., 2016); or proposing the functional form of the trajectory and age of expected “peaks”. The experimental design would reflect this specificity by ensuring valid operationalization and measurement of the construct “peer-relevant social information”, robust measurement from the target brain region, and targeted sampling of the relevant age range appropriate to the developmental trend(s) being tested. The treatment of adolescence could be further enhanced by specifying biological and social markers of development, rather than using chronological age as a proxy. Doing so would demand additional refinement of the mechanisms thought to underlie social reorientation as a biopsychosocial process. Finally, the translational significance would be enhanced to the extent the theory can specify its applications in the public interest. In this example, if the theory implies that social reorientation increases sensitivity to peer influence, the specific translational relevance could be assessed through observation of that real-world outcome of interest.

A theory that survives such commitments to specificity may be considered to have survived severe tests commensurate with the level of risk implied by that degree of specificity (Mayo, 2018). This clearly requires a theory to be considered in jeopardy if its specific predictions are not borne out; importantly, it is not sufficient for inconsistent evidence to be incorporated as a sort of post-hoc singular exception, boundary condition, or context effect (especially when such results accrue; Meehl, 1990). As it stands, social reorientation, like many of our most well-developed theories, does not yet commit to even the more vaguely specified prediction regarding the vmPFC described in the above example. This may be appropriate—this theory, and the field generally, seems to be very much in the discovery phase, and committing to too-specific predictions could lead us to discard a useful heuristic that will bring us closer to a more robust theory. However, it behooves us to be aware of how specificity indicates the position of a theory on this continuum from discovery to theory testing, to work to move it toward the theory-testing pole, and to guard against excessive post hoc auxiliaries to the theory.

Finally, an optimal way to reap the evidentiary benefits of specificity is by instantiating theories as formal or computational models that allow theory-testing (Oberauer and Lewandowsky, 2019). This is not a simple endeavor, but one that has an important role to play in developmental science (Simmering et al., 2010), and can be pursued with the aid of understanding how such models might be created. For an in-depth overview of computational modeling in psychology, see Farrell and Lewandowsky (2018); for overview of mathematical models of the evolution of sensitive periods, see Frankenhuis and Walasek (2020); for a foundational example in vision, see Marr (2000); and for a method of building mechanistic models using functional analysis, see Piccinini and Craver (2011). It is important to note that computational models are not immune from ambiguity, so care must be taken to challenge the model, for example, by ensuring one’s model can not equally well describe data generated from alternative data generating processes, or that alternative models do not equally well describe the target phenomenon. However, the process of instantiating a theory as a computational model requires, much like preregistration, attention to underexamined implications and prerequisites that will often enhance specificity.

3. Exploratory analyses

There are many reasons a researcher would want to go beyond testing a priori hypotheses, and explore their data in ways that can lead to broad understanding and generate novel hypotheses. Especially in the field of DCN where current theory is based on a relatively short history of observation, it is necessary to build up a broad descriptive base of effect size estimates and model explorations that will allow for theory construction. Principled exploratory procedures are crucial for making use of data that is difficult and time consuming to collect for both the researcher and participants. Low power in many non-consortia based neuroimaging studies (Poldrack et al., 2017), as well as fairly young and sparse theoretical bases for generating a priori hypotheses, may lead to a higher rate of low-information null findings in DCN than in other fields. When planned confirmatory hypothesis tests reveal null findings, researchers wanting to avoid running alternative hypothesis tests or changing their analysis plan may feel they are left with nothing to publish.

In all of the above cases, it is important to remember that there is still much to be gained from our hard-earned datasets if we adjust our perspective away from NHST. Indeed, this reframe is recommended rather than trying to force conventional statistical significance in a confirmatory framework. In the following section, we describe tools that make the best use of these data. We begin by reviewing several approaches for describing and interpreting data that do not require specific hypotheses to be determined prior to seeing the data. We then discuss ways that make presentation and interpretation of these statistics easier in DCN research. Before continuing, it is important to note that, as with any analytic method, it is possible to selectively report non-NHST exploratory results. Pre-specification (or otherwise transparent reporting) of structured, systematic exploratory strategies will enhance the strength of these contributions as well. We take up the discussion of that issue in section 4.

3.1. Focus on estimation

We suggest considering the maps resulting from group-level analyses just like any other set of variables for which one would report descriptive statistics. Typical reporting methods would include something like a group mean and standard deviation for each voxel, for each condition, for each group. Given recent evidence of somewhat poor reliability of task-fMRI measures (Elliott et al., 2020), it would also be extremely informative to report comprehensive measurement characteristics (e.g., internal reliability, test-retest reliability, or intraclass correlations; for a developmental example, see Herting et al., 2018; a comprehensive toolbox is provided by Fröhner et al., 2019). Though in the past this kind of reporting would have been difficult or impossible (printing a table with tens of thousands of rows is obviously impractical), tools like NeuroVault (https://neurovault.org/) and OpenNeuro (https://openneuro.org/) have made it trivially easy. For example, unthresholded maps for any of the commonly generated statistics (i.e., t, F, beta, percent signal change, contrast) can be uploaded to NeuroVault for examination in 3-dimensional space. Uploading effect size estimates, specifically either statistical parameter maps of standardized regression coefficients (“beta maps”) or unstandardized BOLD signal contrast maps, to NeuroVault also allows for future re-examination of results using a confirmatory meta-analytic approach. Integration of results across multiple studies on NeuroVault increases the power to detect true effects with good FWE control, and also supports future power calculations.

Certain data visualization and sharing practices can more completely convey descriptive, exploratory results of a study. For example, one may add more layers to the image, or change the transparency of the effect colors to represent multiple dimensions of the data (Allen et al., 2012). While it might be tempting to take this approach using statistical maps thresholded by p-values, we recommend that exploratory studies do so using effect sizes, with any standardization clearly described.

A clearly scaled map of standardized effect sizes is perhaps the easiest to interpret both within and across studies. As fMRI data are often reported using non-meaningful units and different software packages calculate different effects (e.g., mean differences, percent signal change), standardization aids comparison of effect sizes across studies. This is preferable to a qualitative approach that focuses on “vote-counting” (tallying the number of studies that find an effect against those that do not; Pfeifer and Allen, 2016), which confounds effect size and power. Standardizing effect sizes can be done many ways (see Lakens, 2013 for a practical primer on calculating effect sizes). For clarity of interpretation, the method used should be clearly stated and tied to the relevant exploratory question. Note that for the goal of comparing across studies we recommend reporting standardized effect sizes, though above we recommended a different approach for more concrete interpretations.

3.2. Parcellations

The use of parcellations may facilitate exploratory work. Parcellations divide the brain into non-overlapping regions that share certain structural and/or functional properties. They help reduce mass univariate data to a smaller number of parcels or regions that can be more easily explored and presented in manuscripts. Parcellations provide an unrestricted search space while supporting exploratory strategies, by producing a more manageable number of features for input to analyses (e.g., nodes for graph-theoretical approaches) as well as outputs for interpretation (e.g., developmental trajectories for each parcel). They facilitate the comprehensive reporting of effect sizes (and possibly other statistics of interest) in both confirmatory and exploratory research without the biasing effect of selecting regions based on significant p-values (Chen et al., 2017). Many parcellation schemes also group parcels into networks, adding another layer of data reduction to ease interpretation. In short, they represent a principled way to select sets of regions of interest that are both easily specified a priori and facilitate reproducibility when there is not an adequate literature to pursue confirmatory analyses for fewer, or even singular, regions of interest.

Quite often, parcellation approaches have been used to divide the brain into structurally-defined regions (e.g., FreeSurfer; Harvard-Oxford atlas); however, it is becoming increasingly common to apply a parcellation approach to fMRI data using connectivity-based parcellation (CBP) techniques (Craddock et al., 2012; Eickhoff et al., 2015; Gordon et al., 2016; Schaefer et al., 2018; see Eickhoff et al., 2018 for a broad overview). While structurally-defined parcellations are based on landmarks or cytoarchitecture of the cortex, CBP methods are defined by signal homogeneity across voxel timecourses, typically during resting-state scans in which participants remain in the scanner with minimal stimuli. Multi-modal parcellations incorporate multiple types of neuroimaging data, and are quite a bit less common (Glasser et al., 2016; Ji et al., 2019). Complicating the picture further, there is some evidence that stable parcellation schemes differ from participant to participant in a way that can be captured by recently-developed machine-learning methods (Abraham et al., 2013; Varoquaux et al., 2011), but also that these maps might differ even between different psychological states (Salehi et al., 2018). Ultimately, it is unlikely that there is any one optimal parcellation scheme and so the choice must be made based on the researcher’s questions and goals (and done so transparently, e.g., via preregistraion).

One potential limitation is that most approaches to parcellation thus far have been based on adult samples. Recent work suggests that the topography of functional networks is refined across childhood and adolescence (Cui et al., 2020), and it is unclear how well current (adult-based) parcellation schemes apply to developmental populations. However, this could be potentially overcome by generating parcellations specific to individuals (Glasser et al., 2016). Another issue is the granularity of the parcellations. Too few parcels in a given set averages activity across large regions, which may make spatial interpretation challenging, but too many parcels make visualizing and synthesizing the results difficult. Finally, after identifying a parcellation approach to use (a robust list of existing parcellations is provided by Eickhoff et al., 2018), one must decide how to apply the parcellation. The parcellation can be applied to group-level, individual-level, or even trial-level maps.

A multi-level Bayesian approach can make use of parcellated data by pooling information across the whole brain and providing effect size estimates that are more precise than they would be were a model estimated separately for each ROI. AFNI provides a tool, called RBA (“Region-Based Analysis)”, to analyze data extracted from ROIs or parcellation schemes using this approach (Chen et al., 2019). ROIs, as well as participants, are used as grouping factors in a hierarchical linear model; thus fixed effects (at the population level) are estimated across participants and ROIs, and effect sizes (often called random effects) are estimated for each ROI. In the context of Bayesian analysis, the partial pooling and resulting estimate “shrinkage” toward the fixed effect mean produces probability densities that can be interpreted as straightforward estimates of effect sizes that are already adjusted for the multiplicity of effects (Gelman et al., 2012). The RBA tool makes this method easily accessible for a subset of models, but the general approach is extremely flexible.

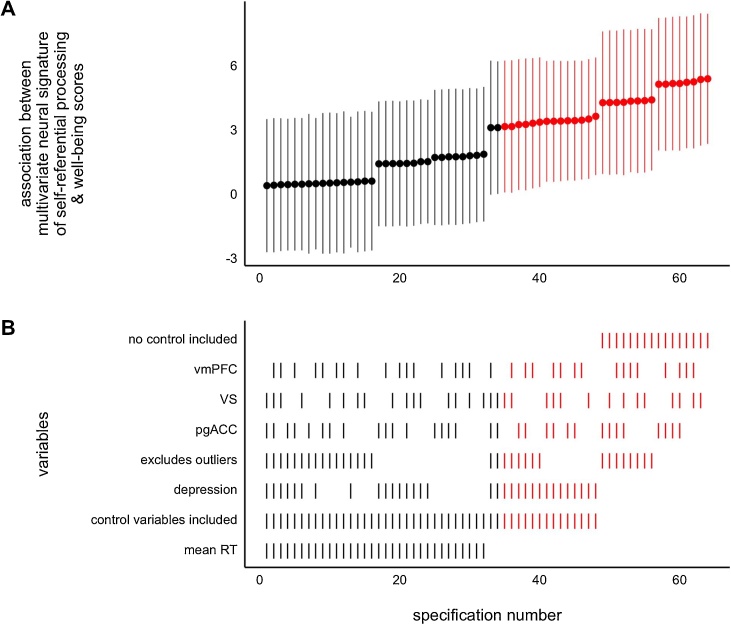
3.3. Specification curve analysis in neuroimaging

Specification curve analysis is a versatile method that can be used both in confirmatory (e.g., Orben and Przybylski, 2019a,b, Cosme & Lopez, preprint) and exploratory (e.g., Cosme et al., 2019) contexts to quantify and visualize the stability of observed effects across many possible models (i.e., specifications). The specification curve framework (Simonsohn et al., 2015; Steegen et al., 2016) was developed as a solution to the problem that there are myriad ways to test an association between variables, but we typically only report one or a few model specifications. These reported specifications are the product of choices made by researchers, which are often arbitrary and are susceptible to pressure to produce significant results. To account for this, Simonsohn et al. (2015) suggest estimating (specifying) all “reasonable” models that test a given association in order to assess the effects of analytic decisions. For each decision point, researchers specify alternative decisions that could have been made. For example, researchers might have used a 6 mm smoothing kernel, but could have chosen 4 mm or 8 mm. Or they may have chosen to exclude several participants based on a motion artifact threshold of 10 % of volumes, but it could have been specified at 15 % or 20 % instead (for such an exploration, see Leonard et al., 2017). Reasonable model specifications are defined as being: consistent with theory, statistically valid, and non-redundant (Simonsohn et al., 2015).

Once all reasonable models have been run, results from each model specification are ordered based on effect size and plotted, generating a curve of model specifications (Fig. 1A). Typical specification curves also include graphical information detailing which variables or analytic decisions were included in each model (Fig. 1B). This can reveal patterns in the data regarding how specific decisions impact effect size estimates, which might not have otherwise been apparent. In addition to testing the effect of methodological decisions, such as smoothing kernels or exclusion thresholds, specification curves can be used to visualize the effects of including (or not including) potential covariates, such as age, pubertal status, sex, or other individual difference measures. Researchers can choose to visualize the effect of these covariates or analytic decisions on a specific relationship (e.g., the parameter estimate for the effect of age on BOLD signal in vmPFC) or to compare model fit indices as a function of analytic decisions and/or covariates. This method is extremely flexible and can be used in nearly any situation in which there are multiple potential model specifications.

Fig. 1.

Sample specification curve analysis of 64 unique linear regression models with individual well-being scores as the criterion. Model specifications are ordered based on the parameter estimate for the association between individual whole-brain pattern expression of a multivariate neural signature of self-referential processing and well-being scores. Each vertical column corresponds to a single model specification. The regression coefficient for each model specification is plotted in panel A and the variables included in each model are visualized in panel B. Models in which the association between multivariate expression and well-being score is statistically significant at p <  .05 are highlighted in red. Error bars represent 95 % confidence intervals. Control variables included depression scores and mean reaction time. Outliers were defined as being more than 2.5 standard deviations from the mean for each variable. pgACC = perigenual anterior cingulate cortex, vmPFC = ventromedial prefrontal cortex, VS = ventral striatum. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).

As mentioned above, in constructing specification curves, only reasonable specifications should be included to reduce the extent to which problematic specifications bias the ultimate interpretation. For example, with respect to inclusion of different permutations of covariates, it may be the case that at least some of the specifications encode problematic causal relations that should be discounted a priori because they introduce known or suspected bias either because confounders are not accounted for or collider variables are erroneously included (Rohrer, 2018; Westreich and Greenland, 2013). Researchers can attempt to avoid these problematic specifications by analyzing plausible causal structures through the use of graphical causal models (e.g., using packages such as ggdag and dagitty; Barrett, 2020; Textor and der Zander, 2016). Measurement (in)validity, with regard to questionnaires, tasks, or even how the BOLD signal is modeled, may also contribute to erroneous specifications, and is another domain that should be carefully attended to when determining specifications (Fried and Flake, 2018). The possibility of bias of the mean or median effect in a specification curve due to incorrect specifications reveals another challenge to interpretation. It is likely that a particular specification is, in fact, the closest to the (unknown) true model, and thus provides the least-biased estimate of the effect of interest. This estimate may or may not be close to the central tendency of the curve as a whole, and so interpretation should be guided in part by this possibility. The choice of the final set of reasonable specifications will depend on the judgement of the researcher and their domain expertise, as well as expertise in statistical modeling, with arguments made on the basis of the patterns that are common across all specifications. This clearly increases the burden to defend the entire set of specifications as reasonable, but this is likely appropriate for domains where such an exploratory strategy is necessary (that is, where the data generating process is not well known).

To implement a specification curve analysis, researchers must first summarize the MRI data in some fashion, guided by the research question. For questions about specific regions, researchers might parcellate the brain, select reproducible ROIs, and extract parameter estimates for each individual. For questions regarding whole-brain pattern expression, they might multiply individual maps with a meta-analytic map to assess individual expression of a multivariate pattern (Cosme et al., 2019). Once the data has been summarized, a series of reasonable models are specified and run (for a tutorial using R, see Cosme, 2019), and plotted based on parameter estimates of interest or model fit indices. The specification curve can assess the robustness of an effect to various analytic decisions or inclusion of covariates, as well as whether effects tend to be positive, negative, or zero.

While visualization alone may be useful in exploratory analyses to identify stable (or unstable) effects, and potentially generate novel hypotheses based on patterns in the data, specification curves can also be used in confirmatory analyses to compare a given curve to a null distribution curve using permutation testing (Simonsohn et al., 2015), though this is challenging for some of the more complex designs in DCN research. In this context, researchers might compare the median effect of an observed curve to the median effect from a curve from a null distribution; or they might compare median effects between two curves of interest (e.g. curves for the effect of age vs. pubertal status on vmPFC activity, or effect of vmPFC vs. NAcc activity on sensation seeking). Alternatively, they might be interested in comparing the proportion of positive, negative, or statistically significant effects in an observed curve to the proportion in a null curve (Cosme & Lopez, preprint). This approach can be particularly powerful when researchers have a priori hypotheses suitable for confirmatory analyses, but face a number of decision points that may influence the results. It also has the potential to help identify which statistical effects are robust and relatively stable across specifications, and which effects are largely dependent on specific choices or inclusion of specific variables. In the long run, this information can help direct research programs toward the study of robust developmental effects.

4. Transparency and reproducibility

Many of the concerns discussed above can be addressed through detailed analysis plans and comprehensive reporting of methods and results. Such practices improve transparency, reproducibility, and ultimately scientific knowledge derived from both confirmatory, and exploratory research.

4.1. Detailed analysis plans

Preregistration and Registered Reports are two options for providing detailed analysis plans, and are valuable solutions to protect against the threats to confirmatory analyses described in section 2. Creating detailed analysis plans helps to reveal procedural or theoretical gaps, such as lack of knowledge about how to analyze data from a new method, or insufficient evidence base or ambiguous theory which precludes precise hypotheses. To the extent that many unknowns are identified and hinder creation of a detailed analysis plan, it suggests one is conducting truly exploratory work and may benefit from alternative approaches to NHST. Researchers may also preregister a combination of confirmatory and exploratory aims with appropriate justification, which might mitigate concerns during the peer review process as to why NHST was not undertaken. Though the following focuses on confirmatory NHST, exploratory analyses may also benefit from pre-specification of analysis plans to minimize the possibility of selective reporting and file drawer effects.

4.1.1. Preregistration

Preregistrations may be submitted at various points in the research process, and may be an optimal starting point for researchers to increase their comfort with open science approaches. Using the Open Science Framework (OSF), for instance, preregistrations can be embargoed and updated over time (for a comprehensive introduction to preregistration, see https://cos.io/prereg/). Publicly registering standard operating procedures, which define common default practices in a lab such as preprocessing decisions (Lin and Green, 2016; Srivastava, 2018), can also simplify the preregistration of subsequent analysis plans. Preregistration of analysis plans may also promote collaboration across labs, as it lends itself towards sharing of tasks and protocols, thereby promoting reproducibility and meta-analyses. In addition to supporting the integrity of research findings, preregistration facilitates a more straightforward analysis, writing, and review process, and in some cases promotes project dissemination and collaboration.

4.1.2. Registered reports

While it remains an option to keep preregistration private until the manuscript is ready for publication, an alternative approach is to pursue a Registered Report journal article (see https://cos.io/rr/; Chambers, 2013; Hardwicke and Ioannidis, 2018) and get feedback from peers prior to conducting the study (collecting and/or analyzing the data), thus providing a vetted protocol and a conditional guarantee of publication (known as an In-Principle Acceptance). Registered Reports provide the highest level of confidence about the exact number of decisions made and hypothesis tests run, as they are submitted in advance of data analysis (or in some cases, data collection) and vetted by the peer review process. We are thrilled that this article type is now available at Developmental Cognitive Neuroscience (for more details, see Pfeifer & Weston, 2020), and that Registered Reports proposing secondary data analysis are fully welcomed by DCN (for a discussion of the strengths of secondary data analysis, see Weston et al., 2019).

Box 2: Making preregistration practical.

The practice of preregistering detailed analysis plans (including submitting these for peer review via the Registered Reports process) is still relatively infrequent within DCN research. Some of the reasons that have made disciplines with complex methodology hesitant to adopt preregistration of detailed analysis plans are also some of the best arguments for doing so. Complex, multi-stepped methodologies produce problematic levels of analytic flexibility, and dramatically increase the likelihood of inadvertently limiting future replicability and reproducibility.

In this box, we list a series of potential obstacles we and others have encountered in the process of producing detailed analysis plans, as well as approaches that have worked for us. These examples are oriented around preregistration; however, much of the content is applicable to Registered Reports. Furthermore, we note that both preregistration and Registered Reports are part of a rapidly evolving area of open science for which the “gold standard” is likely to evolve, as these practices become the norm (Nosek and Lindsay, 2018).

Unsure how to start. Templates or step-by-step guides help ease researchers into how to create a detailed analysis plan. There have been recent efforts to adopt the standard preregistration template for specific approaches such as secondary data analysis (https://osf.io/x4gzt/) and fMRI studies (https://osf.io/6juft/). We also encourage readers to check out a recent comprehensive crowd-sourced resource for preregistration of fMRI studies (https://docs.google.com/document/d/1YrBc_bFlnWJVSjLjqQ_rRKtRMh9TTLLUcYMCsORg7Y0/edit), which includes a link to a sample fMRI preregistration (https://osf.io/5mx3 w).

Protracted time course of studies. Meeting the ideal of preregistering analyses prior to data collection is challenging in DCN research. The time course for our projects (from initiation to completion) can be several years, and even longer for longitudinal studies. Neuroimaging methods and standards may evolve considerably over this period, making it possible for preregistrations to become outdated by the end of data collection. Despite these challenges, the benefits of preregistration can still be reaped by striving for the highest level of transparency, even after data collection has begun or been completed. The OSF motto is that a preregistration is “a plan, not a prison” (for a counterpoint, see Devezer et al., 2020) As new methodological or practical considerations come to light, preregistrations can be amended by creating a (time-stamped) addendum that is linked to the original preregistration (under the same OSF repository with an updated version number), which justifies modifications to the original analysis plan (e.g., “thresholding criteria was updated to use a new approach based on recent paper, and this was done prior to data analysis”).

Complexity of collaborations. Given the scope of many DCN studies, it is common for many papers to be published from a larger parent project. This raises the question, how much information about the larger study should a preregistration include? One way to deal with this is to make a larger project on OSF, and for all preregistrations to be linked under this umbrella project. Another alternative is to write a study protocol, which can be published on preprint servers (or in some journals, particularly if the protocol is submitted before any other papers from the project have been produced; for example, see Barendse et al., 2019). Preregistrations should also be fully transparent by including a section that describes the author’s prior knowledge of the dataset, including links when possible (e.g., to poster or talk presentations). This section might state how prior information influences (or will be prevented from influencing) the preregistered hypotheses.

Conveying a vast number of decisions. Standard preregistration templates do not currently prompt authors to explicitly specify decisions occuring along the neuroimaging pipeline from study design, MRI acquisition, preprocessing pipelines, ROI definitions, or individual and group level modeling parameters. One solution is to use the Brain Imaging Data Structure (BIDS) & associated BIDS Apps (https://bids-apps.neuroimaging.io/) which allow researchers to concisely share exact analysis pipelines, with the specific software and versions. Many labs also have standard operating procedures and pipelines that can be referenced or linked in preregistrations. Even with the best templates and guides in hand, one must be aware of MRI reporting standards to identify what needs to be included in detailed analysis plans. In 2016, the Organization for Human Brain Mapping completed its Committee on Best Practice in Data Analysis and Sharing (COBIDAS) report (http://www.humanbrainmapping.org/COBIDAS), which was then updated at a 2019 hackathon to make the COBIDAS checklist easier to use (https://osf.io/anvqy/; Gau et al., 2019). A practical guide for improving transparency and reproducibility in neuroimaging research focusing on reporting standards is also available (Gorgolewski and Poldrack, 2016), although future readers are encouraged to check the literature for the most recent summaries of reporting standards.

Difficult power calculations. Preregistrations ideally include a justified sample size based on a priori power analyses. However, accurately planning and justifying sample sizes can be less intuitive for MRI studies, particularly longitudinal ones. Common power calculation tools (e.g., G-Power) may not be appropriate for MRI studies, and simulations are much harder with complex study designs. However, there are tools specifically tackling these challenges that would be useful for some neuroimaging preregistrations, such as NeuroPowerTools (http://neuropowertools.org/) or fMRIpower (http://fmripower.org/).

4.2. Comprehensive reporting and meta-analyses

Increased transparency and reproducibility, aided by detailed analysis plans as described above and comprehensive accessible reporting to be described below, will ultimately enable us to conduct meta-analyses and obtain unbiased estimates of the strength of a given effect. Specifically, when results from preregistered analyses are shared without filtering based on the significance of the results, meta-analysis is able to synthesize many, possibly null, findings and produce much more precise and unbiased results. Unfortunately, without full transparency and pre-specification, meta-analysis will continue to be biased by the same factors that negatively affect individual studies, which has led some to argue that, at least for the moment, meta-analysis should be avoided (Inzlicht et al., 2015; Van Elk et al., 2015). Methodological transparency is also especially important to ensure that when studies are included in meta-analyses, potentially relevant study design differences can be appropriately accounted for. However, the incentive to present novel findings often hinders meta-analyses, as true replication studies are rare in DCN, and null findings may often end up in the file drawer. Greater emphasis on reproducibility will thus support this important process in confirmatory science and hopefully reduce current publication bias.

4.2.1. NeuroVault

Scientific transparency includes comprehensive reporting of methods and results. Today, it is still common to create images that highlight the results of interest in a study, but this occludes the effects not visible on a selected slice or surface, as well as obfuscates those that do not survive thresholding (as discussed above in section 2.3). NeuroVault (http://NeuroVault.org/) is a website “where researchers can publicly store and share unthresholded statistical maps, parcellations, and atlases produced by MRI and PET studies” (Gorgolewski et al., 2015). By uploading to NeuroVault, researchers can present comprehensive results of an fMRI study, which may one day replace the need for large, often clunky, tables in papers. Furthermore, presentation of results in this 3D manner overcomes limitations from labeling schemes or the degree of labeling specificity provided within a manuscript, thus enabling readers to more clearly understand the location and extent of findings. We are pleased to see that uploading to NeuroVault is becoming increasingly common in DCN research; in fact, there is now a developmental community on NeuroVault (https://neurovault.org/communities/developmental/), which can allow for additional filtering of literature.

4.2.2. Meta-analysis

In neuroimaging, there are multiple types of meta-analytic procedures. Among the most commonly used are coordinate-based techniques, such as activation likelihood estimation (ALE) and multilevel kernel density analysis (MKDA), which only require the reported coordinates and sample size of studies. However, these methods can be difficult to undertake when studies do not report the coordinates of relevant tests for the meta-analysis (e.g., studies investigating group differences in grey matter volume or density that neglect to report main effects within each group). In addition to reporting main effects to support coordinate-based analyses, regular use of NeuroVault to share whole-brain statistical maps would also enable us to engage in more sophisticated and powerful meta-analytic techniques, such as image-based meta-analysis (which can even be run directly within NeuroVault). These techniques are not limited by methods of defining ROIs or thresholding and reporting data, and can thus pick up on subthreshold effects that are consistently present across studies (Salimi-Khorshidi et al., 2009). If sharing group-level statistics through NeuroVault is for some reason impractical or not feasible for a particular study, there are some reporting practices that can still aid meta-analyses. Given that DCN studies routinely investigate interaction effects (such as differences between age groups in BOLD signal elicited by two contrasting task conditions), researchers should report all simple effects and main effects, not just the interaction effect. These simple and/or main effects may usefully demonstrate replication of past findings, and are necessary for many meta-analytic approaches.

Publication of null results is a crucial aspect of comprehensive reporting that will lead to a less-biased literature which is necessary for accurate meta-analysis. Neuroimaging research that yields no significant results related to the neurophysiological data may be difficult to publish even if the methodology is otherwise sound. Given that these investigations are replications of a particular study design, it is crucial that they be made openly available in order to facilitate future mega-analyses, in which many data-sets produced by similar study designs are analyzed in combination to produce very well powered results (Costafreda, 2009; Salimi-Khorshidi et al., 2009). Such a mega-analysis will yield biased results if it does not include data that is not available just because it did not yield a significant result. Although such data may be uploaded to a repository like openneuro.org, it benefits the researcher and the community to publish a citable data paper with comprehensive details on the protocol and what is available in the data set (Chavan and Penev, 2011; Gorgolewski et al., 2013; for an example data paper, see Botvinik-Nezer et al., 2019).

4.3. Considerations by study size

Smaller studies in DCN (e.g., Ns < 50 per group) remain valuable for a number of reasons. They are vital for hypothesis generation, as well as driving new research directions, including the creation of novel paradigms for use in functional neuroimaging. Many institutions still make hiring and tenure or promotion decisions based on publications that derive from data collected in a single laboratory. Small studies also provide important training opportunities for early career researchers. They may be particularly well-suited to develop familiarity with preregistration of detailed analysis plans, as small studies are more likely to have a limited set of hypotheses and/or measures. The figurative elephant in the room is that larger sample sizes (e.g., Ns ranging from 100 to the 1000s) are becoming increasingly common, and the field is still learning how to appropriately evaluate smaller studies given this expansion of scope. While these standards evolve, utilizing the open science tools discussed in this paper to maximize transparency and reproducibility may mitigate reviewer concerns regarding confirmatory analyses in relatively small studies. We also urge reviewers to calibrate their evaluations appropriately based on the presence (or absence) of preregistration in ostensibly confirmatory papers, and be willing to accept papers with null results that can demonstrate evidence of preregistration and sufficient power to detect meaningful effects. Journals might also consider accepting data papers for small, well executed studies that are not by themselves well-powered enough to deliver strong conclusions.

Although the shift to using larger samples will benefit the field by increasing the power to detect smaller effect sizes in confirmatory analyses, certain characteristics of large studies also warrant special consideration to avoid conflating confirmatory and exploratory analyses. Studies with large samples often collect many more measures on participants, and it is likely not feasible to report all measures collected in each manuscript. Of course, smaller studies collecting deep data from neuroimaging (e.g., precision functional mapping; https://www.openfmri.org/dataset/ds000224/; Gordon et al., 2017) or other sources also face this problem, making a protocol paper useful for these types of projects as well. One useful step for such studies may be to publish a protocol paper that outlines all measures collected in the study (e.g., Barendse et al., 2019; Mundy et al., 2013; Simmons et al., 2014); the ABCD study effectively published an entire issue in Developmental Cognitive Neuroscience detailing the protocol (see https://www.sciencedirect.com/journal/developmental-cognitive-neuroscience/vol/32/suppl/C for a link to the virtual collection). Protocol papers can provide a helpful, broader context for readers in terms of measures reported in a given manuscript versus the larger set that was acquired. Finally, in addition to the recommendations made throughout this paper, interested readers can see Srivastava (2018) for more exploration of maintaining “decision independence” in complicated designs such as those inherent to large multi-site consortia. One possibility that is complex but may be worthwhile to consider for projects with many potential stakeholders (such as large multi-site consortia) is coordinated data analysis. This is a method in which current and future users collaborate to make data-independent analytic decisions.

5. Conclusion

In this manuscript we hope to have increased readers’ familiarity with various research practices that will improve inferences in developmental cognitive neuroscience. Our goal was not to produce a false either/or stance towards confirmatory and exploratory work, or to give the impression that confirmatory analyses are only for large studies and exploratory analyses are only for small studies. Instead, our aim was to foster both an emphasis on enhanced rigor in confirmatory analyses, and enhanced esteem for exploratory approaches. For the field to continue producing the most rigorous science possible, it will be essential to also align incentives in a way that better rewards rigorous confirmatory research, and equally encourages systematic exploratory analysis (and the clear identification of it as such). Key insights for confirmatory research included the tremendous value of creating detailed analysis plans to limit the number of decisions and hypothesis tests to control type 1 error, reminders to avoid incorrect inferences about non-significant p-values or post-hoc simple effects, and detailed recommendations about thresholding and correcting for multiple comparisons. We also hope to have renewed the value of exploratory research, and suggested analysis strategies such as effect size estimation, use of parcellations, and specification curve analysis. Finally, we provided initial practical guidance to help researchers engage in best practices that facilitate transparent and reproducible science, including preregistration and Registered Reports as well as comprehensive reporting.

Declaration of Competing Interest

None.