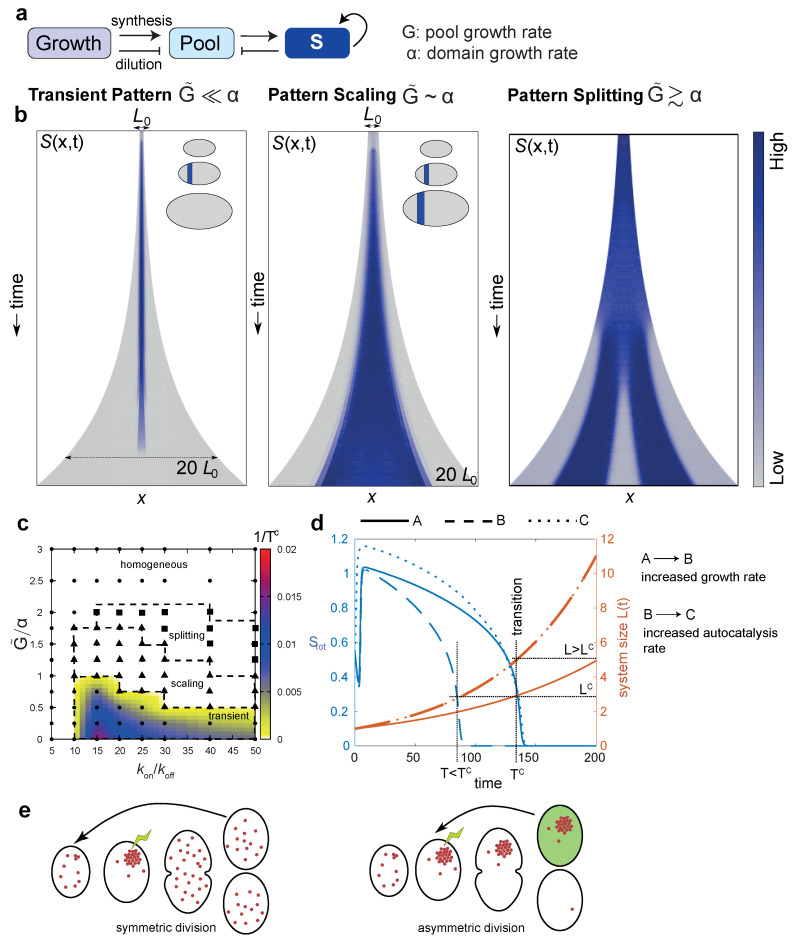
Figure 5.

Pattern scaling, splitting and transient pattern formation in growing domains. (a) Feedback motif for an activator–substrate system coupled to a growing domain. (b) (Left) When subunits are produced at a rate slower than the rate of domain growth, growth-induced dilution leads to transient pattern establishment. (Middle) When the production of subunit pool occurs at a rate comparable to system size growth, the pattern formed grows in proportion to system size, exhibiting a dynamic scaling behaviour. This is different from sequential pattern formation as the polarity is preserved during growth. (Right) In the case of strong autocatalysis of S, the pattern spontaneously splits. (c) Phase diagram for pattern formation as functions of pool growth rate relative to the system, $\tilde{G}/\alpha$, and $k_{\mathrm{on}}/k_{\mathrm{off}}$. Colormap denotes the inverse of the pattern lifetime, $1/T^c$. (d) Time evolution of structure size $S_{\mathrm{tot}}={\int }_0^{L}Sdx$ (blue) and system size L (red) for the case of transient pattern formation. The lifetime of the pattern $T^c$ is coupled to the system size at transition to the homogeneous state, $L^c$. They can be tuned independently of each other, for example, by changing growth rate $\alpha$ (case B) where only the transition time changes, or by changing autocatalysis rate (case C) where $T^c$ remains the same but transition happens at a different system size. (e) Tunability of pattern lifetime can be utilised as a control mechanism for symmetric and asymmetric cell division (in terms of polarity protein content). When the pattern is transient (left) the dissolution of the structure will make the daughter cells symmetric in fate, containing the same amount of polarity proteins. If the pattern persists (right) then the division will lead to asymmetric fate inheritance. Parameter values: $D_P=1$, $D_S=0.005$, ${\kappa }_0=0.85$, $S_0^2=10$, $\alpha =0.01$, $L\left(0\right)=1$, and total pool density $\int (P+S)dx/L=2$, with G and $k_{\mathrm{on}}/k_{\mathrm{off}}$ variable.