An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus

Abstract

This article investigates a family of approximate solutions for the fractional model (in the Liouville-Caputo sense) of the Ebola virus via an accurate numerical procedure (Chebyshev spectral collocation method). We reduce the proposed epidemiological model to a system of algebraic equations with the help of the properties of the Chebyshev polynomials of the third kind. Some theorems about the convergence analysis and the existence-uniqueness solution are stated. Finally, some numerical simulations are presented for different values of the fractional-order and the other parameters involved in the coefficients. We also note that we can apply the proposed method to solve other models.

1. Introduction, definitions and preliminaries

Fractional calculus has kept attracting the interest of many authors (see, for example, [5] and [6]). Some authors have observed that finding new fractional derivatives with different singular or non-singular kernels is essential to meet the need for modeling more real-world problems in different fields, such as biology, physics, engineering and others (see [14] and [39]).

Recently, the focus of many researchers is directed toward the modeling and analysis of various problems in bio-mathematical sciences. This branch of science represents many and distinct data about the biological phenomena such as the Ebola virus, the Bacterial cell and its distribution, Viruses, Nerve system and the transmission of its impulses, and so on (see [2], [11] and [30]). This has led to the modeling of many real-world issues including (for example) the aforementioned ones. Most (if not all) of these mathematical models that arise from many real-life problems are proposed and studied on the basis of biological experiences or statistical analysis. It is through some of these models that the interested scientist can studied and verify the behavior of these models in isolation in a modern laboratory-type biology experiment (see [3], [8], [20], [24] and [31]).

One of the advantages of mathematical modeling of various biological phenomena is that the mathematical model is represented as a mathematical function in time and the involved parameters. Hence, in this case, we can find the exact solutions to the model and also the parameters that affect this model can be controlled appropriately (see [17], [18], [19], [20]).

We begin by introducing the following definition which will be needed in our fractional-order epidemiological model of the Ebola virus.

Definition 1

The Liouville-Caputo derivative operator D^ν of fractional-order ν is defined in the following form (see [23] and [28]; see also the recent survey-cum-expository review article [35]):

$$D^{\nu }\phi \left(t\right)=\frac{1}{\Gamma (k-\nu )}{\int }_0^t\frac{{\phi }^{\left(k\right)}\left(\tau \right)}{{(t-\tau )}^{\nu -k+1}}d\tau$$

$$(\nu >0;k-1<\nu \leqq k;k\in \mathbb{N}:=\{1,2,3,\cdots \};t>0).$$

Here, in this article, we present a numerical study to solve the following fractional-order epidemiological model of the Ebola virus [9]:

$$D^{\nu }S\left(t\right)=-\alpha S\left(t\right)I\left(t\right)+\beta R\left(t\right)-\gamma N,S\left(0\right)={\tilde{s}}^0,$$ (1)

$$D^{\nu }I\left(t\right)=\alpha S\left(t\right)I\left(t\right)-ϵI\left(t\right)-\delta I\left(t\right),I\left(0\right)={\tilde{i}}^0,$$ (2)

$$D^{\nu }R\left(t\right)=\delta I\left(t\right)-\beta R\left(t\right),R\left(0\right)={\tilde{r}}^0,$$ (3)

$$D^{\nu }D\left(t\right)=ϵI\left(t\right)+\gamma N,D\left(0\right)={\tilde{d}}^0,$$ (4)

where ν ∈ (0, 1]. In the above system, the main variables and coefficients are defined in the following table.

Symbol	definition	Symbol	definition
$S\left(t\right)$	The susceptible population	$\alpha$	The rate of infection with the disease
$I\left(t\right)$	The infected population	$\beta$	The rate of susceptibility
$R\left(t\right)$	The recovery population	$\gamma$	The rate of natural death
$D\left(t\right)$	The population died in the region	$ϵ$	The rate of death from the disease
$N$	The total population in the region	$\delta$	The rate of recovery from the disease

The Ebola virus disease (EVD) was discovered in the Democratic Republic of the Congo near the Ebola River (Africa) for the first time in 1976. It is a fatal disease with a rare outbreak (see, for details, [30]). The EDV infects people from time to time and causes disease outbreaks in some African countries due to the impact of the Ebola virus disease on humans and primates (such as monkeys, gorillas and chimpanzees). It is difficult for many biologists to determine the exact origin of the virus. However, by its comparison with and similarity to the nature and behavior of the Ebola virus with other viruses, it has been found that it is mostly transmitted from animals. Bats or non-human primates are believed to be the origin and source of the Ebola virus (see, for example, [4] and [26]). The transmission and infection of monkeys from animals that carry the virus and from monkeys it is then transmitted to humans and non-human primates. Generally speaking, the Ebola virus can infect humans in one of the following ways: Direct contact with humans, blood, body fluids, animal tissues, and through direct contact with body fluids of a sick person or a person who died from the Ebola virus disease. As the current onslaught of the Corona virus, which is referred to as COVID-19 (see, for details, [1], [27] and [29]), the Ebola virus is transmitted to other patients or the virus can pass through broken skin or mucous membranes in the eyes, nose and mouth when a person comes into contact with infected body fluids (or contaminated objects), but the Ebola virus is also transmitted through sexual contact with someone who has the virus or who has recovered from it (see [7]; see also the recently-published works [36] and [37] for the fractional-order modeling of other diseases).

In a recent investigation, Dokuyucu and Dutta [9] demonstrated the existence of the solution for the EVD model (1), (2), (3), (4) with the help of some fixed-point theorems and by using the Liouville-Caputo fractional derivative. In addition, they showed the uniqueness of the solution of this system under some specified initial conditions. Combined solutions for S(t), I(t), R(t) and D(t) can be found in [10] and [13].

The Chebyshev polynomials are a well-known family of orthogonal polynomials on the interval $[-1,1]$ that have many applications. They are widely used because of their good properties in the approximation of functions. So the main aim of this study is to implement the Chebyshev spectral collocation method (CSCM) in order to solve the EVD model given by (1) to (4) and to show that CSCM greatly simplifies this model to a non-linear system of algebraic equations which becomes solvable by using any of the readily available numerical methods and techniques. In order to achieve this aim, we will use some advantages of the CSCM for solving this class of models in which the Chebyshev coefficients for the solution can exist very easily after using the numerical programs. For this reason, this method is much faster than the other methods. Also, this method provides a numerical technique with high accuracy, exponential rates of convergence and easy to use in finite and infinite domains for different problems (see [21], [32] and [33]).

The main structure of this paper is as follows. In Section 2, the numerical scheme and its convergence analysis are presented. In Section 3, the implementation the proposed method and numerical simulation are given. In Section 4, the numerical results and discussion are introduced. Finally, in Section 5, the conclusion is presented.

2. Numerical scheme and its convergence analysis

The classical orthogonal Chebyshev polynomials of the third kind and of degree n, which are orthogonal on $[-1,1],$ can be derived from the following formula (see, for example, [25] and [34]):

$$P_n^{\left(3\right)}\left(x\right)=\frac{\text{cos}\left(\right(n+\frac{1}{2}\left)\phi \right)}{\text{cos}\left(\frac{1}{2}\phi \right)}(x=\text{cos}\left(\phi \right);0\leqq \phi \leqq \pi ).$$

In this section, we will use these functions on [0, ℏ], so we can construct the so-called shifted Chebyshev polynomials by using the linear transform $x=(2/\hslash )t-1$. This type of functions is denoted and defined as follows:

$${\overline{\mathbb{T}}}_n\left(t\right)=P_n^{\left(3\right)}((2/\hslash )t-1),$$

where

$${\overline{\mathbb{T}}}_0\left(t\right)=1\text{and}{\overline{\mathbb{T}}}_1\left(t\right)=(4/\hslash )t-3.$$

One of the most useful formulas involving ${\overline{\mathbb{T}}}_n\left(t\right)$ is the analytic form given by (Khader [15], Khader and Babatin [16]):

$${\overline{\mathbb{T}}}_n\left(t\right)=\sum _{k=0}^n{(-1)}^k{2}^{2n-2k}\frac{(2n+1)\Gamma (2n-k+1)}{{\hslash }^{n-k}\Gamma (k+1)\Gamma (2n-2k+2)}{t}^{n-k},(n=2,3,4,\cdots ).$$

The function Ω(t) ∈ L ₂[0, ℏ] can be approximated as a finite sum of $\{{\overline{\mathbb{T}}}_0\left(t\right),{\overline{\mathbb{T}}}_1\left(t\right),\cdots \}$ as follows:

$${\Omega }_m\left(t\right)=\sum _{\ell =0}^m{a}_{\ell }{\overline{\mathbb{T}}}_{\ell }\left(t\right).$$ (5)

Theorem 1

Khader and Saad [22]

Suppose that the function Ω(t) is so constrained that Ω″(t) ∈ L ₂[0, ℏ] and $|{\Omega }^{{}^{″}}\left(t\right)|\leqq \xi ,$ where ξ is a constant. Then the series (5) of the shifted Chebyshev expansion is uniformly convergent and:

$$|a_{\ell }|<\frac{\xi }{{\ell }^2},(\ell \in 1,2,\dots ).$$ (6)

Theorem 2

Khader and Saad [22] Suppose that Ω(t) ∈ C^m[0, 1]. Then the error in approximating the function Ω(t) by Ω_m(t) by using the formula (5) can be bounded by:

$$\parallel \Omega \left(t\right)-{\Omega }_m\left(t\right)\parallel \leqq \frac{\wp {\Delta }^{m+1}}{(m+1)!}\sqrt{\frac{\pi }{2}}\text{and}\wp ={\text{max}}_{t\in [0,1]}{\Omega }^{(m+1)}\left(t\right)$$ (7)

$$(\Delta =\text{max}\{t_0,t-t_0\}).$$

In this section, we also give an approximate formula for D^νΩ_m(t) through the following theorem.

Theorem 3

( [12], [38] ) Suppose that the function Ω(t) is approximated in the form (5). Then D^ν(Ω_m(t)) can be defined by:

$$\begin{array}{ccc}\hfill D^{\nu }\left({\Omega }_m\left(t\right)\right)& =& \sum _{i=\lceil \nu \rceil }^m\sum _{k=0}^{i-\lceil \nu \rceil }{a}_i{{\rm Y}}_{i,k}^{\left(\nu \right)}{t}^{i-k-\nu }\text{and}\hfill \\ \hfill {{\rm Y}}_{i,k}^{\left(\nu \right)}& =& \frac{{(-1)}^k{2}^{2i-2k}(2n+1)(2i-k)!(i-k)!}{{\hslash }^{n-k}(k!)\Gamma (2i-2k+2)\Gamma (i-k+1-\nu )}.\hfill \end{array}$$ (8)

3. Implementation the proposed method and numerical simulation

We will now implement the Chebyshev spectral collocation method to solve numerically the EVD model in (1), (2), (3), (4) as follows:

$$\begin{array}{cc}& S_m\left(t\right)=\sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t\right),I_m\left(t\right)=\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right),\hfill \\ & R_m\left(t\right)=\sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t\right)\text{and}{D}_m\left(t\right)=\sum _{k=0}^m{d}_k{\overline{\mathbb{T}}}_k\left(t\right).\hfill \end{array}$$ (9)

By using (1), (2), (3), (4), (9) and the formula (8), we obtain:

$$\sum _{k=1}^m\sum _{\ell =0}^{k-1}{s}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}^{k-\ell -\nu }=-\alpha \left(\sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)+\beta \left(\sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)-\gamma N,$$ (10)

$$\sum _{k=1}^m\sum _{\ell =0}^{k-1}{i}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}^{k-\ell -\nu }=\alpha \left(\sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)-(ϵ+\delta )\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)\right),$$ (11)

$$\sum _{k=1}^m\sum _{\ell =0}^{k-1}{r}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}^{k-\ell -\nu }=\delta \left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)-\beta \left(\sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t\right)\right),$$ (12)

$$\sum _{k=1}^m\sum _{\ell =0}^{k-1}{d}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}^{k-\ell -\nu }=ϵ\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)\right)+\gamma N.$$ (13)

These last (10), (11), (12), (13) will be collocated at m nodes $t_p,p=0,1,\dots ,m-1$ as follows:

$$\begin{array}{ccc}\hfill \sum _{k=1}^m\sum _{\ell =0}^{k-1}{s}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}_p^{k-\ell -\nu }& =& -\alpha \left(\sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)\hfill \\ & & +\beta \left(\sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)-\gamma N,\hfill \end{array}$$ (14)

$$\begin{array}{ccc}\hfill \sum _{k=1}^m\sum _{\ell =0}^{k-1}{i}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}_p^{k-\ell -\nu }& =& \alpha \left(\sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)\hfill \\ & & -(ϵ+\delta )\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right),\hfill \end{array}$$ (15)

$$\sum _{k=1}^m\sum _{\ell =0}^{k-1}{r}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}_p^{k-\ell -\nu }=\delta \left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)-\beta \left(\sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right),$$ (16)

$$\sum _{k=1}^m\sum _{\ell =0}^{k-1}{d}_k{{\rm Y}}_{k,\ell }^{\left(\nu \right)}{t}_p^{k-\ell -\nu }=ϵ\left(\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t_p\right)\right)+\gamma N.$$ (17)

In addition, the associated initial conditions can be expressed by substituting from Eq. (9) therein. We are thus led to the following four equations:

$$\begin{array}{ccc}& & \sum _{k=0}^m{(-1)}^k(2k+1)s_k={\tilde{s}}^0,\sum _{k=0}^m{(-1)}^k(2k+1)i_k={\tilde{i}}^0,\hfill \\ & & \sum _{k=0}^m{(-1)}^k(2k+1)r_k={\tilde{r}}^0\text{and}\sum _{k=0}^m{(-1)}^k(2k+1)d_k={\tilde{d}}^0.\hfill \end{array}$$ (18)

Finally, (14), (15), (16), (17), together with the four equations in (18), give rise to a non-linear system of $4(m+1)$ algebraic equations. This system of algebraic equations will be solved for the following unknowns:   $s_k,i_k,r_k,d_k(k=0,1,\cdots ,m)$ by using the Newton-Raphson iteration method (NIM).

4. Numerical results and discussion

In this section, we solve the EVD model numerically by implementing the given method and demonstrate our solution by means of Figures 1–6. We consider Eqs. (1) to (4) with different values of ν, m, α, β, γ, δ, ϵ, N, and ℏ, as well as ${\tilde{s}}^0,$ ${\tilde{i}}^0,$ ${\tilde{r}}^0$ and ${\tilde{d}}^0.$

In Fig. 1 , we compare the approximate solutions (9) and the numerical solution based on the finite difference method by using the program Mathematica for the specific value $\nu =1$. The other parameters are taken as $\alpha =0.001,\beta =0.002,\gamma =0.01,ϵ=0.006,\delta =0.004,\hslash =20,$ and $N=10$. The initial values, $S\left(0\right)=70,I\left(0\right)=2,R\left(0\right)=0$ and $D\left(0\right)=0,$ are used here.

Fig. 1.

Graph of the comparison between the approximate solutions (9) and the numerical solutions at $m=21,\nu =1,\alpha =0.001,\beta =0.002,\gamma =0.01,ϵ=0.006,\delta =0.004$ and $N=10$. (Solid color: Approximate solutions; Dashed color: Numerical solutions). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

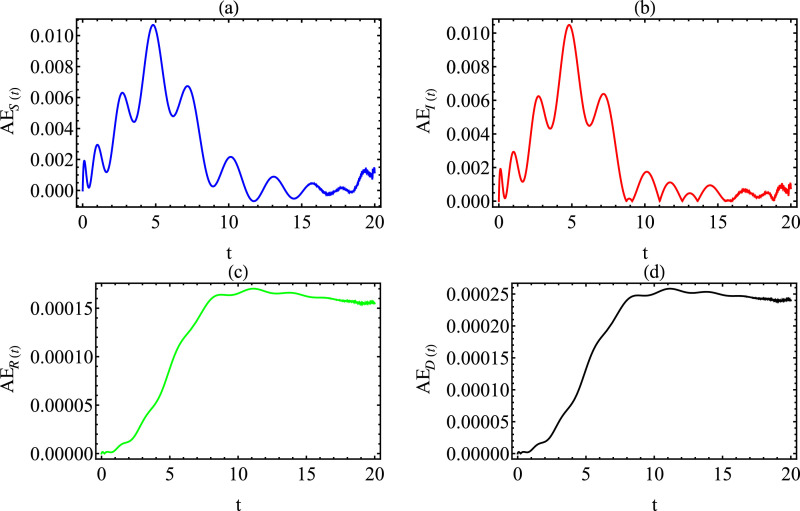
In Fig. 2 , we show the absolute error between the approximate solutions (9) and the numerical solution for the same parameters as in Fig. 1, but for $N=100$. From these two figures (Figs. 1 and (2), we can observe that the approximate solutions are very much in agreement with the corresponding numerical solutions. The comparisons are made with the integer-order derivative. In fact, we also show satisfaction with the effective and accuracy of the results involving derivative of non-integer order. Since most of the models do not have the exact solutions and also most of the similar programs are usually not capable of generating numerical solutions, so we need to verify the accuracy of the results by using some procedure. We can check the accuracy of the results by defining the residual error function (RE_f) as follows:

$${\text{RE}}_{\mathrm{f}}(S,I,R,t)=D^{\nu }S\left(t\right)+\alpha S\left(t\right)I\left(t\right)-\beta R\left(t\right)+\gamma N,$$ (19)

$${\text{RE}}_{\mathrm{f}}(S,I,t)=D^{\nu }I\left(t\right)-\alpha S\left(t\right)I\left(t\right)+ϵI\left(t\right)+\delta I\left(t\right),$$ (20)

$${\text{RE}}_{\mathrm{f}}(I,R,t)=D^{\nu }R\left(t\right)-\delta I\left(t\right)+\beta R\left(t\right),$$ (21)

$${\text{RE}}_{\mathrm{f}}(I,D,t)=D^{\nu }D\left(t\right)-ϵI\left(t\right)-\gamma N.$$ (22)

Fig. 2.

Graph of the absolute error function of (9) with $m=21,\nu =1,$  $\alpha =0.001,\beta =0.002,\gamma =0.01,ϵ=0.006,\delta =0.004$ and $N=100$.

Now, in view of the CSCM, the RE_f is given by:

$$\begin{array}{ccc}& & {\text{RE}}_{\mathrm{f}}(S,I,R,t)\hfill \\ & & =D^{\nu }\sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t\right)+\alpha \sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t\right)\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)-\beta \sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t\right)+\gamma N,\hfill \end{array}$$ (23)

$$\begin{array}{ccc}& & {\text{RE}}_{\mathrm{f}}(S,I,t)\hfill \\ & & =D^{\nu }\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)-\alpha \sum _{k=0}^m{s}_k{\overline{\mathbb{T}}}_k\left(t\right)\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)+(ϵ+\delta )\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right),\hfill \end{array}$$ (24)

$${\text{RE}}_{\mathrm{f}}(I,R,t)=D^{\nu }\sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t\right)\left(t\right)-\delta \sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)+\beta \sum _{k=0}^m{r}_k{\overline{\mathbb{T}}}_k\left(t\right),$$ (25)

$${\text{RE}}_{\mathrm{f}}(I,D,t)=D^{\nu }\sum _{k=0}^m{d}_k{\overline{\mathbb{T}}}_k\left(t\right)-ϵ\sum _{k=0}^m{i}_k{\overline{\mathbb{T}}}_k\left(t\right)-\gamma N.$$ (26)

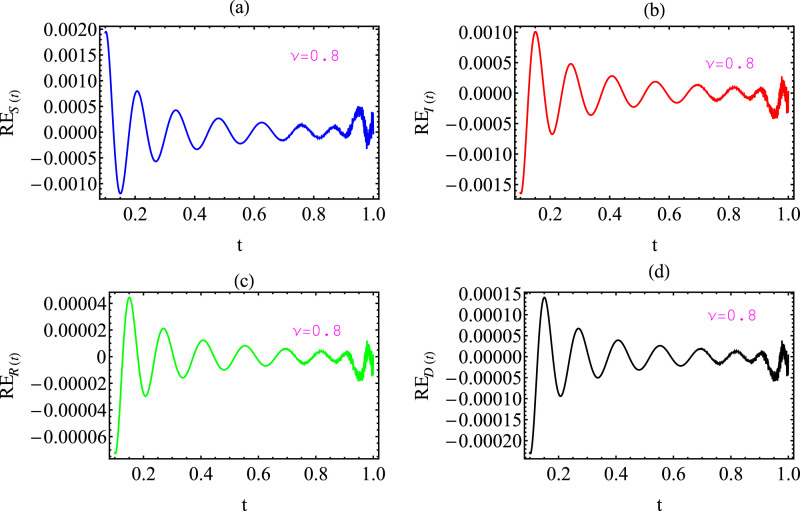
For computing the RE_f, we set $m=21,\alpha =0.01,\beta =0.008,\gamma =0.01,ϵ=0.006,\delta =0.004$ and $N=10,$ $\nu =0.8$; with $\hslash =1$ in Fig. 3 and $\hslash =5$ in Fig. 4 . The initial conditions in these two figures are taken to be $S\left(0\right)=10,I\left(0\right)=15,R\left(0\right)=0,$ and $D\left(0\right)=0.$ From the previous two figures (Figs. 3 and 4, we find that the results obtained in the fractional-order case indicate the accuracy and validity of the results presented in this work. In this way, we can verify the accuracy of the solutions in the case of a fractional order in which there is no exact solution.

Fig. 3.

Graph of the residual error function (23), (24), (25), (26) with $m=21,\alpha =0.01,$$\beta =0.008,\gamma =0.01,ϵ=0.006,\delta =0.004$ and $N=10$ with $\nu =0.8$ and $\hslash =1$.

Fig. 4.

Graph of the absolute error function of (9) and (17) with $m=21,\alpha =0.01,$$\beta =0.008,\gamma =0.01,ϵ=0.006,\delta =0.004$ and $N=10$ with $\nu =0.8$ and $\hslash =5.$

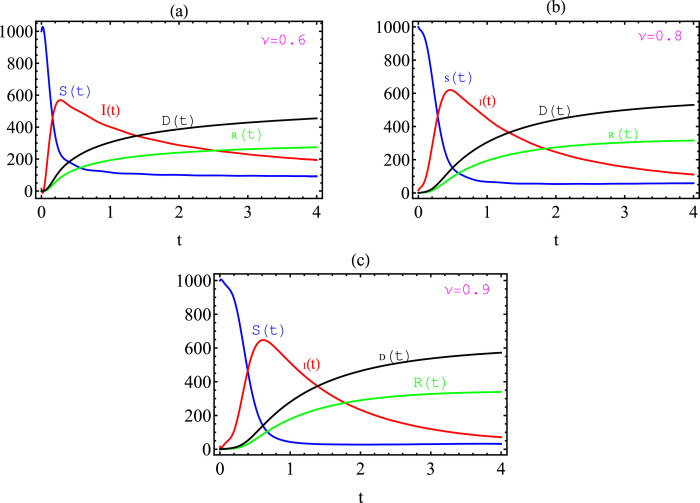
Next, in Figs. 5 and 6 , the behavior of the approximate solutions are studied with various specific values of the parameters as well as for different values of fractional-order. In Fig. 5, we take $\nu =0.6,0.8,0.9$ for the values $m=21,\alpha =0.01,\beta =0.02,\gamma =0.01,ϵ=0.6,\delta =0,\hslash =4$; and $N=1000$ with initial values given by $S\left(0\right)=1000,I\left(0\right)=15,R\left(0\right)=0$ and $D\left(0\right)=0.$ While in Fig. 6, we put $\nu =0.6,0.8,0.9$ for the values $m=21,\alpha =0.5,\beta =0.002,\gamma =0.01,ϵ=0.006,\delta =0,\hslash =20$; and $N=1000$ with the initial values given by $S\left(0\right)=70,I\left(0\right)=2,R\left(0\right)=0$ and $D\left(0\right)=0.$ Thus, from these Figs. 5 and 6, we note that the behavior of the approximate solutions is dependent strongly on the values of ν and the other chosen parameters.

Fig. 5.

Graph of the approximate solutions (9) with $\nu =0.6,0.8,0.9$ for the values $\alpha =0.01,\beta =0.02,\gamma =0.01,ϵ=0.6,\delta =0,m=21,$  $N=1000.$

Fig. 6.

Graph of the approximate solutions (9) with $\nu =0.6,0.8,0.9$ for the values $\alpha =0.5,\beta =0.002,\gamma =0.01,ϵ=0.006,\delta =0,m=21,$ and $N=1000$.

Finally, from all the figures which we present in this paper, we can confirm the efficiency of the proposed algorithm and its computationally favorable use for numerical treatment of the given model. We can also observe that all of the theoretical studies, which are concerned with the convergence analysis, are accomplished. In addition, the main and important note is that the behavior of the numerical solutions is in excellent agreement with the real meaning of the model and satisfies the same behavior of the components of the system S(t), I(t), R(t), D(t) via the increasing or decreasing numbers of each of these variables.

5. Conclusion

In our present investigation, we have proposed and applied a numerical method in order to successfully convert the fractional epidemiological model of the Ebola virus into a non-linear system of algebraic equations. The idea is to find expansions of the solutions by using the Chebyshev functions of the third kind. We then have made use of one of the known numerical methods, the Newton-Raphson method, for solving the resulting non-linear algebraic system. The accuracy of the approximate solutions was verified for our usage of the proposed method by closely comparing the approximate solutions with the numerical solutions resulting by using the computer program package Mathematica. In the case of the classical Ebola system (that is, in the case when $\nu =1$), as well as in the case of its fractional-order model, the residual error function is calculated. In all of the cases, we have found a remarkably good agreement. Finally, the behavior of the fractional epidemiological Ebola system was illustrated by assigning different values to the order of the fractional derivative as well as for different values of the other parameters involved. Several numerical simulations and illustrative graphical demonstrations have also been presented in this investigation. The applied techniques in this article show that their effect and power can be extended to other fractional-order models and the non-linear evolutions equations.

CRediT authorship contribution statement

H.M. Srivastava: Conceptualization, Methodology, Writing - review & editing. Khaled M. Saad: Writing - original draft, Conceptualization, Methodology, Software. M.M. Khader: Writing - original draft, Conceptualization, Methodology, Software.

Declaration of Competing Interest

The authors declare that they have no conflicts of interest.