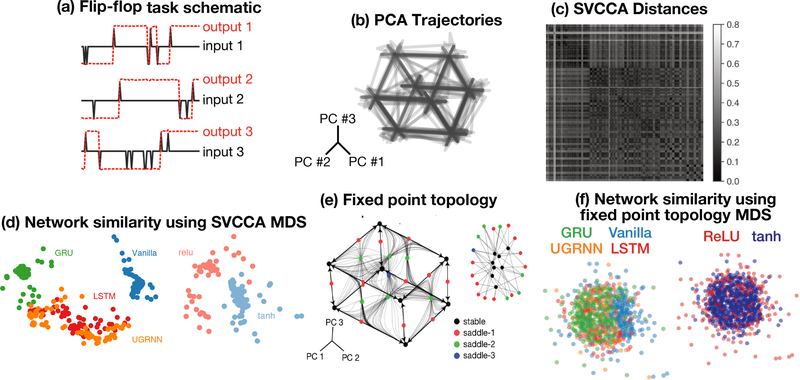
Figure 1:

3-bit discrete memory. a) Inputs (black) of −1 or 1 come in at random times while the corresponding output (dashed red) has to remember the last non-zero state of the input (either +1 or −1). b) Example PCA trajectories of dynamics for an example architecture and activation function. c) Dynamics across networks are compared via SVCCA and given a distance (one minus the average correlation coefficient), yielding a network-network distance matrix. d) This distance matrix is used to create a 2D embedding via multidimensional scaling (MDS) of all networks, showing clustering based on RNN architecture (left) and activation function (right). e) Topological analysis of a network using fixed points. First, the fixed points of a network’s dynamics are found, and their linear stability is assessed (left, black dots - stable fixed points, red - one unstable dimension, green − 2 unstable dimensions, blue − 3 unstable dimensions. By studying heteroclinic and homoclinic orbits, the fixed point structure is translated to a graph representation (right). f) This graph representation is then compared across networks, creating another network-network distance matrix. The distance matrix is used to embed the network comparisons into 2D space using MDS, showing that the topological representation of a network using fixed point structure is more similar across architectures (left) and activation functions (right) than the geometry of the network is (layout as in 1d).