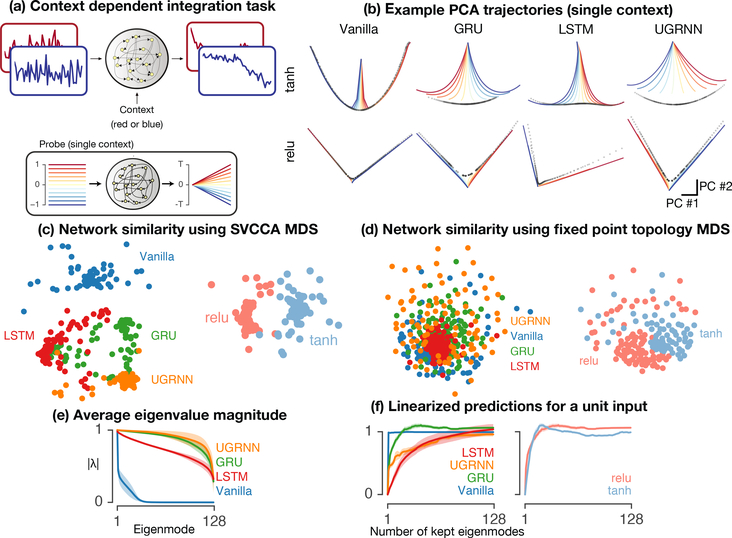
Figure 3:

Context-Dependent Integration. a) One of two streams of white-noise input (blue or red) is contextually selected by a one-hot static context input to be integrated as output of the network, while the other is ignored (blue or red). b) The trained networks were studied with probe inputs (panel inset in a), probes from blue to red show probe input). For this and subsequent panels, only one context is shown for clarity. Shown in b are the PCA plots of RNN hidden states when driven by probe inputs (blue to red). The fixed points (black dots) show approximate line attractors for all RNN architectures and nonlinearities. c) MDS embedding of SVCCA network-network distances comparing representations based on architecture (left) and activation (right), layout as in Fig. 1d. d) Using the same method to assess the topology of the fixed points as used in the sine-wave example to study the topology of the input-dependent fixed points, we embedded the network-network distances using the topological structure of the line attractor (colored based on architectures (left) and activation (right), layout as in Fig. 1d). e) Average sorted eigenvalues as a function architecture. Solid line and shaded patch show mean ± standard error over networks trained with different random seeds. f) Output of the network when probed with a unit magnitude input using the linearized dynamics, averaged over all fixed points on the line attractor, as a function of architecture and number of linear modes retained. In order to study the the dimensionality of the solution to integration, we systematically removed the modes with smallest eigenvalues one at a time, and recomputed the prediction of the new linear system for the unit magnitude input. These plots indicate that the vanilla RNN (blue) uses a single mode to perform the integration, while the gated architectures distribute this across a larger number of linear modes.