High-Resolution Diffusion Measurements of Proteins by NMR under Near-Physiological Conditions

Abstract

Measuring the translational diffusion of proteins under physiological conditions can be very informative, especially when multiple diffusing species can be distinguished. Diffusion NMR or diffusion-ordered spectroscopy (DOSY) is widely used to study molecular diffusion, where protons are used as probes, which can be further edited by the proton-attached heteronuclei to provide additional resolution. For example, the combination of the backbone amide protons (¹H^N) to measure diffusion with the well-resolved ¹H/¹⁵N correlations has afforded high-resolution DOSY experiments. However, significant amide-water proton exchange at physiological temperature and pH can affect the accuracy of diffusion data or cause complete loss of DOSY signals. Although aliphatic protons do not exchange with water protons and thus are potential probes to measure diffusion rates, ¹H/¹³C correlations are often in spectral overlap or masked by the water signal, which hampers the use of these correlations. In this report, a method was developed that separates the nuclei used for diffusion (alpha protons, ¹H^α) and those used for detection (¹H/¹⁵N and ¹³C’/¹⁵N correlations). This approach enabled high-resolution diffusion measurements of polypeptides in a mixture of biomolecules, thereby providing a powerful tool to investigate coexisting species under physiological conditions.

Graphical Abstract

Proteins in cells exist in the crowded milieu of biomolecules under physiological conditions.^1,2 Because translational diffusion rates provide information on the size, shape, and neighboring environment of molecules, diffusion measurements under physiological conditions provide insight into native protein function. Owing to the rich information that the diffusion rates provide, many techniques have been developed to measure molecular diffusion.^3–6 However, when a sample contains a mixture of different molecules or if a molecule exists in multiple conformations, it is difficult to determine the diffusion rate of each species separately.

Diffusion NMR^7–10 is a powerful technique to measure molecular diffusion rates. Because the diffusion dimension can be appended to chemical shift dimensions to provide additional resolution when required, diffusion NMR is also called diffusion-ordered spectroscopy (DOSY).^11,12 In a typical DOSY experiment, the diffusion delay is sandwiched between the encoding and decoding gradients. In the absence of diffusion during the diffusion delay period, the encoding and decoding gradients form a perfect gradient-echo and a strong DOSY signal is observed. When diffusion takes place during this delay, the location-dependent gradient-encoded phase is scrambled and an imperfect gradient-echo generates a weaker DOSY signal. The extent of gradient encoding/decoding, which depends on the gradient strength and gyromagnetic ratio of nuclear spins, and the amount of diffusion, which depends on the diffusion delay and molecular diffusion rates, combine to define the DOSY signal intensities.

DOSY sequences can be combined with multidimensional frequency labeling for high-resolution diffusion measurements. Initially, ¹H-DOSY was combined with two-dimensional (2D) ¹H-correlation spectroscopy (¹H-DOSY-¹H-COSY)¹³ or 2D ¹H-total correlation spectroscopy (¹H-DOSY-¹H-TOCSY)¹⁴ to give 2D spectra separated by molecular size. Similar experiments also enabled the determination of diffusion coefficients of individual molecules in a mixture, because the well-resolved 2D cross-peaks associated with particular molecules could be analyzed to provide individual diffusion coefficients.^{14,15 1}H-DOSY combined with heteronuclear single quantum coherence,^16,17 which we call ¹H-DOSY-¹H/¹³C-HSQC to be consistent with other nomenclature, or heteronuclear multiple quantum coherence (¹H-DOSY-¹H/¹³C-HMQC)^18,19 has also enabled efficient analysis of diffusion rates for species in complex mixtures.

Protein NMR takes advantage of heteronuclear correlations to achieve residue-specific information. Observation of backbone amide ¹H/¹⁵N correlations in a protein is commonly obtained because these correlations are well resolved and are clearly separated from the water signal. Thus, ¹H^N-DOSY has been combined with HMQC (¹H^N-DOSY-¹H/¹⁵N-HMQC) or HSQC (¹H^N-DOSY-¹H/¹⁵N-HSQC) (Figure 1a) for many applications.²⁰ For example, ¹H/¹⁵N-detected ¹H^N-DOSY was employed to observe apomyoglobin after suppressing the signals from small molecules in a cell lysate,¹⁶ to monitor protein folding and association of collagen-like peptides,²¹ to analyze residue-specific proton exchange rates between amides and water,^22,23 to identify the cleaved fragments of Engrailed 2 protein,²⁴ and to simultaneously determine the diffusion rates of both the folded and unfolded states of an SH3 protein.²⁵

Figure 1.

Diffusion NMR spectra obtained using distinct diffusion and detection probes. Diffusion measurement or diffusion-ordered spectroscopy (DOSY) was performed at pH 7.4 and 35 °C on a peptide and alpha-synuclein (αS) at an encoding/decoding gradient value of 5.8 G/cm. (a) Diffusion measurement on amide protons followed by ¹H/¹⁵N frequency labeling. Diffusion measurement on alpha protons followed by (b) ¹H/¹⁵N and (c) ¹³C’/¹⁵N frequency labeling. Black curved arrows inside each scheme show magnetization transfer pathways.

¹H^N-DOSY experiments can take advantage of amide-selective pulses to accelerate the T₁ relaxation of ¹H^N by maintaining the thermal bath of aliphatic protons,²⁶ enabling fast repetition of transients and thereby increasing the overall NMR sensitivity.²⁷ In principle, amide-selective excitation has no effect on water magnetization, and thus diffusion coefficients are not affected by proton exchange between amides and water. Amide-selective excitation under physiological conditions can accelerate T₁ relaxation by yet another mechanism: exchange between thermally-polarized water protons and amide protons.²⁸

However, at near physiological conditions, fast proton chemical exchange during the gradient-encoding, diffusion, gradient-decoding, and heteronuclear detection periods often causes complete loss of the ¹H/¹⁵N-detected ¹H^N-DOSY signals. If the water proton is not gradient-encoded, the DOSY signal will disappear upon proton exchange. This exchange-driven signal loss is illustrated for a peptide and the intrinsically disordered alpha-synuclein (αS) protein (Figure 1a). If the water proton is gradient-encoded, the diffusion rates can be overestimated.

A common feature of all diffusion NMR methods described above is that the protons used for diffusion recording and NMR data acquisition are the same. Here, we present a method that measures diffusion on alpha protons (¹H^α) that do not exchange with water protons, followed by transfer of the magnetization to the well-resolved ¹H/¹⁵N or ¹³C’/¹⁵N correlations for high-resolution detection under near physiological conditions (Figure 1b,c). Note that the ¹H^aliphatic-DOSY-¹H/¹³C-HSQC experiment would be free from the influence of amide-water proton exchange; however, it is often difficult to resolve and assign the ¹H/¹³C correlations because of severe spectral overcrowding,²⁹ especially for large proteins. Using the method described herein, diffusion analysis was performed successfully on a small peptide at pH 7.4 and 10 °C, the folded and unfolded states of the SH3 domain from Drosophila adaptor protein drk (drkN) at pH 8.0 and 20 °C, and αS interacting with lipid vesicles at pH 7.4 and 35 °C.

EXPERIMENTAL SECTION

Diffusion measurements of the peptide

All NMR experiments were performed on a 850 MHz Bruker NMR spectrometer equipped with a 5 mm z-axis gradient ¹H [¹³C,¹⁵N]-TCI cryogenic probe, except for the experiments used for SH3 backbone assignments. For the 1D diffusion experiments, a 2 mM RKY*Y*KR sample was prepared in a buffer containing 20 mM sodium phosphate (pH 7.4), 20 mM NaCl and 95%/5% H₂O/D₂O. The data for diffusion measurements were collected at 10 °C with a diffusion delay (Δ) of 150 ms, and encoding and decoding gradient width (δ/2) of 1.5 ms, and gradient strengths (Gauss/cm) of 5.1, 10.2, 14.1, 17.6, 21.0, 24.5, 28.1, and 31.8. The delay symbols are explained in Figure 2. For each gradient strength, 256 transients were averaged and the recycle delay was 2 s. For experiments with ¹H^N detection, 2,500 complex data points were sampled for 147 ms, and for experiments with ¹³C’ detection, 1,100 complex data points were sampled for 149 ms.

Figure 2.

Pulse sequences that separate nuclei used for diffusion and detection. Thin and thick black bars indicate 90° and 180° degree pulses, respectively, whereas the shaped lobes with E, Q and R on the top represent selective eburp, Q3, and reburp pulses, respectively.^32,33 Delays were set to τ₁ = 1.7 ms (= 1/4J_HαCα), τ₁’ = 1.25 ms (< 1/4J_HαCα), τ₂ = 4.7 ms (= 1/4J_C’Cα), τ₃ = 14 ms (= 1/4J_C’N), and τ₄ = 2.6 ms (= 1/4J_NH). Δ is the diffusion delay, δ/2 is the width of a gradient in the bipolar pulse pair and τ is the distance between the gradient pairs. All phases of pulses are omitted from the sequence. Diffusion was measured on ¹H^α followed by (a) ¹H/¹⁵N-HSQC and (b) ¹³C’/¹⁵N-HSQC pulse schemes. Detailed parameters of the pulse sequences in the absence and presence of the convection compensation scheme are described in Figure S1 and S2, respectively

Diffusion measurements of the drkN SH3 domain

For the high-resolution diffusion experiments on the drkN SH3 domain, a ¹³C/¹⁵N-enriched 1 mM SH3 sample was prepared in a buffer containing 20 mM sodium phosphate (pH 8.0), 20 mM NaCl, and 95%/5% H₂O/D₂O. 2D ¹H^α-DOSY-¹H/¹⁵N-HSQC experiments were performed with a diffusion delay (Δ) of 300 ms and gradient width (δ/2) of 1.5 ms at 20 °C. Five different gradient strengths (Gauss/cm) of 5.8, 10.8, 14.8, 18.7, and 22.6 were used to measure diffusion rates. Each experiment was acquired with a recycle delay of 2 s and a data matrix of 400 (t₁, ¹⁵N) × 2000 (t₂, ¹H) complex points and sweep widths of 2,400 (¹⁵N) and 14,800 (¹H) Hz. Sixteen scans were acquired for each FID, resulting in 10 h of data collection time for each gradient point. NMRPipe³⁰ and NMRFAM-SPARKY³¹ were used for data processing and analysis, respectively.

Diffusion measurements for probing the interaction between αS and SUV

1D ¹H^α-DOSY-¹H/¹⁵N-HSQC and ¹H^α-DOSY-¹³C’/¹⁵N-HSQC experiments without frequency labeling in the indirect dimension were recorded to measure the diffusion rate of 1 mM αS in the presence and absence of 1 μM SUV (5 mM lipid molecules, 5:3:2 DOPE/DOPS/DOPC; Avanti Polar Lipids, Alabaster, AL, USA, cat. no. 790304). The sample was prepared in a buffer containing 20 mM sodium phosphate (pH 7.4), 20 mM NaCl, and 95%/5% H₂O/D₂O, and the experiments were performed at 35 °C. A diffusion delay (Δ) of 300 ms and gradient width (δ/2) of 1.5 ms was used. Gradient strengths (Gauss/cm) of 5.8, 11.5, 15.8, 19.8, 23.7, 27.5, 31.6, 35.8, and 40.2 were used to measure the diffusion coefficients. For each gradient strength, 256 transients were averaged and the recycle delay was 3 s. For the ¹H^α-DOSY-¹H/¹⁵N-HSQC experiment, 2,500 complex data points (¹H^N) were sampled for 147 ms, and for the ¹H^α-DOSY-¹³C’/¹⁵N-HSQC experiment, 1,100 complex data points (¹³C’) were sampled for 149 ms.

To measure the diffusion coefficient of SUV at 35 °C, 1 μM SUV were prepared in the buffer for αS experiments described above. ¹H^aliphatic-DOSY with a diffusion delay of 300 ms was used to monitor the DOSY attenuation profile of lipid methylene protons resonating at 1–1.5 ppm. Gradient strengths (Gauss/cm) of 5.8, 11.5, 15.8, 19.8, 23.7, 27.5, 31.6, 35.8, and 40.2 were used. For each gradient strength, 256 transients were averaged and 5,000 complex data points (¹H) were sampled for 294 ms with a recycle delay of 3 s.

To measure the diffusion rate of dioxane, 5 mM 1,4-dioxane (Samchun, Pyeongtaek, Korea, cat. no. D1094) was added to the αS only, SUV only and αS + SUV samples described above and diffusion coefficients were measured at 35 °C. Gradient strengths (Gauss/cm) of 1.4, 2.8, 3.9, 4.8, 5.8, 6.7, 7.7, 8.7, and 9.8 were used and 5,000 complex data points (¹H) were sampled for 294 ms with a recycle delay of 3 s. To calibrate the gradient strengths, the diffusion coefficient of HDO in a 0.1%/99.9% H₂O/D₂O sample at 25 °C was set to 19.02 × 10^–10 m² s^–1.³⁴

The details on the preparation of the peptide, proteins and lipid samples are described in the experimental section of the supporting information (SI).

RESULTS

Pulse sequences for high-resolution diffusion NMR

We present two HSQC-edited ¹H^α-DOSY experiments. The first experiment involves a ¹H^α-DOSY followed by a ¹H/¹⁵N-HSQC (¹H^α-DOSY-¹H/¹⁵N-HSQC), where diffusion measurements of non-labile ¹H^α nuclei avoid complications from amide-water proton exchange while affording the higher resolution of ¹H/¹⁵N detection. Because the intra-residue magnetization transfer of H^α(i) → C^α(i) → N^H(i) → H^N(i) also involves an unwanted magnetization transfer to N^H(i+1), we have designed the magnetization transfer scheme to be H^α(i) → C^α(i) → C’(i) → N^H(i+1) → H^N(i+1) (Figure 2a), where the symbol in parenthesis denotes the relative residue position. Although chemical shift detection of the (i+1)-th residue is encoded with diffusion information of the i-th residue using the inter-residue magnetization transfer scheme, the coherences experience less T₂ relaxation when compared with detection via the intra-residue magnetization transfer scheme.^35–37

The diffusion measurement employs a stimulated-echo (STE) (Figure 2a) to store magnetization along the z-direction rather than the xy-plane during the diffusion delay, making the gradient-encoded magnetization experience T₁ rather than T₂ relaxation.³⁸ In addition, bipolar gradient pulse pairs (BPP; (+)-gradient → 180° pulse → (–)-gradient) (Figure 2a) were used for gradient encoding and decoding to minimize the ¹H-¹H nuclear Overhauser effect (NOE) during the diffusion delay, suppress artifacts from strongly coupled spin systems, reduce eddy currents, and refocus the deuterium lock signal.³⁹ Further, we introduced an unbalanced BPP (the (+)-gradient is scaled by (1+α) and (–)-gradient is scaled by (1–α)), which is known as the one-shot sequence,⁴⁰ to effectively eliminate signals that do not experience the 180° pulse in the BPP.

When the loss in NMR sensitivity due to amide-water proton exchange during the ¹H/¹⁵N data acquisition period (red box in Figure 2a) outweighs the sensitivity gain obtained by observing ¹H instead of ¹³C, diffusion measurements using ¹H^α-DOSY can be followed by ¹³C’/¹⁵N detection (¹H^α-DOSY-¹³C’/¹⁵N-HSQC) (Figure 2b) rather than the ¹H/¹⁵N detection (Figure 2a). Additionally, this experiment can be used when the ¹³C’/¹⁵N correlations are better resolved than the ¹H/¹⁵N correlations. Here, the magnetization flow is H^α(i) → C^α(i) → C’(i) → N^H(i+1) → C’(i), where the last two steps enable ¹⁵N frequency labeling.

Convection of solvent inside an NMR tube can complicate diffusion analysis. Because convection causes unidirectional translational motion of molecules, the convection-compensation (CC) sequence can be employed to negate the effect of convection in diffusion measurements.⁴⁴ This scheme, which is shown in Figure S2, modifies the DOSY sequence in the blue box of Figure 2a,b. The CC sequence compensates for convection but the NMR signal is reduced by 50%. The effect of convection in diffusion measurements should be checked when a regular 5 mm NMR tube is used with the temperature set above 30 °C and/or broadband decoupling applied.⁴⁵

To calculate diffusion coefficients from NMR experiments, the gradient-strength-dependent attenuation profile of DOSY intensities is measured. For the BPP-STE (Figure 2, S1) and BPP-STE-CC (Figure S2) experiments, the relevant Stejskal-Tanner equations⁴⁶ are

$$\begin{gathered} \text{BPP-STE}: \\ \ln \left(\frac{I\left(g\right)}{I\left(g_{\text{o}}\right)}\right)=\ln \left(\frac{I}{I_{\text{o}}}\right) \\ =-D[{\gamma }^2(g^2-{g_{\mathrm{o}}}^2){\delta }^2(\Delta +\frac{\delta \left({\alpha }^2-2\right)}{6}+\frac{\tau \left({\alpha }^2-1\right)}{2})] \end{gathered}$$ (1)

$$\begin{gathered} \text{BPP-STE-CC}: \\ \ln \left(\frac{I\left(g\right)}{I\left(g_{\text{o}}\right)}\right)=\ln \left(\frac{I}{I_{\text{o}}}\right) \\ =-D[{\gamma }^2(g^2-{g_{\mathrm{o}}}^2){\delta }^2(\Delta +\frac{\delta \left({\alpha }^2-2\right)}{3}+\tau ({\alpha }^2-1))] \end{gathered}$$ (2)

where g is the variable encoding and decoding gradient strength, g_o is the lowest gradient strength, I(g) is the NMR signal intensity at gradient strength g, D is the diffusion coefficient, γ is the proton gyromagnetic ratio, δ/₂ is the width of the gradient length, τ is the distance between the gradient pairs, α is the BPP imbalance factor,⁴⁰ and Δ is the diffusion delay. The expression inside the square bracket is often called the b factor, which is different between STE-BP and STE-BP-CC. The slope of the plot between the b factor and $\ln \left(\frac{I\left(g\right)}{I\left(g_{\mathrm{o}}\right)}\right)$ provides information on the diffusion coefficient. Normally, (b factor, $\ln \left(\frac{I\left(g\right)}{I\left(g_{\mathrm{o}}\right)}\right)$) data points are obtained for different g values and least squares fitting of the data points to a straight line provides the diffusion coefficient (Figures. 3, 4, and 5).

Figure 3.

Effect of amide-water proton exchange on the diffusion measurement of the RKY*Y*KR peptide at pH 7.4 and 10 °C. (a) Pulse schemes that are used to observe the effect of water perturbation on diffusion measurements. 1D DOSY experiment with amide selective pulses (¹H^N-DOSY), ¹H^N-DOSY with weak water saturation (¹H^N-DOSY-sat) and ¹H^N-DOSY with weak water saturation (CW) and a long recycle delay of 5 s (¹H^N-DOSY-long) were employed. The lobes with E, tr-E and R denote amide-selective eburp, time-reversed eburp and reburp pulses, respectively.³² The open rectangles above and below the horizontal lines indicate the bipolar gradient pulse pairs (BPP). The open lobes are crush gradients. (b) DOSY intensity attenuation profiles that illustrate the effect of water perturbation on diffusion measurements. Errors are calculated from the signal-to-noise ratio of NMR spectra. (c) Comparison of diffusion measurements performed by ¹H^N-DOSY and the experiments described in Figure 2, without frequency labeling in the indirect dimension.

Figure 4.

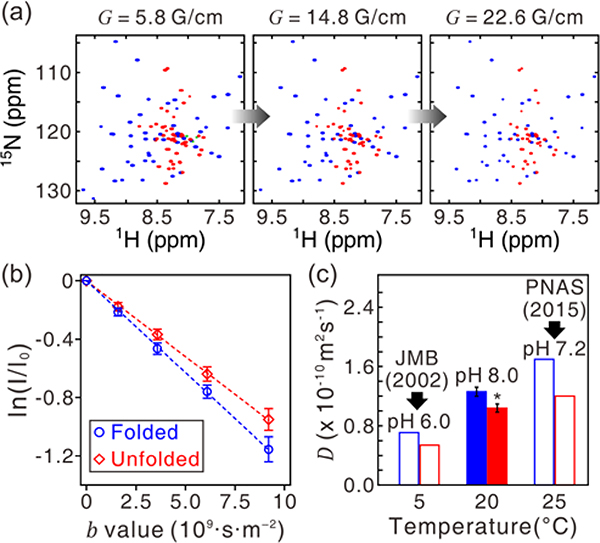
Simultaneous diffusion coefficient measurements of the folded and unfolded states of the drkN SH3 domain at pH 8.0 and 20 °C. (a) 2D ¹H^α-DOSY-¹H/¹⁵N-HSQC spectra of ¹³C/¹⁵N-enriched 1 mM SH3 domain with increasing gradient strengths. Signals from both the folded (blue) and unfolded (red) states are observed. Unassigned resonances are colored in green. The diffusion delay was set to 300 ms. (b) DOSY attenuation profile. Data points are the average of all well-resolved folded (n = 43) and unfolded (n = 35) peak intensities, where the error bars indicate ± 1σ of the intensities. (c) Comparison of the diffusion coefficients of the SH3 domain measured under different conditions. Diffusion coefficient of the folded state (*) is statistically different from that of the unfolded state (p < 0.001). The diffusion coefficients at pH 6.0 and 5 °C, and pH 7.2 and 25 °C are from Refs. 25 and 29, respectively.

Figure 5.

Probing the interaction between αS and lipid membranes under near physiological conditions of pH 7.4 and 35 °C. (a) DOSY attenuation profiles of ¹³C/¹⁵N-enriched 1 mM αS, and 1 mM αS with 5 mM lipid molecules (ca. 1 μM lipid vesicles). For each profile, results from the 1D ¹H^α-DOSY-¹H/¹⁵N-HSQC and ¹H^α-DOSY-¹³C’/¹⁵N-HSQC experiments obtained in two independently prepared samples were averaged. (b) DOSY attenuation profile of 5 mM 1,4-dioxane in water and with each sample described in (a). (c) DOSY attenuation profiles of the ¹H^α-DOSY-¹H/¹⁵N-HSQC experiment without the convection compensation scheme (CC) and with ¹⁵N decoupling, with neither CC nor decoupling, and with both CC and decoupling.

Effect of water saturation on the diffusion measurement of a peptide

We first tested how diffusion measurements are affected by water perturbation when employing amide protons as diffusion probes. We performed ¹H^N-DOSY in the absence and presence of weak water saturation during the diffusion delay (Figure 3a) on a six-residue RKY*Y*KR peptide, whose tyrosine residues (marked with asterisks) are ¹³C,¹⁵N-enriched. We then compared these results with the diffusion measurements performed with the pulse sequences described in the previous section. At pH 7.4 and 35 °C, the DOSY signal was only observed in the ¹H^α-DOSY-¹³C’/¹⁵N-HSQC experiment (Figure 2b) even when a low encoding/decoding-gradient strength was used (Figure 1). Thus, we performed all peptide experiments at pH 7.4 and 10 °C, where the amide protons (¹H^N) were detected. Regardless of the nuclei and experiment used for diffusion and detection, we observed nearly identical diffusion rates, except when ¹H^N-DOSY was performed with water saturation (Figure 3).

The correlation between the b factor (x-axis) and logarithm of DOSY signals (y-axis) is a straight line when the random translation of molecules is governed by a single diffusion coefficient (equations 1 and 2) and the initial magnetization is the same before each transient regardless of the encoding and decoding gradient strength applied. We observed a linear correlation when only amide-selective pulses were used in the diffusion measurement (¹H^N-DOSY) (Figure 3b). In contrast, weak ¹H saturation on water (¹H^N-DOSY-sat) during the diffusion delay introduced an element of nonlinearity and generated a steeper slope (Figure 3b). We ascribe this effect to the decrease in radiation-damping-induced T₁ relaxation rate of saturated water arising from the increase of gradient strength. This effect, in turn, decreases the T₁ relaxation rate of amides,²⁸ resulting in the decrease of the DOSY signal. When water protons were close to thermal polarization regardless of the applied gradient strengths by extending the recycle delay from 2 to 5s, the slope of the correlation decreased almost to the level of the ¹H^N-DOSY experiment without saturation (Figure 3b).

Note that there are a few mechanisms that can decrease the sensitivity of DOSY experiments without affecting the measured diffusion rate. For instance, the ¹H-¹H nuclear Overhauser effect (NOE) can decrease the intensity of the DOSY signal, especially when the BPP scheme is omitted.⁴⁷ In addition, labile protons from side chains that exchange with saturated water can reduce the signal-to-noise of DOSY by an exchange-relayed NOE. Additionally, signals from the gradient-encoded ¹H^Ns that experience proton exchange with water during the diffusion delay will be removed by the decoding gradient, unless the water protons are also gradient-encoded. In the latter case, the measured diffusion rate will have a mixed contribution from the amide-bearing molecule and water.

Comparison of the results from ¹H^N-DOSY without water saturation to ¹H^α-DOSY-¹H/¹⁵N-HSQC and ¹H^α-DOSY-¹³C’/¹⁵N-HSQC experiments with no chemical shift evolution in the indirect dimension revealed nearly an identical correlation between the b factor and logarithm of DOSY signals (Figure 3c). Thus, consistent results were obtained when diffusion measurements are not affected by amide-water proton exchange. Note that although the pulse sequences in Figure 2 apply weak water saturation during the diffusion delay to suppress the water signal, this does not affect the diffusion measurement on non-labile alpha protons.

Diffusion measurement on the folded and unfolded states of SH3 at high pH

Different conformations of a molecule can be discriminated by their distinct diffusion rates by high-resolution diffusion measurements. Using non-labile H^α protons as diffusion probes and using the ¹H/¹⁵N-HSQC experiment for detection (¹H^α-DOSY-¹H/¹⁵N-HSQC) (Figure 2a), diffusion rates of the folded and unfolded states of the ¹³C/¹⁵N-enriched drkN SH3 domain at pH 8.0 and 20 °C were separately determined (Figure 4). This 59-residue domain is located at the N-terminus of the adaptor protein drk, and is marginally stable and exchanges between its folded and unfolded states.⁴⁸ The exchange rate is slow (k_ex ~ 2 s^–1)^49,50 on the chemical shift and diffusion timescales.

With 1D ¹H^α-DOSY, an average diffusion rate of the folded and unfolded states will be observed, without any effect from amide-water proton exchange. When ¹H^α-DOSY was followed by an ¹H/¹⁵N-HSQC, which can resolve most of the ¹H/¹⁵N cross-peaks of the folded and unfolded states of SH3,⁴⁸ it was possible to determine the diffusion rate of each state separately (Figure 4). The gradient-strength-dependent attenuation profile of DOSY intensities was measured with the ¹H^α-DOSY-¹H/¹⁵N-HSQC experiment (Figure 4a). Each data point in Figure 4b was obtained by averaging the intensities of the well-resolved 43 (35) backbone amide cross-peaks of the folded (unfolded) states of the SH3 domain at different gradient strengths. Note that the larger error range with stronger gradients (Figure 4b) reflects the concomitant decrease in the DOSY signal-to-noise.

The diffusion coefficients of the unfolded and folded drkN SH3 domain were assessed previously by other diffusion experiments. Initially, the ¹H^N-DOSY-¹H/¹⁵N-HSQC experiment that shares the diffusion delay with a ¹⁵N-frequency-labeling period was used to measure the SH3 domain diffusion rate at pH 6.0 and 5 °C.²⁵ Under these conditions, no issues from amide-water proton exchange were present. In contrast, proton exchange may affect the measurement of the diffusion rate of the SH3 domain at pH 7.2 and 25 °C when using the ¹H^N-DOSY experiment. Thus, the ¹H^aliphatic-DOSY-¹H/¹³C-HSQC was used to measure the diffusion rate of the SH3 domain at this higher pH and temperature. The diffusion measurement was confined to H^β nuclei of a few alanine residues because these ¹H/¹³C cross-peaks are easy to assign, well-resolved, and reasonably strong in intensity.²⁹

The diffusion measurement of the drkN SH3 domain at pH 8.0 and 20 °C gave a diffusion coefficient for the folded state of (1.26 ± 0.06) × 10^–10 m² s^–1, whereas the diffusion coefficient of the unfolded state was (1.04 ± 0.06) × 10^–10 m² s^–1. Thus, the unfolded state diffuses ~17% more slowly than that of the folded state. This result is consistent with other experimental results at different pH and temperatures (Figure 4c).^25,29 On the other hand, reducing the diffusion delay minimizes the effect of any exchange processes on the measured diffusion rate. The temperature dependence of the diffusion coefficient was clearly seen (Figure 4c).^51–53

Probing protein-lipid interactions at near physiological conditions

Biomolecular interactions at near physiological conditions (pH 7.4 and 35 °C) were monitored using the pulse sequences described in Figure 2. Interaction between the N-terminal-acetylated αS and lipid membrane was observed by measuring the diffusion of αS in the presence and absence of small unilamellar vesicles (SUV). αS is a 140-residue protein that is present at high concentrations in presynaptic terminals of neurons.⁵⁴ Although αS is highly water-soluble and possesses the characters of an intrinsically disordered protein, the function of αS is closely related to its interaction with lipid membranes.^55–57

We collected αS diffusion data using the experiments in Figure 2 without ¹⁵N frequency labeling. The diffusion coefficient of a 1 mM αS sample was (8.06 ± 0.15) × 10^–11 m² s^–1, whereas on the addition of 5 mM phospholipid (DOPE:DOPS:DOPC = 5:3:2) SUV to the sample caused a change in the diffusion coefficient of αS to (7.39 ± 0.09) × 10^–11 m² s^–1 (Figure 5a). It is unlikely that αS experienced any amyloid formation under this condition.⁵⁸ In the presence of SUV, the αS diffusion rate decreased while the correlation between the b factor and DOSY intensities remained linear (Figure 5a), indicating that αS experienced multiple lipid binding and release cycles during the 300-ms diffusion period. The change in the diffusion rate indicates that ca. 10% of αS is bound to SUV at pH 7.4 and 35 °C. This percentage was estimated by assuming that the diffusion coefficient of αS in the presence of SUV is the weighted average of the diffusion coefficient of SUV (2.86 × 10^–11 m² s^–1) and free αS (Figure 5a) after taking in account the effect of viscosity and convection as explained in the following paragraphs. The methylene peaks at 1–2 ppm were monitored to measure SUV diffusion. Considering that the maximum number of αS that can bind to one SUV (30 nm in diameter; measured by DLS) is ca. 100 and that 5 mM lipid molecules corresponds to about 1 μM SUV,⁵⁹ at most 10% of the αS molecules present in the sample can bind to SUV at any instant. This indicates that most of the SUV surface was occupied by αS under the experimental conditions employed.

Although the crowded macromolecular environment in a sample can differentially affect the translational diffusion of αS and small chemicals,⁶⁰ the diffusion rate of a chemical was measured in different macromolecular environments to normalize the effect of viscosity as much as possible. Diffusion coefficients of 5 mM 1,4-dioxane measured in samples without macromolecules, with 1 mM αS and with both 1 mM αS and 5 mM lipid molecules gave values of 1.39 × 10^–9, 1.28 × 10^–9 m² s^–1 and 1.27 × 10^–9 m² s^–1, respectively (Figure 5b). The decrease in the diffusion rate of dioxane in the presence of macromolecules is ascribed to a change in bulk viscosity, and this was later reflected in the calculation of the diffusion coefficients from Figure 5a to minimize the effect of viscosity.

To investigate the effect of convection on diffusion, we performed diffusion measurements on a 1 mM αS sample inside a Shigemi tube in the presence and absence of convection compensation (CC; equation 2, Figure S2). Note that Shigemi tubes were used in all other experiments. Convection can be substantial when an experiment is performed at high temperature or if a broadband decoupling scheme is applied. Because we performed our (control) experiments on αS at 35 °C with ¹⁵N broadband decoupling in both ¹H^α-DOSY-¹H/¹⁵N-HSQC and ¹H^α-DOSY-¹³C’/¹⁵N-HSQC pulse schemes, it is important to check the effect of convection. The diffusion coefficient of free αS decreased by 1.8% when CC was introduced to the control experiment with decoupling (Figure 5c). To determine whether convection is caused mainly by decoupling, we omitted the decoupling scheme in the control experiment and observed a 1.5% decrease in the diffusion coefficient (Figure 5c). In summary, although the effect of convection is small when using Shigemi tubes, slightly faster diffusion can be measured because of convection at high temperatures with decoupling. In contrast, convection was not observed at 20 °C even when decoupling was applied.

When the effect from viscosity and convection were both considered, the diffusion coefficients of the lipid-free and lipid-containing αS samples were (8.60 ± 0.19) × 10^–11 and (7.94 ± 0.14) × 10^–11 m² s^–1, respectively. Because the diffusion measurements were performed on alpha protons, we assume that the measured coefficients are not influenced by amide-water proton exchange even at pH 7.4 and 35 °C.

DISCUSSION [I AM ADDRESSING THESE REVISIONS IN THE OTHER UPDATED DISCUSSIONFILE]

Under physiological conditions, fast proton chemical exchange during gradient-encoding, diffusion, gradient-decoding and frequency-labeling periods can lead to a complete loss of ¹H^N-DOSY signals. The ¹H^α-DOSY-¹H/¹⁵N-HSQC signal is not affected by proton chemical exchange during the first three periods, whereas ¹H^α-DOSY-¹³C’/¹⁵N-HSQC is not affected by chemical exchange during all periods.

Another high-resolution DOSY scheme that is relatively insensitive to amide-water proton exchange is worth mentioning. Initially, multidimensional diffusion experiments were designed to evolve the ¹⁵N chemical shifts during the diffusion delay.^20,25 The experiments were further developed to measure diffusion of large proteins by storing the gradient-encoded magnetization in the N_z state, because ¹⁵N has a longer T₁ relaxation time than ¹H. This experiment called heteronuclear stimulated echoes (X-STE)⁶¹ was modified to obtain ¹⁵N-chemical-shift information during the diffusion delay²⁴ and was also optimized for transverse relaxation.⁶²

N_z magnetization is not susceptible to amide-water proton exchange. Thus, during the diffusion delay, the X-STE signal will not decrease because of proton exchange. However, at least for the purpose of diffusion measurements at physiological conditions, we believe that our proposed method will show better performance because of the following reasons. First, the proposed method is not susceptible to proton exchange during the gradient encoding and decoding periods. Second, our method can be easily modified to include the convection-compensation scheme, which is necessary to check for the presence of convection at high (>30 °C) temperatures. Finally, under near physiological conditions of pH 7.4 and 35 °C DOSY signals can be completely lost even in the ¹H^α-DOSY-¹H/¹⁵N-HSQC experiment (Figure 1b), thereby requiring the use of the ¹H^α-DOSY-¹³C’/¹⁵N-HSQC experiment. We compared the performance of different high-resolution DOSY experiments in Figure S3 using the RKY*Y*KR peptide sample. The X-STE experiment shows superior sensitivity at 5 °C, where the solvent exchange is slow, whereas only the ¹H^α-DOSY-¹³C’/¹⁵N-HSQC signal was detected at 37 °C, where the solvent exchange is fast.

Because methyl protons provide good sensitivity and do not exchange with solvent, they are an attractive diffusion probe. However, resolution of ¹H-¹³C correlations may not be enough to discriminate multiple coexisting species in a sample, especially for disordered proteins. In a sample that contains αS and SH3, there are three different species; αS, the folded and unfolded states of SH3. Assume that we are interested in simultaneously determining the diffusion rates of αS and the unfolded state of SH3. The amide ¹H-¹⁵N correlations were generally well-resolved (Figure 6a), where the diffusion rate of each peak can be separately measured and averaged for different species, while the methyl ¹H-¹³C correlations of alanine residues significantly overlapped among each other, even with the constant-time evolution period of 53 ms in the ¹H-¹³C HSQC experiment (Figure 6b).

Figure 6.

Comparison of the resolution provided by the amide ¹H-¹⁵N and methyl ¹H-¹³C correlations of alanine residues in a mixture of proteins. 2D NMR spectra were separately obtained for 0.5 mM αS and 0.2 mM SH3 samples both at pH 6.0 and 20 °C and overlaid. (a) Overlay of the 2D ¹H-¹⁵N HSQC spectra. The folded (gray) and unfolded (blue) state of SH3, and αS (red) are shown in different colors. (b) Overlay of the double constant-time (53ms) ¹H-¹³C HSQC spectra for the unfolded (blue) state of SH3 and αS (red). Only the alanine methyl ¹H-¹³C correlations are shown that are expected to have good resolution among methyl groups.

As mentioned, when proton exchange is too fast for frequency labeling by the ¹H/¹⁵N-HSQC, we used ¹³C’ detection after the diffusion measurement on ¹H^α (i.e., ¹H^α-DOSY-¹³C’/¹⁵N-HSQC). Nonetheless, the ¹H^α-DOSY-¹H/¹⁵N-HSQC is more sensitive than the ¹H^α-DOSY-¹³C’/¹⁵N-HSQC when amide-water proton exchange is reasonably slow, because the NMR signal intensity is proportional to the gyromagnetic ratio of the nucleus and the design of the probe is usually optimized for ¹H detection. Thus, the choice of which experiment to use depends on experimental conditions.

In summary, we presented an NMR method that can measure the diffusion of proteins at high resolution under physiological conditions. By separating the nuclei used for diffusion (¹H^α) and those used for detection (¹H/¹⁵N and ¹³C’/¹⁵N correlations), the method can simultaneously determine the diffusion rates of coexisting species without artifacts from amide-water proton exchange. As more research focuses on studying biomolecules under physiological conditions in the milieu of biomolecular mixtures, we believe that the high-resolution DOSY experiments presented herein will become increasingly useful.