Abstract
Although studied for many years, there remain continued gaps in our fundamental understanding of cardiac kinematics, such as the nature and extent of heart wall volumetric changes that occur over the cardiac cycle. Such knowledge is especially important for accurate in-silico simulations of cardiac pathologies and in the development of novel therapies for their treatment. A prime example is myocardial infarction (MI), which induces profound, regionally variant maladaptive remodeling of the left ventricle (LV) wall. To address this problem, we conducted an in-vivo fiduciary marker-based study in an established ovine model of MI to generate detailed, time-evolving transmural in-vivo volumetric measurements of LV free wall deformations in the normal state, as well as up to 12 hours post-MI. This was accomplished using a transmural array of sonomicrometry crystals that acquired fiducial positions at ~250 Hz with a positional accuracy of ~0.1 mm, covering the entire infarct, border, and remote zones. A convex-hull method was used to directly calculate the Jacobian J(t) = ΔυES(t)/ΔVED from sonocrystal positions over the entire cardiac cycle, where ΔV is the volume of each convex polyhedral at end diastole (ED) (typically ~1cc) or end-systole (ES). We demonstrated significant in-vivo compressibility in normal functioning LV free wall myocardium, with JES = 0.85 ± 0.12. We also observed substantial regional variations, with the largest reduction in local myocardial tissue volume during systole in the base region accompanied by substantial transmural gradients. These patterns changed profoundly following loss of perfusion post-MI, with the apical region showing the greatest loss of volume reduction at ES. To verify that the sonocrystals did not affect local volumetric measurements, JES measures were also verified by non-invasive magnetic resonance imaging, exhibiting very similar changes in regional volume. We note that while our estimates of regional compressibility were in close agreement with the values previously reported for large animals, ranging from 5% to 20%, the direct, comprehensive measurements of wall compressibility presented herein improved on the limitations of previous reports. These limitations included dependency on the small local volumes used for analysis and often indirect measurement of compressibility. Our novel findings suggest that proper accounting for the myocardial effective compressibility at the ~ 1 cc volume scale can improve the accuracy of existing kinematic indices, such as wall thickening and axial shortening, and to simulate LV remodeling following MI.
Keywords: cardiac function, myocardium, kinematics, compressibility, perfusion
1. Introduction
Under normal physiological conditions, myocardial perfusion takes place via the coronary vasculature and the capillary bed. This is facilitated by relatively large vascular content in heart, wherein the vasculature constitutes 15–20% of the myocardial volume (Wacker et al., 2002) including both arterial and venous vascular systems. Not surprisingly, blood perfusion can modulate and be affected by myocardial kinematics. For example, it is generally accepted that the coronary blood supply is negligible during systole, as muscle contraction compresses the myocardial vascular beds. During this time, downstream blood is driven into the venous drainage and upstream blood is propelled retrogradely into epicardial vessels, impeding further coronary flow perfusion (Ramanathan and Skinner, 2005). On the other hand, ex-vivo studies in isolated and arrested hearts (May-Newman et al., 1994) have suggested that increasing perfusion pressure produces substantial radial thickening and increase in myocardial tissue volume (up to 15%) that is greatest at the endocardium. Such observations clearly demonstrate the strong interconnection between myocardial kinematics and perfusion, indicating that myocardium as a whole may not preserve volume during systolic or diastolic deformations.
The notion of in-vivo compressibility of the myocardial wall due to blood redistribution during systolic contraction is far from new (see Table 1). Scaramuccius (1695) appears to be the first study to hypothesize that intramyocardial coronary vessels “are squeezed empty by the contraction of myocardium”, and Porter (1898) provided supportive observations in a canine study. More recently, reductions of 20% of blood volume (measured as the difference between arterial inflow and great cardiac venous outflow) in the beating versus the arrested heart were reported (Vergroesen et al., 1987). Yin et al. (1996) reported very similar values for fluid extrusion from passive myocardial specimens under physiological pressures in a fluid bath using a digital subtraction angiographic method. Comparison of potassium-arrested end-diastolic to barium-arrested peak-systolic configurations with imaging methods yielded a 42% reduction of blood volume, with about three-quarters of this volume being ejected from smaller vessels (Judd and Levy, 1991). Substantial myocardial volume reductions (about 15–20% bulk volume reduction from diastole to systole) were reported based on the displacements of radio-opaque markers (Waldman et al., 1985) and suggested several mechanistic hypotheses for blood redistribution and myocardium volume reduction: (i) anatomical communication between coronary vessels and Thebesian veins may provide myocardium drainage to the ventricular cavities; (ii) extensive trabeculation of the endocardial surface may contain a substantial amount of “compressible” void space; and lastly, (iii) the dynamic mobility of the myolaminar sheet structure may allow for blood-filled spaces within the myocardium (Ashikaga et al., 2008). Regardless of underlying mechanisms, a comparison among the existing reports of myocardial compressibility is given in Table 1.
Table 1:
Comparisons between reported myocardial compressibility. Some of the studies included here dis not explicitly report values for the volume reduction. The values were calculated from the reported strain measurements.
| Study | Subject & Condition | Size of Local Volume Studied | Measurement Description |
|---|---|---|---|
| Porter (1898) Porter (1898) | Dog, in-vivo | Not reported | Not reported, but considerable reduction in intramyocardial volume |
| Waldman et al. (1985) | Dog, in vivo | < 0.1 cc | 15% reduction in volume |
| Vergroesen et al. (1987) | Goat, in vivo | Not reported | 20% reduction in volume |
| Judd and Levy (1991) | Rat, in vivo | LVFW | 42% reduction in volume |
| Villarreal et al. (1991) | Dog, in vivo | < 0. 1 cc | 13% reduction in volume |
| Yin et al. (1996) | Dog, ex vivo | Not reported | 20% reduction in volume |
| Mazhari et al. (2001) | Dog, in vivo | Not reported | 6% reduction in volume |
| Ashikaga et al. (2004) | Dog, in-vivo | ~ 1 cc | Comparison with end relaxation, 10% reduction |
| Ashikaga et al. (2008) | Dog, in vivo | < 0.1 cc | 20% reduction in volume |
| Zhong et al. (2010) | Human, in vivo | LV | 16% reduction in volume |
| Tsamis et al. (2011) | Sheep, in vivo | ~ 1 cc | 8% reduction in volume |
| Tsamis et al. (2012a) | Sheep, in vivo | ~ 1 c.c | 4% reduction in volume |
| Tsamis et al. (2012b) | Sheep, in vivo | ~ 1 c.c | 6% reduction in volume |
| McEvoy et al. (2018) | Pig, ex-vivo drained tissue | ~ 0.1 cc | 10% reduction in volume under confined compression test |
In-vivo cardiac kinematics have long been used as a critical biomarker for evaluating the progress of structural heart diseases, such as myocardial infarction (MI) and hypertension. Changes in the metrics like LV wall thickening and LV long-axis shortening during contraction are used to characterize alterations in the LV contractile pattern as a result of MI. In this connection, in-vivo compressibility of myocardium can have a major effect on the estimation of these metrics, including over-(or under) estimation of changes in LV shape and general kinematics. In particular, when the myocardial wall is treated as isochoric, contraction-induced wall thickening will be overestimated, as a compressible wall could sustain fiber shortening without significant bulging in the cross-fiber directions. Similarly, the incompressibility assumption results in an underestimation of LV shortening close to the apex, as compressible myocardium again exhibits less axial extension during contraction. Therefore, accounting for the in-vivo compressibility of myocardium becomes of paramount importance to accurately quantify LV kinematics, particularly for the case of infarcted hearts, where myocardial perfusion is significantly impaired. Apically-infarcted hearts do not contract in the apex, and these regions “inflate” instead due to systolic pressure. Interestingly, t]exact post-MI remodeling events are not completely clear; it has been suggested that infarct thinning is the dominant feature of infarct remodeling, while changes in in-plane dimensions are variable and secondary to the balance between thinning and stiffening (Richardson and Holmes, 2015). Irregardless of the exact sequelae, the triggered remodeling cascade following MI induces myocardial fibrosis that promotes significant compositional, structural, and functional changes from infarcted myocardium to scar tissue. Collectively, these changes are a result of substantially altered perfusion in the infarct and border zones, altering the normal in-vivo compressibility in these regions.
In addition to the above considerations, in-silico simulations of heart function require the integration of many components, including accurate descriptions of regional mechanical behavior of the normal and infarcted myocardium. While the presence of significant myocardial systolic compressibility has been known for at least many decades, its experimental measurement and incorporation into computational simulations has not yet been sufficiently explored in contemporary cardiac models. This is in part due to some confusion as to the exact values and uncertainty in the need — and the additional work required — to shift from more accepted incompressible formulations. To further explore what effects that compressibility may have on cardiac simulations, we have previously conducted in-silico cardiac functional studies. Specifically, we utilized a specialized compressible model that reproduced a unimodal compressible behavior of myocardium, wherein the reduction in JES was proportional to the amount of myofiber contraction (Soares et al., 2017). The results of this first study demonstrated that the myofiber active contraction stress was substantially overestimated under the assumption of tissue incompressiblity.
While the studies reported in Table 1 have consistently supported the existence of myocardial compressibility during systole, the need for more extensive experimental studies in the normal and post-MI states remain in order to clarify the nature and extent of this phenomenon. This is underscored by the persistent lack of direct measurements of volume changes in myocardium during the cardiac cycle, which are major limitations with the existing reports. Indeed, the reports on the wall compressibility are often based on indirect calculations from either local strain measurements or arterial and venous flow gradients that can be influenced by artifacts of such measurements. Also, a complete understanding of regional and transmural variations in the wall compressibility in normal and diseased hearts over the cardiac cycle is still elusive. In particular, an accurate calculation of these variations depends critically on a technique that allows for consistent measurements of volume change across different regions of LV myocardium; however, this has yet to be undertaken. Finally, once measurements of such variations are established for normal hearts, comparable studies in deceased hearts with controlled alterations in the regional perfusion will serve to advance our understanding of potential mechanisms of myocardial compressibility.
The present study was thus undertaken to better understand the localized alterations in myocardial compressibility in both the normal and post-MI heart using an established ovine model of MI. Our focus was on organ-level assessments, using measurement volumes of approximately 1 cc. This volume was chosen to allow for sufficient averaging of myocardium and to avoid the effects of local variations in the coronary vasculature. A sonomicrometry method was used to directly quantify local volume changes with the sonocrystal transducers laid out in a transmural distribution over the LV free wall. Sonomicrometry is a permanent fiducial marker technique appropriate for the study of long-term remodeling that existing noninvasive imaging modalities cannot achieve. To maximize measurement accuracy, a convex-hull technique was used to quantify the local Jacobian J of myocardial regions formed by local groups of sonocrystals directly from their positions. We defined J = 1 at local end diastole (ED) and the normalized local volume change at end systole (ES), denoted by JES. We validated the sonomicrometry results with those of cardiac magnetic resonance (CMR) tagging. Next, in the same animals, we studied the progressive regional changes in local myocardial volume from pre-MI to post-MI for a duration of up to 12 hours. To the best of our knowledge, the present work is the first specific study of in-vivo myocardial compressibility in the normal and infarcted heart.
2. Methods
2.1. Large animal model
A total of seven adult Dorset sheep with weights ranging 40-50 kg were used in this study. The MI was induced by ligating the left anterior descending (LAD) artery and the D2 branch, which consistently resulted in apical infarction (Fig. 1a). All animals were humanely treated in accordance with the University of Pennsylvania Institutional Animal Care and Use Committee (Protocol 13021226).
Figure 1.
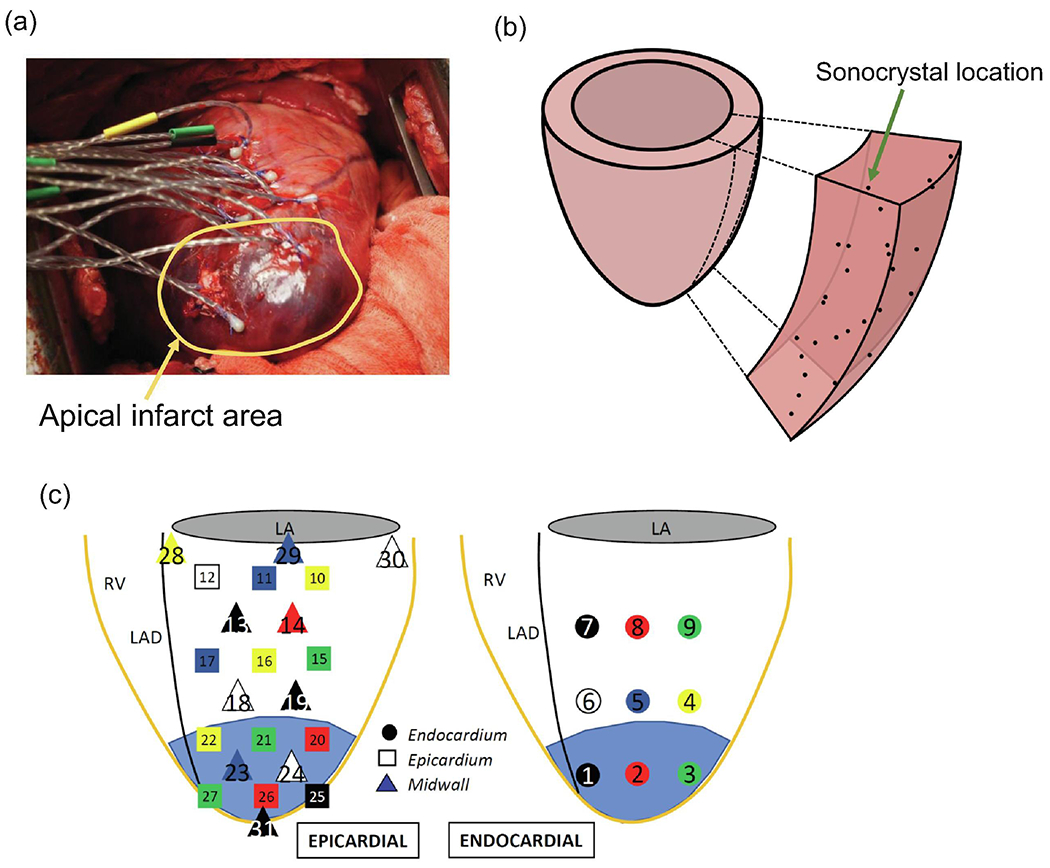
Sonocrystal array deployment in the ovine model. (b) Prolate spheroid wedge with sonocrystals locations. (c) Detail of transmural locations of the sonocrystal array spanning the full thickness of the LV free wall.
2.2. Sonomicrometry measurements
Sonomicrometry array localization (SAL) is a well-established imaging technique that uses small piezoelectric transducers (referred to as sonocrystals) to permanently label specific locations of myocardium (Gorman III et al., 1996; Jackson et al., 2002; Ratciiffe et al., 1995). In this study, sonocrystals (2 mm in diameter) were deployed into the LV free wall (LVFW) of ovine models of MI. Four male Dorset sheep were used in the sonocrystal study, in which a total of 31 sonocrystals that spanned the anterior and posterior regions of the LVFW were placed within the LV in apical, mid-height, and basal regions, referred to as apex, mid, and base throughout the paper (Fig. 1). To obtain a transmural description of volume changes, sonocrystals were divided into three groups, defined by their insertion into the endocardium, midwall, and epicardium regions (Fig. 1). Three-dimensional sonocrystal spatial positions were recorded at 250 Hz over multiple cardiac cycles and at several longitudinal time points, including pre-snare, immediately after snare, and post-snare (30 mins), denoted by T1, T2, and T3, respectively. The additional time points included post-snare (60 mins), post-snare (90 mins), and post-snare (12 hr).
2.3. Volume change quantification
The time-evolving position data of the sonocrystals enabled direct measurements of LV regional deformation within the sonocrystals array spatial domain. This is usually done by adopting a convective curvilinear coordinate system and discretizing and interpolating between the crystal locations using spline functions. However, our interest in this work was focused solely on proportional volume changes using J = Δυ/ΔV, where ΔV is the reference local volume and Δυ is the the local time-evolving volume beyond the reference point. The direct calculation of volume was advantageous as it eliminated the need to assume a specific form of the local three-dimensional strain field.
We first discretized the regions delimited by the sonocrystal array into polyhedral convex hulls (Preparata and Hong, 1977) (see Fig. 2a for a representative hull) and calculated the time-evolving volume of each hull over multiple cardiac cycles at each time point. The volume of each polyhedron was calculated from the divergence theorem using the following formula (Allgower and Schmidt, 1986):
| (1) |
where the sum is taken over all the faces (denoted by F) of the polyhedron, PF is an arbitrary point on face F, NF is the unit vector perpendicular to F pointing outside the polyhedron, and NF is the number of faces in each polyhedron. The volume confined by the sonocrystal array was divided into the three regions (apex, mid, and base), with nearly equal volumes at the organ-level (global) end-diastolic (ED) time point. In order to differentiate the dynamic volume changes in these regions, the reference volume for each region was chosen to be the maximum volume of the respective region occurring around the global ED. Therefore, the time point at which the maximum volume occurred was different for each region, referred to as the local ED (Fig. 2b). Similarly, the local end-systolic (ES) point of each region was identified as the time point at which the region reaches a minimum volume. This time point was close to but not the same as the global ES for the LV myocardial regions. Choosing the local ED as the reference configuration, the regional Jacobian was determined as a function of time using
Figure 2.
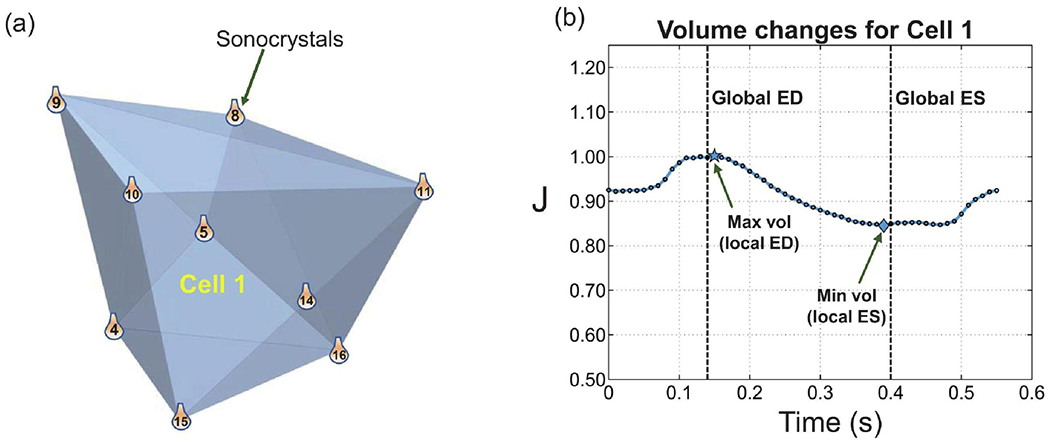
A representative convex hull constructed by nine sonocrystals and labeled as Cell 1. (b) Variation of the volume of Cell 1 within one cardiac cycle. The local and global ED and ES time points are denoted. The local ED and ES identify the time points at which the maximum and minimum volumes of Cell 1 occur, respectively.
The convex hull technique described above was suitable to clearly identify the apex, mid, and base regions and calculate the corresponding volume changes. However, to estimate a continuous transmural variation of JES, we used a prolate spheroidal wedge delimited by the sonocrystals. We reconstructed a wedge within the crystals and generated inflation and contraction modes of motion in the spheroidal system such that the predicted volume changes matched the data collected at sonocrystal sites. This led to a point-wise estimation of J in the transmural direction.
2.4. CMR validation
While well established, it has been speculated that the sonocrystal technique might produce unknown artifacts in local volume due to various interactions with the myocardium. Moreover, we were interested if any observed volume changes might also be observable in clinical studies using non-invasive methods. To this end, we utilized CMR tagging for additional validation of the sonomicrometry results (Axel and Dougherty, 1989; Ibrahim, 2011). Three male Dorset sheep were used for theCMR study. Spatial modulation of magnetization (SPAMM) was used for visualizing transmural myocardial movement and calculating volume changes. Visible tags with a grid pattern of magnetization saturation were created on the myocardial wall. The tags covering the regions of interest (apex, mid, base) were identified at the global ED point. Each region was further divided into three transmural depths (endo, mid, and epi). Volume changes were calculated by tracking tags’ intersection points on the boundary of each region and measuring relative increases or decreases of their in-between distances from one time frame to another.
3. Results
3.1. Regional and temporal variations in the compressibility in normal myocardium
All the three regions of the normal myocardial wall (base, mid, and apex) showed significant reductions in volume relative to their volumes at the local ED point (Fig. 3a). The apex and midwall regions exhibited slightly higher compressibility than the base region, which showed about 15% decrease in volume from the local ED to ES (Fig. 3a). Also, calculations from the deformation of the spheroidal wedge during the cardiac cycle demonstrated a progressive decrease in myocardial wall compressibility from the epi- to the endocardial surface (Fig. 3b). Our measurements suggested that some very local areas close to the endocardial surface may experience volume reduction up to 25% (Fig. 3b). The volume changes across the epicardial layer were also significant for some of the specimens, especially in the basal region (Fig. 3c). These results clearly corroborated established evidence that myocardium does not deform isochorically during the cardiac cycle.
Figure 3.
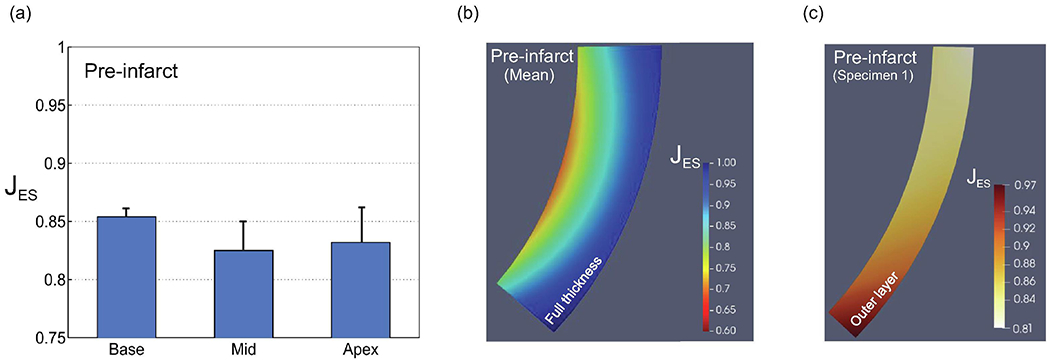
(a) Volume changes from local ED to local ES (JES) for healthy myocardium for basal, mid, and apical regions. (b) Average transmural variation of JES for healthy myocardium (n = 4). (c) Representative transmural variation of JES for epicardial layer (n = 1).
The temporal variation of volume reduction for apex, midwall and base regions were chosen from a representative healthy heart with a more drastic changes in J (Fig. 4a), where the local volume reduction in apical area reached as low as 60% at the ES time point. Despite the strong regional variations, the wall compressibility in healthy myocardium became progressively pronounced after the global ED point and reached its respective maximum at about the global ES point for all three basal, mid and apical regions (Fig. 4a). However, the apical and midwall regions achieved more than double the volume reduction compared to the base. Also, the basal and midwall regions tended to attain their maximum volume slightly earlier than the apical region (Fig. 4a). Finally, our mean estimates of volume changes calculated from the convex hull representation of the sonocrystal arrays agreed well with the corresponding calculations from the CMR tagging for apex, mid, and base regions (Table 2).
Figure 4.
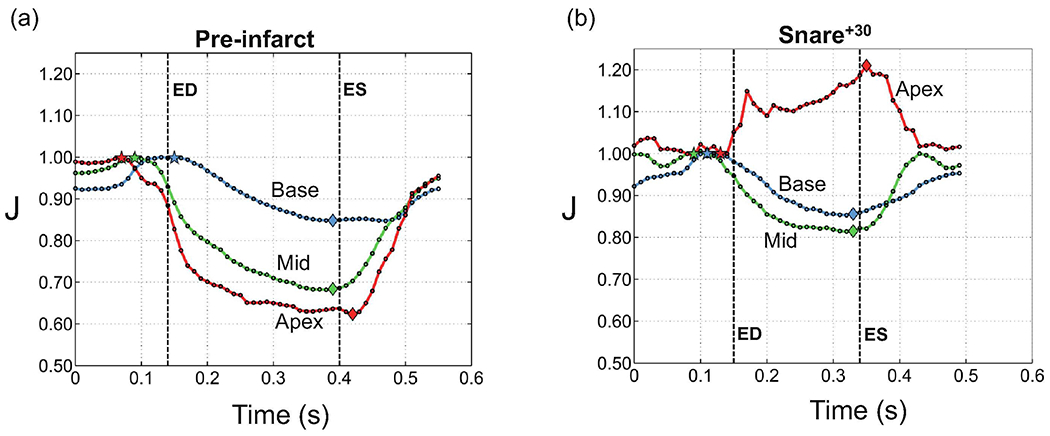
Temporal changes in the ventricular volume within a cardiac cycle for basal, mid and apical regions. (a) Pre infarct (T1), (b) 30 mins after infarct (T3). The results were chosen for a specimen that exhibits clear distinction between the regions although J values for the apex in this specimen was the largest recorded in our cohort. Note that ’ED’ and ’ES’ refer to global end-diastole and end-systole, respectively.
Table 2:
Average transmural volume changes (n=3) for endocardial (endo), midwall, and epicardial (epi) layers calculated from CMR SPAMM tagging. The calculations were done for basal, mid and apical ventricular regions.
| Volume change (JES) | ||||
|---|---|---|---|---|
| Base | Mid | Apex | Total Regions | |
| Endo | 0.83 | 0.84 | 0.90 | 0.86 |
| Midwall | 0.86 | 0.86 | 0.92 | 0.88 |
| Epi | 0.90 | 0.89 | 0.95 | 0.91 |
| Full Thickness | 0.86 | 0.86 | 0.92 | 0.88 |
3.2. Regional changes in compressibility: normal vs. post-MI
Time course analysis shows that MI impacted the ability of the infarcted myocardium to contract and be perfused by blood, even within 30 minutes following the snare (Fig. 4). Both the regional pattern and magnitude of the compressibility drastically changed within 30 minutes (Fig. 4b). The apical region containing the infarct area showed an opposite behavior, exhibiting volume expansion during systole. The mid region containing the border zone showed less pronounced volume reduction compared to the healthy case, while the basal region containing the remote region in the infarcted heart maintained nearly the same level of volume reduction after infarction. Interestingly, on average among all the four specimens, the largest change in the regional volume at the local ED was observed in the mid region, with about 10% increase in volume, while the apex, containing the infarct region, showed smaller changes (~6%) (Fig. 5a). In contrast, the basal region showed a slight decrease (~2%) in ED volume (Fig. 5a). The average changes in the regional compressibility showed a drastic increase in the apical, basal, and midwall regions by approximately 11%, 3%, and 1.5%, respectively (Fig. 5b), which were qualitatively similar to our observations from Fig. 5 (shown for one specimen).
Figure 5.
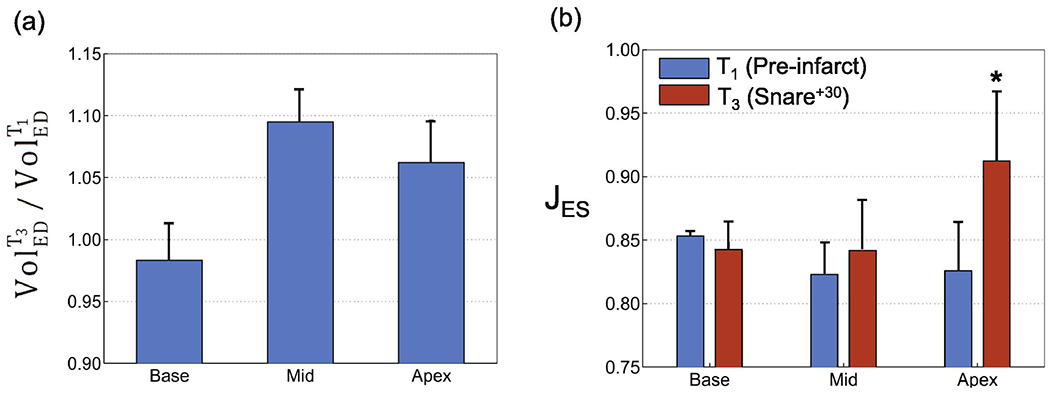
Changes in myocardial compressibility from pre-infarct (T1) to 30 mins post-infarct (T3) for basal, mid and apical regions. (a) T3 Volume/T1 Volume at end diastole (ED). (b) Comparisons of average volume reduction (J) for total ventricular wall. *p < 0.05 versus pre-infarct (T1) value.
3.3. Transmural changes in compressibility: normal vs. post-MI
In addition to regional differences, the transmural variations in the wall compressibility following MI were noteworthy (Fig. 6; shown for one specimen). While the normal heart had its strongest transmural gradient in the midwall region, the infarcted heart showed the strongest transmural gradient in the basal region, progressively decreasing towards the apical region and attaining minimal variation in the apex (Fig. 6). However, similar to the healthy heart, the infarcted heart exhibits the highest compressibility in the endocardial region, with a progressive decrease towards the epicardium (Fig. 6).
Figure 6.
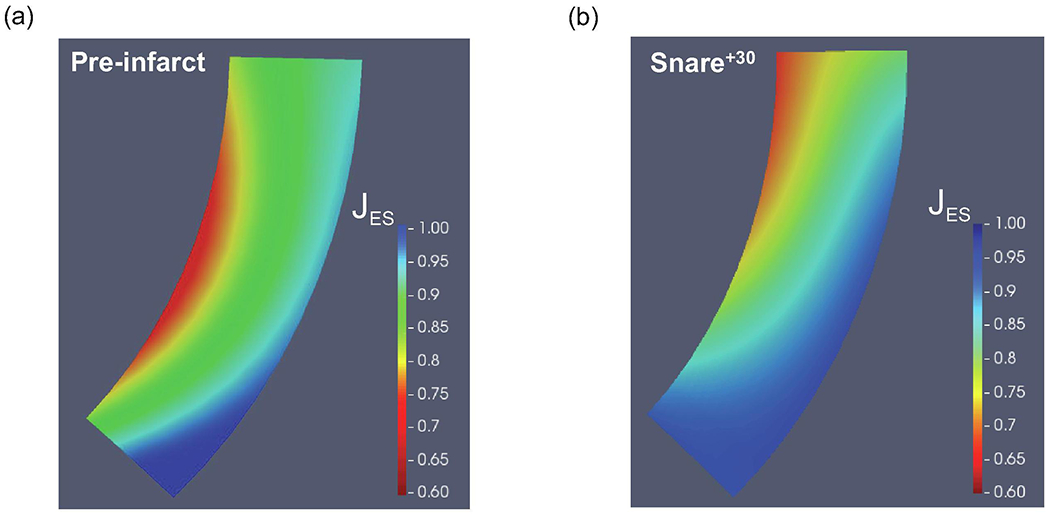
Representative examples of the transmural variation in volume reduction (a) Pre-infarct (T1). (b) Post-infarct (T3).
3.4. Evolution of compressibility following snare: short-term vs. long-term
The regional changes in wall volume at ED following MI were noteworthy (Fig. 7a). The short-term variations in the volume exhibited a nearly monotonic and rapid, significant decrease in the compressibility of the apex within 60 minutes following the snare (Fig. 7a). Similarly, the compressibility of the midwall showed a monotonic decrease, but at a much slower rate (Fig. 7a). In contrast to apical and midwall regions, the base showed an opposite trend by enhancing the compressibility immediately following the snare and maintaining it within the next hour. The further measurements beyond the 60 mins window suggested that altered compressibility of all three regions did not show additional significant variations in the long term, especially up to 12 hours following the snare (Fig. 7b). In particular, the compressibility of the apex and midwall regions seemed to plateau after the variations within the first hour and maintain the changes beyond that point. However, the compressibility of the base region increased moderately beyond the 60 mins window and seemed to plateau afterward.
Figure 7.
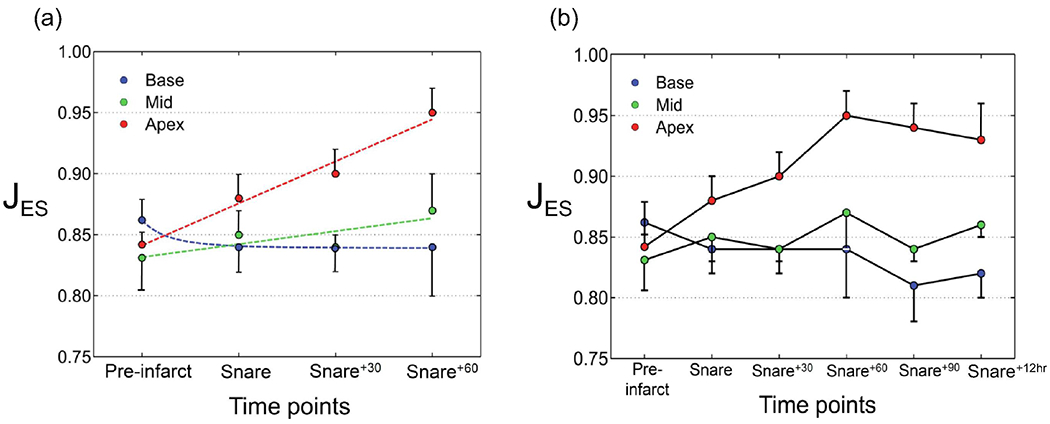
Temporal evolution of average volume changes from pre-infarct to post-infarct for basal, mid, and apical regions. (a) Short-term changes. (b) Long-term changes.
4. Discussion
Accurate understanding of LV kinematics is essential to identifying the fundamental physiological modes of LV function over the cardiac cycle and is particularly sensitive to cardiac disorders such as MI. Two important extant knowledge gaps that we addressed in this study included: (i) a comprehensive understanding of regional and transmural variations in volumetric changes in the normal heart over the cardiac cycle, and (ii) an improved understanding of the alterations in myocardial compressibility following MI. Discussion of specific results is given in the following.
4.1. LV compressibility in normal heart
Overall, we found that local (i.e. in ~ 1 cc volumes) myocardium deformations during the cardiac cycle were significantly non-isochoric, in agreement with multiple previous studies (Table 1). Compressibility was evident in both regional and transmural variations behaviors. Volume reductions increased along the base-to-apex direction, mainly due to the regional differences in contractile strains as well as changes in capillary bed density. Also, the inner portion of the LV free wall exhibited greater compressibility than the outer layer, which could be due in part to direct venous return at endocardial surface. However, the outer layer in the basal region still exhibited about 10-15% volume reduction. This latter finding is of particular interest, as it counters the possibility that the in-vivo sonocrystal measurements are spuriously influenced by artifacts induced by left ventricular trabeculae.
4.2. Comparisons to existing data
To the best of our knowledge the present study is the first detailed, focused report on regional and transmural measurements of in-vivo myocardial compressibility in normal and infarcted hearts. However, several previous studies have also investigated either local (e.g. Villarreal et al., 1991; Waldman et al., 1985) or global (e.g. Judd and Levy, 1991; Zhong et al., 2010) levels of myocardium compressibility. Our measurements of 5-20% reduction in the volume from the basal to apical regions agreed quantitatively well with previous data for normal hearts that were calculated through either measuring difference between arterial inflow and great cardiac venous outflow (Vergroesen et al., 1987; Waldman et al., 1985) or local deformation measurements (Ashikaga et al., 2008; Tsamis et al., 2011, for instance).
As mentioned above, we emphasize the importance of the size of myocardial volume studied. This is because smaller volumes of myocardium tend to contain only a small portion of the capillary network with a limited perfusion capability, leading to only a modest change in the volume under study from ED to Es. In contrast, larger volumes of myocardium likely contain principal branches of coronary arteries, leading to larger changes in volume during the cardiac cycle. In other words, the volume changes are notably heterogeneous inside the myocardium, and their overall values depend on the extent of the volume under study. Lastly, to the best of our knowledge, our measurements of regional and transmural adaptations in compressibility due to MI are reported for the first time here. The opportunity of assessing our post-MI results against comparable data remains to be pursued.
4.3. Temporal and spatial alterations in LV compressibility following MI
The present comprehensive investigation of LV volumetric changes in healthy and infarcted hearts revealed diverse temporal, regional, and transmural adaptations in LVFW volume dynamics due to MI. Time-course calculations of fixed convex hulls engulfing the three regions of the wall enabled us to explore regional differences in the adaptation of LV compressibility. As our MI animal model was designed to consistently produce anteroapical infarct regions, the apical, midwall, and basal regions nearly corresponded to infarct, border, and remote zones, respectively. With this perspective in mind, the infarct zone showed significantly smaller volume reductions during systole, followed by border and remote zones, when compared to the healthy heart. In one of the animals, the infarct zone in the apex even showed volume expansion during systole. The increase of apical volume beyond the ED point was in drastic contrast to normal hearts, where all the regions attained their maximum and minimum volumes around global ED and ES points, respectively. The potential mechanisms for this change are suspected to be impaired contractility and reduced blood supply in the infarct region that prevent myocardium from decreasing its volume during the cardiac cycle. This effect diminishes moving from the infarct (apex) to healthy (basal) region.
4.4. A question of mechanism
The redistribution of blood in the coronary arterial and venous networks during systole has long been thought to be the primary mechanism behind in-vivo myocardial compressibility (Ashikaga et al., 2008; Yin et al., 1996), and may indeed be essential for efficient cardiac energetics. Our measurements of compressibility adaptations in infarcted regions are consistent with the existing knowledge that myocardial perfusion is a key mechanism for myocardial compressibility. That said, we emphasize that our present focus was on ~1 cc volumetric behaviors of myocardium volumetric deformations, and not on more local effects or the elucidation of specific mechanisms. The rationale for this approach was our focus on increasing the accuracy of computational simulations of the heart (see below), as compressibility and its relation to both the specific material model used as well as proper understanding of cardiac kinematics are well known. Therefore, a full investigation of the role of perfusion through measuring regional coronary arterial and venous flows and other potential mechanisms like intrinsic compressibility of myocytes and extracellular matrix must still be addressed.
4.5. Implications in computational modeling and design of cardiac interventions
Although it is common to represent myocardium as an incompressible hyperelastic material in computational modeling of normal and deceased cardiac function, the amount of tissue volume reduction reported in this work suggest that the incorporation of compressibility into myocardium models could play a significant role in the accurate assessment of cardiac function (Hassaballah et al., 2013; Soares et al., 2017). Indeed, if myocardium is modeled as an incompressible material, its tissue volume remains incorrectly constant. Given our observation of volume reductions up to 20%, the frequently used incompressible approximation of myocardium behavior in computational cardiac would likely lead to inaccurate descriptions of LV kinematics that are often used as clinical metrics, particularly an overestimation of wall thickening and an underestimation in long-axis shortening. This is simply due to the fact that incompressible materials have the tendency to laterally bulge when contracting/shortening along the fiber direction, whereas a compressible material is able to undergo considerable shortening without expanding in the cross-fiber direction. Computational models enable the possibility of estimating local in-vivo active forces for a healthy heart and their alterations in response to structural heart disease; however, the accuracy of these estimates becomes substantially dependent on the level of compressibility used in the model, such that incompressible models of myocardium would overestimate the necessary contraction force needed for the heart to maintain the same pressure-volume loop.
4.6. Limitations
Although sonomicrometry offers a high-fidelity approach for measurement of myocardial kinematics and is especially appropriate for time-course studies, it is invasive and requires open chest procedures. It has been speculated that bleeding and slight interstitial swelling from the crystal implantation may affect the accuracy of in-vivo volume measurements. However, using the SPAMM tagging technique, we confirmed the calculations from sonomicrometry with in-vivo strain measurements. We thus believe, to the best of our abilities, that the present measurements represent an accurate representation of local volumetric changes over the cardiac cycle.
5. Concluding Remarks
There has been considerable evidence showing that myocardium is compressible during systole. Detailed quantification of dimensional and kinematic changes due to MI is thus critically important for (i) improving the understanding of the etiology and pathophysiology of post-infarction myocardium remodeling and its impact on organ-level cardiac function, and accordingly, (ii) advancing diagnosis metrics, quantitative risk stratification, therapies, medical device development, and clinical outcomes. We demonstrated evidence of substantial in-vivo systolic compressibility of myocardium, as well as its strong temporal, transmural, and regional variations in normal ovine hearts. Although myocardial compressibility in normal hearts is an important (yet often-neglected) feature by itself, we further demonstrated its significant time-course and regional adaptations following MI to highlight the importance of accounting for this feature in analyzing LV kinematics in health and decease. In the future, and given the data reported in this work, we plan to evaluate the effects of neglecting and accounting for myocardial compressibility on predictive capabilities of cardiac computational modeling.
7. Acknowledgments
This work was supported by the U.S. National Institutes of Health awards K99 HL138288 to RA and R01 HL073021 MSS and RCG.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
6. Conflicts of Interest
None.
8. References
- Allgower EL and Schmidt PH Computing volumes of polyhedra. mathematics of computation, 46(173): 171–174, 1986. [Google Scholar]
- Ashikaga H, Criscione JC, Omens JH, Covell JW, and Ingels NB Transmural left ventricular mechanics underlying torsional recoil during relaxation. American Journal of Physiology-Heart and Circulatory Physiology, 286(2):H640–H647, 2004. doi: 10.1152/ajpheart.00575.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashikaga H, Coppola BA, Yamazaki KG, Villarreal FJ, Omens JH, and Covell JW Changes in regional myocardial volume during the cardiac cycle: implications for transmural blood flow and cardiac structure. American Journal of Physiology-Heart and Circulatory Physiology, 295(2):H610–H618, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axel L and Dougherty L Mr imaging of motion with spatial modulation of magnetization. Radiology, 171(3):841–845, 1989. [DOI] [PubMed] [Google Scholar]
- Gorman III JH, Gupta KB, Streicher JT, Gorman RC, Jackson BM, Ratcliffe MB, Bogen DK, and Edmunds LH Jr Dynamic three-dimensional imaging of the mitral valve and left ventricle by rapid sonomicrometry array localization. The Journal of thoracic and cardiovascular surgery, 112(3):712–724, 1996. [DOI] [PubMed] [Google Scholar]
- Hassaballah AI, Hassan MA, Mardi AN, and Hamdi M An inverse finite element method for determining the tissue compressibility of human left ventricular wall during the cardiac cycle. PloS one, 8(12):e82703, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim E-SH Myocardial tagging by cardiovascular magnetic resonance: evolution of techniques-pulse sequences, analysis algorithms, and applications. Journal of Cardiovascular Magnetic Resonance, 13(1):36, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson BM, Gorman JH, Moainie SL, Guy TS, Narula N, Narula J, John-Sutton MGS, Edmunds LH, and Gorman RC Extension of borderzone myocardium in postinfarction dilated cardiomyopathy. Journal of the American College of Cardiology, 40(6):1160–1167, 2002. [DOI] [PubMed] [Google Scholar]
- Judd RM and Levy BI Effects of barium-induced cardiac contraction on large-and small-vessel intramyocardial blood volume. Circulation research, 68(1):217–225, 1991. [DOI] [PubMed] [Google Scholar]
- May-Newman K, Omens JH, Pavelec RS, and McCulloch AD Three-dimensional transmural mechanical interaction between the coronary vasculature and passive myocardium in the dog. Circulation research, 74(6): 1166–1178, 1994. [DOI] [PubMed] [Google Scholar]
- Mazhari R, Omens JH, Pavelec RS, Covell JW, and McCulloch AD Transmural distribution of three-dimensional systolic strains in stunned myocardium. Circulation, 104 (3):336–341, 2001. doi: 10.1161/01.CIR.104.3.336. [DOI] [PubMed] [Google Scholar]
- McEvoy E, Holzapfel GA, and McGarry P Compressibility and anisotropy of the ventricular myocardium: Experimental analysis and microstructural modeling. Journal of Biomechanical Engineering, 140(8):081004, 2018. [DOI] [PubMed] [Google Scholar]
- Porter WT The influence of the heart-beat on the flow of blood through the walls of the heart. American Journal of Physiology-Legacy Content, 1(2):145–163, 1898. [Google Scholar]
- Preparata FP and Hong SJ Convex hulls of finite sets of points in two and three dimensions. Communications of the ACM, 20(2):87–93, 1977. [Google Scholar]
- Ramanathan T and Skinner H Coronary blood flow. Continuing Education in Anaesthesia, Critical Care & Pain, 5(2):61–64, 2005. [Google Scholar]
- Ratciiffe M, Gupta KB, Streicher JT, Savage EB, Bogen DK, and Edmunds L Use of sonomicrometry and multidimensional scaling to determine the three-dimensional coordinates of multiple cardiac locations: feasibility and initial implementation. IEEE Transactions on Biomedical Engineering, 42(6):587–598, 1995. [DOI] [PubMed] [Google Scholar]
- Richardson WJ and Holmes JW Why is infarct expansion such an elusive therapeutic target? Journal of cardiovascular translational research, 8(7):421–430, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scaramuccius I Theoremata Familiaria Viros Eruditos Consulentia. Apud Joannem Baptistam Bustum, 1695. [Google Scholar]
- Soares JS, Li DS, Lai E, Gorman JH III, Gorman RC, and Sacks MS Modeling of myocardium compressibility and its impact in computational simulations of the healthy and infarcted heart. In International Conference on Functional Imaging and Modeling of the Heart, pages 493–501. Springer, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsamis A, Bothe W, Kvitting J-PE, Swanson JC, Miller DC, and Kuhl E Active contraction of cardiac muscle: In vivo characterization of mechanical activation sequences in the beating heart. Journal of the Mechanical Behavior of Biomedical Materials, 4(7): 1167–1176, 2011. ISSN 1751-6161. doi: https://doi.Org/10.1016/j.jmbbm.2011.03.027. URL http://www.sciencedirect.com/science/article/pii/S1751616111000725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsamis A, Cheng A, Nguyen TC, Langer F, Miller DC, and Kuhl E Kinematics of cardiac growth: In vivo characterization of growth tensors and strains. Journal of the Mechanical Behavior of Biomedical Materials, 8:165–177, 2012a. ISSN 1751-6161. doi: 10.1016/j.jmbbm.2011.12.006. URL http://www.sciencedirect.com/science/article/pii/S1751616111003079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsamis A, Cheng A, Nguyen TC, Langer F, Miller DC, and Kuhl E Kinematics of cardiac growth: in vivo characterization of growth tensors and strains. Journal of the mechanical behavior of biomedical materials, 8:165177, April 2012b. ISSN 1751–6161. doi: 10.1016/j.jmbbm.2011.12.006. URL http://europepmc.org/articles/PMC3298662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergroesen I, Noble M, and Spaan J Intramyocardial blood volume change in first moments of cardiac arrest in anesthetized goats. American Journal of Physiology-Heart and Circulatory Physiology, 253(2):H307–H316, 1987. [DOI] [PubMed] [Google Scholar]
- Villarreal FJ, Lew WY, Waldman LK, and Covell JW Transmural myocardial deformation in the ischemic canine left ventricle. Circulation Research, 68(2):368–381, 1991. doi: 10.1161/01.RES.68.2.368. [DOI] [PubMed] [Google Scholar]
- Wacker CM, Wiesmann F, Bock M, Jakob P, Sandstede JJ, Lehning A, Ertl G, Schad LR, Haase A, and Bauer WR Determination of regional blood volume and intra-extracapillary water exchange in human myocardium using feruglose: first clinical results in patients with coronary artery disease. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 47(5): 1013–1016, 2002. [DOI] [PubMed] [Google Scholar]
- Waldman LK, Fung Y, and Covell JW Transmural myocardial deformation in the canine left ventricle. normal in vivo three-dimensional finite strains. Circulation research, 57(1):152–163, 1985. [DOI] [PubMed] [Google Scholar]
- Yin FC, Chan CC, and Judd RM Compressibility of perfused passive myocardium. American Journal of Physiology-Heart and Circulatory Physiology, 271(5):H1864–H1870, 1996. doi: 10.1152/ajpheart.1996.271.5.H1864. [DOI] [PubMed] [Google Scholar]
- Zhong X, Spottiswoode BS, Meyer CH, Kramer CM, and Epstein FH Imaging three-dimensional myocardial mechanics using navigator-gated volumetric spiral cine dense mri. Magnetic Resonance in Medicine, 64(4):1089–1097, 2010. doi: 10.1002/mrm.22503. [DOI] [PMC free article] [PubMed] [Google Scholar]


