Abstract
Aim:
The total consumption model (TCM) originates from studies of the distribution of alcohol consumption and posits that there is a strong association between the total consumption and the prevalence of excessive/harmful consumption in a population. The policy implication of the TCM is that policy measures which effectively lead to a reduction of the total consumption, will most likely also reduce the extent of harmful consumption and related harms. Problem gambling constitutes a public health issue and more insight into problem gambling at the societal level and a better understanding of how public policies may impact on the harm level, are strongly needed. The aim of this study was to review the literature pertaining to empirical validity of the TCM with regard to gambling behaviour and problem gambling and, on the basis of the literature review, to discuss the policy implications of the TCM.
Methods:
The study is based on a literature mapping through systematic searches in literature databases, and forward and backward reference searches.
Results:
The literature searches identified a total of 12 empirical studies that examined the total consumption model or provided relevant data. All but one of these studies found empirical support for the TCM; that is, a positive association between population gambling mean and prevalence of excessive or problem gambling. Such associations were found both with cross-sectional data and with longitudinal data.
Conclusion:
There is a small but fairly consistent literature lending empirical support to the total consumption model. An important policy implication is that interventions which are successful in reducing overall gambling are likely also to reduce problem gambling incidence.
Keywords: distribution, gambling, gambling policy, literature review, problem gambling
While gambling is a widely enjoyed pastime activity and a source of entertainment for many people, problem gambling and gambling-related harm are also of considerable concern (Korn, Gibbins, & Azmier, 2003). From a public health perspective, it is not only the health and social problems suffered by the small fraction of people who fulfil the criteria for pathological or problem gambling that are of interest, but also the various problems experienced by their family members and others in their social networks, as well as the costs to society at large. Moreover, in this perspective, identification of societal factors that impact on problem gambling incidence are of particular importance, as they imply society’s ability – and even ethical imperative – to prevent new cases. Most research on gambling problems appears to be case centred in the same manner as epidemiological studies of risk factors for various health problems (Rose, 2001), with a focus on distinguishing the relatively few cases from the normal majority. But, if the incidence of gambling problems is closely related to overall gambling in society, as suggested by the total consumption model, our understanding of aetiological factors and potential for problem prevention, should be sought also at the societal level. In this article I review the empirical literature examining the validity of the total consumption model (TCM) with regard to gambling. By way of introduction, I first briefly present the TCM and thereafter discuss how the TCM may be transferred to the area of gambling behaviour.
What is the total consumption model?
The total consumption model (TCM) originates from the alcohol epidemiology field and posits a close relationship between total consumption of alcohol and prevalence of heavy drinkers in a society (Johnstone & Rossow, 2009). In other words, the higher the total consumption, the higher the proportion of heavy drinkers, and vice versa. Given the strong association between heavy drinking and alcohol-related harm, an extension of the model implies an association between total alcohol consumption and incidence of alcohol-related harm (Sulkunen & Warsell, 2012). In the alcohol epidemiology literature, empirical evidence in support of the extended TCM is strong, demonstrating quite systematically that changes in per capita alcohol consumption, which corresponds to total consumption of alcohol in a population, are accompanied by corresponding changes in cause-specific mortality and morbidity, typically associated with harmful use of alcohol (Norström, Hemström, Ramstedt, Rossow, & Skog, 2002; Norström & Ramstedt, 2005).
The validity of the model is of the utmost importance in two respects. From a prevention point of view, it follows from the model that effective measures to reduce the total consumption of alcohol will prevent incidents of alcohol-related harm. With regard to determinants of heavy drinking and alcohol-related harm, the model implies that factors impacting on total consumption will also impact on harm incidence.
In their seminal paper “The population mean predicts the number of deviant individuals” Rose and Day (1990, p. 1031) took the idea of the TCM to a broader and more generic form. They asked: “can the problems of the deviant minority really be understood and managed as though they were independent of the characteristics of the rest of the population?” By analysing data on various types of health-related consumption behaviour and health indicators, Rose and Day (1990) found empirical support for the TCM in four health domains: salt intake, alcohol consumption, blood pressure and body mass index. Thus, they postulated a close relation between total consumption or “the population mean” and the prevalence of excessive consumers or “deviant individuals” similar to the TCM for alcohol consumption, but in more generic terms.
The population mean and the distribution curve
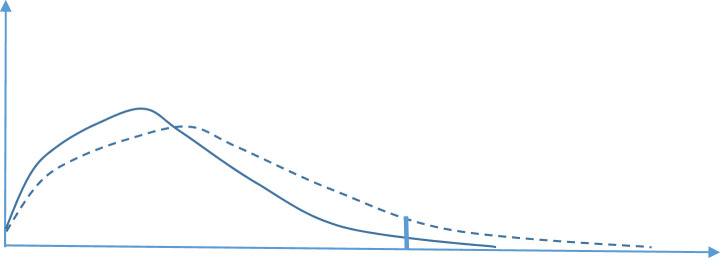
The population mean is a statistical measure of an underlying distribution, which can be described graphically as a curve. The right tail of the distribution represents the “heavy consumers” or the “deviant individuals”. If we consider two populations with different consumption means and fairly similar shaped distribution curves, an upward shift in the mean will necessarily imply an increase in the proportion of excessive consumers, as illustrated in Figure 1. Or, in other words: “The distribution [ … ] moves up and down as a coherent whole: the tail belongs to the body, and the deviants are a part of the population” (Rose & Day, 1990, p. 1033). However, the assumption of fairly similar shaped distribution curves in populations with different means (as illustrated in Figure 1), is not necessarily valid and it is – a priori – not even a prerequisite for the observation of a close relationship between population mean and number of heavy consumers. In principle, we can imagine that, for some reason, the number of heavy consumers varies across populations while the distribution of other consumers is much the same. In that case, the population mean will co-vary with the number of heavy consumers, but variation in population mean does not reflect shifts in the distribution as a whole. Particularly for distributions that are skewed with a long right tail, as is in fact the case for alcohol consumption (Skog, 1985) as well as for gambling (Govoni, 2000; Lund, 2008), the heavy consumers account for a disproportionately large fraction of total consumption (Hansen & Rossow, 2008), implying that the two are bound to co-vary. Some studies of population distributions of alcohol consumption (Rose & Day, 1990; Rossow, Mäkelä, & Kerr, 2014; Skog, 1985), and of salt intake, BMI and blood pressure (Rose & Day, 1990) have, however, taken this point into account and found a positive correlation also between mean among the non-deviant part of the population and prevalence of deviants, thereby suggesting that a shift in population mean reflects a concerted shift in the whole distribution. Another point to consider in this respect is that there are circumstances under which the population mean may change without much change in the proportion of heavy consumers. This may occur when there is a set upper limit to consumption, as was more or less the case under the Swedish alcohol rationing system (Norström, 1987).
Figure 1.
Consumption distribution curves for two samples with different means
Distribution of consumption is shown as proportion of population (Y-axis) by consumption units (X-axis). The distribution curve for Sample 1 (presented with a solid line) has a lower mean than the distribution curve for Sample 2 (presented with a dotted line). The fraction of the population with excessive consumption (consuming above the value marked with a vertical line) is represented by the area under the distribution curve, and this fraction is clearly larger for Sample 2 than for Sample 1.
Does the total consumption model apply to gambling?
As discussed above, the question of whether the total consumption model also applies to gambling behaviour, is of importance regarding our understanding of gambling problem incidence in society as well as the potential for prevention strategies at the societal level. So far, literature searches suggest that no systematic literature mapping has been published on this topic. The aim of this study was therefore to provide such a literature review and, on the basis of this review, to discuss the policy implications of the TCM.
Methods
Literature searches were conducted in MedLine, PsycINFO, and Google Scholar using the search term “gambling” in combination with the terms “total consumption” or “single distribution”, with no restrictions on date of publication, and inclusion only of publications in English. From identified relevant studies, forward and backward searches were also conducted from reference lists and indicated related publications.
Studies were included in the review only when they filled the following criteria: (i) they reported on population or sample mean for a continuous measure of gambling behaviour (e.g., gambling frequency, gambling expenditures) for each of a number of populations or samples, and (ii) they reported on prevalence of “excessive” gambling behaviour (i.e., proportion above a fixed cut-off on the same continuous gambling measure). To allow also for assessing the validity of the extended version of the TCM (i.e., an association between total gambling and prevalence of harm from gambling), an alternative to the second inclusion criterion was applied. This criterion was reported prevalence of problem gambling (i.e., proportion filling criteria for pathological gambling or problem gambling by scoring above a fixed value on a problem gambling instrument, e.g., South Oaks Gambling Screen (SOGS) or Problem Gambling Severity Index (PGSI)).
The TCM can be examined by correlating population means and rates of excessive gambling (as described above) either across a number of populations (cross-sectionally), or within a population over time (longitudinally), or both. Correspondingly, the extended version of the TCM can be examined by correlating population means and rates of problem gambling (as described above) in the same manner. For studies comparing population samples with cross-sectional data (e.g., subsamples from various regions), a minimum of three samples were required, whereas for longitudinal comparison (e.g., survey samples over time within the same country/region) a minimum of two samples was considered sufficient. Thus, studies providing relevant data without explicitly examining the TCM were also eligible for inclusion. However, it is only meaningful to examine empirical validity of the TCM when there is some variation in the population mean. Thus, studies that provided data on population mean and rates of excessive or problem gambling but reported no, or very little, variation in population mean, were not considered relevant in this context.
Results
The literature searches identified altogether 12 studies that met the inclusion criteria. The studies were grouped with respect to whether they provided data for examining the TCM or its extended version, and with respect to type of variation between samples (cross-sectional versus longitudinal). The studies employing cross-sectional data (or some combination of cross-sectional subsamples from two or more surveys over time), mostly had a sufficient number of aggregate units to provide correlation coefficients or some other quantifiable estimate of an association. From these studies, the reported associations between population gambling mean and prevalence of excessive gambling are presented in Table 1, while the corresponding associations with problem gambling (addressing the extended version of the TCM) are presented in Table 2. As can be seen from these tables, all but one study found positive associations, thereby lending support to the TCM and to the extended version of the TCM. Notably, the study in which no association was found (Welte, Barnes, Wieczorek, Tidwell, & Parker, 2002), did not set out to test the TCM, and relatively few respondents in some subsamples led to large standard errors of problem gambling figures.
Table 1.
Studies examining associations between population mean and prevalence of excessive gambling: Cross-sectional design
| First author, year | Country, period | No of samples/ units of analysis | Measure population mean gambling | Measure excessive/ problem gambling | Findings |
|---|---|---|---|---|---|
| Govoni, (2000) | Canada, 1993–1998 | 35 subsamples | Gambling expenditures | Excessive expenditures > 3 000 CAD | r = 0.81 (R2 = 0.66) |
| Expenditures as % of household income | > 15% of household income | r = 0.89 (R2 = 0.80) | |||
| Grun, (2000) | UK, 1993–1994 to 1995–1996 | 2 surveys, 12 regions each | Household gambling expenditures | Expenditures > 20 GBP/week | Regr coeff = 0.8 (1993–1994) 1.6 (1995–1996) |
| Household gambling expenditures | Expenditures > 10% household income | Regr coeff = 0.5 (1993–1994) 1.2 (1995–1996) |
|||
| Hansen, (2008) | Norway, 2002 | Cross-sectional, 73 schools | Gambling frequency | > Total 95% frequency | r = 0.92 |
| Gambling frequency | > weekly gambling | r = 0.90 | |||
| EGM expenditures | > Total 95% expenditures | r = 0.82 | |||
| EGM expenditures | > weekly EGM gambling | r = 0.72 | |||
| Lund, (2008) | Norway, 2002 | 19 counties | Gambling frequency | Frequent gambling | Positive correlation, not quantified |
| Norway, 2004 | 10 subsamples | Gambling frequency | Frequent gambling | Positive correlation, not quantified | |
| Norway, 2005 | 19 counties | Gambling frequency | Frequent gambling | Positive correlation, not quantified |
Notes. CAD = Canadian dollars; GBP = British Pounds; EGM = Electronic Gaming Machines. Govoni (2000) reported the associations as R2, which have been calculated into the correlation coefficient r for the sake of comparison. Grun and McKeigue (2000) reported only regression coefficients, which are reproduced here. All reported estimates of association were statistically significant (p < .05).
Table 2.
Studies examining associations between population mean and prevalence of problem gambling/pathological gambling: Cross-sectional design
| First author, year | Country, period | No of samples/ units of analysis | Measure population mean gambling | Measure problem gambling/ pathological gambling | Findings |
|---|---|---|---|---|---|
| Govoni, (2000) | Canada, 1993–1998 | 35 subsamples | Expenditures | PaG SOGS 5+ | r = 0.91 (R2 = 0.83) |
| Expenditures | PrG SOGS 3–4 | r = 0.81 (R2 = 0.65) | |||
| Exp. as % of income | PaG SOGS 5+ | r = 0.82 (R2 = 0.68) | |||
| Exp. as % of income | PrG SOGS 3–4 | r = 0.84 (R2 = 0.71) | |||
| Welte, (2002) | USA, 1999–2000 | 7 regions | Gambling frequency, gambling losses | PrG DIS 3+ | No apparent correlation, not quantified |
| Abbott, (2006) | Australia, New Zealand, | 9 samples | EGM expenditures | PaG SOGS 5+ | Positive correlation, not quantified |
| Hansen, (2008) | Norway, 2002 | 73 schools | Gambling frequency | LieBet 1+ | r = 0.52 |
| Gambling frequency | DSM 3+ | r = 0.47 | |||
| EGM expenditures | LieBet 1+ | r = 0.33ns | |||
| EGM expenditures | DSM 3+ | r = 0.22 ns | |||
| Markham, (2014) | Australia, 2010 | 62 gambling venues | Gambling expenditures | PGSI 2+ | r = 0.27 |
| Markham, (2016) | Australia, 1999; Canada, 2000; Finland, 2011; Norway, 2002 | 3 subsamples (terciles across country samples) | Gambling losses | Standardised problem gambling score | Positive correlation, not quantified |
| Markham, (2017) | Australia, 1994–2014 | 41 samples | Gambling losses, as % of income | Standardised problem gambling score | Regr coeff = 1.35 |
Notes. PaG = pathological gambling; PrG = problem gambling; SOGS = South Oaks Gambling Screen; DIS = Diagnostic Interview Schedule for gambling; LieBet = Lie/Bet Questionnaire; EGM = Electronic Gaming Machine; DSM = Diagnostic and Statistical Manual of Mental Disorders; PGSI = Problem Gambling Severity Index. Govoni (2000) reported the associations as R2, which have been calculated into the correlation coefficient r, for sake of comparison. Markham et al. (2017) reported only regression coefficient, which is reproduced here. All reported estimates of association, except those marked ns, were statistically significant (p < .05).
A few studies employed longitudinal data only and presented changes in gambling mean and prevalence of excessive – or problem gambling over time (Tables 3 and 4, respectively). Importantly, these studies all examined changes in gambling in relation to some intervention regarding gambling availability. Although no correlation measures were obtained, we can see that changes in mean and excessive – or problem – gambling go in the same direction, thus supporting the above-noted observations from cross-sectional data.
Table 3.
Studies examining associations between population mean and prevalence of excessive gambling: Longitudinal design
| First author, year | Country, period | No of samples/ units of analysis | Measure population mean gambling | Measure excessive gambling | Findings |
|---|---|---|---|---|---|
| Grun, (2000) | UK, 1993–1994 and 1995–1996 | 2 surveys | Household gambling expenditures | Expenditures > 20 GBP/week | Mean expenditures and the two prevalence figures for excessive gambling more than doubled after introduction of national lottery |
| Expenditures > 10% household income | |||||
| Hansen, (2010) | Norway, 2004–2006 | 3 surveys | Gambling frequency | > weekly gambling | Decrease in gambling frequency and EGM expenditure accompanied by decrease in frequent gambling and high expenditures after limited cash flow on EGMs |
| EGM expenditure | 63+ Euros in EGM expenditure |
Note. GBP = British Pounds; EGM = Electronic Gaming Machine.
Table 4.
Studies examining associations between population mean and prevalence of problem gambling: Longitudinal design
| First author, year | Country, period | No of samples/ units of analysis | Measure population mean gambling | Measure excessive/ problem gambling | Findings |
|---|---|---|---|---|---|
| Room, (1999) | Canada, 1996–1997 | 2 surveys | Gambling expenditures and frequency | Short SOGS 2+ and 3+ | Increases in expenditures and frequency and in SOGS 2+ and 3+ after casino opening |
| Lund, (2009) | Norway, 2007 | 2 surveys | Gambling frequency | LieBet 2 | Reduction in both EGM gambling frequency and problem prevalence after EGMs banned |
| Hansen, (2010) | Norway, 2004–2006 | 3 surveys | Gambling frequency and EGM expenditures | SOGS-RA 4+, LieBet 2 | Decrease in gambling frequency and EGM expenditures accompanied by decrease in problem gambling after limited cash flow on EGMs |
Note. SOGS = South Oaks Gambling Screen; LieBet = Lie/Bet Questionnaire; EGM = Electronic Gaming Machine; SOGS-RA = South Oaks Gambling Screen Revised for Adolescents.
As noted in the introduction, the skewed distribution of gambling behaviour, whether in terms of gambling frequency or gambling expenditure, implies that excessive gamblers account for a fairly large fraction of the total amount of gambling, and thus variation in excessive gambling is bound to co-vary with population mean, but not necessarily with gambling behaviour among non-excessive gamblers. The question of whether gambling behaviour, not only at excessive levels but also at medium and lower levels, changes in a concerted manner with a change in population mean, is apparently explored to little extent in the literature. One study from Norway did, however, address this issue, and found, much in line with Skog’s analyses of collectivity in distributions of alcohol consumption, that a change in mean gambling frequency was accompanied by a systematic displacement at all levels of gambling behaviour, and not only at high to excessive levels of gambling (Hansen & Rossow, 2012).
Discussion
Thorough literature searches revealed a fairly modest empirical literature addressing the total consumption model regarding gambling. The findings in these studies were, however, generally consistent in offering empirical support for the validity of the TCM; that is, they found a positive association between population gambling mean and extent of excessive gambling. Correspondingly, the observed positive associations between population gambling and prevalence of problem gambling suggest validity also of the extended version of the TCM. Furthermore, cross-sectional evidence of such co-variation is supported by evidence from longitudinal data, demonstrating concurrent changes in population mean and proportion of excessive or problem gambling. In essence, this fairly consistent literature suggests that the way most people gamble affects those who end up with gambling problems.
In general, it seems the association is stronger when excessive gambling, rather than problem gambling/pathological gambling, is correlated with sample mean. Although there is good evidence that problem gambling (or pathological gambling) is closely related to time and/or amount of money spent on gambling (Markham, Young, & Doran, 2016), there are reasons to expect weaker associations with problem gambling than with some measure of excessive gambling. The fairly low prevalence rates of problem gambling imply some random variation in these rates, both because standard errors of the estimates tend to be relatively large, and also because low prevalent phenomena are more susceptible to measurement errors (Skog, 1992).
The empirical support of the TCM with regard to gambling resembles that from the alcohol epidemiology literature (Norström et al., 2002; Rossow & Norström, 2013; Skog, 1985) and fits into a more general picture of the distribution of health hazards and incidence of health problems in populations (Bramness & Rossow, 2010; Rose, 2001; Rose & Day, 1990; Rossow & Bramness, 2015). In line with Rose (2001; Rose & Day, 1990) and Skog (1985), such regularities in population distributions suggest that factors at the population or aggregate level also impact on the level of excessive consumption and related harm. What these factors are, and how they impact on population gambling and gambling harm, are not well understood. Yet, it seems probable that the mechanisms underlying the observed regularities in gambling behaviour, at least to some extent, resemble those for alcohol consumption (Skog, 1985). Thus, factors at the societal level, including social norms and availability, and the interaction of these factors, likely impact on gamblers at all levels of gambling and thereby on population level and distribution of gambling behaviour. On the other hand, for many games, gambling is not typically a social behaviour, and thus the importance of social interaction is probably of less relevance for collective changes in gambling as compared to alcohol consumption (Skog, 1985).
Given that some aetiological factors operate at the aggregate level, it seems most likely that societies are in a position to intervene and possibly counteract these factors, for instance by controlling availability of gambling. Indeed, the few studies providing longitudinal data in the present review were all from natural experiments, and indicated effects of various forms of gambling availability. In these studies, similar responses to availability interventions were found for both mean gambling behaviour and prevalence of excessive or problem gambling, thereby lending empirical support to the TCM with temporal data. Thus, the TCM has clear implications for policy; strategies that effectively reduce gambling at the population level will likely also reduce excessive gambling and therefore probably reduce problem gambling and related harms. However, there is also another side of this issue. As relatively few problem gamblers account for a disproportionately large fraction of overall gambling and of total gambling revenues, any successful measure to reduce their gambling is likely to reduce the total volume of the trade, both directly and through interactional effects on moderate gamblers. Thus, the gambling industry, as well as governments that depend on gambling revenues for “good causes”, may have good reasons to take a reluctant attitude to implementation of any such measure.
As demonstrated in the present review, the literature on the validity of the total consumption model with regard to gambling is still fairly sparse. Hence, further research on this topic is warranted for several reasons, as noted in the introduction, and this research may take several directions. First, further empirical studies are needed to examine aggregate level associations between population mean on the one hand and excessive gambling as well levels of non-excessive gambling on the other, in line with Skog’s theory of collectivity of consumption (Skog, 1985). Second, there is a need to explore whether consistency in findings from such analyses can be found across various types of games and across various “gambling cultures”. Third, further studies on co-variation between gambling mean and problem gambling rates may well add to and support this literature. However, it should also be kept in mind that variation in problem gambling rates to a significant extent is likely hampered by random error (as discussed above), and findings from such analyses are therefore likely less robust and more mixed, and in turn more difficult to interpret. Last, but not least, studies identifying factors at the societal level that impact on collective changes in gambling behaviour are urgently needed, as well as evaluations of whether and how various prevention measures may impact on both the way most people gamble and those most vulnerable to gambling problems.
Acknowledgements
Two anonymous reviewers provided helpful comments on a previous version of this manuscript.
Footnotes
Declaration of conflicting interests: The author declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Norwegian Institute of Public Health.
References
- Abbott M. (2006). Do EGMs and problem gambling go together like a horse and carriage? Gambling Research, 18(1), 7–38. [Google Scholar]
- Bramness J. G., Rossow I. (2010). Can the total consumption of a medicinal drug be used as an indicator of excessive use? The case of carisoprodol. Drugs: Education, Prevention, and Policy, 17(2), 168–180. doi:10.3109/09687630903264278 [Google Scholar]
- Govoni R. J. (2000). Gambling behaviour and the distribution of alcohol consumption model (PhD thesis). University of Windsor, Canada: Retrieved from https://scholar.uwindsor.ca/etd/2186 [Google Scholar]
- Grun L., McKeigue P. (2000). Prevalence of excessive gambling before and after introduction of a national lottery in the United Kingdom: Another example of the single distribution theory. Addiction, 95(6), 959–966. doi:10.1046/j.1360-0443.2000.95695912.x [DOI] [PubMed] [Google Scholar]
- Hansen M. B., Rossow I. (2008). Adolescent gambling and problem gambling: Does the total consumption model apply? Journal of Gambling Studies, 24(2), 135–149. doi:10.1007/s10899-007-9082-4 [DOI] [PubMed] [Google Scholar]
- Hansen M. B., Rossow I. (2010). Limited cash flow on slot machines: Effects of prohibition of note acceptors on adolescent gambling behaviour. International Journal of Mental Health and Addiction, 8(1), 70–81. doi:10.1007/s11469-009-9196-2 [Google Scholar]
- Hansen M. B., Rossow I. (2012). Does a reduction in the overall amount of gambling imply a reduction at all levels of gambling? Addiction Research & Theory, 20(2), 145–152. [Google Scholar]
- Johnstone B. M., Rossow I. (2009). Prevention of alcohol related harm: The total consumption model In Krantzler H. R., Korsmeyer P. (Eds.), Encyclopedia of drugs, alcohol and addictive behavior (3rd ed, Vol. 4, pp. 89–92). Detroit, MI: Macmillan Publishing. [Google Scholar]
- Korn D., Gibbins R., Azmier J. (2003). Framing public policy towards a public health paradigm for gambling. Journal of Gambling Studies, 19(2), 235–256. doi:10.1023/a:1023685416816 [DOI] [PubMed] [Google Scholar]
- Lund I. (2008). The population mean and the proportion of frequent gamblers: Is the theory of total consumption valid for gambling? Journal of Gambling Studies, 24(2), 247–256. doi:10.1007/s10899-007-9081-5 [DOI] [PubMed] [Google Scholar]
- Lund I. (2009). Gambling behaviour and the prevalence of gambling problems in adult EGM gamblers when EGMs are banned: A natural experiment. Journal of Gambling Studies, 25, 215–225. [DOI] [PubMed] [Google Scholar]
- Markham F., Young M., Doran B. (2014). Gambling expenditure predicts harm: Evidence from a venue-level study. Addiction, 109(9), 1509–1516. [DOI] [PubMed] [Google Scholar]
- Markham F., Young M., Doran B. (2016). The relationship between player losses and gambling-related harm: Evidence from nationally representative cross-sectional surveys in four countries. Addiction, 111, 320–330. [DOI] [PubMed] [Google Scholar]
- Markham F., Young M., Doran B., Sugden M. (2017). A meta-regression analysis of 41 Australian problem gambling prevalence estimates and their relationship to total spending on electronic gaming machines. BMC public health, 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norström T. (1987). The abolition of the Swedish alcohol rationing system: Effects on consumption distribution and cirrhosis mortality. British Journal of Addiction, 82, 633–641. [DOI] [PubMed] [Google Scholar]
- Norström T., Hemström Ö., Ramstedt M., Rossow I., Skog O.-J. (2002). Mortality and population drinking In Norström T. (Ed.), Alcohol in postwar Europe: Consumption, drinking patterns, consequences and policy responses in 15 European countries (pp. 157–175). Stockholm, Sweden: National Institute of Public Health. [Google Scholar]
- Norström T., Ramstedt M. (2005). Mortality and population drinking: A review of the literature. Drug and Alcohol Review, 24(6), 537–547. doi:10.1080/09595230500293845 [DOI] [PubMed] [Google Scholar]
- Room R., Turner N. E., Ialomiteanu A. (1999). Community effects of the opening of the Niagara casino. Addiction, 94(10), 1449–1466. doi:10.1046/j.1360-0443.1999.941014492.x [DOI] [PubMed] [Google Scholar]
- Rose G. (2001). Sick individuals and sick populations. International Journal of Epidemiology, 30(3), 427–432. doi:10.1093/ije/30.3.427 [DOI] [PubMed] [Google Scholar]
- Rose G., Day S. (1990). The population mean predicts the number of deviant individuals. BMJ, 301, 1031–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossow I., Bramness J. G. (2015). The total sale of prescription drugs with an abuse potential predicts the number of excessive users: A national prescription database study. BMC Public Health, 15, 288 doi:10.1186/s12889-015-1615-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossow I., Mäkelä P., Kerr W. (2014). The collectivity of changes in alcohol consumption revisited. Addiction, 109(9), 1447–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossow I., Norström T. (2013). The use of epidemiology in alcohol research. Addiction, 108(1), 20–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skog O.-J. (1985). The collectivity of drinking cultures: A theory of the distribution of alcohol consumption. British Journal of Addiction, 80, 83–99. [DOI] [PubMed] [Google Scholar]
- Skog O.-J. (1992). The validity of self-reported drug use. British Journal of Addiction, 87(4), 539–548. [DOI] [PubMed] [Google Scholar]
- Sulkunen P., Warsell L. (2012). Universalism against particularism: Kettil Bruun and the ideological background of the total consumption model. Nordic Studies on Alcohol and Drugs, 29(3), 217–232. [Google Scholar]
- Welte J. W., Barnes G. M., Wieczorek W. F., Tidwell M.-C., Parker J. (2002). Gambling participation in the U.S.: Results from a national survey. Journal of Gambling Studies, 18(4), 313–337. [DOI] [PubMed] [Google Scholar]