Spatio-temporal estimation of the daily cases of COVID-19 in worldwide using random forest machine learning algorithm

Highlights

• •Daily number of COVID-19 cases was estimated by the random forest method.
• •Case estimates by random forest were mapped and compared to actual data.
• •Random forest performed well in estimating the number of cases in the near future.

Abstract

Novel Coronavirus pandemic, which negatively affected public health in social, psychological and economical terms, spread to the whole world in a short period of 6 months. However, the rate of increase in cases was not equal for every country. The measures implemented by the countries changed the daily spreading speed of the disease. This was determined by changes in the number of daily cases. In this study, the performance of the Random Forest (RF) machine learning algorithm was investigated in estimating the near future case numbers for 190 countries in the world and it is mapped in comparison with actual confirmed cases results. The number of confirmed cases between 23/01/2020 - 17/06/2020 were divided into 3 main sub-datasets: training sub-data, testing sub-data (interpolation data) and estimating sub-data (extrapolation data) for the random forest model. At the end of the study, it has been found that R² values for testing sub-data of RF model estimates range between 0.843 and 0.995 (average R²= 0.959), and RMSE values between 141.76 and 526.18 (mean RMSE = 259.38); and that R² values for estimating sub-data range between 0.690 and 0.968 (mean R² = 0.914), and RMSE values between 549.73 and 2500.79 (mean RMSE = 909.37). These results show that the random forest machine learning algorithm performs well in estimating the number of cases for the near future in case of an epidemic like Novel Coronavirus, which outbreaks suddenly and spreads rapidly.

1. Introduction

Novel Coronavirus disease 2019 (COVID-19), which first appeared in Wuhan, China in December 2019, has caused the death of more than 450 thousand people worldwide as of June 2020 [1]. In addition, COVID-19 quickly became a worldwide epidemic due to its high contagiousness and rapid spread [2]. For this reason, all countries take steps to prevent the spread of the COVID-19 outbreak. Many medical studies have been conducted to examine and treat the disease caused by this new type of virus in recent months [3], [4], [5], [6], [7]. In addition, many studies have been conducted to examine the social, psychological and economic effects of the COVID-19 outbreak and the changes it causes [8], [9], [10], [11], [12], [13]. Epidemiological, statistical and mathematical models have also been introduced to predict the distribution, to observe the changes depending on meteorological conditions, and to examine the structure of this epidemic which affects all countries globally [14], [15], [16], [17], [18], [19], [20], [21]. Besides, the performance of machine learning approaches for the diagnosis and treatment of the disease was also studied [22], [23], [24], [25], [26], [27], [28]. All these studies reveal the general structure of such an epidemic and disease that humanity has not encountered before and its effects on society. For this reason, it is very important to research each individual and social impact that occurs in the COVID-19 pandemic, in different disciplines with different methods, along with its causes. This idea has been the main motivation for this study. In this study, the performance of the Random Forest (RF) method, which is a machine learning algorithm, was analyzed in estimating the daily increase rates and the number of daily cases in the near future and synchronous parallel computing was carried out for 190 countries.

In recent years, machine learning algorithms and artificial intelligence approaches have been used successfully in many different fields [29], [30], [31], [32], [33], [34], [35], [36]. One of the most important of these algorithms is Random forest machine learning [37], [37]. This method occurs with the combination of many specialized decision trees. The input-output relationship is learned by the machine in certain confidence intervals with the help of experimental data. The success level of the estimation model is determined by testing validation data after sufficient learning is provided by the machine.

The main purpose of this study is to discover the spread estimation of the daily cases of the COVID-19 outbreak for the near future using RF machine learning algorithm. Thus, by using the daily changes in the number of confirmed cases for 190 countries worldwide, the spatio-temporal distribution of the outbreak in the world is estimated and mapped. In addition, this study also aims to reveal the performance of the RF algorithm both in determining the spread of the outbreak and in estimating cases for the near future.

2. Materials and methods

2.1. The data repository and software resources

The COVID-19 data repository1 used in the study was obtained from the Johns Hopkins University Center for Systems Science and Engineering (JHU CSSE) [39]. In this study, the number of updated and confirmed cases for 147 days between 23/01/2020 – 17/06/2020 in 190 countries worldwide was used. The entire study was conducted in the R programming environment [40], [41] and Random Forest [42] was used for random forest calculations, covid19.analytics [43] for COVID-19 data, rnaturalearth [44] for mapping, ggpot2 [45] for visualizing of data, and caret [46] R packages for data preparation and separation.

2.2. Random forest

The random forest approach proposed by Breiman [37] is a machine learning algorithm with many decision trees. It is a combination of Bagging [47] and Random Subspaces [48] methods. This method has proved its success in both regression and classification problems in recent years and is one of the best machine learning algorithms used in many different fields [25], [30], [34], [38], [49], [50], [51]. In RF algorithm, firstly, data set is randomly divided into two parts as training data (the in-Bag) for learning and validation data (the-out of bag) for testing the learning level. 2/3 of the data set is devoted to training data and 1/3 to validation data. Later, many decision trees are randomly created with “boot-strap samples” from the data set. The branching of each tree is determined by randomly selected predictors at node points. The RF Final estimate is the average of all results from each tree. Therefore, each individual tree affects RF estimation at certain weights. Since this method shows “black box” feature, each tree is not examined individually [52]. RF algorithm is stronger than other machine learning algorithms due to its ability to randomly receive training data from subsets and form trees with random algorithm [53]. In addition, the random forest algorithm maintains the overfitting level as training is carried out on randomly selected different sub-datasets by boot-strap sampling.

2.3. Process steps

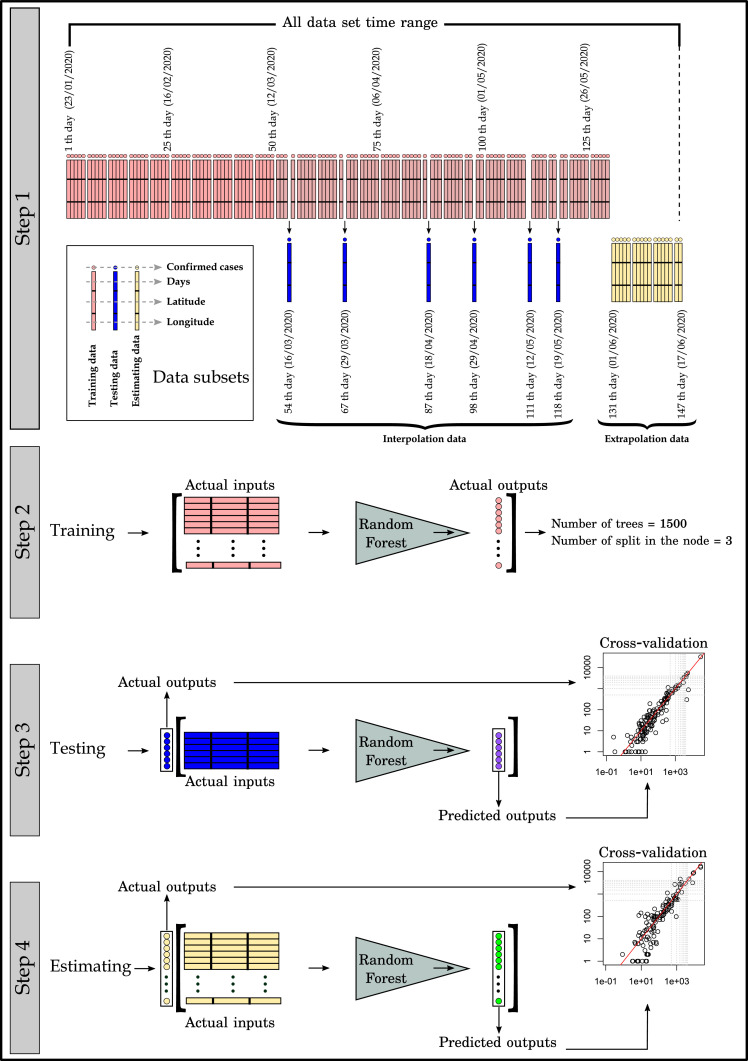
This study was carried out in 4 main stages. These process steps are shown in Fig. 1 and explained below.

Fig. 1.

Process steps in this study.

1. Step, data split process; the number of confirmed cases for 190 countries between 23/01/2020 – 17/06/2020 is divided into 3 main sub-datasets. The first data set is the training sub-dataset between 23/01/2020–31/05/2020. The second sub-dataset is the testing sub-dataset consisting of 6 days (16–29 March, 18–29 April and 12–19 May) data randomly selected from the training data set days after the 50th day and separated from the training data set. This data set is different from validation data, which is inside the RF algorithm system and whose data is separated as 1/3. The third sub-dataset is the estimating sub-dataset, where future predictions are made for the date range 01/06/2020 - 17/06/2020. This data set is separated from training data like the testing data set and is not included in the RF learning algorithm. Testing sub-data shows randomly selected days (after the 50th day) among the date ranges in the training data set (Interpolation), while estimating sub-data shows data from the days (near future) after the end of the training data (Extrapolation).

2. Step, RF training process; machine learning process is performed at this stage by applying RF algorithm with training data. In this process, determining the number of trees to be created and the number of splits at the node points of the trees is important for accurate predictions. 1/3 validation sub-datasets created in RF algorithm were used for the optimization of these values. At the end of the optimization, the number of trees was found as 1500 for the most suitable model and the number of splits on the nodes as 3 (Average R² = 0.952 at 10–fold cross-validation, average RMSE = 354.74).

3. Step, RF testing process; after performing RF training with actual data, the model created is tested with the testing sub-dataset separated from the data set and the results are shown in the cross-validation diagram. The performance of the model is determined by mean error (ME, Eq. (1)), root mean square error (RMSE, Eq. (2)) and the correlation coefficient (R², Eq. (3)).

$$ME=\frac{1}{n}\sum _{i=1}^n(A_i-P_i)$$ (1)

$$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n{(A_i-P_i)}^2}$$ (2)

$$R^2=\left(1-\frac{\sum _{i=1}^n{\left(A_i-P_i\right)}^2}{\sum _{i=1}^n{\left(A_i-\overline{A}\right)}^2}\right)$$ (3)

where n is the total number of points in cross-validation, P_i, A_i and $\overline{A}$ are the estimated values, actual values and average of actual values, respectively.

4. Step, RF estimating process; Estimates of confirmed cases in estimating sub-dataset are performed with RF model and results are shown in cross validation diagram. In this process, 17-day estimates of COVID-19 cases for the near future were calculated with RF algorithm. The results were interpreted with the performance descriptors used in Step 3.

3. Results and discussion

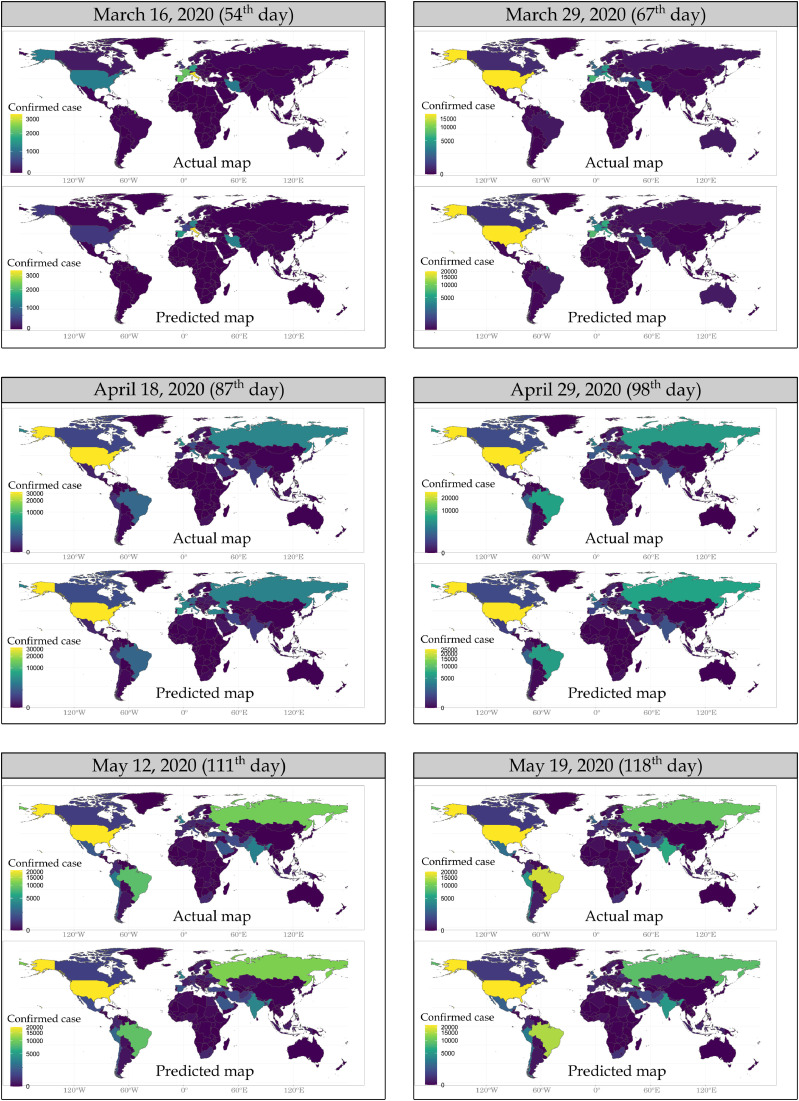
Fig. 2 shows the distribution maps of actual confirmed daily case numbers in 190 countries worldwide for testing data and the distribution maps of daily case numbers estimated by RF model for the same day in comparison. These maps were created with the actual and estimated values of the randomly selected and separated test data from the training data set for the days after the 50th day, as stated earlier. Estimates of the number of cases by RF model were found very close to the number of actual confirmed cases for all countries except the USA, France and Spain on March 16, 2020 (54th day). It is thought that the most important reason why RF estimation results are not correct for these three countries, which are among the countries most affected by the COVID-19 outbreak is due to the sudden increase in the spread of the epidemic in mid-March [1]. RF map of daily case estimates seems to be quite similar to the actual data on March 29, 2020 (67th day) except Turkey. The rapid increase in the number of cases in late March and early April in Turkey is slightly faster than the level estimated by the model. A similar situation can be seen in Saudi Arabia on April 18, 2020 (87th day). Also, when the maps of the 87th day are compared, it is seen that there are fewer daily cases in France and Spain than RF estimation. It is remarkable that there is a very high similarity between the actual daily number of cases and the number of cases estimated by the RF model, especially on the maps of 29 April 2020 (98th day), 12 May 2020 (111th day) and 19 May 2020 (118th day). Thus, it is clearly seen in the comparative maps, especially after the 90th day, that the model suggests closer estimates to actual data.

Fig. 2.

For the testing data, comparative maps of daily cases estimated using the RF model with actual confirmed cases.

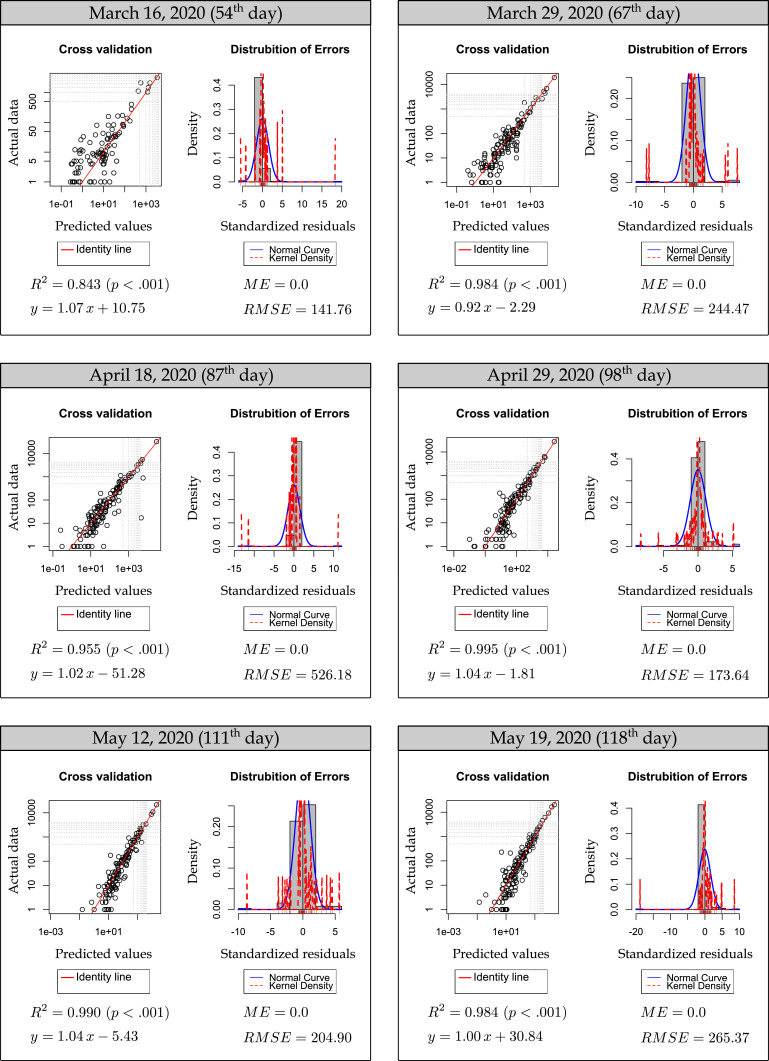
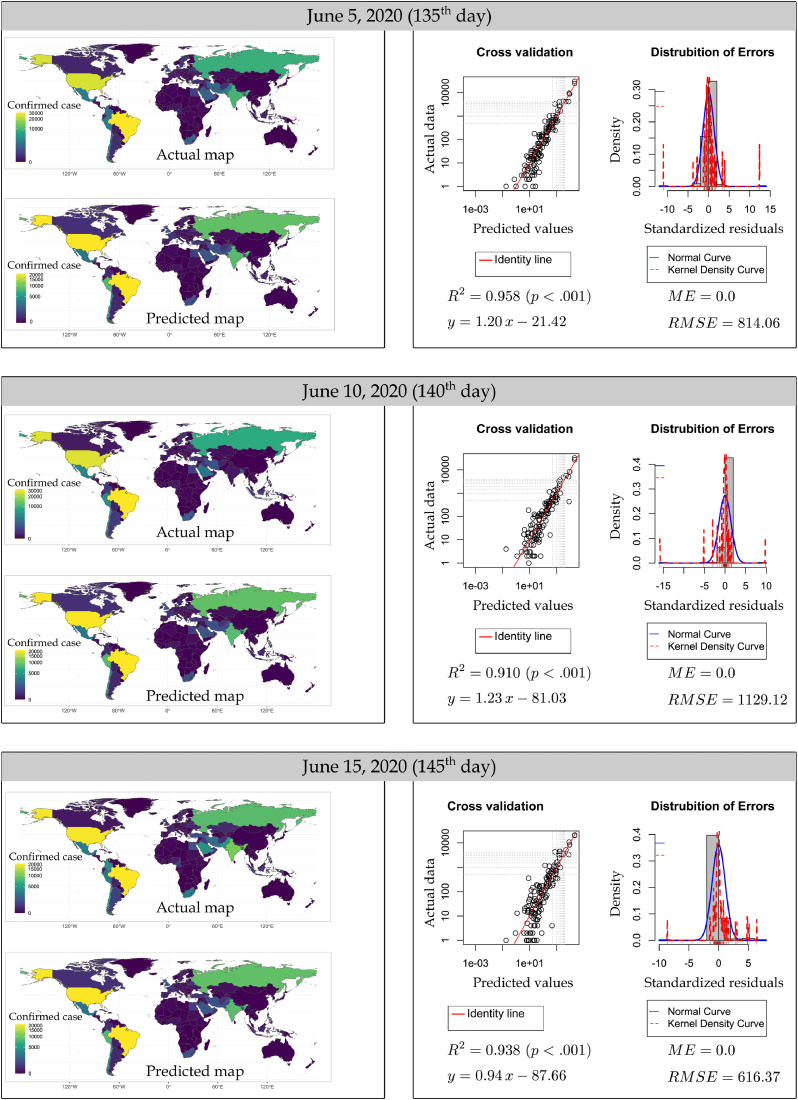
Fig. 3 shows the distribution of errors and the cross-validation diagrams, where actual numbers and RF estimates are given together for the testing subset. Accordingly, R² has been calculated as 0.843, 0.984, 0.955, 0.995, 0.990 and 0.984, RMSE as 141.76, 244.47, 526.18, 173.64, 204.90, and 265.37 for the 54th, 67th, 87th, 98th, 111th and 118th days, respectively. As shown in the distribution of the errors graph, ME values were determined as 0.0 on all days tested. It is seen that most of the standardized errors (except a few outlier) in all diagrams are concentrated at the 0.0 point and the error distributions fit the normal distribution. These results reveal the success of the random forest algorithm in estimating the number of missing COVID-19 daily cases in the training data time range. Fig. 4 shows diagrams that demonstrate estimation performance of the RF model for the near future. In these diagrams, the actual confirmed cases and RF estimation results of 3 days (5–10–15 June 2020) selected from estimation data, which have never been introduced to the machine as training data interval, are shown in both maps and cross validation diagrams comparatively. Accordingly, R² has been calculated as 0.958, 0.910 and 0.938; and RMSE as 814.06, 1129.12 and 616.37 for 135th, 140th and 145th days, respectively. In addition, Table 1 lists the performance identifiers between actual confirmed cases and RF model estimation values for each day from June 1 to 17, 2020. According to this table, the best RF model estimation for the near future has been calculated as the highest R² 0.968 and the lowest RMSE 549.73 for the 6 June 2020 data. In addition, the average R² value for 17 days between 1 and 17 June 2020 has been found as 0.914 and the average RMSE value has been found as 909.37. These results show the success of the RF machine learning algorithm in estimating the number of COVID-19 daily cases in the near future. However, when Table 1 is analyzed, it is seen that there is a significant decrease in RF estimation performance for June 17, 2020. The main reason for this is thought to be the unpredictably high increase in the number of daily cases (36,179) recorded in Chile that day. RF model estimation maps and cross-validation diagrams for 1–17 June 2020 are presented in Figure S1 in the Supplementary Material.

Fig. 3.

Cross-validation and error distribution diagrams for the testing data.

Fig. 4.

For 3 days (5-10-15 June 2020) selected from the estimating data, comparative maps of daily cases estimated using the RF model with actual confirmed cases.

Table 1.

The performance identifiers between actual confirmed cases and RF model estimation values for each day from June 1 to 17, 2020.

Date	Day	R2	RMSE	Linear regression equation
01 June 2020	131 th	0.916	802.76	$y=0.77x+57.94$
02 June 2020	132 th	0.915	820.23	$y=1.06x-30.37$
03 June 2020	133 th	0.959	632.60	$y=1.10x+30.62$
04 June 2020	134 th	0.942	802.60	$y=1.15x+1.56$
05 June 2020	135 th	0.958	814.06	$y=1.20x-21.42$
06 June 2020	136 th	0.968	549.73	$y=1.11x+13.17$
07 June 2020	137 th	0.955	575.82	$y=0.88x+67.55$
08 June 2020	138 th	0.940	722.57	$y=0.78x+76.37$
09 June 2020	139 th	0.825	1136.91	$y=0.99x+23.80$
10 June 2020	140 th	0.910	1129.12	$y=1.23x-81.03$
11 June 2020	141 th	0.955	815.86	$y=1.19x+18.52$
12 June 2020	142 th	0.930	830.80	$y=1.13x+10.36$
13 June 2020	143 th	0.957	627.43	$y=1.09x+59.90$
14 June 2020	144 th	0.855	967.45	$y=0.92x+153.64$
15 June 2020	145 th	0.938	616.37	$y=0.94x-87.66$
16 June 2020	146 th	0.929	1114.14	$y=1.28x-20.81$
17 June 2020	147 th	0.690	2500.79	$y=1.38x+105.53$
Mean		0.914	909.37

When the results of the study are evaluated in general, it has been shown that the random forest machine learning algorithm can create appropriate estimations in determining the number of near future cases in a sudden emerging epidemic. It is thought that appropriate estimations can be made for the distant future as well by increasing the input data and introducing other factors affecting the epidemic as an appropriate parameter to the random forest learning algorithm. Based on these results, a hybrid approach can be created by using the advantages of other machine learning algorithms in future studies. Spatio-temporal spread rate estimation of a sudden epidemic and potentially risky areas identification might also be possible with the aforementioned approach.

4. Conclusions

In this study, the performance of the random forest machine learning algorithm in estimating near future COVID-19 confirmed cases were investigated. In addition, RF estimation results were calculated and evaluated separately for both randomly selected days from the training data and for the days outside the training data. The comparative results are shown in cross-validation diagrams as well as distribution maps created for 190 countries. R² values of RF model estimations calculated for 6 days randomly selected among training data set time intervals were found to range between 0.843 and 0.995, and RMSE values between 141.76 and 526.18. In addition, according to the performance indicators of the RF model estimation results for the near future for the date range of 1–17 June 2020, which are out of the training data set time interval, the R² values vary between 0.690 and 0.968, the average is 0.914 and the RMSE values vary between 549.73 and 2500.79 and the average is 909.37. These results show that the random forest machine learning algorithm has produced very successful results in estimating the number of cases for the near future in case of a sudden epidemic. This study can be improved by increasing the number of input variables (number of daily tests, the population of the country, number of quarantined people, number of people recovering, meteorological data, measures taken by countries etc.) affecting the daily increase in cases and by using different machine learning algorithms in a hybrid way. However, it should be noted that the machine learning process and the estimation periods will be longer in this case. These issues should be taken into consideration for future studies.

CRediT authorship contribution statement

Cafer Mert Yeşilkanat: Investigation, Data curation, Writing - original draft, Visualization, Conceptualization, Methodology, Software, Formal analysis, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. All work was conducted by Cafer Mert Yeşilkanat