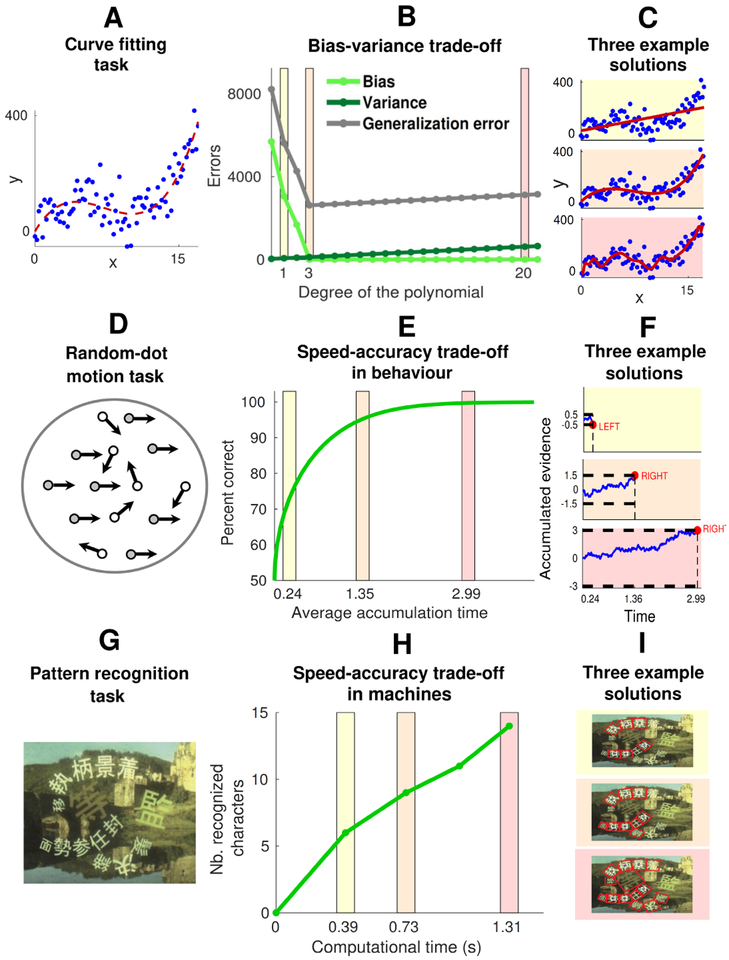
Figure 1: Trade-offs in inference with limited information, time, and computational resources.

Top panels: The bias-variance trade-off. A A curve-fitting task that requires an inference about the hidden curve (red dashed line) that is most likely to generate the data points (blue dots) with Gaussian noise [29, 30]. B Under limited data, increasing the degree of the fitting polynomial (and hence the statistical complexity of the solution) decreases errors due to bias (underfitting) but increases errors due to variance (overfitting). The total generalization error is minimized at intermediate complexity. C Three example solutions of increasing statistical complexity (yellow to pink); intermediate is optimal in this case. Middle panels: An example of speed-accuracy trade-off in behaviour. D A random-dot motion task that requires an inference about the dominant direction of motion of stochastic visual dots [31]. E The percentage of correct responses can be increased by increasing the time to sequentially process information (accumulation time) about the direction of motion of the dots. F Example solutions showing increased accuracy but longer decision times as the pre-defined bound on the total evidence to integrate in the decision process (black dashed line) increases (yellow to pink). Bottom panels: An example of speed-accuracy trade-off in machines (adapted from [32]). G A pattern-recognition task that requires the identification of characters embedded in a scene image. H This task can be solved by an “anytime” algorithm that is governed by a trade-off between accuracy and computational time to process information in the image. I As the running time increases, the algorithm localizes (red rectangles) more and more characters (yellow to pink).