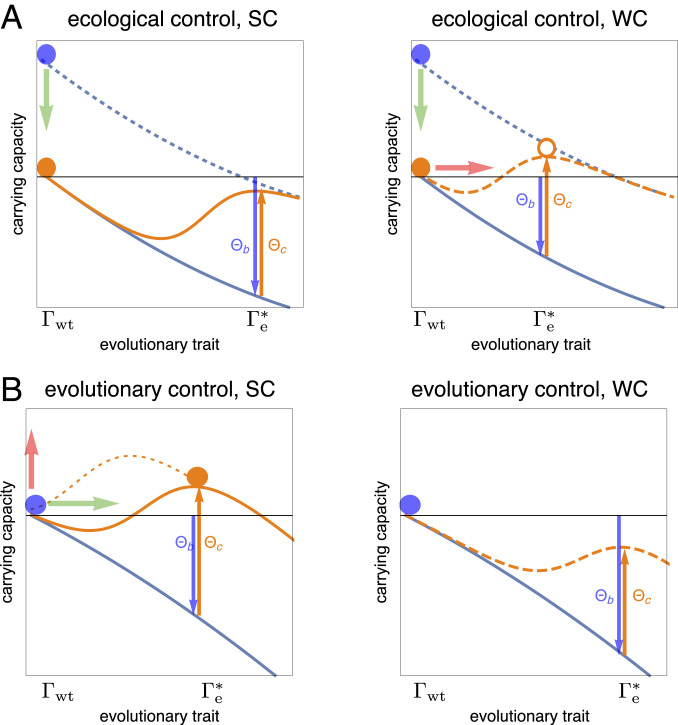
Fig. 1.

Modes and leverage of eco-evolutionary control. A pathogen population with mean trait $\mathrm{\Gamma }$ under control with amplitude $\zeta$ lives in a free fitness landscape ${\psi }_p\left(\mathrm{\Gamma },\zeta \right)$ (orange lines), which is the sum of a background component ${\psi }_b\left(\mathrm{\Gamma }\right)$ (blue lines) and a control landscape $f_c\left(\mathrm{\Gamma },\zeta \right)$. An evolutionary path from the wild type ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ to an optimal evolved state ${\mathrm{\Gamma }}_e*$ involves the control leverage ${\mathrm{\Theta }}_c=2N_p^e\left[f_c\left({\mathrm{\Gamma }}_e*,\zeta \right)-f_c\left({\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}},\zeta \right)\right]$ (orange arrows) and a change in background free fitness, ${\mathrm{\Theta }}_b={\psi }_b\left({\mathrm{\Gamma }}_e*\right)-{\psi }_b\left({\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}\right)$ (blue arrows). (A) Ecological control, starting from an uncontrolled wild-type pathogen (blue dots), has the objective of reducing the pathogen’s carrying capacity (green arrows)—here by antibody binding—and the collateral effect of resistance evolution (red arrows). SC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b<0$) suppresses the evolution of resistance and generates a stable wild type (orange dot; i.e., the reverse path from ${\mathrm{\Gamma }}_e*$ to ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ fulfils the minimum-leverage condition [5]). WC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b>0$) triggers the evolution of resistance (orange circle). (B) Evolutionary control has the objective of eliciting a new pathogen trait (green arrow) and the collateral of increasing its carrying capacity (red arrow). Dynamical control elicits the evolved trait along a path of positively selected trait increments, which requires elevated transient control amplitudes (dotted orange line). SC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b>0$) generates a stable evolved trait (orange dot; i.e., the path from ${\mathrm{\Gamma }}_{\mathrm{w}\mathrm{t}}$ to ${\mathrm{\Gamma }}_e*$ fulfils the minimum-leverage condition [5]). WC (${\mathrm{\Theta }}_c+{\mathrm{\Theta }}_b<0$) cannot elicit an evolved state (or triggers a reversal to the wild type).