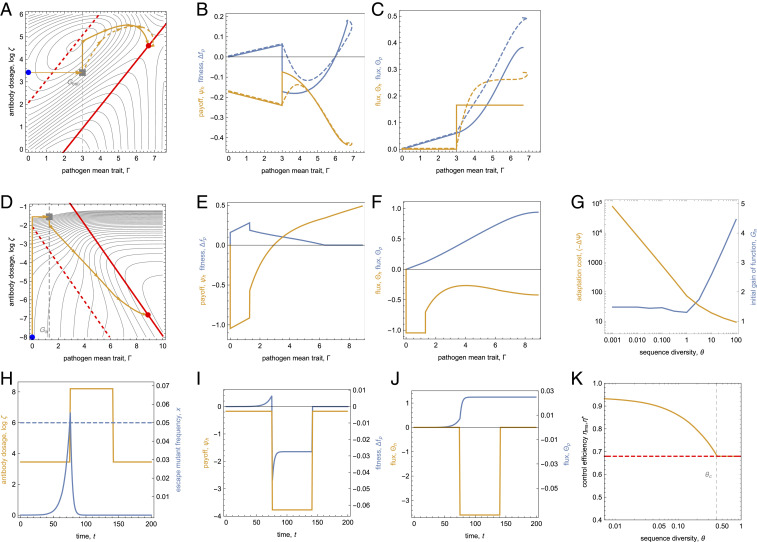
Fig. 4.

Control dynamics. (A–C) Ecological control by instantaneous-update protocols. (A) Control paths $\left(\mathbf{\Gamma },\mathit{\zeta }\right)$ generated by local deterministic (dashed orange) and greedy (solid orange) control dynamics. These paths start with a pathogen escape mutation (gray square) and converge to the optimal stationary protocol $\left(\mathrm{\Gamma }*,\zeta *\right)$ (red dot), which is a computational and a Nash equilibrium. (B) Time-dependent pathogen fitness, $f_p\left(t\right)$, and host payoff, ${\psi }_h\left(t\right)$, of these control paths. (C) Pathogen flux, ${\mathrm{\Theta }}_p\left(t\right)$, and host flux, ${\mathrm{\Theta }}_h\left(t\right)$. Both fluxes are monotonically increasing functions of the path coordinate $\mathrm{\Gamma }\left(t\right)$. (D–G) Evolutionary control for adaptive trait formation. (D) Deterministic computational control path in the SC regime (orange line). This path maximizes the score $\mathrm{\Omega }\left(\mathit{\Gamma },\mathit{\zeta }\right)$ for given values of the speed parameter and of the pathogen sequence diversity (here $\lambda =0$, $\theta =1$) (SI Appendix, Fig. S3). The initiation phase ($\mathrm{\Gamma }\le G_{\mathrm{i}\mathrm{n}}$) with a gain-of-function mutation (gray square) is followed by a breeding phase ($\mathrm{\Gamma }>G_{\mathrm{i}\mathrm{n}}$); the path converges to the optimal stationary protocol (red dot), which is a computational but not a Nash equilibrium. (E) Pathogen fitness, $f_p\left(t\right)$, and host payoff, ${\psi }_h\left(t\right)$, along the computational control path. (F) Fluxes ${\mathrm{\Theta }}_p\left(t\right)$ and ${\mathrm{\Theta }}_h\left(t\right)$ as functions of the path coordinate $\mathrm{\Gamma }\left(t\right)$. This path has negative increments of the host flux ($\partial \mathrm{\Theta }/\partial \mathrm{\Gamma }<0$) at the start and in the final segment. (G) Cost of adaptation, $\left(-\mathrm{\Delta }\mathrm{\Omega }\right)$ (orange), and initial gain-of-function trait, $G_{in}$ (blue), of the maximum-score computational protocol as a function of the pathogen diversity, $\theta$ for $\lambda =0$. (H–K) Metastable ecological control. (H) Time-dependent protocol $\zeta \left(t\right)$ with baseline dosage ${\zeta }_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$, boost dosage ${\zeta }_{\mathrm{r}\mathrm{e}\mathrm{s}}$, and boost duration $T_{\mathrm{r}\mathrm{e}\mathrm{s}}$ (orange); pathogen escape mutant frequency $x\left(t\right)$ (blue) using a detection threshold $x\left(t\right)>0.05$ to initiate rescue boost (dashed line). (I) Pathogen mean fitness, ${\overline{f}}_p\left(t\right)$, and host payoff, ${\psi }_h\left(t\right)$. (J) Fluxes, ${\mathrm{\Theta }}_p\left(t\right)$ and ${\mathrm{\Theta }}_h\left(t\right)$. (K) Efficiency of maximum-score metastable protocols, ${\eta }_{\mathrm{m}\mathrm{s}}$ (orange), as a function of the pathogen diversity, $\theta$, together with the efficiency of the optimal stationary protocol, $\eta *$ (red dashed). For $\theta <{\theta }_c$, metastable control outperforms stationary control. Parameters: ${ϵ}_0=1$, others as in Fig. 2.