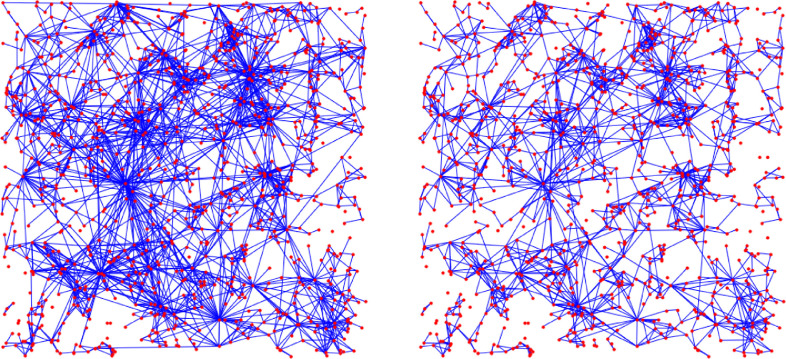
Fig. 9.

Two examples of Geometric Inhomogeneous Random Graphs (GIRGs). The $N=1000$nodes are placed randomly into a square of area N. Each node draws a random fitness from a power law distribution with exponent $\tau =2.95$(left) and $\tau =3.3$(right). We used the same location for nodes and the same underlying uniform variables to simulate fitnesses in both cases: for a uniform variable $U_v\in [0,1],$we set the fitness of node $v$to $W_v^{\left(2.95\right)}:=U_v^{-1/1.95}$on the left, while $W_v^{\left(3.3\right)}:=U_v^{-1/2.3}$on the right. Each pair of nodes with positions x₁, x₂ and weights $w_1,w_2,$respectively, is connected with probability $p^{\left(\tau \right)}=0.5(1\wedge 0.2(w_1^{\left(\tau \right)}{w}_2^{\left(\tau \right)}|x_1-x_2|{}^{-d}\left){}^{\alpha }\right),$where $\alpha =2.5$. Connections are again generated in a coupled way, using the same set of uniform variables for the two pictures, thresholded at p^(2.95)and p^(3.3), respectively.