Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls

Petter Jakobsen; Enrique Garcia-Ceja; Michael Riegler; Lena Antonsen Stabell; Tine Nordgreen; Jim Torresen; Ole Bernt Fasmer; Ketil Joachim Oedegaard

doi:10.1371/journal.pone.0231995

. 2020 Aug 24;15(8):e0231995. doi: 10.1371/journal.pone.0231995

Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls

Petter Jakobsen ^1,^2,^*, Enrique Garcia-Ceja ³, Michael Riegler ^4,⁵, Lena Antonsen Stabell ^1,², Tine Nordgreen ^6,⁷, Jim Torresen ⁵, Ole Bernt Fasmer ^1,², Ketil Joachim Oedegaard ^1,²

Editor: Kyoung-Sae Na⁸

PMCID: PMC7446864 PMID: 32833958

Abstract

Current practice of assessing mood episodes in affective disorders largely depends on subjective observations combined with semi-structured clinical rating scales. Motor activity is an objective observation of the inner physiological state expressed in behavior patterns. Alterations of motor activity are essential features of bipolar and unipolar depression. The aim was to investigate if objective measures of motor activity can aid existing diagnostic practice, by applying machine-learning techniques to analyze activity patterns in depressed patients and healthy controls. Random Forrest, Deep Neural Network and Convolutional Neural Network algorithms were used to analyze 14 days of actigraph recorded motor activity from 23 depressed patients and 32 healthy controls. Statistical features analyzed in the dataset were mean activity, standard deviation of mean activity and proportion of zero activity. Various techniques to handle data imbalance were applied, and to ensure generalizability and avoid overfitting a Leave-One-User-Out validation strategy was utilized. All outcomes reports as measures of accuracy for binary tests. A Deep Neural Network combined with SMOTE class balancing technique performed a cut above the rest with a true positive rate of 0.82 (sensitivity) and a true negative rate of 0.84 (specificity). Accuracy was 0.84 and the Matthews Correlation Coefficient 0.65. Misclassifications appear related to data overlapping among the classes, so an appropriate future approach will be to compare mood states intra-individualistically. In summary, machine-learning techniques present promising abilities in discriminating between depressed patients and healthy controls in motor activity time series.

Introduction

The current practice of assessing mood episodes in affective disorders are subjective observations combined with semi-structured clinical rating scales. Objective methods for assessing affective symptoms are desired [1]. Motor activity is an objective observation of the inner physiological state expressed in behavior patterns, and alterations in activation are essential symptoms of bipolar and unipolar depression [2, 3]. The depressive state is typically associated with reduced daytime motor-activity, increased variability in activity levels and less complexity in activity patterns compared to healthy controls [2]. However, in some bipolar and unipolar depressed patients contradictory motor activity patterns have been observed, characterized by increased mean activity levels, reduced variability and an augmented complexity in activity patterns more similar to that observed in manic patients [4]. Such depressions are commonly associated with irritability, restlessness, and aroused inner tension, in contrast to the general loss of initiative and interest characterizing psychomotor retarded depressions [5].

It has been suggested by Sabelli et al. [6] that mood disorders are diseases of energy fluctuations, and a thermodynamic model of bipolar disorder has been proposed. Simplified the model represents two energies emanating out of a mutual zero point of down-regulated motor retarded depression. The first euphoric energy represents arousal of manic symptoms like inflated self-esteem and increased goal-directed actions. The second agitated energy is associated with aroused inner tension, anxiety and restlessness. The euthymic condition oscillates within a healthy range on both energies. There is evidential support for the thermodynamic hypothesis as amplified levels of euphoric and agitated energy seems present within the manic state [7], and agitated energy seems present in approximately one out of five depressions, regardless of polarity [8].

Motor activity is indisputably an articulation of repeated daily social rhythms in interaction with cyclical biological rhythms, driven by the 24-hour circadian clock interlocked with numerous ultradian rhythmic cycles of 2 to 6 hours [9]. Out of sync biological rhythmic patterns are suggested as essential symptoms of mood episodes [10]. Time series of recurring biological rhythms and day-to-day life patterns are to be considered as complex dynamical systems [11]. Complex dynamical systems rarely categorizes by simple linear models. Therefore, mathematical tools obtained from the field of non-linear complex and chaotic systems have been the traditional method for analyzing and evaluating motor activity recordings [12–14]. Machine learning (ML) techniques have displayed promising results in analyzing data of complex dynamical systems [15, 16], and MLs ability to reveal non-obvious patterns has fairly accurately classified mood state in long-term heart rate variability analysis of bipolar patients [17]. Nonlinear heart rate variability analyses have similarly identified altered cardiovascular autonomic functions in manic patients [18]. Accelerometer recordings are considerably more noisy than heart rate data [19]. Still, motor activity time series hold prodigious potential for various ML approaches. Techniques like Random Forest [20] and neural networks [21, 22] have revealed promising abilities to handle time series of activation data.

A neural network might be understood as a mathematical model, where millions of parameters automatically fine-tunes to optimize the models’ performance [23, 24]. Consequently, insight into the lines of argument is difficult. However, there are methods that allow the interpretation of neural network internals to some extent [25]. Within medical science, there is skepticism of such a black-box method generating calculations without an explanation [26]. However, outcomes from analyses of essential variables of high quality ought to be considered trustworthy, at least when measures to counteract overfitting have been applied [27]. The ensemble learning method of the Random Forest algorithm is robust against overfitting, and the approach might be understood as a woodland of decision trees, where multiple trees look at stochastic parts of the data [28]. Decision trees' decisions are transparent, and lines of argument interpretable [29].

The aim was to investigate if objective biological measures can aid existing diagnostic practice, by applying machine-learning techniques to analyze motor activity patterns from depressed patients and healthy controls.

Materials and methods

Sample characteristics

This is a reanalysis of motor activity recordings originating from an observational cohort study presented in previous papers [12, 13, 30]. The study group consisted of 23 bipolar and unipolar outpatients and inpatients at Haukeland University Hospital, Bergen, Norway. All fulfilled the criteria for a major depression, according to a semi-structured interview based on DSM-IV criteria for mood disorders [31]. The severity of the depressive symptoms was evaluated on the Montgomery and Aasberg Depression Rating Scale (MADRS) at the beginning and conclusion of the motor-activity recordings [32]. 15 of the patients were on antidepressants, some co-medicated with either mood stabilizers or antipsychotics, the rest did not use any psychiatric medications. Further description of the study group is presented in previous papers.

The control group consisted of 32 heathy individuals, all without a history of either psychotic or affective disorders. The majority were shift working hospital staffs. Both datasets are available for other researchers [33]. The Norwegian Regional Medical Research Ethics Committee West approved the study protocol, a written informed consent was obtained from all participants involved in the study, no compensations for participating in the study were given, and all processes were in accordance with the Helsinki Declaration of 1975.

Recording of motor activity

Motor activity was recorded with a wrist-worn actigraph entailing a piezoelectric accelerometer programmed to record the integration of intensity, amount and duration of movement in all directions. The sampling frequency was 32 Hz and movements over 0.05 g recorded. The output was gravitational acceleration units per minute [30]. The Actigraph device was worn continuously throughout the complete recording period.

Machine learning

The basic framework of our ML approach has earlier been presented in a technological conference paper [34], but the method presented here represents a substantial extension of the previous work. Given that the main objective was to classify a user as depressed or not depressed, we proposed the following approach to accomplish this: Each user collected data for d_i consecutive days where d_i represents the number of days collected by participant i. Then, statistical features capturing overall activity levels and variations from each day were extracted [35], resulting in d_i feature vectors per participant, and then normalized per participant to values between zero and one. That is, the normalization parameters (max and min values) were learned from the training set users. The features were extracted in the statistical software R version 3.6.0.

To avoid overfitting, we adopted a Leave-One-User-Out validation strategy, i.e., for each user i, use all the data from all other users not equal to i to train the classifier and test them using the data from user i. In order to obtain the final classification for a particular user, depressed or not depressed, a vector of predictions p is first obtained from the trained classifier. Each entry of p corresponds to the prediction of a particular day. The final label was obtained by majority voting, i.e., output the most frequent prediction from p [27].

Our dataset was imbalanced with 291 depressed and 402 not depressed states, yet it is regarded as a realistic representation of real-world clinical data [36]. As ML algorithms generally have a tendency to favor the most represented class, we tested two different class balancing oversampling techniques for augmenting the minority class [37]. Firstly, we used random oversampling, which duplicates data points selected at random. Secondly, we used SMOTE [38], which creates new synthetic samples that are generated at random from similar neighboring points. Furthermore, we tested three different machine learning classifiers, Random Forest [39], unweighted and weighted Deep Neural Network (DNN) and a weighted Convolutional Neural Network (CNN) [40]. The weighted DNN and CNN use class weights at training time to weight the loss function. The weight for the depressed class was set as wdepressed = α/β where α is the number of instances that belong to the majority class (not depressed) and β are (or maybe denotes) the number of points that belong to the minority class (depressed). The weight for the not depressed class was set as wnondepressed = α/α = 1. This weighting informs the algorithm to pay more attention to the underrepresented class. The weighting parameters were learned from the training set. For the weighted approaches, neither random oversampling nor SMOTE were utilized as this will be double compensating for the class imbalance in the training set.

Random forest is an ensemble method that uses multiple learning models to gain better predictive results. It consists of several decision trees. Each decision tree considers a subset of features to solve the problem at hand. Each subset has only access to a subset of the training data points, consequently leading to a more robust overall performance by increasing the diversity in the forests. The subsets are chosen randomly, and the final prediction is an average from all sub decision trees within the forest [39]. The code was implemented in the statistical software R with the use of the randomForest library [28].

The DNN architecture consisted of two fully connected hidden layers with 128 and 8 units respectively with a rectified linear unit (ReLU) as activation function. After each layer, we applied dropout (p = 0.5) and the last layer has 2 units with a softmax activation function. The CNN architecture entailed two convolutional layers where max pooling and dropout (p = 0.25) were used. Then, two more convolutional layers also applying max pooling and dropout (p = 0.25) followed. Lastly, the data was flattened, and there was a fully connected layer of 512 units with dropout (p = 0.50). Each convolutional layer had a kernel of size 3 with a stride size of 1. The number of kernels for the first two convolutional layers was 16, and 32 for the last 2 layers. The max pooling size was 2. The activation functions of the convolutional layers and the fully connected layer were ReLUs. Finally, a fully connected layer with 2 units and softmax activation function was used to produce the prediction [40]. For the CNN, instead of extracting features, we represented each day as an image with 24 rows and 60 columns. The rows represent the hour of the day, and the columns represent the minute for each particular hour. Each entry is the activity level registered by the device. Missing values were filled with -1, which accounted for 3.6% of all data points. The motivation of using the CNN approach, was the preservation of more information compared to a feature-based approach. With the CNN and the chosen representation, the granularity is at the minute level and there is no to need do feature extraction. On the other hand, for the non-CNN based methods, the features were computed on a daily basis, which can lead to some information being lost. Both networks trained for 30 epochs with a batch size of 32. The code was written in R (version 3.6.0) using the Keras library with Tensorflow 1.13 as the backend. For baseline classifier, we used a classifier that outputs a random class only based on their prior probabilities regardless of the input data. Note that the baseline predictions were computed separately for each of the machine learning methods. Since the baseline was based on random predictions, results may vary slightly across re-runs.

Statistics

The intention of statistical feature extraction from the raw data file is to distillate the dataset into a few variables adaptable for the machine learning algorithms, ideally capturing the essential content of the original dataset [27]. As no established practice exists, a common way to find out what features to select for a given dataset is empirically evaluating different features [41]. The statistical features extracted for this experiment were mean activity level, the corresponding standard deviation (SD) and the proportion of minutes with an activity level of zero. The estimates were chosen due to previous experiences in analyzing accelerometer data with ML [42]. Mean values were calculated from the pre-normalized features per day for each participant, and significance tested with SPSS version 24. Independent Samples T-Test with Levene's Test of Equality of Variances were applied when comparing two groups. One-way ANOVA when comparing more than two groups, followed by Bonferroni corrections to evaluate pairwise differences between groups. A p-value less than 0.05 was considered statistically significant.

Outcome metrics

Since our ML objective was to classify cases as either depressed mood or controls, the outcome of machine learning algorithms were given in measures of accuracy for binary tests [43]. Sensitivity is the fraction of correctly classified conditions related to all conditions and specificity the fraction of controls correctly classified as controls. Weighted recall is an estimate combining sensitivity and specificity equalized according to sample sizes. The positive (PPV) and negative (NPV) predictive values represent the amount of correct classifications related to the amount of wrong classifications of either conditions (positive) or controls (negative). Weighted precision is an estimate combining the predictive values according to sample sizes. Although the estimate Accuracy is a common indicator when reporting outcomes, it does not consider imbalance in the dataset, and therefore potentially presents misrepresentative outcomes. For evaluating the overall performance of the ML classifiers, we used the Matthews Correlation Coefficient (MCC) that is recommended when datasets are imbalanced [44]. MCC gives a coefficient value between minus one and one, and zero indicates a random estimation.

For the interpretability analysis we used the model-agnostic method Partial Dependence Plots (PDPs) to illustrate separately each of the extracted statistical features’ impact on the Random Forest outcome [45]. To generate the plots, the pdp R library was used [46]. Classes were converted to numeric: depressed = 1 and control = 0, and the partial dependence of a set of features of interest zs was estimated by averaging the predictions for each unique value of zs while keeping the other variables fixed [29].

Results

The condition group analyzed in the first ML runs consisted of 10 females and 13 males, aged 42.8 years (standard derivation (SD) = 11 years), and with average actigraph recordings of 12.7 days (SD = 2.8, range 5–18 days). Mean MADRS score at the start of registrations was 22.7 (SD = 4.8), and at the end 20.0 (SD = 4.7). Fifteen persons were diagnosed with unipolar depression and eight with bipolar disorder. The control group consisted of 20 females and 12 males, average age was 38.2 (SD = 13), and the group wore the actigraph for an average of 12.6 days (SD = 3.3, range 8–20) (Table 1).

Table 1. Characteristics of the depressed patients and healthy controls analyzed in the first machine learning run.

	Depressed patients	Healthy Controls	t-test^*
Label	Condition	Control
Days¹	291	402
N	23	32
Gender (male/female)	13 / 10	12 / 20
Age	42.8 (11.0)	38.2 (13.0)	p = 0.170
Days used Actigraph	12.7 (2.8)	12.6 (2.3)	p = 0.897
Diagnosis (unipolar/bipolar)	15 / 8
MADRS at start	22.7 (4.8)
MADRS at end	20.0 (4.7)
Extracted Statistical Features:
Mean Activity	190.05 (81.44)	286.59 (81.10)	p < 0.001
SD²	300.54 (95.86)	405.10 (99.7)	p < 0.001
Proportion of Zeros³	0.385 (0.154)	0.299 (0.086)	p = 0.010

Open in a new tab

All data are given as mean (standard derivation), if not otherwise specified.

* Independent Samples T-Test with Levene's Test of Equality of Variances, significance level p < 0.05.

¹ Number of 24-h sequences analyzed.

² Standard derivation of mean activity.

³ Ratio of minutes with an activity level of zero.

The best performing ML algorithm in the first run was the weighted CNN approach, correctly classifying 65% of the depressed patients as conditions (sensitivity: 0.65), with a true negative rate of 0.78 (specificity). The overall capabilities of the algorithm to classify both depressions and controls were 0.73 (weighted recall), and overall performance was 0.44 (MCC). Class balancing techniques improved the performance of both of the unweighted ML approaches. Random Forest with SMOTE oversampling technique achieved a sensitivity of 0.61, weighted recall of 0.69 and a MCC of 0.36. In the DNN experiments, random oversampling performed best, with a sensitivity of 0.52, weighted recall of 0.69 and a MCC of 0.35, even though SMOTE achieved a higher sensitivity (0.57). The weighted DNN approach achieved a weighted recall of 0.65 and a MCC of 0.29 (Table 2).

Table 2. Machine learning classification results (1st run) in motor activity time series from depressed patients (n = 23) and healthy controls (n = 32).

Machine Learning Approach	Class Balancing Technique	Classification results by label
		Sensitivity	Specificity	Weighted Recall	PPV	NPV	Weighted Precision	Accuracy	MCC	TP	TN	FP	FN
	Baseline	0.22	0.75	0.53	0.38	0.57	0.49	0.53	−0.4	5	24	8	18
Random Forest	No oversampling	0.44	0.75	0.62	0.56	0.65	0.61	0.62	0.19	10	24	8	13
	Random oversampling	0.52	0.75	0.65	0.60	0.69	0.65	0.65	0.28	12	24	8	11
	SMOTE	0.61	0.75	0.69	0.64	0.73	0.69	0.69	0.36	14	24	8	9
	Baseline	0.22	0.88	0.60	0.56	0.61	0.59	0.60	0.12	5	28	4	18
Deep	No oversampling	0.43	0.84	0.67	0.67	0.68	0.67	0.67	0.31	10	27	5	13
Neural Network	Random oversampling	0.52	0.81	0.69	0.67	0.70	0.69	0.69	0.35	12	26	6	11
	SMOTE	0.57	0.75	0.67	0.62	0.71	0.67	0.67	0.32	13	24	8	10
Weighted Deep	Baseline	0.22	0.88	0.60	0.56	0.61	0.59	0.60	0.12	5	28	4	18
Neural Network	No oversampling	0.61	0.69	0.65	0.58	0.71	0.66	0.65	0.29	14	22	10	9
Weighted Convolutional	Baseline	0.35	0.59	0.49	0.38	0.56	0.48	0.49	−0.06	8	19	13	15
Neural Network	No oversampling	0.65	0.78	0.73	0.68	0.76	0.73	0.73	0.44	15	25	7	8

Open in a new tab

TP: True Positives (condition cases classified correctly as labeled).

FN: False Negatives (condition cases misclassified as control cases).

TN: True Negatives (control cases classified correctly as labeled).

FP: False Positives (controls cases misclassified as condition cases).

Sensitivity: True Positive Rate; TP / (TP + FN). Specificity: True Negative Rate; TN / (TN + FP). Weighted Recall: (Sensitivity x (TP + FN)) + (Specificity x (TN + FP)) / (TP + FN + TN + FP). PPV: Positive Predictive Value; TP / (TP + FP). NPV: Negative Predictive Value: TN / (TN + FN). Weighted Precision: (PPV x (TP + FN)) + (NPV x (TN + FP)) / (TP + FN + TN + FP). Accuracy: (TP + TN) / (TP + TN + FP + FN). MCC: Matthews Correlation Coefficient: ((TP x TN)–(FP x FN)) / sqrt ((TP + FP) x (TP + FN) x (TN + FP) x (TN + FN)).

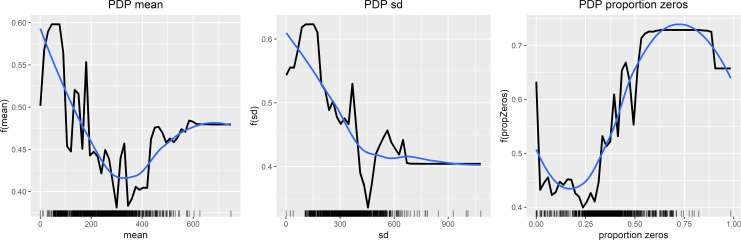
The interpretability analysis of the Random Forest classifier is presented in a partial dependence plot for each analyzed feature (Fig 1). Regarding the mean activity level and standard deviation of mean activity, the overall tendency was decreasing values associated with a condition classification. The trend differs for the proportion of zero activity, where increasing percentage was associated with condition predicted as outcome. Similar overall tendencies were statistical observable between the groups (Table 1), as the depressed patients were significantly lower in mean activity (p < 0.001) and SD of mean activity (p < 0.001), and had elevated ratios of minutes with an activity level of zero (p = 0.010) compared to controls.

As an attempt to capture the quintessence of the misclassified groups, the false cases were commonly identified as misclassifications in the five previous mentioned ML algorithms; weighted CNN, weighted DNN, DNN (SMOTE and random oversampling) and Random Forest (SMOTE). Six conditions were constantly classified falsely (FN) in all five outcomes. There were no significant differences (t-test) when comparing FN and the correctly classified depressions (TP) on MADRS scores. Fewer controls were commonly misclassified (n = 4). For that reason, the false positives group (FP) consisted of all controls misclassified in at least three out of five predicted outcomes (n = 7). When comparing all four outcome groups, FN, FP, TP and true negative controls (TN), we found ANOVA significant group differences for all the analyzed statistical features (p < 0.001) (Table 3). There were no significant group differences (ANOVA) for age composition and the number of days the participants wore the Actigraph.

Table 3. Characteristics of classification results by predicted condition from the 1st machine learning run.

	Predicted groups
	True Positives	False Negatives	True Negatives	False Positives	ANOVA^*
Label	Condition	Condition	Control	Control
N (Days¹)	17 (219)	6 (72)	25 (309)	7 (93)
Mean Activity	159.68 (68.34)^a^/b	276.09 (47.10)^b	313.31 (68.08)^a^/^c	191.16 (42.94)^c	F(3,51) = 21.76, p < 0.001
SD²	263.61 (79.22)^a^/^d	405.18 (50.75)^d	433.63 (91.29)^a^/^e	303.23 (51.92)^e	F(3,51) = 16.93, p < 0.001
Proportion of Zeros³	0.435 (0.106)^f^/^d	0.245 (0.191)^d	0.295 (0.064)^f	0.312 (0.147)	F(3,51) = 7.59, p < 0.001

Open in a new tab

All data are given as mean (standard derivation), if not otherwise specified.

*One-way ANOVA, significance level p < 0.05.

¹ Number of 24-h sequences.

² Standard Derivation of mean activity.

³ Ratio of minutes with an activity level of zero.

Post hoc Bonferroni tests (significance level p < 0.05).

^a p < 0.001—TP compared to TN.

^b p = 0.002—FN compared to TP.

^c p < 0.001—FP compared to TN.

^d p = 0.003—FN compared to TP.

^e p = 0.002—FP compared to TN.

^f p = 0.001—TP compared to TN.

As shown in Table 3 the TP conditions have Bonferroni significantly reduced mean activity compared to both FN conditions (p = 0.002) and TN controls (p < 0.001). The TP conditions had also Bonferroni significant decreased SD compared to FN conditions (p = 0.003) and TN controls (p < 0.001). Furthermore, the portions of minutes with an activity level of zero were significantly higher for TP compared to FN (p = 0.003) and TN (p = 0.001). There were no Bonferroni significant differences between the misclassified depressions (FN) and the two control groups (TN + FP), but the misclassified control group (FP) had significantly reduced mean activity (p < 0.001) and SD (p = 0.002) compared to TN controls.

For the second ML runs, the six patients identified as the FN condition group of the first ML runs were omitted from the analysis. This time the condition group consisted of 7 females and 10 males, with an average age of 45.2 (SD = 10.4) years, and with average actigraph recordings of 12.7 (SD = 3.0, range 5–18) days. Eleven were diagnosed with unipolar depression and six with bipolar disorder (Table 4).

Table 4. Characteristics of depressed patients and healthy controls analyzed in the 2nd machine learning run.

	Depressed patients	Healthy Controls	t-test^*
Label	Condition	Control
Days¹	219	402
N	17	32
Gender (male/female)	10 / 7	12 / 20
Age	45.2 (10.4)	38.2 (13.0)	p = 0.060
Days used Actigraph	12.9 (1.8)	12.6 (2.3)	p = 0.624
Diagnosis (unipolar/bipolar)	11 / 6
MADRS at start	22.0 (5.1)
MADRS at end	19.4 (4.6)
Extracted Statistical Features:
Mean Activity	159.68 (68.34)	486.59 (81.10)	p < 0.001
SD²	263.61 (79.22)	405.10 (99.87)	p < 0.001
Proportion of Zeros³	0.435 (0.106)	0.299 (0.086)	p < 0.001

Open in a new tab

All data are given as mean (standard derivation), if not otherwise specified.

* Independent Samples T-Test with Levene's Test of Equality of Variances, significance level p < 0.05.

¹ Number of 24-h sequences analyzed.

² Standard Derivation of mean activity.

³ Ratio of minutes with an activity level of zero.

DNN with SMOTE oversampling technique performed unmatched with an overall weighted accuracy (MCC) of 0.65, a true positive rate of 0.82 (sensitivity), a true negative rate of 0.84 (specificity) and a weighted recall of 0.84. Random oversampling DNN achieved a sensitivity of 0.82, weighted recall of 0.80 and a MCC of 0.58, and weighted DNN performed with a similar sensitivity, a weighted recall of 0.78 and a MCC of 0.55. Overall, the DNN approaches performed a cut above the rest, as negative predictive values (NPV) around 0.90 indicates a limited number of depressions incorrectly classified as controls. The best performing Random Forest approach (SMOTE) achieved a MCC of 0.53 and a weighted recall of 0.78. Weighted CNN performed with a MCC of 0.46 and weighted recall of 0.76 (Table 5).

Table 5. Machine learning classification results (2nd run) in motor activity time series of motor retarded depressed patients (n = 17) and healthy controls (n = 32).

Machine Learning Approach	Class Balancing Technique	Classification results by label
		Sensitivity	Specificity	Weighted Recall	PPV	NPV	Weighted Precision	Accuracy	MCC	TP	TN	FP	FN
	Baseline	0.18	0.75	0.55	0.27	0.63	0.51	0.55	−0.08	3	24	8	14
Random Forest	No oversampling	0.47	0.84	0.71	0.62	0.75	0.70	0.71	0.34	8	27	5	9
	Random oversampling	0.65	0.81	0.76	0.65	0.81	0.76	0.76	0.46	11	26	6	6
	SMOTE	0.76	0.78	0.78	0.65	0.86	0.79	0.78	0.53	13	25	7	4
	Baseline	0.06	0.91	0.61	0.25	0.64	0.51	0.61	−0.06	1	29	3	16
Deep	No oversampling	0.53	0.91	0.78	0.75	0.78	0.77	0.78	0.48	9	29	3	8
Neural Network	Random oversampling	0.82	0.78	0.80	0.67	0.89	0.81	0.80	0.58	14	25	7	3
	SMOTE	0.82	0.84	0.84	0.74	0.90	0.84	0.84	0.65	14	27	5	3
Weighted Deep	Baseline	0.06	0.88	0.59	0.20	0.64	0.49	0.59	−0.10	1	28	4	16
Neural Network	No oversampling	0.82	0.75	0.78	0.64	0.89	0.80	0.78	0.55	14	24	8	3
Weighted Convolutional	Baseline	0.18	0.78	0.57	0.30	0.64	0.52	0.57	−0.05	3	25	7	14
Neural Network	No oversampling	0.65	0.81	0.76	0.65	0.81	0.76	0.76	0.46	11	26	6	6

Open in a new tab

TP: True Positives (condition cases classified correctly as labeled).

FN: False Negatives (condition cases misclassified as control cases).

TN: True Negatives (control cases classified correctly as labeled).

FP: False Positives (controls cases misclassified as condition cases).

To illustrate the characteristics of the misclassified condition and control groups of the second ML runs, we looked to the misclassifications of the DNN approaches that performed a cut above the rest. Three condition and five control cases were commonly falsely classified. When comparing the four outcome groups (TP, FN, TN and FP) we found statistically significant ANOVA differences (p < 0.001) for all the analyzed statistical features (Table 6). There were no significant differences (t-test) for MADRS scores, mean age and days the Actigraph was worn when comparing the TP and FN conditions groups (t-test). However, there were significant group differences (ANOVA) for age composition when comparing the four outcome groups (F (3, 45) = 3.57, p < 0.021), but no significant differences for number of days the participants wore the Actigraph. The FN group consisted of two males and one female, one diagnosed with bipolar depression and two with unipolar. The FP group included one male and four females.

Table 6. Characteristics of classification results by predicted condition from the second machine learning run.

	Predicted groups
	True Positives	False Negatives	True Negatives	False Positives	ANOVA^*
Label	Condition	Condition	Control	Control
N (Days¹)	14 (176)	3 (43)	27 (335)	5 (67)
Mean Activity	136.78 (50.18)^a^/^b	266.47 (13.71)^b	304.90 (74.05)^a^/^c	187.70 (29.06)^c	F(3,45) = 23.32, p < 0.001
SD²	239.59 (64.38)^a	375.70 (19.56)	424.79 (95.10)^a^/^d	298.77 (41.90)^d	F(3,45) = 16.93, p < 0.001
Proportion of Zeros³	0.454 (0.107)^a	0.347 (0.038)	0.283 (0.084)^a	0.383 (0.026)	F(3,45) = 12.33, p < 0.001

Open in a new tab

All data are given as mean (standard derivation), if not otherwise specified.

* One-way ANOVA, significance level p < 0.05.

¹ Number of 24-h sequences.

² Standard Derivation of mean activity.

³ Ratio of minutes with an activity level of zero.

Post hoc Bonferroni tests (significance level p < 0.05).

^a p < 0.001—TP compared to TN.

^b p = 0.014—FN compared to TP.

^c p < 0.002—FP compared to TN.

^d p = 0.016—FP compared to TN.

As shown in Table 6, the TP conditions presents Bonferroni significantly reduced mean activity compared to FN conditions (p = 0.014) and TN controls (p < 0.001). The FP controls presents significantly reduced mean activity levels compared to TN controls (p < 0.002). The SD of mean activity is significantly reduced for TP conditions compared to TN controls (p < 0.001), and for FP controls compared to TN controls (p = 0.016). For the proportion of minutes with an activity level of zero, TP conditions presents significantly increased portions compared to TN controls (p < 0.001). There were no Bonferroni significant differences between the misclassified depressions (FN) and the two control groups (TN + FP), as well as between the misclassified controls (FP) and the two condition groups (TP + FN).

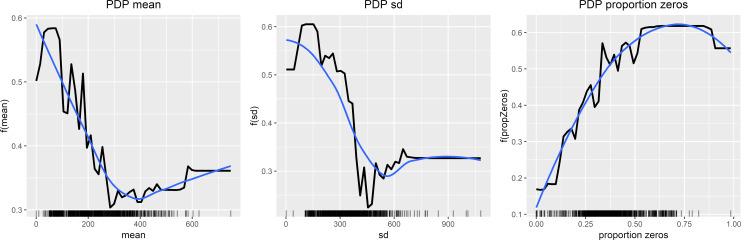
Fig 2 presents the interpretability analysis of the second runs’ Random Forest classifier, illustrating the features’ behavior in the algorithm and their impact on the decisions. The overall tendencies observed in the plots look more defined and stronger than trends in the PDPs of the first ML run. This is as expected, due to the identical data analyzed with a reduced condition group. Similar to the observed significant group differences presented in Table 4, decreasing values of mean activity and standard deviation of mean activity, as well as increasing proportion of zero activity associates with the condition state classification. Furthermore, these trends reflect the significant differences between the four groups presented in Table 6.

Discussion

In our quest to answer the objective of the study, we have tested three different machine learning classifiers analyzing an imbalanced dataset with a larger control group than condition group. ML´s ability to discriminate between depressed patients and healthy controls seems generally promising, as our results are substantially above both random and the baseline predictions. According to our experiment, the Deep Neural Network algorithm seems to be the preeminent ML approach to discriminate between depressed patients and healthy controls in motor activity data. The most optimistic overall result was attained by DNN with the SMOTE oversampling technique, classifying 82% of the depressed patients correctly and 84% of the controls. Random oversampling DNN and weighted DNN also coped with classifying 82% of the depressions correctly, but achieved only to classify respectively 78% and 75% of the controls correctly. However regardless of the outcome, all machine learning approaches utilized in this experiment achieved better results than what was found in a previous study employing a nonlinear discriminant function statistical analysis to differentiate between mood states in 24 hours motor activity recordings of bipolar inpatients [14]. This method managed to classify manic and mixed states rather accurately, but 42% of the depressions misclassified as manic. The misclassification is explained by the fact that depressed patients appear to be a complex and varied group, as some patients presents manic-like motor activity patterns in their depressive state. Therefore, it is more appropriate to compare this study’s results with the results of our experiment's first ML run. In the second ML run, the depressed patients misclassified in the first ML run were omitted from analyzes, as their motor activity patterns looked more analogous to the correctly classified controls, and seem to have contributed only as noisy confusion in the first analysis. Regarding the manic-like patterns, it is previously demonstrated that the motor activity patterns of mania look more similar to those of healthy controls than depressive patients [2].

The rationale behind doing a second ML run omitting the misclassification was not to make the classification problem easier. As the purpose of this study was to investigate if activity measures can aid clinical diagnostics, we needed to recognize the possible presence of agitation in depression due to the significant differences in motor activity patterns. A study by Krane-Gartiser and colleagues [4] investigated group differences between unipolar depressed inpatients with and without motor retardation in 24 hours of motor activity recordings. Depressions without motor retardation were found to have increased mean activity levels; reduced variability compared to the motor retarded patients, as well as augmented complexity in activity patterns. The left out patients of this experiment had significantly increased mean activity compared to the patients involved in the second analysis. The variability measure reported by this previous study is the coefficient of variation (CV) [4], a ratio estimated from SD divided by the mean. Both CV and SD are estimates of variance, expressing the stability of the mean in a time series [47]. Based on the numbers presented in Table 3, the excluded patient group (FN) appears to have reduced CV compared to the others patients (TP). Furthermore, previous studies of the complete current study population have identified increased daytime variability in activity levels for the depressed patients compared to the controls, as well as reduced complexity in daytime activity for the depressed patients [13]. Sample entropy, the nonlinear index of complexity, was not estimated for this experiment. According to experiences within this research group, it is problematic to estimate sample entropy from time series containing longer durations of zero activity, like 24-hour sequences. All series become distinctly ordered, and the ability to differentiate between groups turn out to be significantly reduced. Consequently, sample entropy is applicable only for ultradian periods of more or less continuous activity. Nevertheless, overall it is a reasonable assumption that the left out patients of this experiment are quite similar to the group of unipolar patients without motor retardation reported on by Krane-Gartiser et al.

We have investigated a heterogeneous patient group consisting of unipolar and bipolar depressed inpatients and outpatients. No differences between depressed inpatients and outpatients have previously been identified [48]. According to previous studies, unipolar and bipolar depressions seem to resemble each other in 24-hour motor activity [4, 49]. On the other hand, psychomotor restlessness appears associated with bipolar depression, and the feature seems to differentiate bipolar disorder from unipolar depressions [50]. In our sample, this does not seem to be the case as the ratio of unipolar and bipolar cases equally distributes in both the analyzed and left out patients groups. Also, the proportion of omitted depressions without motor retardation harmonizes with existing evidence as agitated energy seems present in approximately one out of five depressions [8]. Consequently, our promising ML results then only derivate from comparing the activity patterns of motor retarded depressed patients to controls.

Previous studies on accelerometer data and mood disorders have advised against applying ML in smaller samples, mainly due to the risk of overfitting producing untrustworthy results [14]. Overfitting is a phenomenon occurring when an ML algorithm trains itself to perfect predictions on a specific dataset, but then predicts poorly on new data due to systematic bias incorporated in the judgement model. In our experiments, we applied the Leave-One-User-Out validation strategy to minimize the risk of overfitting as recommended. In addition, our findings are in line with existing knowledge. Therefore, our results may be regarded as credible.

The most optimistic individual specificity result accomplished by DNN in the second ML run represents most likely the ML algorithms’ tendency to favor the majority class. So when DNN without oversampling achieved a specificity (true negative rate) of 0.91 by analyzing the unprocessed and imbalanced datasets, the sensitivity was only 0.53. The most optimistic discriminating DNN approaches applied either oversampling techniques or weighting to deal with the imbalance problem. Still, weighted precision outcomes between 0.80 and 0.84 indicates a substantial number of misclassifications, probably related to data overlapping among the falsely classified classes demonstrated in Table 6. Combined, these misclassified subjects establish a gray area of intersecting activation patters, probably partly related to individual differences within the groups, as some people are natural slackers and others are born highly active. Anyhow, little is known about the control group beyond age, gender and the absence of a history of either affective or psychotic disorders. For gender, no differences in activation have previously been identified, but physical properties such as older age and higher body mass index have previously been found to affect mean motor activity [14]. There was no information on body mass index in the dataset, but we did find age differences between the outcome groups in the second ML run. Furthermore, there was no information on external influences like seasonal time of year when the data were collected, but this has previously been considered not relevant for the evaluation of motor activity recordings [48]. On the other hand, at higher latitudes with significant seasonal change in solar insolation, hours of daylight and social rhythms, one should expect a seasonal expression in motor activity [51]. The current dataset was collected at latitude 60.4 N, a position associated with substantial seasonal change in natural light and length of day. Various psychiatric and somatic drugs may also influence motor activity patterns [14], but besides lack of medical data on the controls, the sample size is too small for such sub analyzes. Finally, being in employment could be a possible confounder of why depressed patients present lower overall activity levels than the control group.

Beside the small sample size, the main limitation of the study was the comparison between depressed patients and healthy controls. Firstly, this may have introduced errors and noise into results as individualistic divergent activity levels might have affected group differences. Secondly, although intra-individualistic comparisons suggests that the bipolar manic state is associated with increased mean activity levels, no compelling evidence has been found when comparing manic patients to healthy controls [2]. Thirdly, euthymic individuals with bipolar disorders have been found to have generally reduced mean motor activity, prolonged sleep and reduced sleep quality compared to healthy controls [52]. Therefore, a more appropriate approach would have been to compare a group of depressed patients to themselves in the euthymic state, as to identify actual alterations in motor activity related to changes in mood state [53]. To our knowledge, no such dataset exists. ML analyzes in such an intra-individualistic sample, may provide analyzes beyond the 24-h circadian cycles studied in this experience. For instance, differences between morning and evening, active and non-active periods and sleep patterns, as well as activity differences between weekdays and weekends, could be more feasible in intra-individualistic samples. In the present work, we have analyzed a possible set of statistical features extracted from activity time series, and displayed how accurate machine learning models can be trained with those. As a future direction, the utilized public dataset provides the possibility to explore the use of additional statistical features.

In conclusion, this study has illustrated the promising abilities of various machine learning algorithms to discriminate between depressed patients and healthy controls in motor activity time series. Furthermore, that the machine learning´s ways of finding hidden patterns in the data correlates with existing knowledge from previous studies employing linear and nonlinear statistical methods in motor activity. In our experiment, Deep Neural Network performed unsurpassed in discriminating between conditions and controls. Nonetheless, considering that the analyzed sample was both small and heterogeneous, we should be careful when concluding on which algorithm was the most accurate. Finally, we have enlightened the heterogeneity within depressed patients, as it is recognizable in motor activity measurements.

Acknowledgments

This publication is part of the INTROducing Mental health through Adaptive Technology (INTROMAT) project.

Data Availability

The data can be accessed via: http://datasets.simula.no/depresjon/ Or directly downloaded from: https://doi.org/10.5281/zenodo.1219550.

Funding Statement

The Norwegian Research Council (agreement 259293) funded this project. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. SINTEF Digital provided support in the form of salaries for author [EG-C], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. Part of the authors [EG-C] work was done when he was former employed at the University of Oslo; all work done after he joined SINTEF Digital has been done on the authors’ free time. SINTEF Digital is not paying for this study. The specific roles of the authors are articulated in the ‘author contributions’ section.

References

1.Bauer M, Andreassen OA, Geddes JR, Kessing LV, Lewitzka U, Schulze TG, et al. Areas of uncertainties and unmet needs in bipolar disorders: clinical and research perspectives. The Lancet Psychiatry 2018;5:930–39. 10.1016/S2215-0366(18)30253-0 [DOI] [PubMed] [Google Scholar]
2.Scott J, Murray G, Henry C, Morken G, Scott E, Angst J, et al. Activation in bipolar disorders: A systematic review. JAMA Psychiatry. 2017;74(2):189–96. 10.1001/jamapsychiatry.2016.3459 [DOI] [PubMed] [Google Scholar]
3.Burton C, McKinstry B, Szentagotai Tătar A, Serrano-Blanco A, Pagliari C, Wolters M. Activity monitoring in patients with depression: A systematic review. Journal of Affective Disorders. 2013;145(1):21–8. 10.1016/j.jad.2012.07.001 [DOI] [PubMed] [Google Scholar]
4.Krane-Gartiser K, Henriksen T, Vaaler AE, Fasmer OB, Morken G. Actigraphically assessed activity in unipolar depression: a comparison of inpatients with and without motor retardation. Journal of clinical psychiatry. 2015;76(9):1181–7. 10.4088/JCP.14m09106 [DOI] [PubMed] [Google Scholar]
5.Faedda GL, Marangoni C, Reginaldi D. Depressive mixed states: A reappraisal of Koukopoulos׳criteria. Journal of Affective Disorders. 2015;176:18–23. 10.1016/j.jad.2015.01.053 [DOI] [PubMed] [Google Scholar]
6.Sabelli HC, Carlson-Sabelli L, Javaid JI. The thermodynamics of bipolarity: A bifurcation model of bipolar illness and bipolar character and its psychotherapeutic applications. Psychiatry. 1990;53(4):346–68. 10.1080/00332747.1990.11024519 [DOI] [PubMed] [Google Scholar]
7.Dilsaver SC, Chen YR, Shoaib AM, Swann AC. Phenomenology of mania: evidence for distinct depressed, dysphoric, and euphoric presentations. American Journal of Psychiatry. 1999;156(3):426–30. 10.1176/ajp.156.3.426 [DOI] [PubMed] [Google Scholar]
8.Tondo L, Vázquez GH, Pinna M, Vaccotto PA, Baldessarini RJ. Characteristics of depressive and bipolar disorder patients with mixed features. Acta Psychiat Scand. 2018;138(3):243–52. 10.1111/acps.12911 [DOI] [PubMed] [Google Scholar]
9.Bourguignon C, Storch K-F. Control of Rest:Activity by a Dopaminergic Ultradian Oscillator and the Circadian Clock. Front. Neurol. 2017;8(614). [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Alloy LB, Ng TH, Titone MK, Boland EM. Circadian Rhythm Dysregulation in Bipolar Spectrum Disorders. Current Psychiatry Reports. 2017;19(4):21 10.1007/s11920-017-0772-z [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Glass L, Kaplan D. Time series analysis of complex dynamics in physiology and medicine. Medical progress through technology. 1993;19:115–. [PubMed] [Google Scholar]
12.Fasmer EE, Fasmer OB, Berle JØ, Oedegaard KJ, Hauge ER. Graph theory applied to the analysis of motor activity in patients with schizophrenia and depression. PloS one. 2018;13(4):e0194791 10.1371/journal.pone.0194791 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Hauge ER, Berle JØ, Oedegaard KJ, Holsten F, Fasmer OB. Nonlinear analysis of motor activity shows differences between schizophrenia and depression: a study using Fourier analysis and sample entropy. PloS one. 2011;6(1):e16291 10.1371/journal.pone.0016291 [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Scott J, Vaaler AE, Fasmer OB, Morken G, Krane-Gartiser K. A pilot study to determine whether combinations of objectively measured activity parameters can be used to differentiate between mixed states, mania, and bipolar depression. International Journal of Bipolar Disorders. 2017;5(1):5 10.1186/s40345-017-0076-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Pathak J, Wikner A, Fussell R, Chandra S, Hunt BR, Girvan M, et al. Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2018;28(4):041101. [DOI] [PubMed] [Google Scholar]
16.Wan ZY, Vlachas P, Koumoutsakos P, Sapsis T. Data-assisted reduced-order modeling of extreme events in complex dynamical systems. PloS one. 2018;13(5):e0197704 10.1371/journal.pone.0197704 [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Valenza G, Nardelli M, Lanatà A, Gentili C, Bertschy G, Paradiso R, et al. Wearable Monitoring for Mood Recognition in Bipolar Disorder Based on History-Dependent Long-Term Heart Rate Variability Analysis. IEEE Journal of Biomedical and Health Informatics. 2014;18(5):1625–35. 10.1109/JBHI.2013.2290382 [DOI] [PubMed] [Google Scholar]
18.Chang H-A, Chang C-C, Tzeng N-S, Kuo TBJ, Lu R-B, Huang S-Y. Heart rate variability in unmedicated patients with bipolar disorder in the manic phase. Psychiatry and Clinical Neurosciences. 2014;68(9):674–82. 10.1111/pcn.12178 [DOI] [PubMed] [Google Scholar]
19.Fasmer OB, Liao H, Huang Y, Berle JØ, Wu J, Oedegaard KJ, et al. A naturalistic study of the effect of acupuncture on heart-rate variability. Journal of acupuncture and meridian studies. 2012;5(1):15–20. 10.1016/j.jams.2011.11.002 [DOI] [PubMed] [Google Scholar]
20.Kolosnjaji B, Eckert C, editors. Neural network-based user-independent physical activity recognition for mobile devices. International Conference on Intelligent Data Engineering and Automated Learning; 2015: Springer.
21.Inoue M, Inoue S, Nishida T. Deep recurrent neural network for mobile human activity recognition with high throughput. Artificial Life and Robotics. 2018;23(2):173–85. [Google Scholar]
22.Ignatov A. Real-time human activity recognition from accelerometer data using Convolutional Neural Networks. Applied Soft Computing. 2018;62:915–22. [Google Scholar]
23.Greff K, Srivastava RK, Koutník J, Steunebrink BR, Schmidhuber J. LSTM: A search space odyssey. IEEE transactions on neural networks and learning systems. 2017;28(10):2222–32. 10.1109/TNNLS.2016.2582924 [DOI] [PubMed] [Google Scholar]
24.Marblestone AH, Wayne G, Kording KP. Toward an integration of deep learning and neuroscience. Frontiers in Computational Neuroscience. 2016;10:94 10.3389/fncom.2016.00094 [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Ribeiro MT, Singh S, Guestrin C. "Why Should I Trust You?": Explaining the Predictions of Any Classifier. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; San Francisco, California, USA. 2939778: ACM; 2016. p. 1135–44.
26.Bzdok D, Ioannidis JPA. Exploration, Inference, and Prediction in Neuroscience and Biomedicine. Trends in Neurosciences. 2019. [DOI] [PubMed] [Google Scholar]
27.Huys QJM, Maia TV, Frank MJ. Computational psychiatry as a bridge from neuroscience to clinical applications. Nat Neurosci. 2016;19(3):404–13. 10.1038/nn.4238 [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Liaw A, Wiener M. Classification and regression by randomForest. R news. 2002;2(3):18–22. [Google Scholar]
29.Molnar C. Interpretable machine learning: A guide for making black box models explainable. https://christophm.github.io/interpretable-ml-book2018. Available from: https://leanpub.com/interpretable-machine-learning.
30.Berle JO, Hauge ER, Oedegaard KJ, Holsten F, Fasmer OB. Actigraphic registration of motor activity reveals a more structured behavioural pattern in schizophrenia than in major depression. BMC Research Notes. 2010;3:149–. 10.1186/1756-0500-3-149 [DOI] [PMC free article] [PubMed] [Google Scholar]
31.American Psychiatric Association. Diagnostic and statistical manual of mental disorders (4th ed.). Washington DC: American Psychiatric Press; 1994. [Google Scholar]
32.Montgomery S, Asberg A. A new depression scale designed to be sensitive to change. Br J Psychiat. 1979;134. [DOI] [PubMed] [Google Scholar]
33.Garcia-Ceja E, Riegler M, Jakobsen P, Tørresen J, Nordgreen T, Oedegaard KJ, et al., editors. Depresjon: a motor activity database of depression episodes in unipolar and bipolar patients. Proceedings of the 9th ACM Multimedia Systems Conference; 2018. 10.1145/3204949.3208125:ACM [DOI]
34.Garcia-Ceja E, Riegler M, Jakobsen P, Torresen J, Nordgreen T, Oedegaard KJ, et al. , editors. Motor Activity Based Classification of Depression in Unipolar and Bipolar Patients. 2018 IEEE 31st International Symposium on Computer-Based Medical Systems (CBMS); 2018: IEEE. [Google Scholar]
35.Garcia-Ceja E, Osmani V, Mayora O. Automatic Stress Detection in Working Environments From Smartphones’ Accelerometer Data: A First Step. IEEE Journal of Biomedical and Health Informatics. 2016;20(4):1053–60. 10.1109/JBHI.2015.2446195 [DOI] [PubMed] [Google Scholar]
36.Riegler M, Lux M, Griwodz C, Spampinato C, de Lange T, Eskeland SL, et al., editors. Multimedia and medicine: Teammates for better disease detection and survival. Proceedings of the 24th ACM international conference on Multimedia; 2016: ACM.
37.Kotsiantis S, Kanellopoulos D, Pintelas P. Handling imbalanced datasets: A review. GESTS International Transactions on Computer Science and Engineering. 2006;30(1):25–36. [Google Scholar]
38.Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research. 2002;16:321–57. [Google Scholar]
39.Breiman L. Random Forests. Machine Learning. 2001;45(1):5–32. [Google Scholar]
40.LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998;86(11):2278–324. [Google Scholar]
41.Nabih-Ali M, El-Dahshan ELSA, Yahia AS. A review of intelligent systems for heart sound signal analysis. Journal of Medical Engineering & Technology. 2017;41(7):553–63. [DOI] [PubMed] [Google Scholar]
42.Garcia-Ceja E, Brena R, Carrasco-Jimenez J, Garrido L. Long-term activity recognition from wristwatch accelerometer data. Sensors 2014;14(12):22500–24. 10.3390/s141222500 [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Pepe MS. The statistical evaluation of medical tests for classification and prediction. Oxford: Medicine; 2003. [Google Scholar]
44.Boughorbel S, Jarray F, El-Anbari M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PloS one. 2017;12(6):e0177678 10.1371/journal.pone.0177678 [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Friedman JH. Greedy function approximation: a gradient boosting machine. Annals of statistics. 2001:1189–232. [Google Scholar]
46.Greenwell BM. pdp: an R Package for constructing partial dependence plots. The R Journal. 2017;9(1):421–36. [Google Scholar]
47.Fleiss JL, Bigger JT Jr, Rolnitzky LM. The correlation between heart period variability and mean period length. Statistics in Medicine. 1992;11(1):125–9. 10.1002/sim.4780110111 [DOI] [PubMed] [Google Scholar]
48.Krane-Gartiser K, Henriksen TEG, Morken G, Vaaler A, Fasmer OB. Actigraphic assessment of motor activity in acutely admitted inpatients with bipolar disorder. PloS one. 2014;9(2):e89574 10.1371/journal.pone.0089574 [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Krane-Gartiser K, Vaaler AE, Fasmer OB, Sørensen K, Morken G, Scott J. Variability of activity patterns across mood disorders and time of day. BMC psychiatry. 2017;17(1):404–. 10.1186/s12888-017-1574-x [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Oedegaard KJ, Neckelmann D, Fasmer OB. Type A behaviour differentiates bipolar II from unipolar depressed patients. Journal of Affective Disorders. 2006;90(1):7–13. 10.1016/j.jad.2005.10.005 [DOI] [PubMed] [Google Scholar]
51.Pirkola S, Eriksen HA, Partonen T, Kieseppä T, Veijola J, Jääskeläinen E, et al. Seasonal variation in affective and other clinical symptoms among high-risk families for bipolar disorders in an Arctic population. International journal of circumpolar health. 2015;74(1):29671. [DOI] [PMC free article] [PubMed] [Google Scholar]
52.De Crescenzo F, Economou A, Sharpley AL, Gormez A, Quested DJ. Actigraphic features of bipolar disorder: A systematic review and meta-analysis. Sleep Med Rev. 2017;33:58–69. 10.1016/j.smrv.2016.05.003 [DOI] [PubMed] [Google Scholar]
53.Krane-Gartiser K, Asheim A, Fasmer OB, Morken G, Vaaler AE, Scott J. Actigraphy as an objective intra-individual marker of activity patterns in acute-phase bipolar disorder: a case series. International journal of bipolar disorders. 2018;6(1):8–. 10.1186/s40345-017-0115-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0231995.r001

Decision Letter 0

Kyoung-Sae Na

15 May 2020

PONE-D-20-09443

Applying machine learning in motor activity time series of depressed bipolar and unipolar patients.

PLOS ONE

Dear Mr Jakobsen,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

As you see the reviewers' comments, please particularly pay attention to the 'Materials and Methods' and 'Results' section.

We would appreciate receiving your revised manuscript by Jun 29 2020 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

We look forward to receiving your revised manuscript.

Kind regards,

Kyoung-Sae Na, M.D.

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Thank you for stating the following in the Competing Interests section:

'The authors have declared that no competing interests exist.'

We note that one or more of the authors are employed by a commercial company: SINTEF Digital.

Please provide an amended Funding Statement declaring this commercial affiliation, as well as a statement regarding the Role of Funders in your study. If the funding organization did not play a role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript and only provided financial support in the form of authors' salaries and/or research materials, please review your statements relating to the author contributions, and ensure you have specifically and accurately indicated the role(s) that these authors had in your study. You can update author roles in the Author Contributions section of the online submission form.

Please also include the following statement within your amended Funding Statement.

“The funder provided support in the form of salaries for authors [insert relevant initials], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.”

If your commercial affiliation did play a role in your study, please state and explain this role within your updated Funding Statement.

2. Please also provide an updated Competing Interests Statement declaring this commercial affiliation along with any other relevant declarations relating to employment, consultancy, patents, products in development, or marketed products, etc.

Within your Competing Interests Statement, please confirm that this commercial affiliation does not alter your adherence to all PLOS ONE policies on sharing data and materials by including the following statement: "This does not alter our adherence to PLOS ONE policies on sharing data and materials.” (as detailed online in our guide for authors http://journals.plos.org/plosone/s/competing-interests) . If this adherence statement is not accurate and there are restrictions on sharing of data and/or materials, please state these. Please note that we cannot proceed with consideration of your article until this information has been declared.

Please include both an updated Funding Statement and Competing Interests Statement in your cover letter. We will change the online submission form on your behalf.

Please know it is PLOS ONE policy for corresponding authors to declare, on behalf of all authors, all potential competing interests for the purposes of transparency. PLOS defines a competing interest as anything that interferes with, or could reasonably be perceived as interfering with, the full and objective presentation, peer review, editorial decision-making, or publication of research or non-research articles submitted to one of the journals. Competing interests can be financial or non-financial, professional, or personal. Competing interests can arise in relationship to an organization or another person. Please follow this link to our website for more details on competing interests: http://journals.plos.org/plosone/s/competing-interests

Additional Editor Comments (if provided):

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: No

Reviewer #2: Yes

Reviewer #3: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: The authors present the results of a classification analysis using machine learning methods to discriminate between patients with depression and healthy controls based on objective motor activity data collected with actigraph. The results show that objective activity data can be used to discriminate between patients and healthy controls with high accuracy. Using objective sensor data to diagnose and/or monitor symptoms in mental illness is both important and interesting. Several issues require consideration and should be addressed.

MAJOR ISSUES

1. In the machine learning section on line 133 the authors state that the feature vectors were normalised. It is not clear if the features were normalised per participant or across all participants. In cross-validation, the held out data should not be considered when normalising the training data to avoid learning any information from the held out data.

2. In the machine learning section on line 150-153 the authors state how the class weights are computed. However, it is not clear if the class weights are computed on the training set or across the entire dataset. In cross-validation the weights should be computed on the training set only to avoid learning from the held out data.

3. The results section on line 241-242 states “Weighted DNN performed best without class balancing techniques (no oversampling) […]” Using oversampling and class weighting at the same time will double compensate for the class imbalance in the training set and result in a biased classifier.

4. Tables 2 and 5 are not fully visible in the manuscript.

5. Figures 1 and 2 are too blurred to see axis labels and units.

6. The motivation for presenting a second run of the classification analysis without the false negatives identified in the first run is not clear. Is it not just making the classification problem easier by removing some of the “difficult” cases? The difference in mean activity between TP and FP is already demonstrated after the first run.

7. On line 466-468 the authors state that a weighted and random oversampling DNN achieves higher sensitivity and lower specificity. As stated in a previous comment, if the positive class is both weighted higher and oversampled the model is double compensating for the minority class.

8. In table 2 and 5, it is not clear why the baseline results are reported multiple times and why the results of the baselines are different every time.

MINOR ISSUES

9. In the introduction on line 94 the authors state that insight into neural networks is virtually impossible. While it may not be straight forward, there is a large research effort to improve interpretability of neural networks.

10. In the introduction on line 98-99 the authors state that “the random forest classifier is more flexible and less data-sensitive than neural networks.” It is not clear what is meant by “more flexible”. A neural networks with a non-linear activation function and a large hidden layer is a universal function approximator and thus a very flexible model.

11. In the introduction on line 101 the authors state that the random forest algorithm “has been found to predict with approximate similar quality to neural networks.” I think this is highly domain specific. While random forest is a powerful algorithm for many purposes neural networks have been proved to be superior to mostly any other method in areas such as computer vision and speech recognition.

12. It is stated on line 141 that there are 291 depressed and 402 not depressed states, but on line 150-153 ‘depressed’ is said to be majority class and ‘not depressed’ the minority class, which is contradicting.

13. Line 174-177 describes how the features are represented as an image for the CNN. It is not clear how the authors chose this feature representation or why it is appropriate for the classification task.

14. The authors already mentions limitations of comparing the patient and healthy control group. Employment status could be another significant reason why patients with depression present with lower overall activity.

Reviewer #2: This manuscript describes reanalysis of existing data applying machine-learning techniques with various data balance technique for activity patterns in depressed patients and healthy controls, and present promising abilities in discriminating between depressed patients and healthy controls in motor activity time series.

1. In the Part of Material and Methods, the detailed information of record for the motor activity might be necessary in order to achirve the integrity of the manuscript, e.g., how many time points were there in one day? How many days were recorded for each subject? Did the subjects wear the equipment all day long even during night?

2. The description of the ML process is very clear, but I am not sure if the algorithm performance is affected by depressive episode or not.

3. For the CNN, each day was represented as an image with 24 rows and 60 columns. The rows represent the hour of the day, and the columns represent the minute for each particular hour. I have two considerations:

1) I am not sure whether such new arrangement of data bring unnecessary artifact, because the data point at each minute for each hour should not have dependent relationships with a high probability. How do you explain this new data represents?

2) Missing values were filled with -1. I am interested in what distribution of these missing values for all participants? What influence may bring to the CNN?

4. From ML classification results tables, the weighted Models did not show any benefits, while, moreover, the most optimistic overall result were attained by unweighted DNN with the random oversampling technique. So, I wonder how you consider to weight for two conditions as you emphasized in particular: ‘This weighting informs the algorithm to pay more attention to the underrepresented class.’ ?

5. There must be a significant gender difference between the two groups, this might also make some data imbalance as well as recording days, how do you manage it?

6. Last, the manuscript gave one of the conclusions that Deep Neural Network performed preeminent in discriminating between conditions and controls. I suggest that we should be more careful and conservative since the sample is small and patient groups are composed by both bipolar and unipolar.

Reviewer #3: First, I reveal that I did not fully understand all the methods I applied in this study. Therefore, please read this in consideration of this.

Using this activity data through actigraphy, authors studied how to predict the depressive mood state by using various machine learning analysis methods for depression and normal control's activity. Strictly speaking, this study explores which machine learning analysis method has the best performance.

I would like to think high on how this paper tried to overcome overfitting and sample imbalance by applying various analysis techniques precisely. However, while this may simply be meaningful in terms of technical methodology, it remains fundamentally questionable as to the value of this study's hypothesis, the nature of the sample, and how valuable the research was in drawing conclusions.

It may be a good idea to use the activity level to predict the mood state of a patient with a mood disorder, but it is a very poor study in that various variables were not considered. In particular, machine learning by using the most basic values such as the mean of the activity and standard deviation causes too much to be missed. Eventually, this approach will not predict "mood depressed state", but rather predict "activity depressed state" that is supposed to be due to depression. Authors must seriously consider how to interpret and overcome this.

#1. The title appears as if the subject of this study was to differentiate motor activity in patients with bipolar and unipolar depression. It would be better to revise the subject more clearly to reveal the subject of the article.

#2. You need to use universal word in English for Keywords. It would be good to change the word into "actigraphy"

#3. Introduction Line 78~80

I agree that the time series should reflect biological rhythms and changes in daily life patterns. I think this doesn't just mean that it doesn't follow a simple linear model. It may be key to access the given activity data to fit the characteristics of the time series. What strategies did you use in this study to reflect the characteristics of your data, such as biological rhythms?

#4. Materials and methods Line 113~

The description of the sample is insufficient. Was the drug being administered at the time of the study, how long the morbidity of mood disorder was, whether receiving other nonpharmacologic treatments (eg IPSRT) that could affect the condition, were there no compensations for participating in this study, and was the study a simple observational study? If so, the criteria for inclusion and exclusion of this study should be provided. Basically, if one is depressed, he or she will not be able to comply with the study, but it is impressive that there is no significant difference in wearing days. It is necessary to calculate the wearing rate separately. In other words, it is necessary to define what wear days mean.

#5. It would not be easy to perform validation with such a small number of samples. Validation process seems to require more specific and easy to understand technology and methodology. In particular, in this case, if you repeat the learning and validation several times, the samples will eventually overlap and it may not affect the internal connectivity, which may have an impact on consequences. You need some explanation to overcome this.

#6. Please revise the figures and tables to make them readable. It is difficult to recognize.

#7. In the previous studies, authors mentioned that there was no significant difference between unipolar and bipolar depression, but I still have questions about it. Of course, since unipolar depression can be diagnosed as bipolar disorder in the future, it is not easy to make a judgment based on the current diagnosis. However, it is prudent to gather and analyze heterogeneous groups into one group. Analyzing depend on the level of activity, sampling may have its own bias. It is suggested to analyze by dividing unipolar and bipolar. And, if there is data on the normal (euthymic) mood of patients with mood disorders, not normal control people, it is necessary to compare and analyze it. It is also important to distinguish the depressed state of mood disorder from normal people, but it is more important to distinguish the euthymic and depressed mood states of mood disorders.

#8. Statistics Line 188~

How did you deal with the section that could be thought of as sleep? Did you ever think about an activity level of zero throughout the day regardless of sleep or not?

#9. Outcome Metrics 197~

You mean a depressed condition? It would be better to describe it a little more clearly. Calling a condition group is easily confusing. It is recommended to describe it a depressed mood.

#10. Table 1

Even in a healthy control group, it is basically necessary to present and compare the same psychometric values. In this study, MADRS was presented, but the results of this study do not know the mood state of the normal control group.

#11. When data related to sleep are analyzed together, some limitations of activity data can be improved. Consideration should be given to analyzing and presenting sleep data.

#12. I recommend that you try to train activity data by making it more diverse secondary variables. The strength of this data is that it is a time series. In the introduction, the characteristics of time series data and the necessity of proper analysis were explained, but in the present, only a several MLs were applied. Whether it is an analysis according to the circadian rhythm, the difference between weekdays and weekends, the difference between morning and afternoon, the difference between the most active and non-active periods, the irregularity of activities, etc. I think it is necessary. The author should considers the characteristics of the time series as much as possible, and analyzes according to the circadian rhythm, the difference between weekdays and weekends, the difference between the morning and the afternoon, the difference between the most active and non-active periods, irregularities in activities, etc. You need to do a sophisticated analysis with the possibility of creation.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files to be viewed.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2020 Aug 24;15(8):e0231995. doi: 10.1371/journal.pone.0231995.r002

Author response to Decision Letter 0

27 Jun 2020

We thank the editor and reviewers for their helpful comments that we think have contributed significantly to improving the paper. Thus, we have provided an amended manuscript with the major revisions that were recommended. Our responses can be found below, directly below the comments that they address.

Academic editor

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming.

A: Thank you for spotting these errors. We have now updated the submitted revised manuscript in accordance with PLOS ONEs requirements. All use of Symbol Font has been removed, and the title, authors and affiliations page is in accordance with the formatting guidelines.

2. We note that one or more of the authors are employed by a commercial company: SINTEF Digital.

1. Please provide an amended Funding Statement declaring this commercial affiliation, as well as a statement regarding the Role of Funders in your study. If the funding organization did not play a role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript and only provided financial support in the form of authors' salaries and/or research materials, please review your statements relating to the author contributions, and ensure you have specifically and accurately indicated the role(s) that these authors had in your study. You can update author roles in the Author Contributions section of the online submission form.

Please also include the following statement within your amended Funding Statement.

If your commercial affiliation did play a role in your study, please state and explain this role within your updated Funding Statement.

A: We are sorry for this misunderstanding, and have as requested updated the Funding Statement to “SINTEF Digital provided support in the form of salaries for author [EG-C], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. Part of the authors [EG-C] work was done when he was former employed at the University of Oslo; all work done after he joined SINTEF Digital has been done on the authors’ free time. SINTEF Digital is not paying for this study. The specific roles of the authors are articulated in the ‘author contributions’ section.” We have also as requested included the updated Funding Statement text in the cover letter.

A: We have as requested updated the Competing Interests Statement. Now it reads:

“I have read the journal’s policy, and one author of this manuscript has the following competing interests: SINTEF Digital provided support in the form of salaries for author [EG-C]. This does not alter our adherence to PLOS ONE policies on sharing data and materials. The other authors have no competing interests.”

Furthermore, we have as requested included the updated Competing Interests Statement in the cover letter.

Reviewer #1:

The authors present the results of a classification analysis using machine learning methods to discriminate between patients with depression and healthy controls based on objective motor activity data collected with actigraph. The results show that objective activity data can be used to discriminate between patients and healthy controls with high accuracy. Using objective sensor data to diagnose and/or monitor symptoms in mental illness is both important and interesting. Several issues require consideration and should be addressed.

MAJOR ISSUES

A: Thank you for the opportunity to clarify this, for indeed, the normalization was made across users. As suggested by the reviewer, now the normalization was done per participant to avoid learning from the test set, the experiments were rerun, and the results updated accordingly. Overall, the performance decreased a bit for all tested methods; however, the findings remain significant. We have included an improved description of how normalization was done in the machine learning section on line 137-139 “… and then normalized per participant to values between zero and one. That is, the normalization parameters (max and min values) were learned from the training set users.”

A: The class weights were learned from the training set. This has been clarified by adding, “The weighting parameters were learned from the training data” on line 161.

A: We agree with the reviewer’s comment. This was over compensating for the minority class. Because of this, now we only include weighting with no oversampling in our experiments that include the weighted DNN and CNN. This has been described in the manuscript (line 161 - 163): “For the weighted approaches, neither random oversampling nor SMOTE were utilized as this will be double compensating for the class imbalance in the training set.”

4. Tables 2 and 5 are not fully visible in the manuscript.

A: All tables should be in line with PLOS ONEs requirements for tables, and according to instructions: “In Word, tables that run off of the manuscript page can be seen using Draft View.”

5. Figures 1 and 2 are too blurred to see axis labels and units.

A: We agree and Figures 1 and 2 are updated.

A: Thank you for the opportunity to clarify this. In the motor activity literature, to classify the mood state of depression in motor activity is considered a complicated task, as these patients appear to be a heterogeneous group, some presenting more manic-like patterns (deviating mean activity and SD). On the other hand, various agitated features seem present in about 20-25 % of all depressions. In our dataset, there was no information about agitation. For that reason, we excluded the commonly misclassified cases and labeled them as «agitated depressions». Mainly because these cases looked more like the healthy controls, e.g. presented manic-like patterns of mean activity and variability (SD). The intention for our approach was simply to enlighten the heterogeneity of activation patterns within depressed patients (as agitated energy was exhaustively presented in the introduction part). Our intention was not to make the classification problem easier by removing “difficult” cases, but we recognize that this concern should be included in our discussion in the manuscript, and have added a sentence about this (line 438 - 441): “The rationale behind doing a second ML run omitting the misclassification was not to make the classification problem easier. As the purpose of this study was to investigate if activity measures can aid clinical diagnostics, we needed to recognize the possible presence of agitation in depression due to the significant differences in motor activity patterns.”

A: We agree. For our re-run experiments with the weighted DNN and CNN, we did not perform oversampling. The statement is therefore deleted.

8. In table 2 and 5, it is not clear why the baseline results are reported multiple times and why the results of the baselines are different every time.

A: This is because the baseline predictions were obtained along with each of the methods. Since the baseline is based on random predictions, it will vary slightly every time it is run. The following text was added to the manuscript on line 193 - 195:

“Note that the baseline predictions were computed separately for each of the machine learning methods. Since the baseline was based on random predictions, results may vary slightly across re-runs.”

MINOR ISSUES

A: We agree that that sentence was not true. We have reformulated it from "Consequently, insight into the lines of argument are virtually impossible" to "Consequently, insight into the lines of argument is difficult. However, there are methods that allow the interpretation of neural network internals to some extent (25)". (Line 94 -95)

A: We agree that that sentence was imprecise. The sentence is now changed to “The ensemble learning method of the Random Forest algorithm is robust against overﬁtting.” The "and less data-sensitive than neural networks." was dropped, as on second thought, we do not think there is evidence to support such a strong assertion.

A: We agree that this statement is problematic, and consequently have deleted it.

A: Thank you for spotting this error. The text has been fixed to “..the number of instances that belong to the majority class (not depressed) and β are (or maybe denotes) the number of points that belong to the minority class (depressed).” (Line 157-159)

A: A motivation of why a CNN approach was also chosen has been included: “The motivation of using the CNN approach, was the preservation of more information compared to a feature-based approach. With the CNN and the chosen representation, the granularity is at the minute level and there is no need to do feature extraction. On the other hand, for the non-CNN based methods, the features were computed on a daily basis, which can lead to some information being lost. ” at line 185 – 189.

A: We agree that employment status could be a significant reason for higher overall activity, and have added the sentence: “Finally, being in employment could be a possible confounder of why depressed patients present lower overall activity levels than the control group” at line 506 – 508. This is related to a newly added sentence describing the healthy controls: “The majority of the group were shift working hospital staffs” at line 119.

Reviewer #2

This manuscript describes reanalysis of existing data applying machine-learning techniques with various data balance technique for activity patterns in depressed patients and healthy controls, and present promising abilities in discriminating between depressed patients and healthy controls in motor activity time series.

A: We agree with the reviewer that this needs clarification and have added the sentence “The Actigraph device was worn continuously throughout the complete recording period.” (Line 128 – 129) in the Recording of motor activity part. We have furthermore improved the reporting on the actigraphy recordings. When reporting average day’s actigraph recordings, we have supplemented the mean and SD estimate with range (min – max). We have also updated the footnotes of tab. 1 and 4 to read, “Number of 24-h sequences analyzed” for the Days variable, as well as reported the Days variable in table 3 and 6.

2. The description of the ML process is very clear, but I am not sure if the algorithm performance is affected by depressive episode or not.

A: This statement is based on evidence supporting that reduced daytime motor-activity and increased variability are associated with depression. Further, that alterations in motor activity might be a more defining symptom than mood for identifying depression in humans with bipolar disorder (Scott J., et al. Activation in bipolar disorders: A systematic review. JAMA Psychiatry. 2017).

A: The motivation of such an arrangement was to preserve all the information as compared to feature-extraction in which a lot of information is lost. With this image representation all the data points per day are preserved and thus, the temporal relations are captured, thus, allowing the CNN to use that information. A motivation of why this representation was used has been included in the text (line 185 – 189): “The motivation of using a CNN is because with this approach, more information is preserved as compared to a feature-based approach. With the CNN and the chosen representation, the granularity is at the minute level and there is no need to do feature extraction. On the other hand, for the non-CNN based methods, the features were computed on a daily basis which can lead to some information being lost”.

2) Missing values were filled with -1. I am interested in what distribution of these missing values for all participants? What influence may bring to the CNN?

A: The percentage of missing values has been added to the manuscript: “Missing values were filled with -1 which accounted for 3.6% of all data points” at line 185. This may have an impact on the model; however, the percentage of missing values is small.

A: Thank you for the opportunity to clarify this. Based on the comments from one of the reviewers (reviewer #1), we rerun the experiments without including oversampling techniques to the weighted models since this would have the effect of double compensating the minority class.

5. There must be a significant gender difference between the two groups, this might also make some data imbalance as well as recording days, how do you manage it?

A: We agree with the reviewer that there must be a significant gender difference between the two groups of patients and controls. However, we have not looked at this topic for two reasons. Firstly, because the sample is too small to do gender sub analyzes. Secondly, because previous studies of motor activity in mood disorders have found no differences in activation between gender. The second reason is stated in the manuscript “For gender, no differences in activation have previously been identified” in line 494 and 495.

A: We agree with this suggestion and have changed the conclusion to; “In our experiment, Deep Neural Network performed unsurpassed in discriminating between conditions and controls. Nonetheless, considering that the analyzed sample was both small and heterogeneous, we should be careful when concluding on which algorithm was the most accurate.” (Line 531- 534)

Reviewer #3

First, I reveal that I did not fully understand all the methods I applied in this study. Therefore, please read this in consideration of this.

A: We agree, and have changed the title of the manuscript correspondingly, “Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls.”

#2. You need to use universal word in English for Keywords. It would be good to change the word into "actigraphy"

A: Good point, this has been changed.

#3. Introduction Line 78~80

A: This is a limitation of our study sample. We have not applied any specific strategy to reflect the characteristics of biological rhythms in our data, beyond analyzing 24-h circadian cycles. In our opinion, to look deeper into the disrupted biological rhythmic patterns associated with depression, we would have needed intra-individual data to do an appropriately comparison of mood state differences. Anyway, we have supplemented the manuscript with the following text (line 519 - 523). “ML analyzes in such an intra-individualistic sample, may provide analyzes beyond the 24-h circadian cycles studied in this experience. For instance differences between morning and evening, active and non-active periods and sleep patterns, as well as activity differences between weekdays and weekends, could be more feasible in intra-individualistic samples”, at the end of the paragraph discussing the need for intra-individualistic data on depression.

#4. Materials and methods Line 113~

A: We agree that the sample might appear somewhat superficially described, but as this is a reanalysis of motor activity recordings originating from a study presented in several previous papers, we have referred to these for detailed description. The original study was an observational cohort study (now mentioned in line 108) of depressed patients in traditional treatment for an ongoing major depression at a Norwegian psychiatric hospital, almost 20 years ago. There was no compensation for participating in the study and no information on duration of mood disorder. We have now inserted a new sentence into the manuscript: “no compensations for participating in the study were given” (line 122).

Since this sample is too small for sub analyzes of drug groups, we did not report on psychiatric medications. We have now inserted the sentence on line 114 - 116: “15 of the patients were on antidepressants, some co-medicated with either mood stabilizers or antipsychotics, the rest did not use any psychiatric medications.”

To define what actigraph worn day’s means, we have added the sentence “The Actigraph was worn continuously throughout the complete recording period.” (Line 128 – 129) in the Recording of motor activity part. We have furthermore improved the reporting on the actigraphy recordings. When reporting the average day’s actigraph recordings, we have supplemented the mean ± SD estimate with range (min – max). We have also updated the footnotes of tab. 1 and 4 to read, “1Number of 24-h sequences analyzed” for the Days1 variable, as well as reported the Days variable in table 3 and 6

A: It is true that the number of samples is small. To this extent, we employed a leave-one-out validation approach to make the most efficient use of the available data. This strategy also provides a better generalization estimate since it assumes that the model does not know anything about the target user, which is a common scenario in real life situations when one wants to use a system out-of-the-box without going into a calibration process.

#6. Please revise the figures and tables to make them readable. It is difficult to recognize.

A: Figures 1 and 2 are updated, but all tables are in line with PLOS ONEs requirements for tables, and according to instructions: “In Word, tables that run off of the manuscript page can be seen using Draft View.”

A: We totally agree with the reviewers’ comments on doing intra-individual comparisons of mood states, but we have yet not had access to such datasets. There have been identified differences between unipolar and bipolar patients when comparing shorter time series (especially in morning periods), but not in longer 24-h series, as stated in the manuscript. We agree that combining unipolar and bipolar depressions is a limitation of our analyzes, but the sample is too small to analyze by dividing the unipolar and bipolar patients.

#8. Statistics Line 188~

How did you deal with the section that could be thought of as sleep? Did you ever think about an activity level of zero throughout the day regardless of sleep or not?

A: As we have analyzed 24-h time series, we believe the proportion of Zero activity reflects both sleep patterns and active and non-active periods. Furthermore, the proportion of Zero probably mirrors reduced daytime motor-activity and less complexity in activity patterns typically associated with (retarded) depression.

#9. Outcome Metrics 197~

You mean a depressed condition? It would be better to describe it a little more clearly. Calling a condition group is easily confusing. It is recommended to describe it a depressed mood.

A: Thank you for identifying this unclear statement, the description is changed according to the recommendation. (Line 211)

#10. Table 1

A: We agree with the reviewer but assessment of MADRS was not done in the control group. This is a limitation that was pointed out in the manuscript (line 493 – 494 in the revised manuscript): “Anyhow, little is known about the control group beyond age, gender and the absence of a history of either affective or psychotic disorders.”

#11. When data related to sleep are analyzed together, some limitations of activity data can be improved. Consideration should be given to analyzing and presenting sleep data.

A: Depression is commonly associated with sleep disturbance, where some depressed people experience increased need for sleep, and others reduced sleep quality and less sleep duration. We chose to analyze a full 24-h time series incorporating sleep patterns. By doing it this way, we have followed the analytic recommendations from a systematic review on activation (Scott J., et al. Activation in bipolar disorders: A systematic review. JAMA Psychiatry. 2017).

A: Regarding utilizing secondary variables, the motivation behind applying CNN analyzing an image representation of the data, was to preserve all the information lost by the feature-extraction. Indeed, the image representation preserves all time series information. We added the following paragraph to the manuscript (line 185 – 189): “The motivation of using a CNN is because with this approach, more information is preserved as compared to a feature-based approach. With the CNN and the chosen representation, the granularity is at the minute level and there is no need to do feature extraction. On the other hand, for the non-CNN based methods, the features were computed on a daily basis which can lead to some information being lost”.

Furthermore, we have analyzed 24-h time series expressing a full circadian cycle, and do think diurnal variations of active and non-active periods and sleep patterns are incorporated. Although we principally agree with a need for addressing difference between weekdays and weekends in such data, we did not find this relevant for our sample, as our healthy controls are mainly shifts working hospital ward employees, working daytime, evenings and weekends, and we have no information about their work-schemes. The healthy control group is described in the previous papers on this sample. We have now added the sentence “The majority were shift working hospital staffs” at line 119.

The comprehensive analytical approach that the reviewer desires would require a self-reported systematic description of each individual's social rhythms. We agree that this would be a very expedient and interesting experiment, but should probably be done using intra-individual comparisons of various mood states. We have supplemented the manuscript with the following text (line 519 - 523). “ML analyzes in such an intra-individualistic sample, may provide analyzes beyond the 24-h circadian cycles studied in this experience. For instance, differences between morning and evening, active and non-active periods and sleep patterns, as well as activity differences between weekdays and weekends, could be more feasible in intra-individualistic samples”. Placed at the end of the paragraph discussing the need for intra-individualistic data on depression.

At the same time, we agree that additional features may provide more information to the predictive models. As suggested by the reviewer, it would be interesting to try additional data-driven approaches and feature engineering to extract more features related to weekdays, weekends, day and night patterns, etc. and perform a feature importance analysis to detect what are the most relevant variables when discriminating between classes. These types of analyses have been proposed as a future direction either by us or by other researchers since the dataset is public. We have added the following text in the discussion section (line 523 – 526): “In the present work, we have furthermore analyzed a possible set of statistical features extracted from activity time series, and displayed how accurate machine learning models can be trained with those. As a future direction, the utilized public dataset provides the possibility to explore the use of additional statistical features.”

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(38.7KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0231995.r003

Decision Letter 1

Kyoung-Sae Na

11 Aug 2020

Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls.

PONE-D-20-09443R1

Dear Dr. Jakobsen,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Kyoung-Sae Na, M.D.

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

**********

6. Review Comments to the Author

Reviewer #1: (No Response)

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Jonas Busk

PLoS One. doi: 10.1371/journal.pone.0231995.r004

Acceptance letter

Kyoung-Sae Na

14 Aug 2020

PONE-D-20-09443R1

Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls.

Dear Dr. Jakobsen:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Kyoung-Sae Na

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(38.7KB, docx)}

Data Availability Statement

The data can be accessed via: http://datasets.simula.no/depresjon/ Or directly downloaded from: https://doi.org/10.5281/zenodo.1219550.

[pone.0231995.ref001] 1.Bauer M, Andreassen OA, Geddes JR, Kessing LV, Lewitzka U, Schulze TG, et al. Areas of uncertainties and unmet needs in bipolar disorders: clinical and research perspectives. The Lancet Psychiatry 2018;5:930–39. 10.1016/S2215-0366(18)30253-0 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref002] 2.Scott J, Murray G, Henry C, Morken G, Scott E, Angst J, et al. Activation in bipolar disorders: A systematic review. JAMA Psychiatry. 2017;74(2):189–96. 10.1001/jamapsychiatry.2016.3459 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref003] 3.Burton C, McKinstry B, Szentagotai Tătar A, Serrano-Blanco A, Pagliari C, Wolters M. Activity monitoring in patients with depression: A systematic review. Journal of Affective Disorders. 2013;145(1):21–8. 10.1016/j.jad.2012.07.001 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref004] 4.Krane-Gartiser K, Henriksen T, Vaaler AE, Fasmer OB, Morken G. Actigraphically assessed activity in unipolar depression: a comparison of inpatients with and without motor retardation. Journal of clinical psychiatry. 2015;76(9):1181–7. 10.4088/JCP.14m09106 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref005] 5.Faedda GL, Marangoni C, Reginaldi D. Depressive mixed states: A reappraisal of Koukopoulos׳criteria. Journal of Affective Disorders. 2015;176:18–23. 10.1016/j.jad.2015.01.053 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref006] 6.Sabelli HC, Carlson-Sabelli L, Javaid JI. The thermodynamics of bipolarity: A bifurcation model of bipolar illness and bipolar character and its psychotherapeutic applications. Psychiatry. 1990;53(4):346–68. 10.1080/00332747.1990.11024519 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref007] 7.Dilsaver SC, Chen YR, Shoaib AM, Swann AC. Phenomenology of mania: evidence for distinct depressed, dysphoric, and euphoric presentations. American Journal of Psychiatry. 1999;156(3):426–30. 10.1176/ajp.156.3.426 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref008] 8.Tondo L, Vázquez GH, Pinna M, Vaccotto PA, Baldessarini RJ. Characteristics of depressive and bipolar disorder patients with mixed features. Acta Psychiat Scand. 2018;138(3):243–52. 10.1111/acps.12911 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref009] 9.Bourguignon C, Storch K-F. Control of Rest:Activity by a Dopaminergic Ultradian Oscillator and the Circadian Clock. Front. Neurol. 2017;8(614). [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref010] 10.Alloy LB, Ng TH, Titone MK, Boland EM. Circadian Rhythm Dysregulation in Bipolar Spectrum Disorders. Current Psychiatry Reports. 2017;19(4):21 10.1007/s11920-017-0772-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref011] 11.Glass L, Kaplan D. Time series analysis of complex dynamics in physiology and medicine. Medical progress through technology. 1993;19:115–. [PubMed] [Google Scholar]

[pone.0231995.ref012] 12.Fasmer EE, Fasmer OB, Berle JØ, Oedegaard KJ, Hauge ER. Graph theory applied to the analysis of motor activity in patients with schizophrenia and depression. PloS one. 2018;13(4):e0194791 10.1371/journal.pone.0194791 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref013] 13.Hauge ER, Berle JØ, Oedegaard KJ, Holsten F, Fasmer OB. Nonlinear analysis of motor activity shows differences between schizophrenia and depression: a study using Fourier analysis and sample entropy. PloS one. 2011;6(1):e16291 10.1371/journal.pone.0016291 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref014] 14.Scott J, Vaaler AE, Fasmer OB, Morken G, Krane-Gartiser K. A pilot study to determine whether combinations of objectively measured activity parameters can be used to differentiate between mixed states, mania, and bipolar depression. International Journal of Bipolar Disorders. 2017;5(1):5 10.1186/s40345-017-0076-6 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref015] 15.Pathak J, Wikner A, Fussell R, Chandra S, Hunt BR, Girvan M, et al. Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2018;28(4):041101. [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref016] 16.Wan ZY, Vlachas P, Koumoutsakos P, Sapsis T. Data-assisted reduced-order modeling of extreme events in complex dynamical systems. PloS one. 2018;13(5):e0197704 10.1371/journal.pone.0197704 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref017] 17.Valenza G, Nardelli M, Lanatà A, Gentili C, Bertschy G, Paradiso R, et al. Wearable Monitoring for Mood Recognition in Bipolar Disorder Based on History-Dependent Long-Term Heart Rate Variability Analysis. IEEE Journal of Biomedical and Health Informatics. 2014;18(5):1625–35. 10.1109/JBHI.2013.2290382 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref018] 18.Chang H-A, Chang C-C, Tzeng N-S, Kuo TBJ, Lu R-B, Huang S-Y. Heart rate variability in unmedicated patients with bipolar disorder in the manic phase. Psychiatry and Clinical Neurosciences. 2014;68(9):674–82. 10.1111/pcn.12178 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref019] 19.Fasmer OB, Liao H, Huang Y, Berle JØ, Wu J, Oedegaard KJ, et al. A naturalistic study of the effect of acupuncture on heart-rate variability. Journal of acupuncture and meridian studies. 2012;5(1):15–20. 10.1016/j.jams.2011.11.002 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref020] 20.Kolosnjaji B, Eckert C, editors. Neural network-based user-independent physical activity recognition for mobile devices. International Conference on Intelligent Data Engineering and Automated Learning; 2015: Springer.

[pone.0231995.ref021] 21.Inoue M, Inoue S, Nishida T. Deep recurrent neural network for mobile human activity recognition with high throughput. Artificial Life and Robotics. 2018;23(2):173–85. [Google Scholar]

[pone.0231995.ref022] 22.Ignatov A. Real-time human activity recognition from accelerometer data using Convolutional Neural Networks. Applied Soft Computing. 2018;62:915–22. [Google Scholar]

[pone.0231995.ref023] 23.Greff K, Srivastava RK, Koutník J, Steunebrink BR, Schmidhuber J. LSTM: A search space odyssey. IEEE transactions on neural networks and learning systems. 2017;28(10):2222–32. 10.1109/TNNLS.2016.2582924 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref024] 24.Marblestone AH, Wayne G, Kording KP. Toward an integration of deep learning and neuroscience. Frontiers in Computational Neuroscience. 2016;10:94 10.3389/fncom.2016.00094 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref025] 25.Ribeiro MT, Singh S, Guestrin C. "Why Should I Trust You?": Explaining the Predictions of Any Classifier. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; San Francisco, California, USA. 2939778: ACM; 2016. p. 1135–44.

[pone.0231995.ref026] 26.Bzdok D, Ioannidis JPA. Exploration, Inference, and Prediction in Neuroscience and Biomedicine. Trends in Neurosciences. 2019. [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref027] 27.Huys QJM, Maia TV, Frank MJ. Computational psychiatry as a bridge from neuroscience to clinical applications. Nat Neurosci. 2016;19(3):404–13. 10.1038/nn.4238 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref028] 28.Liaw A, Wiener M. Classification and regression by randomForest. R news. 2002;2(3):18–22. [Google Scholar]

[pone.0231995.ref029] 29.Molnar C. Interpretable machine learning: A guide for making black box models explainable. https://christophm.github.io/interpretable-ml-book2018. Available from: https://leanpub.com/interpretable-machine-learning.

[pone.0231995.ref030] 30.Berle JO, Hauge ER, Oedegaard KJ, Holsten F, Fasmer OB. Actigraphic registration of motor activity reveals a more structured behavioural pattern in schizophrenia than in major depression. BMC Research Notes. 2010;3:149–. 10.1186/1756-0500-3-149 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref031] 31.American Psychiatric Association. Diagnostic and statistical manual of mental disorders (4th ed.). Washington DC: American Psychiatric Press; 1994. [Google Scholar]

[pone.0231995.ref032] 32.Montgomery S, Asberg A. A new depression scale designed to be sensitive to change. Br J Psychiat. 1979;134. [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref033] 33.Garcia-Ceja E, Riegler M, Jakobsen P, Tørresen J, Nordgreen T, Oedegaard KJ, et al., editors. Depresjon: a motor activity database of depression episodes in unipolar and bipolar patients. Proceedings of the 9th ACM Multimedia Systems Conference; 2018. 10.1145/3204949.3208125:ACM [DOI]

[pone.0231995.ref034] 34.Garcia-Ceja E, Riegler M, Jakobsen P, Torresen J, Nordgreen T, Oedegaard KJ, et al. , editors. Motor Activity Based Classification of Depression in Unipolar and Bipolar Patients. 2018 IEEE 31st International Symposium on Computer-Based Medical Systems (CBMS); 2018: IEEE. [Google Scholar]

[pone.0231995.ref035] 35.Garcia-Ceja E, Osmani V, Mayora O. Automatic Stress Detection in Working Environments From Smartphones’ Accelerometer Data: A First Step. IEEE Journal of Biomedical and Health Informatics. 2016;20(4):1053–60. 10.1109/JBHI.2015.2446195 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref036] 36.Riegler M, Lux M, Griwodz C, Spampinato C, de Lange T, Eskeland SL, et al., editors. Multimedia and medicine: Teammates for better disease detection and survival. Proceedings of the 24th ACM international conference on Multimedia; 2016: ACM.

[pone.0231995.ref037] 37.Kotsiantis S, Kanellopoulos D, Pintelas P. Handling imbalanced datasets: A review. GESTS International Transactions on Computer Science and Engineering. 2006;30(1):25–36. [Google Scholar]

[pone.0231995.ref038] 38.Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research. 2002;16:321–57. [Google Scholar]

[pone.0231995.ref039] 39.Breiman L. Random Forests. Machine Learning. 2001;45(1):5–32. [Google Scholar]

[pone.0231995.ref040] 40.LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998;86(11):2278–324. [Google Scholar]

[pone.0231995.ref041] 41.Nabih-Ali M, El-Dahshan ELSA, Yahia AS. A review of intelligent systems for heart sound signal analysis. Journal of Medical Engineering & Technology. 2017;41(7):553–63. [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref042] 42.Garcia-Ceja E, Brena R, Carrasco-Jimenez J, Garrido L. Long-term activity recognition from wristwatch accelerometer data. Sensors 2014;14(12):22500–24. 10.3390/s141222500 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref043] 43.Pepe MS. The statistical evaluation of medical tests for classification and prediction. Oxford: Medicine; 2003. [Google Scholar]

[pone.0231995.ref044] 44.Boughorbel S, Jarray F, El-Anbari M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PloS one. 2017;12(6):e0177678 10.1371/journal.pone.0177678 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref045] 45.Friedman JH. Greedy function approximation: a gradient boosting machine. Annals of statistics. 2001:1189–232. [Google Scholar]

[pone.0231995.ref046] 46.Greenwell BM. pdp: an R Package for constructing partial dependence plots. The R Journal. 2017;9(1):421–36. [Google Scholar]

[pone.0231995.ref047] 47.Fleiss JL, Bigger JT Jr, Rolnitzky LM. The correlation between heart period variability and mean period length. Statistics in Medicine. 1992;11(1):125–9. 10.1002/sim.4780110111 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref048] 48.Krane-Gartiser K, Henriksen TEG, Morken G, Vaaler A, Fasmer OB. Actigraphic assessment of motor activity in acutely admitted inpatients with bipolar disorder. PloS one. 2014;9(2):e89574 10.1371/journal.pone.0089574 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref049] 49.Krane-Gartiser K, Vaaler AE, Fasmer OB, Sørensen K, Morken G, Scott J. Variability of activity patterns across mood disorders and time of day. BMC psychiatry. 2017;17(1):404–. 10.1186/s12888-017-1574-x [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref050] 50.Oedegaard KJ, Neckelmann D, Fasmer OB. Type A behaviour differentiates bipolar II from unipolar depressed patients. Journal of Affective Disorders. 2006;90(1):7–13. 10.1016/j.jad.2005.10.005 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref051] 51.Pirkola S, Eriksen HA, Partonen T, Kieseppä T, Veijola J, Jääskeläinen E, et al. Seasonal variation in affective and other clinical symptoms among high-risk families for bipolar disorders in an Arctic population. International journal of circumpolar health. 2015;74(1):29671. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0231995.ref052] 52.De Crescenzo F, Economou A, Sharpley AL, Gormez A, Quested DJ. Actigraphic features of bipolar disorder: A systematic review and meta-analysis. Sleep Med Rev. 2017;33:58–69. 10.1016/j.smrv.2016.05.003 [DOI] [PubMed] [Google Scholar]

[pone.0231995.ref053] 53.Krane-Gartiser K, Asheim A, Fasmer OB, Morken G, Vaaler AE, Scott J. Actigraphy as an objective intra-individual marker of activity patterns in acute-phase bipolar disorder: a case series. International journal of bipolar disorders. 2018;6(1):8–. 10.1186/s40345-017-0115-3 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Applying machine learning in motor activity time series of depressed bipolar and unipolar patients compared to healthy controls

Petter Jakobsen

Enrique Garcia-Ceja

Michael Riegler

Lena Antonsen Stabell

Tine Nordgreen

Jim Torresen

Ole Bernt Fasmer

Ketil Joachim Oedegaard

Roles

Abstract

Introduction

Materials and methods

Sample characteristics

Recording of motor activity

Machine learning

Statistics

Outcome metrics

Results

Table 1. Characteristics of the depressed patients and healthy controls analyzed in the first machine learning run.

Table 2. Machine learning classification results (1st run) in motor activity time series from depressed patients (n = 23) and healthy controls (n = 32).

Fig 1. Model interpretability analysis (1st run).

Table 3. Characteristics of classification results by predicted condition from the 1st machine learning run.

Table 4. Characteristics of depressed patients and healthy controls analyzed in the 2nd machine learning run.

Table 5. Machine learning classification results (2nd run) in motor activity time series of motor retarded depressed patients (n = 17) and healthy controls (n = 32).

Table 6. Characteristics of classification results by predicted condition from the second machine learning run.

Fig 2. Model interpretability analysis (2nd run).

Discussion

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Kyoung-Sae Na

Roles

Author response to Decision Letter 0

Decision Letter 1

Kyoung-Sae Na

Roles

Acceptance letter

Kyoung-Sae Na

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases