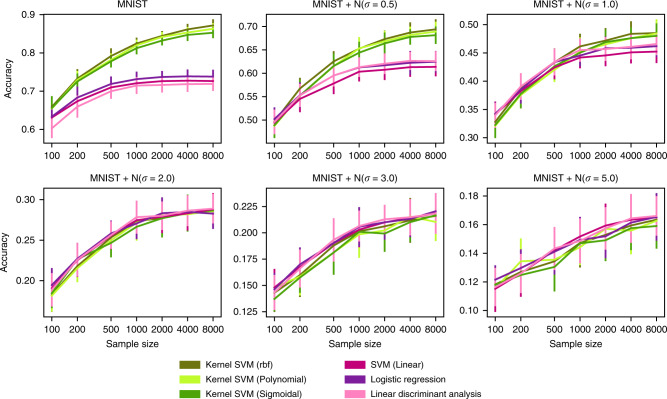
Fig. 6. Adding noise to MNIST images leads to scaling behavior similar to that of brain images.

We extracted the eight leading principal components from the digit images (MNIST) and added Gaussian noise to each principal component. The principal component embeddings were then used as input variables for the models (see Supplementary Information for details) to predict the class label (i.e., digits). Increasing the amount of noise from σ = 0.5 up to σ = 5.0 entailed two effects: first, gradual diminishing of the performance difference between nonlinear kernel models and linear models. Second, the increasing level of noise in the images reduced the extent to which prediction performance saturated with increasing sample size. At σ = 5.0, the sample complexity curves of MNIST data followed the same pattern as we observed on brain images (Fig. 2): kernel and linear models performed indistinguishably, and prediction performance did not visibly saturate. Our quantitative findings invite the tentative speculation that MRI brain-imaging data may be too noisy to allow capturing nonlinear relationships for phenotype prediction at currently available sample sizes. Error bars = mean ± 1 SD across 20 cross-validation iterations (all panels).