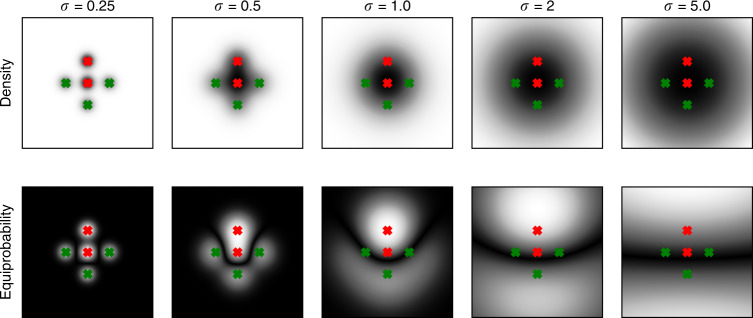
Fig. 7. Gaussian noise can lead to linearization of decision boundaries.

Shows a simple nonlinear binary classification problem consisting of two mixtures of Gaussians in 2D space with identical isotropic covariance (σ). Samples of the first class are generated by the two Gaussians marked with red crosses; samples of the second class are generated by the three Gaussians marked with green crosses. The first row indicates the overall probability density for the generating mixtures. The second row indicates equiprobability—i.e., f(x, y) = |P_red(x, y) − P_green(x, y)|—areas in which both red and green classes are equally likely (black). The resulting black margin separating the red and green mixtures represents the ideal decision boundary. Adding Gaussian noise—i.e., increasing σ—gradually turns the decision boundary from a highly nonlinear U-shape (σ < 2) to a linear decision boundary (σ > 2). Hence, in certain data scenarios, high levels of Gaussian noise can linearize an irregular decision boundary.