Model-based clustering of time-evolving networks through temporal exponential-family random graph models

Abstract

Dynamic networks are a general language for describing time-evolving complex systems, and discrete time network models provide an emerging statistical technique for various applications. It is a fundamental research question to detect a set of nodes sharing similar connectivity patterns in time-evolving networks. Our work is primarily motivated by detecting groups based on interesting features of the time-evolving networks (e.g., stability). In this work, we propose a model-based clustering framework for time-evolving networks based on discrete time exponential-family random graph models, which simultaneously allows both modeling and detecting group structure. To choose the number of groups, we use the conditional likelihood to construct an effective model selection criterion. Furthermore, we propose an efficient variational expectation-maximization (EM) algorithm to find approximate maximum likelihood estimates of network parameters and mixing proportions. The power of our method is demonstrated in simulation studies and empirical applications to international trade networks and the collaboration networks of a large research university.

1. Introduction

Dynamic networks are a general language for describing time-evolving complex systems, and discrete time network models provide an emerging statistical technique to study biological, business, economic, information, and social systems. For example, time-evolving networks shed light on understanding critical processes such as the study of biological functions using protein-protein interaction networks [14, 40], and also contribute to assessing infectious disease epidemiology and time-evolving structures of social networks [6, 25, 32].

A group can be defined as a set of nodes sharing similar connectivity patterns. In computer science and statistical physics, many node clustering algorithms have been developed. Girvan and Newman [13] propose an algorithm to identify groups based on edge “betweenness”. They construct groups by progressively removing the edges that connect groups most from the original network. Newman and Girvan [34] proposed three different measures of “betweenness” and compared the results based on modularity, which measures the quality of a particular division of a network. On the other hand, in statistics, analyzing and clustering networks are often based on statistical mixture models. One idea of model-based clustering in networks comes from Handcock et al. [15], who propose a latent position cluster model that extends the latent space model of Hoff et al. [18] to take account of clustering, using the model-based clustering ideas of Fraley and Raftery [12]. In the current literature, there are two very popular statistical modeling frameworks. One is the stochastic blockmodel (SBM), and the other is the exponential-family random graph model (ERGM).

Stochastic blockmodels were first introduced by Holland et al. [19], and they focused on the case of a priori specified blocks, where the memberships are known or assumed, and the goal is to estimate a matrix of edge probabilities. A statistical approach to a posteriori block modeling for networks was introduced by Snijders and Nowicki [38] and Nowicki and Snijders [35], where the objective is to estimate the matrix of edge probabilities and the memberships simultaneously. Airoldi et al. [2] relax the assumption of a single latent role for nodes and develop a mixed membership stochastic blockmodel. Karrer and Newman [22] relax the assumption that a stochastic blockmodel treats all nodes within a group as stochastically equivalent and proposes a degree-corrected stochastic blockmodel. Moreover, in recent years, asymptotic theory of these models has been advanced by Bickel and Chen [8], Choi et al. [9], Amini et al. [5], and others. A group, or community, in a stochastic blockmodel is defined as a set of nodes with more edges amongst its nodes than between its nodes. The communities are interpreted meaningfully in many research fields. For example, in citation and collaboration networks, such communities can be interpreted as scientific disciplines [21, 33]. Communities in food web networks can be interpreted as ecological subsystems [13].

As dynamic network analysis has become an emergent scientific field, there has been a growing number of dynamic network models in the stochastic blockmodel framework. Yang et al. [49] propose a model that captures the evolution of communities with fixed connectivity parameters. Xu and Hero [47] and Matias and Miele [31] propose methods that allow both community memberships and connectivity parameters to vary over time. Xing et al. [46] and Ho et al. [17] propose dynamic extensions of the mixed membership stochastic blockmodel using a state space model. More details about recent statistical methods for dynamic networks with latent variables can be found in a recent survey [23].

Different from the stochastic blockmodel framework, exponential-family random graph models allow researchers to incorporate interesting features of the network into models. Researchers can specify a model capturing those features and cluster nodes based on the specified model. Indeed, the stochastic blockmodel is a special case of a mixture of exponential-family random graph models. Some estimation algorithms for exponential-family random graph models do not scale well computationally to large networks. Vu et al. [42] propose ERGM-based clustering for large-scale cross-sectional networks that solves the scalability issue by assuming dyadic independence conditional on the group memberships of nodes. Agarwal and Xue [1] propose ERGM-based clustering to study large-scale weighted networks. In recent years, several authors also have proposed discrete time network models based on ERGM. Hanneke et al. [16] propose a temporal ERGM (TERGM) to fit the model to a network series and Krivitsky and Handcock [26] propose a separable temporal ERGM (STERGM) that gives more flexibility in modeling time-evolving networks.

Our work is primarily motivated by detecting groups based on interesting features of time-evolving networks, and our results advance existing literature by introducing a promising framework that incorporates model-based clustering while remaining computationally scalable for time-evolving networks. This framework is based on discrete time exponential-family random graph models and inherits the philosophy of finite mixture models, which simultaneously allows both modeling and detecting groups in time-evolving networks. The groups can be defined differently based on how researchers and practitioners incorporate interesting features of the time-evolving networks into the models. For example, in sociology, researchers are interested in whether, say, same-gender friendships are more stable than other friendships or whether there are differences among ethnic categories in forming lasting sexual partnerships over time [24, 28]. In this case, stability parameters can be incorporated into the model, resulting in different groups of nodes with different degrees of stability. We also propose an efficient variational expectation-maximization (EM) algorithm that exhibits computational scalability for time-evolving networks by exploiting variational methods and minorization-maximization (MM) techniques. Moreover, we propose a conditional likelihood Bayesian information criterion to solve the model selection problem of determining an appropriate number of groups.

The rest of this paper is organized as follows. In Section 2, we present our model-based clustering method for time-evolving networks based on a finite mixture of discrete time exponential-family random graph models. Section 3 designs an efficient variational expectation-maximization algorithm to find approximate maximum likelihood estimates of network parameters and mixing proportions. Given these estimates, we can infer membership labels and solve the problem of detecting groups for time-evolving networks. In Section 4, we use conditional likelihood to construct an effective model selection criterion. The power of our method is demonstrated by simulation studies in Section 5 and real-world applications to international trade networks and collaboration networks in Section 6. Section 7 includes a few concluding remarks. Proofs and technical details are provided in appendix and the supplementary file.

2. Methodology

2.1. Model-based clustering of time-evolving networks

We present the model-based clustering for time-evolving networks based on a finite mixture of discrete time exponential-family random graph models. First, we introduce the necessary notation. Let n nodes be fixed over time and indexed by 1, …, n. Let ${\mathbf{Y}}_t={\left\{Y_{t,ij}\right\}}_{1\le i,j\le n}\in \mathcal{Y}$ represent a random binary network at time t ∈ {0, …, T} and denote by y_t = {y_{t,i j}}_{1≤i, j≤n} the corresponding observed network, where $\mathcal{Y}$ is the set of all possible networks. Let $\mathit{\theta }\in {ℝ}^p$ be a vector of p network parameters of interest. Under the kth-order Markov assumption, discrete time exponential-family random graph models are of the form

$$\mathrm{Pr}\left({\mathbf{Y}}_t={\mathbf{y}}_t|{\mathbf{y}}_{t-1},\dots ,{\mathbf{y}}_0\right)=\exp \left\{{\mathit{\theta }}^{\top }\mathit{g}\left({\mathbf{y}}_t,\dots ,{\mathbf{y}}_{t-k}\right)-\psi \left(\mathit{\theta },{\mathbf{y}}_{t-1},\dots ,{\mathbf{y}}_{t-k}\right)\right\},$$

where $\psi \left(\mathit{\theta },{\mathbf{y}}_{t-1},\dots ,{\mathbf{y}}_{t-k}\right)=\ln {\sum }_{{\mathbf{y}}^{*}\in \mathcal{Y}}\exp \left\{{\mathit{\theta }}^{\top }\mathit{g}\left({\mathbf{y}}^{*},{\mathbf{y}}_{t-1},\dots ,{\mathbf{y}}_{t-k}\right)\right\}$ ensuring that Pr(Y_t = y_t | y_t−1, …, y₀) sums to 1. Here, g(y_t, …, y_t−k) is a p-dimensional vector of sufficient statistics on networks y_t, …, y_t−k.

We now focus on the simplest case of discrete time exponential-family random graph models under the first-order Markov assumption and we write the one-step transition probability from Y_t−1 to Y_t as

$$\mathrm{Pr}\left({\mathbf{Y}}_t={\mathbf{y}}_t|{\mathbf{y}}_{t-1}\right)=\exp \left\{{\mathit{\theta }}^{\top }\mathit{g}\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)-\psi \left(\mathit{\theta },{\mathbf{y}}_{t-1}\right)\right\},$$ (1)

where ψ(θ, y_t−1) and g(y_t, y_t−1) are defined as above.

Remark 1: Given covariates x_t and a vector $\mathit{\beta }\in {ℝ}^q$ of covariate coefficients, we can also write the transition probability from Y_t−1 to Y_t with covariates as

$$\mathrm{Pr}\left({\mathbf{Y}}_t={\mathbf{y}}_t|{\mathbf{y}}_{t-1},{\mathbf{x}}_t\right)=\exp \left\{{\mathit{\theta }}^{\top }\mathit{g}\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)+{\mathit{\beta }}^{\top }\mathit{h}\left({\mathbf{y}}_t,{\mathbf{x}}_t\right)-\psi \left(\mathit{\theta },\mathit{\beta },{\mathbf{y}}_{t-1}\right)\right\},$$

where h(y_t, x_t) is a q-dimensional vector of statistics and $\psi \left(\mathit{\theta },\mathit{\beta },{\mathbf{y}}_{t-1}\right)=\ln {\sum }_{{\mathbf{y}}^{*}\in \mathcal{Y}}\exp \left\{{\mathit{\theta }}^{\top }\mathit{g}\left({\mathbf{y}}^{*},{\mathbf{y}}_{t-1}\right)+{\mathit{\beta }}^{\top }\mathit{h}\left({\mathbf{y}}^{*},{\mathbf{x}}_t\right)\right\}$.

In general, for some choices of g(y_t, y_t−1), the model in (1) is not tractable for modeling large networks, since the computing time to evaluate the likelihood function directly grows as $2^{\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)}$ in the case of undirected edges. Here, we restrict our attention to scalable exponential-family models by only choosing statistics that preserve dyadic independence wherein the distribution of Y_t given Y_t−1 factors over the edge states Y_t,ij given the previous time point edge states Y_t−1,ij, i.e.,

$$\mathrm{Pr}\left({\mathbf{Y}}_t={\mathbf{y}}_t|{\mathbf{y}}_{t-1}\right)=\prod _{i<j}^n\mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij}\right).$$ (2)

For example, we may consider the following statistics that preserve dyadic independence and capture interesting time-evolving network features in both TERGM and STERGM:

$$g^d\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)=\sum _{i<j}^n{y}_{t,ij},$$ (3)

$$g^s\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)=\sum _{i<j}^n\left\{y_{t,ij}{y}_{t-1,ij}+\left(1-y_{t,ij}\right)\left(1-y_{t-1,ij}\right)\right\},$$ (4)

$$g^f\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)=\sum _{i<j}^n\left(y_{t,ij}-y_{t,ij}{y}_{t-1,ij}\right),$$ (5)

$$g^p\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)=\sum _{i<j}^n{y}_{t,ij}{y}_{t-1,ij}.$$ (6)

The subscripted i < j and superscripted n mean that summation should be taken over all pairs (i, j) with 1 ≤ i ≤ j ≤ n; the same is true for products as in equation (2). Corresponding to the first and second statistics above are TERGM parameters: θ^d relates to density, or the number of edges in the network at time t, while θ^s relates to stability, or the number of edges maintaining their status from time t − 1 to time t. Corresponding to the third and fourth statistics above are STERGM parameters: θ^f relates to formation, or the number of edges absent at time t − 1 but present at time t, while θ^p relates to persistence, or the number of edges existing at time t − 1 that survive to time t.

Remark 2: We can extend the proposed model to handle directed binary networks by considering statistics that preserve dyadic independence and capture directed features of the network. For example, we can consider the TERGM statistics $g^r\left({\mathbf{y}}_t,{\mathbf{y}}_{t-1}\right)={\sum }_{i,j}^n{y}_{t,ij}{y}_{t-1,ji}$, which represent reciprocity. The subscripted i, j and superscripted n mean that summation should be taken over all pairs (i, j) with 1 ≤ i ≠ j ≤ n.

Here, as in Vu et al. [42], we assume that the joint probability mass function, given an initial network y₀, has a K-component mixture form as follows:

$$\begin{gathered} \mathrm{Pr}\left({\mathbf{y}}_1,\dots ,{\mathbf{y}}_T|{\mathbf{y}}_0\right)=\sum _{z\in \mathcal{Z}}\left\{\mathrm{Pr}\left(\mathit{Z}=z|{\mathbf{y}}_0\right)\prod _{t=1}^T\mathrm{Pr}\left({\mathbf{Y}}_t={\mathbf{y}}_t|{\mathbf{y}}_{t-1},z\right)\right\} \\ =\sum _{z\in \mathcal{Z}}\left\{\mathrm{Pr}\left(\mathit{Z}=z|{\mathbf{y}}_0\right)\prod _{t=1}^T\prod _{i<j}^n\mathrm{Pr}\left(Y_{t,i}{}_j=y_{t,ij}|y_{t-1,ij},z\right)\right\}, \end{gathered}$$ (7)

where Z = (Z₁, …, Z_n) denotes the membership indicators that follow the following multinomial distributions

$${\mathit{Z}}_i|{\pi }_1,\dots ,{\pi }_K\stackrel{\text{i.i.d.}}{\sim }\text{Multinomial}\left(1;{\pi }_1,\dots ,{\pi }_K\right),$$

and $\mathcal{Z}$ denotes the support of the membership indicators Z. In the mixture form (7), the assumption of conditional dyadic independence given z strikes a balance between model complexity and parsimony because it allows for marginal dyadic dependence and it means nodes in the same group share the same model parameters. For now, the number of groups K is fixed and known. In Section 4, we will discuss how to choose an optimal number of groups K.

Now, we observe a series of networks, y₁, …, y_T, given an initial network y₀. The log-likelihood of the observed network series is

$$\ell (\pi ,\mathit{\theta })=\ln \left[\sum _{z\in \mathcal{Z}}\left\{\mathrm{Pr}\left(\mathit{Z}=z|{\mathbf{y}}_0\right)\prod _{t=1}^T\mathrm{Pr}\left({\mathbf{Y}}_t={\mathbf{y}}_t|{\mathbf{y}}_{t-1},z\right)\right\}\right].$$

Our aim is to estimate π and θ via maximizing the log-likelihood ℓ(π, θ), i.e.,

$$(\widehat{\pi },\widehat{\mathit{\theta }})=\underset{(\pi ,\mathit{\theta })}{\arg \max }\ell (\pi ,\mathit{\theta }).$$

However, directly maximizing the log-likelihood function is computationally intractable since it is a sum over all possible latent block structures. Hence, in Section 3, we design a novel variational EM algorithm to efficiently find the approximate maximum likelihood estimates. We shall see that the parameter estimates obtained by this algorithm can provide group membership labels.

Before proceeding, we give specific examples of discrete time exponential-family random graph models with stability parameter(s) that control the rate of evolution of a network.

Example 1: The model in (7) takes the following form when g(y_t, y_t−1) consists only of the stability parameters (4) and when node i belongs to group k and node j belongs to group l:

$$\mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij},z\right)\propto \exp \left\{\left({\theta }_k^s+{\theta }_l^s\right)\left(y_{t,ij}{y}_{t-1,ij}+\left(1-y_{t,ij}\right)\left(1-y_{t-1,ij}\right)\right)\right\}.$$

Example 2: The model in (7) takes the following form when g(y_t, y_t−1) consists of both formation parameters (5) and persistence parameters (6) and when node i belongs to group k and node j belongs to group l:

$$\mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij},z\right)\propto \exp \{({\theta }_k^f+{\theta }_l^f)\left(y_{t,ij}-y_{t,ij}{y}_{t-1,ij}\right)+\left({\theta }_k^p+{\theta }_l^p\right)y_{t,ij}{y}_{t-1,ij}\}.$$

Remark 3: When K = 1, Example 1 reduces to TERGM with a stability parameter as in Hanneke et al. [16] and the model in Example 2 reduces to STERGM with formation and persistence parameters as in Krivitsky and Handcock [26].

2.2. Parameter identifiability

Parameter identifiability is essential to avoid inconsistent parameter estimation results among different methods. The unique identifiability of the parameters in a broad class of random graph mixture models has been shown by Allman et al. [3, 4]. Here we prove generic identifiability for our proposed discrete time exponential-family random graph mixture model where the distribution of Y_t given Y_t−1 is factorized as in equation (2). Theorem 1, whose proof is given in appendix, extends the identifiability result of the stochastic blockmodel of Allman et al. [3, 4] to discrete time exponential-family random graph mixture models. In this context, “generically identifiable” means the set of all uniquely identifiable parameters has a complement of Lebesgue measure zero in the full parameter space.

Theorem 1. Suppose a time-evolving network on n nodes is first-order Markov and has the form given in equation (2). The parameters π_k, 1 ≤ k ≤ K, and p_kl = Pr(Y_t,ij = 1 | y_t-1,_ij, Z_ik = Z_jl = 1), 1 ≤ k ≤ l ≤ K, are generically identifiable from the joint distribution of Y₁,..., Y_T, given an initial network y₀, up to permutations of the subscripts 1,..., K, if

$$\{\begin{array}{ll}\sqrt{n}\ge 4,\hfill & forK=2;\hfill \\ \sqrt{n}\ge K-1+\frac{{(K+2)}^2}{4},\hfill & forKeven,K\ge 4;\hfill \\ \sqrt{n}\ge K-1+\frac{(K+1)(K+3)}{4},\hfill & forKodd.\hfill \end{array}$$

Moreover, when the model also takes the exponential-family form (1), the network parameters ${\mathit{\theta }}_k\in {ℝ}^p$, 1 ≤ k ≤ K are generically identifiable, up to permutations of the subscripts 1, …, K, if the corresponding network statistics are not linearly dependent and p ≤ ⌊(K + 1)/2⌋ where ⌊·⌋ is a floor function that maps the given value to the largest integer less than or equal to it.

3. Computation

We present a novel variational EM algorithm to solve model-based clustering for time-evolving networks. Our algorithm is based on the algorithm presented by Vu et al. [42]. The algorithm combines the power of variational methods [43] and minorization-maximization techniques [20] to effectively handle both the computationally intractable log-likelihood function ℓ(π, θ) and the non-convex optimization problem of the lower bound of the log-likelihood. We introduce an auxiliary distribution A(z) ≡ Pr(Z = z) to derive a tractable lower bound on the intractable log-likelihood function. Using Jensen’s inequality, the log-likelihood function may be shown to be bounded from below as follows:

$$\ln \mathrm{Pr}\left({\mathbf{y}}_1,\dots ,{\mathbf{y}}_T|{\mathbf{y}}_0\right)=\ln \left\{\sum _{z\in \mathcal{Z}}\frac{\mathrm{Pr}\left({\mathbf{y}}_1,\dots ,{\mathbf{y}}_T,z|{\mathbf{y}}_0\right)}{A(z)}A(z)\right\}\ge \sum _{z\in \mathcal{Z}}\left\{\ln \frac{\mathrm{Pr}\left({\mathbf{y}}_1,\dots ,{\mathbf{y}}_T,z|{\mathbf{y}}_0\right)}{A(z)}\right\}A(z).$$ (8)

We would obtain the best lower bound when A(z) is given by Pr(Z = z | y_T,…, y₀), where the inequality becomes equality. However, this form of A(z) is computationally intractable since it cannot be further factored over nodes. We therefore constrain A(z) to a subset of tractable choices and maximize the tractable lower bound to find approximate maximum likelihood estimates.

Here, we constrain A(z) to the mean-field variational family where the Z_i are mutually independent, i.e., $A(z)={\prod }_{i=1}^n\mathrm{Pr}\left(Z_i=z_i\right)$. We further specif Pr(Z_i = z_i) to be Multinomial(1; γ_i1,…,γ_iK) for i ∈ {1,…, n}, where Γ = (γ₁, …, γ_n) is the variational parameter. In the estimation phase, whenever it is necessary to assign each node to a particular group, the ith node is assigned to the group with the highest value among ${\widehat{\gamma }}_{i1},\dots ,{\widehat{\gamma }}_{iK}$.

If we denote the right side of (8) by LB(π, θ; Γ), we may write

$$\mathrm{LB}(\mathit{\pi },\mathit{\theta };\mathbf{\Gamma })=\sum _{t=1}^T\sum _{i<j}^n\sum _{k=1}^K\sum _{l=1}^K{\gamma }_{ik}{\gamma }_{jl}\ln \mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij},Z_{ik}=Z_{jl}=1\right)+\sum _{i=1}^n\sum _{k=1}^K{\gamma }_{ik}\left(\ln {\pi }_k-\ln {\gamma }_{ik}\right).$$ (9)

Additional details on obtaining the lower bound are presented in the supplementary file. If π^(τ), θ^(τ), and Γ^(τ) denote the parameter estimates at the τth iteration of our variational EM algorithm, the algorithm alternates between

• Idealized Variational M-step:

  Let Γ^(τ+1) = arg max_Γ LB(π^(τ), θ^(τ); Γ).

• Variational M-step:

  Let(π^(τ+1), θ^(τ+1)) = arg max_{(π, θ)}LB(π, θ; Γ^(τ+1))

In the idealized variational E-step, it is difficult to directly maximize the nonconcave function LBLB(π^(τ), θ^(τ); Γ) with respect to Γ. To address this challenge, we use a minorization-maximization technique to construct a tractable minorizing function of LB(π^(τ), θ^(τ); Γ), then maximize this minorizer. Define

$$\begin{gathered} Q\left({\mathit{\pi }}^{(\tau )},{\mathbf{\theta }}^{(\tau )},{\mathbf{\Gamma }}^{(\tau )};\mathbf{\Gamma }\right)=\sum _{t=1}^T\sum _{i<j}^n\sum _{k=1}^K\sum _{l=1}^K\left({\gamma }_{ik}^2\frac{{\gamma }_{jl}^{(\tau )}}{2{\gamma }_{ik}^{(\tau )}}+{\gamma }_{jl}^2\frac{{\gamma }_{ik}^{(\tau )}}{2{\gamma }_{jl}^{(\tau )}}\right)\ln \mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij},Z_{ik}=Z_{jl}=1\right) \\ +\sum _{i=1}^n\sum _{k=1}^K{\gamma }_{ik}\left(\ln {\pi }_k^{(\tau )}-\ln {\gamma }_{ik}^{(\tau )}-\frac{{\gamma }_{ik}}{{\gamma }_{ik}^{(\tau )}}+1\right), \end{gathered}$$ (10)

which satisfies the defining characteristics of a minorizing function, namely for all Γ,

$$Q\left({\mathit{\pi }}^{(\tau )},{\mathbf{\theta }}^{(\tau )},{\mathbf{\Gamma }}^{(\tau )};\mathbf{\Gamma }\right)\le \mathrm{LB}\left({\mathbf{\pi }}^{(\tau )},{\mathbf{\theta }}^{(\tau )};\mathbf{\Gamma }\right)$$ (11)

and

$$Q\left({\mathit{\pi }}^{(\tau )},{\mathbf{\theta }}^{(\tau )},{\mathbf{\Gamma }}^{(\tau )};{\mathbf{\Gamma }}^{(\tau )}\right)\le \mathrm{LB}\left({\mathbf{\pi }}^{(\tau )},{\mathbf{\theta }}^{(\tau )};{\mathbf{\Gamma }}^{(\tau )}\right).$$ (12)

Additional details on constructing this minorizing function are presented in the supplementary material. Since (10) is concave in Γ and separates into functions of the individual γ_ik parameters, maximizing (10) is equivalent to solving a sequence of constrained quadratic programming subproblems with respect to γ₁,…,γ_n respectively, under constraints γ_i1,…,γ_iK ≥ 0 and ${\sum }_{k=1}^K{\gamma }_{ik}=1$ for i ∈ {1,…, n}.

To maximize LB(π, θ; Γ^(τ+1)) in the variational M-step, maximization with respect to π and θ may be accomplished separately. First, to derive the closed-form update for π, we introduce a Lagrange multiplier with the constraint ${\sum }_{k=1}^K{\pi }_k=1$, which yields

$${\pi }_k^{(\tau +1)}=\frac{1}{n}\sum _{i=1}^n{\gamma }_{ik}^{(\tau +1)},k\in \{1,\dots ,K\}.$$

We could obtain θ^(τ+1) using the Newton-Raphson method, though naive application of Newton-Raphson will not guarantee an increase in (9), which is necessary for the ascent property of the lower bound of the log-likelihood. Since the Hessian matrix H(θ^(τ)) at the τth iteration is positive definite, it can be shown that if θ moves in the direction $h^{(\tau )}=-H{\left({\mathit{\theta }}^{(\tau )}\right)}^{-1}\nabla \text{L}B\left({\mathit{\theta }}^{(\tau )};{\mathbf{\Gamma }}^{(\tau +1)}\right)$ of the Newton-Raphson method, the LB(·) function is guaranteed to increase initially. In our modified Newton-Raphson method we do not find the successor point θ^(τ+1) = θ^(τ) + h^(τ) as in the standard Newton-Raphson method. We instead take h^(τ) as a search direction and perform a line search [7] to find ${\lambda }^{*}=\arg {\max }_{\lambda \in (0,1]}\mathrm{LB}\left({\mathit{\theta }}^{(\tau )}+\lambda h^{(\tau )};{\mathbf{\Gamma }}^{(\tau +1)}\right)$, then we find the successor point θ^(τ+1) by

$${\mathit{\theta }}^{(\tau +1)}={\mathit{\theta }}^{(\tau )}-{\lambda }^{*}H{\left({\mathit{\theta }}^{(\tau )}\right)}^{-1}\nabla \mathrm{LB}\left({\mathit{\theta }}^{(\tau )};{\mathbf{\Gamma }}^{(\tau +1)}\right).$$ (13)

In Algorithm 1, we summarize the proposed variational EM algorithm.

Remark 4: The initial parameters ${\gamma }_{ik}^{(0)}$ are chosen independently and uniformly on (0,1), and each ${\gamma }_i^{(0)}$ is multiplied by a normalizing constant so that ${\sum }_{k=1}^K{\gamma }_{ik}^{(0)}=1$ for every i. We start with an M-step to obtain initial π⁽⁰⁾ and θ⁽⁰⁾.

Remark 5: Using standard arguments that apply to minorization-maximization algorithms [20], we can show that our variational EM algorithm preserves the ascent property of the lower bound of the log-likelihood, namely,

$$\text{LB}\left({\mathit{\pi }}^{(\tau )},{\mathit{\theta }}^{(\tau )};{\mathbf{\Gamma }}^{(\tau )}\right)\le \text{LB}\left({\pi }^{(\tau +1)},{\mathit{\theta }}^{(\tau +1)};{\mathbf{\Gamma }}^{(\tau +1)}\right).$$

4. Model selection

In practice, the number of groups is unknown and should be chosen. Handcock et al. [15] propose a Bayesian method of determining the number of groups by using approximate conditional Bayes factors in a latent position cluster model. Daudin et al. [11] also derive a Bayesian model selection criterion that is based on the integrated classification likelihood (ICL). In this section, we use the conditional likelihood of the network series, given an estimate of the membership vector, to construct an effective model selection criterion.

Algorithm 1.

Variational EM algorithm

• Initialize Γ(0), π(0), and θ(0).

• Iteratively solve the Variational E-step and M-step with τ ∈ {0,1,…} until convergence:

– Variational E-step: Solve Γ(τ+1) from the maximization of $Q\left({\pi }^{(\tau )},{\mathbf{\theta }}^{(\tau )},{\mathbf{\Gamma }}^{(\tau )};\mathbf{\Gamma }\right)$ under the constraints that γi1,…,γiK ≥ 0 and ${\sum }_{k=1}^K{\gamma }_{ik}=1$ for i ∈ {1,…, n};

– Variational M-step: Compute ${\pi }_k^{(\tau +1)}=(1/n){\sum }_{i=1}^n{\gamma }_{ik}^{(\tau +1)}$ for k ∈ {1,…,K}, and solve θ(τ+1) using the modified Newton-Raphson method (13) with the gradient and Hessian of (9).

Let ${\widehat{z}}_{ik}=\mathbb{1}\left({\widehat{\gamma }}_{ik}={\max }_{1\le j\le K}{\widehat{\gamma }}_{ij}\right)$ indicate the assignment of each node to a component once the algorithm has converged. We obtain the conditional log-likelihood of the network series y₁,…, y_T, given initial network y₀ and estimated component membership vector $\widehat{\mathit{z}}=\left({\widehat{\mathit{z}}}_1,\dots ,{\widehat{\mathit{z}}}_n\right)$, as

$$\mathrm{cl}(\mathbf{\theta },\widehat{\mathit{z}})=\ln \mathrm{Pr}\left({\mathbf{y}}_1,\dots ,{\mathbf{y}}_T|{\mathbf{y}}_0,\widehat{\mathit{z}}\right),$$

which can be written using conditional dyadic independence in the form

$$\mathrm{cl}(\mathbf{\theta },\widehat{\mathit{z}})=\sum _{t=1}^T\sum _{i<j}^n\ln \mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij},\widehat{\mathit{z}}\right).$$

We propose the following conditional likelihood Bayesian information criterion to choose the number of groups for our method:

$$\text{CL}-{\text{BIC}}_K=-2\text{cl}({\widehat{\mathit{\theta }}}_{\text{cl}},\widehat{\mathit{z}})+d_K({\widehat{\mathit{\theta }}}_{\text{cl}},\widehat{\mathit{z}})\ln \{Tn(n-1)/2\},$$

where ${\widehat{\mathit{\theta }}}_{\text{cl}}$ is the conditional likelihood estimate given K groups and $d_K(\mathit{\theta },\widehat{\mathit{z}})=\mathrm{tr}\left(H_K^{-1}{V}_K\right)$ is the model complexity, following Vann and Vidoni [41], based on $H_K=\text{E}\left\{-{\nabla }_{\mathbf{\theta }}^2\text{cl}(\mathit{\theta },\widehat{\mathit{z}})\right\}$ and $V_K=\mathrm{var}\left\{{\nabla }_{\mathit{\theta }}\mathrm{cl}(\mathit{\theta },\widehat{\mathit{z}})\right\}$. We choose the optimal K by minimizing the CL-BIC score. The composite likelihood BIC has been previously studied by Saldana et al. [37] for stochastic blockmodels and by Xue et al. [48] for discrete graphical models.

We may derive the explicit conditional likelihood BIC for Examples 1 and 2. For TERGM with stability parameters ${\theta }_1^s,\dots ,{\theta }_K^s$ in Example 1, we obtain

$$\mathrm{cl}\left({\mathit{\theta }}^s,\widehat{\mathit{z}}\right)=\sum _{t=1}^T\sum _{i<j}^n\left[-\ln \left\{1+\exp \left({\theta }_{{\widehat{z}}_i}^s+{\theta }_{{\widehat{z}}_j}^s\right)\right\}+\left\{y_{t,ij}{y}_{t-1,ij}+\left(1-y_{t,ij}\right)\left(1-y_{t-1,ij}\right)\right\}({\theta }_{{\widehat{z}}_i}^s+{\theta }_{{\widehat{z}}_j}^s)\right].$$

For any given K and the corresponding estimate ${\widehat{\mathit{\theta }}}_{\text{cl}}^s$, we derive the explicit estimate of V_K as

$${\widehat{V}}_K({\widehat{\mathit{\theta }}}_{\text{cl}}^s)=\sum _{t=1}^T\mathit{u}({\widehat{\mathit{\theta }}}_{\text{cl}}^s)\mathit{u}{({\widehat{\mathit{\theta }}}_{\text{cl}}^s)}^{\top },$$

where $\mathit{u}({\widehat{\mathit{\theta }}}_{\text{cl}}^s)={\left(u({\widehat{\theta }}_{\text{cl},1}^s),\dots ,u({\widehat{\theta }}_{\text{cl},K}^s)\right)}^{\top }$ and for k ∈ {1,…, K},

$$u({\widehat{\theta }}_{\text{cl},k}^s)=\sum _{i<j}^n\{-\frac{\exp ({\widehat{\theta }}_{\text{cl},{\widehat{z}}_i}^s+{\widehat{\theta }}_{\text{cl},{\widehat{z}}_j}^s)}{1+\exp ({\widehat{\theta }}_{\text{cl},{\widehat{z}}_i}^s+{\widehat{\theta }}_{\text{cl},{\widehat{z}}_j}^s)}{y}_{t,ij}{y}_{t-1,ij}+\left(1-y_{t,ij}\right)\left(1-y_{t-1,ij}\right)\}\left({\widehat{z}}_{ik}+{\widehat{z}}_{jk}\right).$$

We also derive the explicit estimate of H_K denoted by ${\widehat{H}}_K({\widehat{\mathit{\theta }}}_{\text{cl}}^s)$ as follows:

$$\left[\begin{array}{ccc}T{\sum }_{i<j}^n\left[\frac{4\exp ({\widehat{\theta }}_{\text{cl},1}^s+{\widehat{\theta }}_{\text{cl},1}^s)}{{\{1+\exp ({\widehat{\theta }}_{\text{cl},1}^s+{\widehat{\theta }}_{\text{cl},1}^s)\}}^2}\right]I_{i,j}^1& \dots & T{\sum }_{i<j}^n\left[\frac{\exp ({\widehat{\theta }}_{\text{cl},1}^s+{\widehat{\theta }}_{\text{cl},K}^s)}{{\{1+\exp ({\widehat{\theta }}_{\text{cl},1}^{\text{s}}+{\widehat{\theta }}_{\text{cl},K}^{\text{c}})\}}^2}\right]I_{i,j}^{1,K}\\ ⋮& \ddots & ⋮\\ T{\sum }_{i<j}^n\left[\frac{\exp ({\widehat{\theta }}_{\text{cl},K}^s+{\widehat{\theta }}_{\text{cl},1}^s)}{{\{1+\exp ({\widehat{\theta }}_{\text{cl},K}^s+{\widehat{\theta }}_{\text{cl},1}^s)\}}^2}\right]I_{i,j}^{K,1}& \dots & T{\sum }_{i<j}^n\left[\frac{4\exp ({\widehat{\theta }}_{\text{cl},K}^{\text{s}}+{\widehat{\theta }}_{\text{cl},K}^{\text{s}})}{{\{1+\exp ({\widehat{\theta }}_{\text{cl},K}^s+{\widehat{\theta }}_{\text{cl},K}^s)\}}^2}\right]I_{i,j}^K\end{array}\right],$$

where $I_{i,j}^k={\widehat{z}}_{ik}{\widehat{z}}_{jk}$ and $I_{i,j}^{k,l}={\widehat{z}}_{ik}{\widehat{z}}_{jl}+{\widehat{z}}_{il}{\widehat{z}}_{jk}$ for k, l ∈ {1, …, K}. We now obtain the estimate of d_K as ${\widehat{d}}_K=\mathrm{tr}({\widehat{H}}_K^{-1}{\widehat{V}}_K)$. Finally, for Clustering time-evolving networks through TERGM with a stability parameter, we determine the optimal number of groups from

$$\widehat{K}=\arg \underset{K}{\min }\widehat{\text{CL}-\text{BI}}{\text{C}}_K=\arg \underset{K}{\min }-2\text{cl}({\widehat{\mathit{\theta }}}_{\text{cl}}^s,\widehat{\mathit{z}})+{\widehat{d}}_K({\widehat{\mathit{\theta }}}_{\text{cl}}^s,\widehat{\mathit{z}})\ln \{Tn(n-1)/2\},$$

where ${\widehat{\mathit{\theta }}}_{\text{cl}}^s$ and $\widehat{\mathit{z}}$ are the estimates of θ^s and z Corresponding to a given K. The details for STERGM with formation and persistence parameters in Example 2 are presented in the appendix.

We also introduce an alternative model selection Criterion based on modified integrated Classification likelihood. Again for the TERGM with stability parameters, the modified ICL Can be written as

$${\text{ICL}}_K=\sum _{t=1}^T\sum _{i<j}^n\ln \mathrm{Pr}\left(Y_{t,ij}=y_{t,ij}|y_{t-1,ij},\widehat{\mathit{z}}\right)-K\ln \{Tn(n-1)/2\},$$

where the second term penalizes the K stability parameters and we Choose the optimal number of groups as

$$\widehat{K}=\underset{K}{\arg \max }{\text{ICL}}_K.$$

Model selection results using both Conditional likelihood BIC and modified ICL in the simulation studies are presented on Section 5.

5. Simulation studies

5.1. Simulation studies for mixture of TERGMs and STERGMs

Firstly simulation studies were Conducted when the dataset was generated from a mixture of TERGMs and STERGMs. To simulate time-evolving network from the K-Component mixture of TERGMs with stability parameters, i.e., Example 1, we first specify network structure by choosing randomly the categories of the nodes according to the fixed mixing proportions and by defining initial densities for each group. We then obtain the initial network y₀ by simulating all the edges based on the probabilities specified by the density parameters and the categories of the nodes. Next, we set different stability parameters for each group and simulate the edges in networks y₁,…, y_T sequentially, based on the probabilities determined by the parameters, the preceding networks, and the categories of the nodes. Similarly, we simulate time-evolving networks from the K-component mixture of STERGMs with formation and persistence parameters, i.e., Example 2. For each of the four model settings listed in Table 1, we use 100 nodes and 10 discrete time points.

Table 1.

Models 1–2 are two different simulation settings for for TERGM with stability parameters (Example 1) and Models 3–4 are two different simulation settings for STERGM with formation and persistence parameters (Example 2).

	Model 1		Model 2
	G1	G2	G1	G2	G3
Mixing proportion πk	0.5	0.5	0.33	0.33	0.33
Stability parameter ${\theta }_k^s$	−0.5	0.5	−1	0	1
Initial network density parameter ${\theta }_k^d$	−0.5	0.5	−1	0	1
	Model 3		Model 4
	G1	G2	G1	G2	G3
Mixing proportion πk	0.5	0.5	0.33	0.33	0.33
Formation parameter ${\theta }_k^f$	−1.5	1.5	−1.5	0	1.5
Persistence parameter ${\theta }_k^p$	−1	1	−1	0	1
Initial network density parameter ${\theta }_k^d$	−0.5	0.5	−1	0	1

To check the performance of the algorithm at identifying the correct number of groups, we count the frequencies of min CL-BIC and max ICL over 100 repetitions. To assess the clustering performance, we calculate the average value of the Rand Index (RI) and the average value of Normalized Mutual Information (NMI) over the 100 repetitions. The NMI can be used to compare the performance of clusterings with different numbers of clusters since it is a normalized metric. To assess the estimation performance of the algorithm, we calculate the average root squared error for estimated mixing proportions and network parameters over the 100 repetitions: ${\text{RSE}}_{\mathit{\pi }}={({\sum }_{k=1}^K{({\widehat{\pi }}_k-{\pi }_k)}^2)}^{1/2}$ and ${\mathrm{RSE}}_{\mathit{\theta }}={({\sum }_{k=1}^K{({\widehat{\theta }}_k-{\theta }_k)}^2)}^{1/2}$ We check the performance of our criterion functions in choosing the correct number of groups, with K0 denoting the true number of groups. As in Table 2, both CL-BIC and modified ICL perform well. The average values of Rand Index and Normalized Mutual Information are reported in Table 3.

Table 2.

Comparison of the model selection performance using the frequencies of min CL-BIC and max ICL over 100 repetitions. The details about Models 1–4 can be found in Table 1.

	Model 1 (K0 = 2)				Model 2 (K0 = 3)
	K = 1	K = 2	K = 3	K = 4	K = 1	K = 2	K = 3	K = 4
min CL-BIC	0	99	0	1	0	0	97	3
max ICL	0	100	0	0	0	0	96	4
	Model 3 (K0 = 2)				Model 4 (K0 = 3)
	K = 1	K = 2	K = 3	K = 4	K = 1	K = 2	K = 3	K = 4
min CL-BIC	0	99	1	0	0	3	93	4
max ICL	0	100	0	0	0	0	99	1

Table 3.

Comparison of the clustering performance usng the average Rand Index (RI) and Normalized Mutual Information (NMI) for 100 repetitions for various models and values of K, with sample standard deviations in parentheses. The details about Models 1–4 can be found in Table 1.

	Model 1 (K0 = 2)
	K = 2	K = 3	K = 4
RI	1.000 (0.000)	0.874 (0.033)	0.773 (0.030)
NMI	1.000 (0.000)	0.674 (0.043)	0.521 (0.025)
	Model 2 (K0 = 3)
	K = 2	K = 3	K = 4
RI	0.751 (0.044)	0.996 (0.031)	0.943 (0.025)
NMI	0.482 (0.075)	0.990 (0.064)	0.827 (0.045)
	Model 3 (K0 = 2)
	K = 2	K = 3	k = 4
RI	1.000 (0.000)	0.874 (0.033)	0.774 (0.031)
NMI	1.000 (0.000)	0.675 (0.046)	0.521 (0.026)
	Model 4 (K0 = 3)
K = 2	K = 3	K = 4
RI	0.761 (0.045)	0.998 (0.021)	0.945 (0.018)
NMI	0.511 (0.084)	0.995 (0.049)	0.836 (0.033)

Table 4 summarizes the estimation performance of our algorithm using RSE_π, ${\text{RSE}}_{{\mathit{\theta }}^s}$, ${\text{RSE}}_{{\mathit{\theta }}^f}$, and ${\text{RSE}}_{{\mathit{\theta }}^p}$. The results of Tables 2 – 4 together tell us that our algorithm performs convincingly on this set of test datasets. We also found that our proposed algorithm performs convincingly in an unbalanced setting where the cluster proportions are unequal, and these results are provided in the supplementary material.

Table 4.

Comparison of the estimation performance for mixing proportions and network parameters over 100 repetitions with standard deviations shown in parentheses. The details about Models 1–4 and the root squared error can be found in Table 1 and Section 5.1.

Model 1 (K0 = 2)			Model 2 (K0 = 3)
RSEπ		${\text{RSE}}_{{\mathit{\theta }}^s}$	RSEπ		${\text{RSE}}_{{\mathit{\theta }}^s}$
0.056		0.013	0.073		0.038
(0.043)		(0.008)	(0.043)		(0.098)
Model 3 (K0 = 2)			Model 4 (K0 = 3)
RSEπ	${\text{RSE}}_{{\mathit{\theta }}^f}$	${\text{RSE}}_{{\mathit{\theta }}^p}$	RSEπ	${\text{RSE}}_{{\mathit{\theta }}^f}$	${\text{RSE}}_{{\mathit{\theta }}^p}$
0.057	0.030	0.023	0.072	0.045	0.039
(0.043)	(0.020)	(0.015)	(0.040)	(0.094)	(0.071)

5.2. Simulation studies for robustness of model selection

We conduct additional simulation studies to check which model selection criterion is more robust in choosing the correct number of groups when the time-evolving networks are not simulated from the true model. This time we use the ‘simulate.stergm’ function in the tergm package [27] in R [36] to simulate K time-evolving networks [26] and combine them into a larger time-evolving network in which each of the original time-evolving networks is the subnetwork containing nodes from one of the K groups. First, we specify each network structure by choosing randomly the categories of the nodes according to the fixed mixing proportions and by defining the network densities. Next, we set different mean relational durations, which represent different degrees of stability, and simulate each time-evolving network to have the average network density we defined over the time points. Finally, we combine the K time-evolving networks into a single time-evolving network by adding a fixed number of edges between randomly chosen pairs of individuals in different groups. For each of the two model settings listed in Table 5, we use 100 nodes, 10 discrete time points, and 10 edges added between randomly chosen pairs of nodes in different groups.

Table 5.

Models 5–6 are two different simulation settings when the time-evolving networks are not simulated from the true model.

	Model 5		Model 6
	G1	G2	G1	G2	G3
Mixing proportion	0.4	0.6	0.3	0.4	0.3
Mean relational duration	5	2.5	7.5	5	2.5
Average network density	0.15	0.1	0.1	0.25	0.3

As shown in Table 6, in the new simulation setting where the time-evolving networks are not simulated from the true model, CL-BIC still performs well in choosing the correct number of groups using either TERGM with a stability parameter or STERGM with formation and persistence parameters. However, as shown in Table 7, modified ICL fails to choose the correct number of groups. Tables 6 and 7 show that the performance of our proposed CL-BIC in choosing the correct number of groups seems more robust than modified ICL when the model assumptions are violated.

Table 6.

Frequencies of min CL-BIC over 100 repetitions. The details about Models 5–6 can be found in Table 5.

	Model 5 (K0 = 2)				Model 6 (K0 = 3)
	K = 1	K = 2	K = 3	K = 4	K = 1	K = 2	K = 3	K = 4
TERGM	0	87	12	1	0	1	96	3
STERGM	0	93	2	5	0	8	91	1

Table 7.

Frequencies of max ICL over 100 repetitions. The details about Models 5–6 can be found in Table 5.

	Model 5 (K0 = 2)				Model 6 (K0 = 3)
	K = 1	K=2	K = 3	K=4	K = 1	K = 2	K = 3	K=4
TERGM	0	49	23	28	0	0	65	35
STERGM	0	53	32	15	0	0	59	41

The average RI and NMI results are reported in Tables 8 and 9. In all models, TERGM with a stability parameter and STERGM with formation and persistence parameters achieve a high average RI and NMI for the correct number of mixtures. Moreover, we see a fairly high average RI and NMI with the selected (via minimum CL-BIC) number of groups $\widehat{K}$. The results of Tables 6, 8, and 9 together tell us that our algorithm based on CL-BIC can perform convincingly in choosing the correct number of groups and assigning nodes to groups even when the time-evolving networks are not generated from the true model.

Table 8.

Comparison of the clustering performance using average Rand Index with standard deviations shown in parentheses. The details about Models 5–6 can be found in Table 5.

	Model 5 (K0 = 2)
	K = 2	K = 3	K = 4	$K=\widehat{K}$
TERGM	0.976 (0.032)	0.797 (0.045)	0.716 (0.036)	0.948 (0.080)
STERGM	0.979 (0.025)	0.798 (0.054)	0.727 (0.041)	0.966 (0.056)
	Model 6 (K0 = 3)
	K = 2	K = 3	K = 4	$K=\widehat{K}$
TERGM	0.753 (0.054)	0.976 (0.033)	0.935 (0.023)	0.975 (0.037)
STERGM	0.756 (0.055)	0.972 (0.036)	0.931 (0.024)	0.961 (0.052)

Table 9.

Comparison of the clustering performance using average Normalized Mutual Information with standard deviations shown in parentheses. The details about Models 5–6 can be found in Table 5.

	Model 5 (K0 = 2)
	K = 2	K = 3	K=4	$K=\widehat{K}$
TERGM	0.922 (0.093)	0.535 (0.074)	0.403 (0.073)	0.863 (0.179)
STERGM	0.928 (0.076)	0.532 (0.084)	0.410 (0.071)	0.901 (0.131)
	Model 6 (K0 = 3)
	K = 2	K = 3	K = 4	$K=\widehat{K}$
TERGM	0.508 (0.094)	0.936 (0.064)	0.795 (0.044)	0.933 (0.070)
STERGM	0.500 (0.092)	0.926 (0.069)	0.778 (0.050)	0.901 (0.111)

6. Applications to real-world time-evolving networks

Here, we apply our proposed model-based clustering methods to detect groups in two time-evolving network datasets: International trade networks of 58 countries from 1981 to 2000, and collaboration networks of 151 researchers at a large American research university from 2004 to 2013. In particular, we are interested in analyzing the rate of evolution of these time-evolving networks as in Knecht [24], Snijders et al. [39], and Krivitsky and Handcock [26]. Before proceeding, we introduce metrics to measure the instability of edges in the estimated groups ${\text{G}}_1,\dots ,{\text{G}}_{\widehat{K}}$. For $k,l\in \{1,\dots ,\widehat{K}\}$ and t ∈ {1, …, T}, define

• the “1 → 0” instability of edges between G_k and G_l at the time t:

  $${\mathcal{S}}_{1\to 0}^{kl}(t)=\frac{\sum _{i\in {\text{G}}_k,j\in {\text{G}}_l}{y}_{t-1,ij}\left(1-y_{t,ij}\right)}{\sum _{i\in {\text{G}}_k,j\in {\text{G}}_l}{y}_{t-1,ij}{y}_{t,ij}};$$
• the “0 → 1” instability of edges between G_k and G_l at the time t:

  $${\mathcal{S}}_{0\to 1}^{kl}(t)=\frac{\sum _{i\in G_k,j\in {\text{G}}_l}\left(1-y_{t-1,ij}\right)y_{t,ij}}{\sum _{i\in G_k,j\in {\text{G}}_l}\left(1-y_{t-1,ij}\right)\left(1-y_{t,ij}\right)};$$
• the total instability of edges between G_k and G_l at the time t:

  $${\mathcal{S}}_{\text{tot}}^{kl}(t)=\frac{\sum _{i\in {\text{G}}_k,j\in {\text{G}}_l}\left\{y_{t-1,ij}\left(1-y_{t,ij}\right)+\left(1-y_{t-1,ij}\right)y_{t,ij}\right\}}{\sum _{i\in {\text{G}}_k,j\in {\text{G}}_l}\left\{y_{t-1,ij}{y}_{t,ij}+\left(1-y_{t-1,ij}\right)\left(1-y_{t,ij}\right)\right\}}.$$

The three instability statistics defined above evaluate the within-group instability when k = l and the between-group instability when k ≠ l. Next, we define $\mathcal{A}{\mathcal{S}}_{1\to 0}^{kl}$, $\mathcal{A}{\mathcal{S}}_{0\to 1}^{kl}$ and $\mathcal{A}{\mathcal{S}}_{tot}^{kl}$ as the averages over all t of ${\mathcal{S}}_{1\to 0}^{kl}(t)$, ${\mathcal{S}}_{0\to 1}^{kl}(t)$ and ${\mathcal{S}}_{tot}^{kl}(t)$, respectively. Here, a larger value of $\mathcal{A}{\mathcal{S}}_{1\to 0}^{kl}$ indicates that the network is more likely to dissolve ties, a larger value of $\mathcal{A}{\mathcal{S}}_{0\to 1}^{kl}$ implies that the network is more likely to form ties, and a larger value of $\mathcal{A}{\mathcal{S}}_{tot}^{kl}$ implies that the network is less stable overall.

6.1. International trade networks

We first consider finding groups for the yearly international trade networks of n = 58 countries studied by Ward and Hoff [44]. We follow Westveld and Hoff [45] and Saldana et al. [37] to define networks y₁₉₈₁, …, y₂₀₀₀ as follows: for any t ∈ {1981, …, 2000}, y_{t,i j} = 1 if the bilateral trade between country i and country j in year t exceeds the median bilateral trade in year t, and y_{t,i j} = 0 otherwise. By definition, this setup results in networks in which the edge density is roughly one half. Here, we employ model-based clustering through TERGM with a stability parameter, i.e., Example 1.

First, we use our proposed CL-BIC to determine the number of groups and $\widehat{K}=3$ is chosen. Hence, we shall identify three groups of countries based on different degrees of stability.

We summarize the characteristics of the three estimated groups, including some basic network statistics and parameter estimates, in Table 10. We also calculate the within-group and between-group instability measures. As shown in Table 11, group G₃ has the smallest total instability $\mathcal{A}{\mathcal{S}}_{tot}^{33}$, which implies that those countries in G₃ consistently maintain their trading countries. In addition, the “1 → 0” and “0 → 1” instability measures show that countries in group G₂ change their trading countries more actively than countries in G₁ and G₃. To summarize, groups G₁, G₂, and G₃ correspond to the medium stability, low stability, and high stability groups, respectively.

Table 10.

Summary of network statistics, parameter estimates, and average memberships for each group. Groups G₁, G₂, and G₃ correspond to the medium stability, low stability, and high stability groups, respectively.

	G1	G2	G3
Total # of nodes	24	21	13
Average # of edges per node	17.11	34.28	42.42
Average # of triangles per node	150.17	443.95	613.15
Estimated mixing proportion $\widehat{\pi }$	0.3920	0.3677	0.2403
Estimated stability parameter ${\widehat{\theta }}^s$	1.6323	1.3168	2.0712
Average membership of ${\widehat{\gamma }}_{\cdot 1}$	0.8147	0.1158	0.0579
Average membership of ${\widehat{\gamma }}_{\cdot 2}$	0.1060	0.8262	0.1101
Average membership of ${\widehat{\gamma }}_{\cdot 3}$	0.0794	0.0579	0.8320

Table 11.

Summary of within-group and between-group instability statistics for the proposed model-based clustering group assignments for the international trade network dataset. $\mathcal{A}{\mathcal{S}}_{1\to 0}^{kl}$, $\mathcal{A}{\mathcal{S}}_{0\to 1}^{kl}$, and $\mathcal{A}{\mathcal{S}}_{tot}^{kl}$ measure the average over all t of ${\mathcal{S}}_{1\to 0}^{kl}(t)$, ${\mathcal{S}}_{0\to 1}^{kl}(t)$, and ${\mathcal{S}}_{tot}^{kl}(t)$, respectively, with standard deviations shown in parentheses.

$\mathcal{A}{\mathcal{S}}_{1\to 0}^{11}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{11}$	$\mathcal{A}{\mathcal{S}}_{tot}^{11}$	$\mathcal{A}{\mathcal{S}}_{1\to 0}^{22}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{22}$	$\mathcal{A}{\mathcal{S}}_{tot}^{22}$	$\mathcal{A}{\mathcal{S}}_{1\to 0}^{33}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{33}$	$\mathcal{A}{\mathcal{S}}_{tot}^{33}$
0.088	0.014	0.023	0.048	0.248	0.082	0.002	0.014	0.004
(0.094)	(0.009)	(0.013)	(0.041)	(0.132)	(0.047)	(0.006)	(0.034)	(0.006)
$\mathcal{A}{\mathcal{S}}_{1\to 0}^{12}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{12}$	$\mathcal{A}{\mathcal{S}}_{tot}^{12}$	$\mathcal{A}{\mathcal{S}}_{1\to 0}^{13}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{13}$	$\mathcal{A}{\mathcal{S}}_{tot}^{13}$	$\mathcal{A}{\mathcal{S}}_{1\to 0}^{23}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{23}$	$\mathcal{A}{\mathcal{S}}_{tot}^{23}$
0.098	0.042	0.058	0.041	0.048	0.043	0.011	0.049	0.016
(0.030)	(0.014)	(0.015)	(0.021)	(0.026)	(0.008)	(0.017)	(0.088)	(0.019)

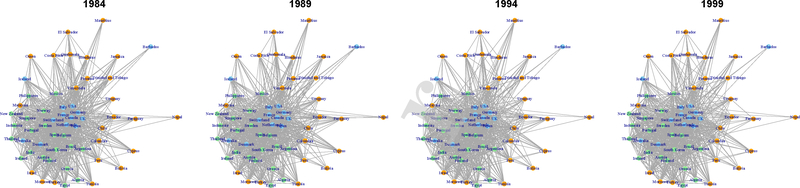
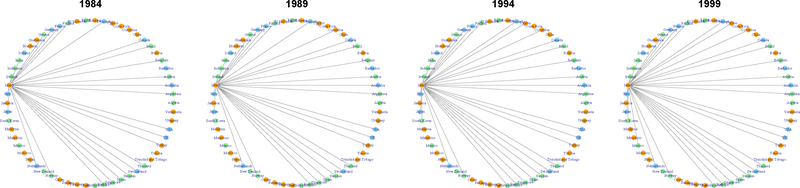
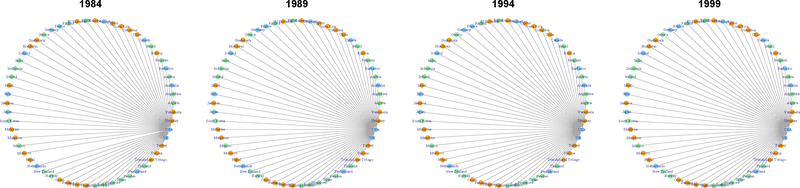
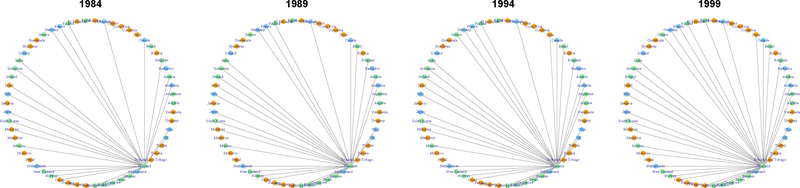
In Fig. 1, we plot the international trade networks with estimated groups represented by orange for G₁, light green for G₂, and light blue for G₃ to illustrate our model-based clustering result. To illustrate how networks change over time for countries in each of the three groups, in Fig. 2 – 4 we isolate one representative country from each group: Israel from G₁, Thailand from G₂, and the United States from G₃.

Fig. 1.

International trade networks with estimated groups in four different years. Nodes assigned to G₁, G₂, and G₃ are colored orange, light green, and light blue, respectively.

Fig. 2.

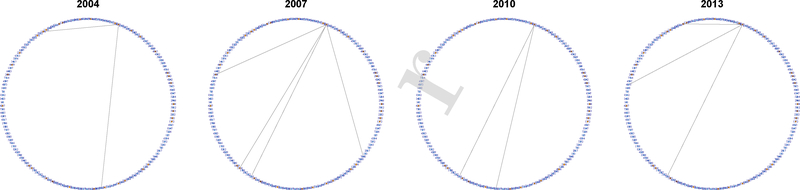
Trade network of Israel, with estimated membership vector $\widehat{\gamma }=(0.711,0.072,0.218)$. Although primarily classified as medium stability, Israel has stable trade with high-level GDP countries in G₃, which explains its 21.8% membership in G₃.

Fig. 4.

Trade network of the United States, with estimated membership vector $\widehat{\mathit{\gamma }}=(0.004,0.000,0.996)$. The United States is solidly in the high-stability group.

6.2. Collaboration networks

We next find groups for the yearly collaboration networks at a large research university from 2004 to 2013. There are n = 151 researchers from various academic units in this dataset. We define networks y₂₀₀₄, …, y₂₀₁₃ as follows: for any t ∈ {2004, …, 2013}, y_{t,i j} = 1 if researcher i and researcher j have an active research grant together during year t, and y_t,ij = 0 otherwise. Here, we employ model-based clustering through STERGM with formation and persistence parameters, i.e., Example 2.

Again, we use our proposed CL-BIC and $\widehat{K}=2$ is chosen as an optimal number of groups. Therefore, we shall identify two groups of researchers based on different degrees of formation and persistence.

Table 12 summarizes their basic network statistics and parameter estimates, while Table 13 displays the within-group and between-group instability measures. As these tables show, G₁ has higher “1 → 0”, “0 → 1”, and total instability than G₂. Thus, the researchers in G₁ tend to have fewer stable collaborations and work with more collaborators than those in G₂.

Table 12.

Summary of network statistics, parameter estimates, and average memberships for each group. Groups G₁ and G₂ correspond to the low stability and high stability groups.

	G1	G2
Total # of nodes	34	117
Average # of edges per node	2.92	1.90
Average # of triangles per node	0.8088	0.3957
Estimated mixing proportions $\widehat{\pi }$	0.2464	0.7536
Estimated formation parameter ${\widehat{\theta }}^f$	−2.2677	−2.9634
Estimated persistence parameter ${\widehat{\theta }}^p$	0.1647	0.6156
Average membership of ${\widehat{\gamma }}_{\cdot 1}$	0.7706	0.0941
Average membership of ${\widehat{\gamma }}_{\cdot 2}$	0.2294	0.9059

Table 13.

Summary of within-group and between-group instability statistics for the proposed model-based clustering group assignments for the collaboration network dataset. $\mathcal{A}{\mathcal{S}}_{1\to 0}^{kl}$, $\mathcal{A}{\mathcal{S}}_{0\to 1}^{kl}$, and $\mathcal{A}{\mathcal{S}}_{tot}^{kl}$ measure the average over all t of ${\mathcal{S}}_{1\to 0}^{kl}(t)$, ${\mathcal{S}}_{0\to 1}^{kl}(t)$, and ${\mathcal{S}}_{tot}^{kl}(t)$, respectively, with standard deviations shown in parentheses.

$\mathcal{A}{\mathcal{S}}_{1\to 0}^{11}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{11}$	$\mathcal{A}{\mathcal{S}}_{tot}^{11}$	$\mathcal{A}{\mathcal{S}}_{1\to 0}^{22}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{22}$	$\mathcal{A}{\mathcal{S}}_{tot}^{22}$	$\mathcal{A}{\mathcal{S}}_{1\to 0}^{12}$	$\mathcal{A}{\mathcal{S}}_{0\to 1}^{12}$	$\mathcal{A}{\mathcal{S}}_{tot}^{12}$
0.672	0.014	0.029	0.2/2	0.003	0.005	0.540	0.005	0.010
(0.359)	(0.006)	(0.007)	(0.059)	(0.001)	(0.001)	(0.189)	(0.001)	(0.002)

Compared to TERGM with a stability parameter, STERGM with formation and persistence parameters provide more detailed insights about time-evolving networks. Based on the parameter estimates in Table 12, in each group, the stability is more explained by the persistence parameter than the formation parameter. In view of this fact, we further calculate the mean relational duration using the persistence parameter estimates for each estimated group. We obtain the mean relational durations of 2.18 years for G₁ and 2.85 years for G₂.

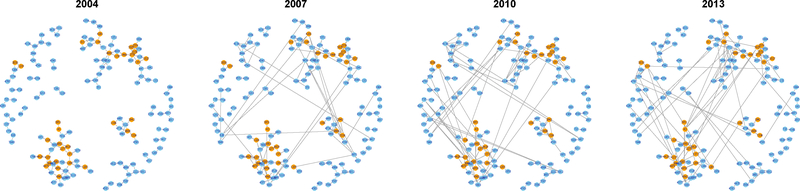
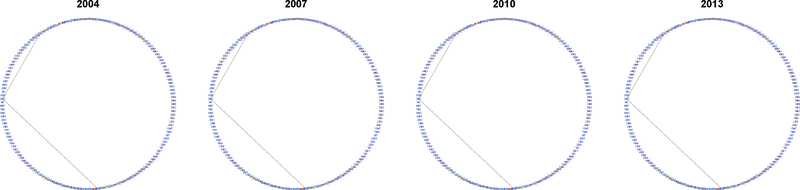
Fig. 5 presents the collaboration networks with estimated groups represented by orange for G₁ and light blue for G₂. We also plot the networks of several representative individual researchers, anonymized by the assignment of four-digit identification numbers, in Fig. 6 – 8.

Fig. 5.

Collaboration networks with estimated groups in four different years. Nodes assigned to G₁ and G₂ are colored orange and light blue, respectively.

Fig. 6.

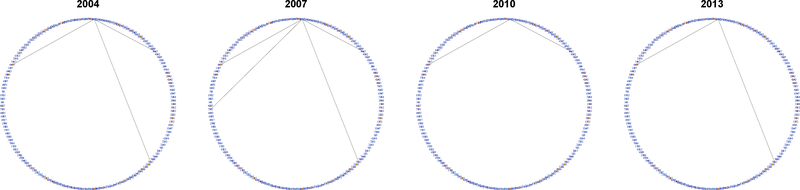
Collaboration network of researcher #4201, with estimated membership vector $\widehat{\mathit{\gamma }}=(0.8506,0.1494)$.

Fig. 8.

Collaboration network of researcher #4607, with estimated membership vector $\widehat{\mathit{\gamma }}=(0.4000,0.6000)$.

7. Conclusions

We propose a novel model-based clustering framework for time-evolving networks based on discrete time exponential-family random graph models, which simultaneously allows modeling and detecting group structure. Our model-based framework achieves different goals than a dynamic stochastic blockmodel framework. For example, the communities found via the latter framework are by assumption sets of nodes with higher edge probability within the sets than between the sets. By contrast, our model-based clustering framework allows for groups to be differentiated by other time-evolving features of interest.

Our model can be extended as follows. First, the network parameters can be modeled as time-varying functions (e.g., [30]) instead of constants. For example, Corneli et al. [10] propose a model for dynamic networks based on conditional non-homogeneous Poisson point processes where intensity functions are dependent on the node memberships and assumed to be stepwise constant, with common discontinuity points. Secondly, to effectively capture the time-evolving group structure of discrete tune exponential-family random graph models, we can incorporate a hidden Markov structure into our model.

Fig. 3.

Trade network of Thailand, with estimated membership vector $\widehat{\mathit{\gamma }}=(0.049,0.910,0.041)$. Primarily classified in the low-stability group, Thailand’s economic boom from 1987 to 1996 was triggered by its improved foreign trade and influx of foreign investment, which is consistent with its rapidly increasing number of trading partners.

Fig. 7.

Collaboration network of researcher #3423, with estimated membership vector $\widehat{\mathit{\gamma }}=(0.0175,0.9825)$.

Appendix

We first present the complete proof of Theorem 1 and then include the details for the proposed conditional likelihood BIC for STERGM with formation and persistence parameters.

Proof of Theorem 1

The proof consists of three parts. First, we show that the mixing proportions π_k, k ∈ {1 …, K}, and the conditional probability of observing an edge p_kl = Pr(Y_t,ij = 1 | y_t−1,ij, Z_ik = Z_jl = 1), k, l ∈ {1, …, K}, k ≤ l, are generically identifiable. Next, we recover the network parameters by showing there exist unique closed-form expressions of θ_k, k ∈ {1, …, K} in terms of the conditional probability of observing an edge. We assume that there are no linear dependencies among the network statistics. Finally, we derive the condition on the number of different network parameters considered in the model to maintain the identifiability.

Allman et al. [4] show in Theorem 2 that it is possible to generically identify the mixing proportions and the conditional probability of observing an edge in the random graph mixture model with binary edge state variables. In our proposed model, the conditional probability of observing an edge is separated into two cases when y_{t−1,i j} = 0 and y_{t−1,i j} = 1, and we are able to obtain similar matrix A as in the proof of Thorem 2 in Allman et al. [4] containing the probabilities of observing the network time series, conditional on the node states. Then as in Allman et al. [3], Lemma 16, we partition the nodes to obtain three sequences of pairwise edge-disjoint subnetworks with corresponding matrix of probabilities and apply Kruskal’s Theorem [29, Theorem 4a]. Finally, with an appropriate marginalization as in the proof of Thorem 2 in Allman et al. [4], we are able to recover the the mixing proportions and the conditional probability of observing an edge.

Now to recover the network parameters, we show there exist unique closed-form expressions of θ_k, k ∈ {1, …, K} in terms of p_kl, k, l ∈ {1, …, K}, k ≤ l and these expressions can be obtained by exploiting the convex duality of exponential families. Let

$${\psi }^{*}\left(\mathit{\mu },y_{t-1,ij}\right)=\underset{\mathit{\theta }}{\sup }\left\{{\mathit{\theta }}^{\top }\mathit{\mu }-\psi \left(\mathit{\theta },y_{t-1,ij}\right)\right\}$$

be the Legendre-Fenchel transform of ψ(θ, y_{t−1,i j}), where the subscripts k and l have been dropped and μ = μ(θ) = E_θ{g(Y_t,Y_t−1)} is the mean value parameter vector whose entries are the expectations of the corresponding network statistics when θ is the canonical parameter. Here, ψ(θ, y_{t−1,i j}) can be written as

$$\psi \left(\mathit{\theta },y_{t-1,ij}\right)=\underset{\mathit{\mu }}{\sup }\left\{{\mathit{\theta }}^{\top }\mathit{\mu }-{\psi }^{*}\left(\mathit{\mu },y_{t-1,ij}\right)\right\}=\underset{\mathit{p}}{\sup }\left[{\mathit{\theta }}^{\top }\mathit{\mu }(\mathit{p})-{\psi }^{*}\left\{\mathit{\mu }(\mathit{p}),y_{t-1,ij}\right\}\right],$$

where $\mathit{\mu }(\mathit{p})={\sum }_{y^{*}\in \{0,1\}}\mathit{g}\left(y^{*},y_{t-1,ij}\right)\mathrm{Pr}\left(Y_{t,ij}=y^{*}|y_{t-1,ij},z\right)$ and ${\psi }^{*}\left\{\mathit{\mu }(\mathit{p}),y_{t-1,ij}\right\}={\sum }_{y^{*}\in \{0,1\}}\mathrm{Pr}\left(Y_{t,ij}=y^{*}|y_{t-1,ij},z\right)\ln \mathrm{Pr}\left(Y_{t,ij}=y^{*}|y_{t-1,ij},\mathit{z}\right)$ since the Legendre-Fenchel transform of ψ(θ, y_{t−1,i j}) is self-inverse [43].

Hence, closed-form expressions of θ in terms of p can be found by maximizing θ^⊤ μ(p) – ψ*{μ(p), y_{t−1,i j}} with respect to p and it is unique since the natural parameter space is convex for an exponential family and θ^⊤ μ(p) – ψ*{μ(p), y_{t−1,i j}} is strictly concave in p.

To show θ^⊤ μ(p) – ψ*{μ(p), y_{t−1,i j}} is strictly concave, we show the Hessian is negative definite. Let c be the cardinality of |p|, then the Hessian H_c is a c × c diagonal matrix with diagonal elements ${\left(-1/p_{y^{*}}\right)}_{y^{*}\in \{0,1\}}$. Here, −H_c is positive definite because the determinants of all upper-left sub-matrices are positive and therefore, H_c is negative definite.

Lastly, we further need conditions on the choice and number of different network parameters considered in the model. First, the network parameters should be chosen carefully in the model such that we avoid linear dependencies among the corresponding network statistics. Secondly, let p be the number of different network parameters considered in the model. For fixed K, we have K p total network parameters and this value cannot be greater than K+{K(K−1)}/2, which is the number of identifiable conditional probabilities of observing an edge between two nodes given edge state of previous time point and their membership labels. Hence, the maximum number of different network parameters identifiable in the model is ⌊(K + 1)/2⌋ where ⌊·⌋is a floor function.

Conditional likelihood BIC for STERGM with formation and persistence parameters

Let ${\widehat{k}}_i$ denote the component assigned to node i by the ${\widehat{\mathit{z}}}_i$ vector, i.e., the value of k such that ${\widehat{z}}_{ik}=1$ The conditional log-likelihood of STERGM with formation and persistence parameters can be written as

$$\mathrm{cl}\left({\mathit{\theta }}^f,{\mathit{\theta }}^p,\widehat{z}\right)=\sum _{t=1}^T\sum _{i<j}^n\left\{-\ln \mathcal{C}\left({\mathit{\theta }}^f,{\mathit{\theta }}^p\right)+\left(y_{t,ij}-y_{t,ij}{y}_{t-1,ij}\right)({\theta }_{{\widehat{k}}_i}^f+{\theta }_{{\widehat{k}}_j}^f)+\left(y_{t,ij}{y}_{t-1,ij}\right)({\theta }_{{\widehat{k}}_i}^p+{\theta }_{{\widehat{k}}_j}^p)\right\},$$

where $\mathcal{C}\left({\mathit{\theta }}^f,{\mathit{\theta }}^p\right)=\{1+\exp {({\theta }_{{\widehat{k}}_i}^p+{\theta }_{{\widehat{k}}_j}^p)\}}^{y_{t-1,ij}}{\{1+\exp ({\theta }_{{\widehat{k}}_i}^f+{\theta }_{{\widehat{k}}_j}^f)\}}^{1-y_{t-1,ij}}.$

For any given K and the corresponding estimates ${\widehat{\mathit{\theta }}}_{\text{cl}}^f$ and ${\widehat{\mathit{\theta }}}_{\text{cl}}^p$ we derive the explicit estimate of V_K as

$${\widehat{V}}_K({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p)=\sum _{t=1}^{T}u({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p)u{({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p)}^{\top },$$

where $u({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p)={\left(u({\widehat{\theta }}_{\text{cl},1}^f),\dots ,u({\widehat{\theta }}_{\text{cl},K}^f),u({\widehat{\theta }}_{\text{cl},K+1}^p),\dots ,u({\widehat{\theta }}_{\text{cl},2K}^p)\right)}^{\top }$ and for k ∈ {1,…,K},

$$u({\widehat{\theta }}_{\text{cl},k}^f)=\sum _{i<j}^n\left\{-\frac{\left(1-y_{t-1,ij}\right)\exp \left({\widehat{\theta }}_{\text{cl},\widehat{z}i}^f+{\widehat{\theta }}_{\text{cl},{\widehat{z}}_j}^f\right)}{1+\exp \left({\widehat{\theta }}_{\text{cl},{\widehat{z}}_i}^f+{\widehat{\theta }}_{\text{cl},{\widehat{z}}_j}^f\right)}+y_{t,ij}-y_{t,ij}{y}_{t-1,ij}\right\}\left({\widehat{z}}_{ik}+{\widehat{z}}_{jk}\right),$$

and for l ∈ {K + 1,..., 2K},

$$u({\widehat{\theta }}_{\text{cl},l}^p)=\sum _{i<j}^n\left\{-\frac{y_{t-1,ij}\exp \left({\widehat{\theta }}_{\text{cl},{\widehat{z}}_i}^p+{\widehat{\theta }}_{\text{cl},{\widehat{z}}_j}^p\right)}{1+\exp \left({\widehat{\theta }}_{\text{cl},{\widehat{z}}_i}^p+{\widehat{\theta }}_{\text{cl},{\widehat{z}}_j{}_j}^p\right)}+y_{t,ij}{y}_{t-1,ij}\right\}\left({\widehat{z}}_{il}+{\widehat{z}}_{jl}\right).$$

We also derive the explicit estimate of H_K as

$${\widehat{H}}_K({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p)=\left[\begin{array}{cccccc}{\widehat{H}}_{11}& \dots & {\widehat{H}}_{1K}& 0& \dots & 0\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ {\widehat{H}}_{K1}& \dots & {\widehat{H}}_{KK}& 0& \dots & 0\\ 0& \dots & 0& {\widehat{H}}_{(K+1)(K+1)}& \dots & {\widehat{H}}_{(K+1)(2K)}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ 0& \dots & 0& {\widehat{H}}_{(2K)(K+1)}& \dots & {\widehat{H}}_{(2K)(2K)}\end{array}\right],$$

where

$$\begin{gathered} {\widehat{H}}_{11}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{4(1-y_{t-1,ij})\exp ({\widehat{\theta }}_{\text{cl},1}^f+{\widehat{\theta }}_{\text{cl},1}^f)}{{\left\{1+\exp ({\widehat{\theta }}_{\text{cl},1}^f+{\widehat{\theta }}_{\text{cl},1}^f)\right\}}^2}\right]I_{i,j}^1,{\widehat{H}}_{1K}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{(1-y_{t-1,ij})\exp ({\widehat{\theta }}_{\text{cl},1}^f+{\widehat{\theta }}_{\text{cl},K}^f)}{{\left\{1+\exp ({\widehat{\theta }}_{\text{cl},1}^f+{\widehat{\theta }}_{\text{cl},K}^f)\right\}}^2}\right]I_{i,j}^{1,K}, \\ {\widehat{H}}_{K1}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{(1-y_{t-1,ij})\exp ({\widehat{\theta }}_{\text{cl},K}^f+{\widehat{\theta }}_{\text{cl},1}^f)}{{\left\{1+\exp ({\widehat{\theta }}_{\text{cl},K}^f+{\widehat{\theta }}_{\text{cl},1}^f)\right\}}^2}\right]I_{i,j}^{K,1},{\widehat{H}}_{KK}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{4(1-y_{t-1,ij})\exp ({\widehat{\theta }}_{\text{cl},K}^f+{\widehat{\theta }}_{\text{cl},K}^f)}{{\{1+\exp ({\widehat{\theta }}_{\text{cl},K}^f+{\widehat{\theta }}_{\text{cl},K}^f)\}}^2}\right]I_{i,j}^K, \\ {\widehat{H}}_{(K+1)(K+1)}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{4y_{t-1,ij}\exp ({\widehat{\theta }}_{\text{cl},1}^p+{\widehat{\theta }}_{\text{cl},1}^p)}{{\left\{1+\exp ({\widehat{\theta }}_{\text{cl},1}^p+{\widehat{\theta }}_{\text{cl},1}^p)\right\}}^2}\right]I_{i,j}^1,{\widehat{H}}_{(K+1)(2K)}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{y_{t-1,ij}\exp ({\widehat{\theta }}_{\text{cl},1}^p+{\widehat{\theta }}_{\text{cl},K}^p)}{{\left\{1+\exp ({\widehat{\theta }}_{\text{cl},1}^p+{\widehat{\theta }}_{\text{cl},K}^p)\right\}}^2}\right]I_{i,j}^{1,K}, \\ {\widehat{H}}_{(2K)(K+1)}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{y_{t-1,ij}\exp ({\widehat{\theta }}_{\text{cl},K}^p+{\widehat{\theta }}_{\text{cl},1}^p)}{\{1+\exp {({\widehat{\theta }}_{\text{cl},K}^p+{\widehat{\theta }}_{\text{cl},1}^p)\}}^2}\right]I_{i,j}^{K,1},{\widehat{H}}_{(2K)(2K)}=\sum _{t=1}^T\sum _{i<j}^n\left[\frac{4y_{t-1,ij}\exp ({\widehat{\theta }}_{\mathrm{cl},K}^p+{\widehat{\theta }}_{\text{cl},K}^p)}{{\left\{1+\exp ({\widehat{\theta }}_{\text{cl},K}^p+{\widehat{\theta }}_{\text{cl},K}^p)\right\}}^2}\right]I_{i,j}^K. \end{gathered}$$

In the equations above, $I_{i,j}^k={\widehat{z}}_{ik}{\widehat{z}}_{jk}$ and $I_{i,j}^{k,l}={\widehat{z}}_{ik}{\widehat{z}}_{jl}+{\widehat{z}}_{il}{\widehat{z}}_{jk}$ for k, l ∈{1,…K}.

We now obtain the estimate of d_K as ${\widehat{d}}_K=\mathrm{tr}({\widehat{H}}_K^{-1}{\widehat{V}}_K)$. Finally, for clustering time-evolving networks through STERGM with formation and persistence parameter, ^re determine the optimal number of groups from

$$\widehat{K}=\arg \underset{K}{\min }\widehat{\text{CL}-\text{BI}}{\text{C}}_K=\arg \underset{K}{\min }-2\mathrm{cl}({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p,\widehat{z})+{\widehat{d}}_K({\widehat{\mathit{\theta }}}_{\text{cl}}^f,{\widehat{\mathit{\theta }}}_{\text{cl}}^p,\widehat{z})\ln \{Tn(n-1)/2\},$$

where ${\widehat{\mathit{\theta }}}_{\text{cl}}^f$, ${\widehat{\mathit{\theta }}}_{\text{cl}}^p$ and $\widehat{\mathit{z}}$ are the estimates of θ^f, θ^p and z for a given K.