Fig. 3. Material parameters of fibrin rupture and fitting to the model.
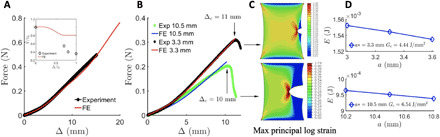
(A) Force-displacement curve for a uniaxial test used to fit the parameters in the FE model. The unfolded proteins aggregate via hydrophobic interactions, expelling the water leading to a volume decrease. The FE model underestimates the amount of liquid lost (the reason is discussed in section S5). (B) Match between the force-displacement curves from the experiments and the finite element model predictions using the parameters fitted from (A) for crack lengths a* = 3.3 and 10.5 mm. The crack tip starts propagating when the overall displacement Δ = Δc. Δc decreases with the crack length a* (see Fig. 2B). Exp corresponds to the experimental results while FE corresponds to the finite element analysis. (C) Surface plots for maximum principal logarithmic strain when Δ = Δc. Strain concentration is observed near the crack. (D) Computation of energy release rate Gc. For crack lengths a* = 3.3 and 10.5 mm, Gc = 4.44 and 6.54 J/m*, respectively. The FE model is used to compute the potential energies for specimens with crack lengths a* ± δ stretched to Δ = Δc : W[Δc(a*), a* ± δ ] and Gc = − (1/t)∂W[Δc(a*), a]/∂a∣Δ = Δc, a = a*.
