Uncertainty analysis for ac-dc difference measurements with the AC Josephson Voltage Standard

Abstract

A detailed analysis of the uncertainties obtained in ac-dc difference measurements with an AC Josephson Voltage Standard (ACJVS) is presented. For audio frequencies and for voltages less than 200 mV, ac-dc transfers with the ACJVS may reduce the combined uncertainty by factors of 2 to 10, compared with conventional methods based on thermal converters. Type A uncertainties are predominantly limited by the thermal transfer standard (TTS), or the digital voltmeter used to acquire the output voltage from the TTS. In agreement with earlier work, the transmission line is the primary contributor to Type B errors for frequencies above 10 kHz. A Monte Carlo sensitivity analysis is used to demonstrate how the uncertainties of transmission line impedance and on-chip inductance impact the accuracy of the rms amplitude conveyed to the TTS.

1. Introduction

The forthcoming redefinition of the SI is motivated in part by the success of quantum-based electrical standards, such as those based on the Josephson effect [1]. The appeal of standards with realizable physical quantities, which are traceable to fundamental constants, invariant with respect to time and environment, and readily disseminated cannot be overstated. Over a period of roughly two decades, the conventional Josephson voltage standard (CJVS) reduced dc voltage measurement uncertainty by about four orders of magnitude over the Weston cell standards of the early 20th century.

With the advent of the pulse-driven Josephson voltage standard in 1996, similar improvements in ac voltage uncertainty were expected [2]. After decades of development (see e.g., [3] and references therein), the pulse-driven JVS, herein referred to as the AC Josephson Voltage Standard (ACJVS)^‡, has indeed improved uncertainties for some regions of voltage-frequency space. However, the frequency response of the interconnection between the ostensibly perfect voltage on-chip and the device under test (DUT) presents significant challenges to scaling beyond audio frequencies. The fundamental issue is that the transmission line cannot be sufficiently characterized to provide a suitably-accurate correction without resorting to calibration with artifact standards [4].

The National Institute of Standards and Technology (NIST) has been actively disseminating Josephson Voltage Standards under its Standard Reference Instrument program [5] to U.S. primary standards laboratories, as well as to National Metrology Institutes in other countries. This program now includes the ACJVS, and thus a comprehensive uncertainty analysis is warranted in order to help end users understand the limitations of such instrumentation. Presently, the most common application for the ACJVS is ac-dc difference calibration of commercial thermal transfer standards (TTS). As a result, such measurements are the primary focus in this report.

2. Operating Principle of the ACJVS

The operating principle of all Josephson voltage standards is the inverse Josephson effect, in which the Josephson junction functions as an ideal frequency-to-voltage converter. For a dc output voltage, this relationship is expressed as,

$$V_{\text{dc}}=\frac{nNhf}{2e},$$ (1)

where n is an integer representing the Shapiro step, or spike, to which the junctions are biased, N is the number of junctions, h is the Planck constant, e is the charge of an electron, and f is the frequency of the applied microwave bias.

For the ACJVS, it is the pulse area quantization behavior of the Josephson junctions that yields a practical ac voltage standard. This follows from the Josephson relationship between the instantaneous voltage v(t) and the phase difference ϕ(t) across the junction,

$$v(t)=\frac{\hslash }{2e}\frac{d\varphi }{dt}.$$ (2)

If the junction is biased with a dc current below its critical current threshold I_c, ϕ is constant and the junction produces zero voltage. If the dc bias I > I_c, ϕ(t) will evolve monotonically in time.

Now, if a current pulse is applied to the junction in such a way that the net change in ϕ is 2π we have,

$$\int v(t)dt=\frac{\hslash }{2e}\int \frac{d\varphi }{dt}dt=\frac{h}{2e},$$ (3)

and thus the junction produces an output pulse with a voltage-time area of one flux quantum, Φ₀ = h/2e. In order to synthesize a sinusoid, for example, a sequence of flux quanta are generated in which the interval between pulses varies inversely with the voltage of the sine wave. Such pulse-density encoding of the waveform is performed by a delta-sigma modulator (described below).

As the pulse duration and spacing is of order 10 ps, the instantaneous output voltage is extremely broadband, containing spectral content from below the audio band to several tens of gigahertz. For rms measurements, this raw waveform must be appropriately lowpass filtered, so that the power in the higher frequency bands is insignificant relative to the power in the tone itself.

2.1. Delta-Sigma modulation

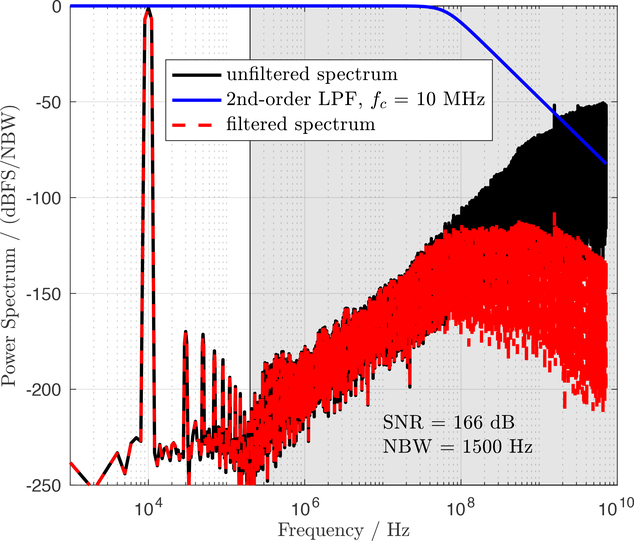
In order to synthesize a pulse pattern appropriate for a specific waveform, an oversampled delta-sigma modulator is employed that converts the mathematically-defined waveform into a corresponding pulse pattern. This initial conversion occurs entirely in the digital realm, but is an analog-to-digital transformation in the sense that the initial waveform samples are represented in double precision and the pulse pattern samples are represented by only 2 to 3 discrete levels (e.g., −1, 0, +1 for a bipolar waveform). Once the pulse pattern is created, it is then uploaded to a pattern generator, which delivers the microwave pulse sequence to the ACJVS. The Josephson junction array(s), in turn, transform the incoming “digital” pulse pattern into an analog waveform whose voltage is traceable to fundamental constants. A representative plot of the spectral density of the pulse pattern is shown in Fig. 1. The encoded waveform is a 10 kHz sinusoid with an amplitude that is −1 dB with respect to the full scale amplitude of a given Josephson junction array^§. The in-band part of the spectrum is shown with white background, while the typical out-of-band span is depicted with a gray background. The in-band signal-to-noise ratio (SNR) is 166 dB. As a point of reference, a commercial 24-bit delta-sigma audio digital-to-analog converter (DAC) of comparable bandwidth has a typical SNR of 80 dB to 100 dB. Likewise, the spurious free dynamic range (SFDR) of the ACJVS pulse pattern for a 1 kHz sine wave is 210 dB (not shown), whereas a commercial audio DAC might have an SFDR as low as 120 dB.

Figure 1:

Calculated power spectrum of the delta-sigma pulse sequence for a 10 kHz sine wave. The raw spectrum is shown in black, the response of a 2nd-order low-pass filter is shown by the blue curve, and the filtered spectrum is depicted by the red dashed line. The white area indicates the region over which the signal-to-noise ratio is calculated. The input pulse sequence was processed with a Hann window prior to computing the spectrum. The power spectrum is sinewave-scaled and the ordinate units are decibels with respect to modulator full-scale per noise bandwidth (cf. Ref. [6] for details.)

2.2. Typical performance operating space

As with the other JVSs, many thousands of junctions are needed to generate voltages relevant for ac metrology. Pushing the upper amplitude beyond 1 V is an active research effort [7], and faces integration challenges both on-chip and in terms of bias electronics. For example, a 1 V ACJVS requires at least two separate microwave biases and four separate low-frequency compensation biases. An rms voltage of 2 V has been achieved without increasing the number of microwave lines, through the use of additional on-chip Wilkinson dividers [8]. But, such a device would require 8 compensation lines, or the number of junctions per array would need to be doubled.

At present, the ACJVS frequency range spans the space between 1 Hz to more than 10 MHz, as well as dc. Note that while the ACJVS is capable of operating in this space, the respective uncertainties may vary greatly. The output bandwidth is predominantly limited by the pattern generator memory for low frequencies, and by the transmission line interconnect at high frequencies. The maximum possible voltage in a waveform scales with the update, or symbol, rate f_s of the pattern generator. The symbol rate is usually fixed at an upper limit, contingent upon the capabilities of the pattern generator or the characteristic frequency of the Josephson junctions. The symbol rate for ACJVS systems at the United States National Institute of Standards and Technology (NIST) is typically (10 to 20) GHz.

Commercial instrumentation is available that can generate pulse patterns at update rates near 100 GHz and store pulse sequences larger than 4 GSa (1 GSa = one billion samples), although both of these capabilities may not exist in the same instrument. For a given symbol rate and pulse pattern length L, we can determine the pattern repetition rate f₀ = f_s/L. The large pattern memory allows waveforms with periods of up to 1 s. Naturally, such patterns require correspondingly long wait times to upload the sequence to the generator and to verify proper quantum operation.

By way of comparison, the Programmable Josephson Voltage Standard (PJVS) can be configured to provide time-dependent waveforms with very high accuracy for frequencies below 100 Hz with no appreciable time penalty [9]. However, such piecewise-defined waveforms would not be suitable for rms measurements.

3. Experimental Configuration

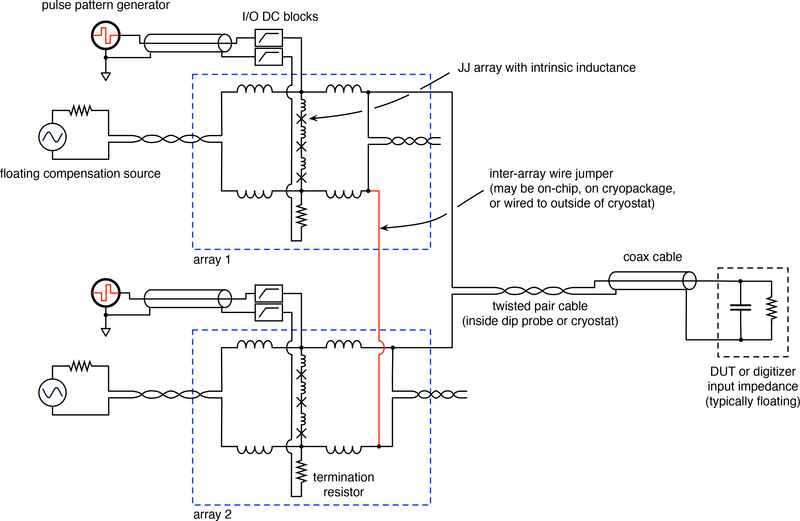
For evaluation of Type A uncertainties and for validation of certain Type B error models, we used a specific experimental configuration (summarized in Table 1) involving an ACJVS die with two Josephson junction arrays and a Fluke 792A thermal transfer standard ^∥. Additional details concerning this experimental arrangement are discussed in 6.2.4 and a simplified schematic is given in Figure 2.

Table 1:

Parameters of the Josephson junction devices and experimental equipment used to determine uncertainties in this report.

Equipment	Make/Model/Parameter	Comments
Device/cryopackage	NIST Superconductive Electronics Group	Dip probe is wired with separate output transmission lines for each array, and for the two arrays in series.
Number of arrays	2	Arrays connected in series on cryopackage with Cu wire for V = 200 mV.
Number of JJs per array	6400
Critical current (nominal)	5 mA
Pulse pattern generator	HSCC ABG-2
Digitizer	NI PXI-5922
Compensation bias amplifier	VMetrix A-200	Isolation from ground is approximately 1 MΩǁ40 pF.
Inner/Outer DC Blocks	Cinch DCB-3511	Cutoff frequency ≈ 500 MHz

Figure 2:

Schematic of the dual-array ACJVS network used in this report, showing the arrangement of bias sources, Josephson junction arrays, and their interconnection. The connection shown here corresponds to that used when both arrays are operated in series to obtain an rms voltage of 200 mV. For rms voltages less than or equal to 100 mV, each array was used separately, and the jumper removed.

The dip probe was configured differently for single-array and dual-array measurements. For measurements at an rms voltage of 200 mV, a copper jumper wire was used at the cryopackage to connect the two arrays and a separate transmission line was run from the cryopackage to a separate output port at the room temperature end of the probe. For all other voltages, the arrays were configured with independent output lines. The experimental parameter space spans frequencies from 100 Hz to 100 kHz, and rms voltages from 2 mV to 200 mV.

4. Limitations and Comparison to Earlier Work

Systematic errors specific to the ACJVS have been discussed extensively in [4, 10, 11, 12, 13, 14]. Uncertainty analyses for the ACJVS that consider most, if not all, known error sources have been presented in [15, 16], as well as in international comparisons using a Fluke 792A as the transfer standard [17, 18]. In Refs. [10, 15], it was highlighted that several systematic errors, such as those due to pulse bias feedthrough and compensation bias, can be largely mitigated through optimized device layout/fabrication and improved experimental bias hardware. The ACJVS system used in this work incorporates many of these advancements, including (1) refined on-chip low-pass filter design [19, 20] and (2) integrated bias electronics that combine both the bitstream generator, CW microwave generator, and compensation generator into a single enclosure with very good control over synchronization [21].

In cases where systematic errors cannot be satisfactorily reduced through engineering, procedures have been developed to measure and correct for errors related to compensation bias [10], dc blocks and feedthrough in the pulse bias [10, 11, 12], and the output transmission line [11, 12, 4, 13, 14]. The utility of these correction procedures depends on the particular error being considered. Unfortunately, in some instances corrections are used without considering the uncertainty involved in their derivation or measurement. For example, using room-temperature measurements of ACJVS transmission line parameters to correct for the line’s response neglects temperature-dependent phenomena like the skin effect, which can be significant above 20 kHz.

The focus in this report is to assist non-expert users of the ACJVS to better understand its most significant limitations and to develop their own uncertainty budgets. For reasons related to inexperience or limited time, we find that calibration staff usually wish to avoid the tedious measurements or simulations required for proper correction of ACJVS systematic errors. On the other hand, calibration staff are keenly interested in a quantitative assessment of the uncorrected uncertainties. As a result, this report does not present the lowest attainable uncertainties for any given ACJVS, nor does it present the worst-case uncertainties of all ACJVS systems. Rather, we outline the mechanisms responsible for the known systematics and provide nominal estimates of their relative contributions to the overall uncertainty budget. For compensation and transmission line systematics, particular attention has been given to estimating the uncertainty involved if a user wishes to perform their own correction.

Two uncertainty summaries are provided below: one assuming a user makes no corrections to systematic errors (“Uncorrected”) and another where it is assumed that a user properly corrects for the transmission line and quadrature effects (“Corrected”). If it is preferable, the reader may interpret the corrected uncertainties as “achievable” uncertainties. The only uncertainties claimed or realized in this report are those of the uncorrected category. Type A uncertainties obtained from measurements with a TTS are only included in the final, overall uncertainties. All other uncertainties are considered of Type B, even if statistical methods were involved in their estimation (as in the Monte Carlo simulations for the transmission line). This is because even though the parameter values were chosen randomly, the distribution is assumed and the model is perfectly deterministic.

The majority of the analysis presented is for a single array. Measurements at 200 mV required the operation of two arrays in series. As a result, we have included an additional uncertainty term for these points that represents the combined effects of the outer dc blocks on the microwave lines and the parasitic capacitance to ground of the isolation amplifiers. Errors due to low-frequency feedthrough in the pulse bias (which can drive the array inductance) are not considered here because such feedthrough is adequately filtered up to 100 kHz (the upper frequency limit of our measurements) by the inner dc blocks. This is confirmed by measurements when the pulse bias amplitude is below the threshold for driving, or pulsing, the Josephson junctions (see e.g., [3, 10]). Although we include discussions of errors due to electromagnetic interference (EMI) and connection repeatability, such errors are not assessed in our overall uncertainty estimates.

5. Type A Uncertainty Analysis

Type A uncertainties for an ac-dc transfer with the ACJVS are predominantly limited by the noise inherent in the transfer standard itself. During ac-dc transfers on the 792A, the dc measurement points often show much more variability than the ac measurement points. Thus, the uncertainties depicted in Table 2 mostly represent the stability of repeated measurements of dc input voltages with the 792A. Deficiencies in the experimental setup (e.g., ground loops, electromagnetic interference) may give the appearance of statistical variability in the ACJVS’ output. Therefore, the user should make every effort to eliminate or account for such effects prior to performing a transfer.

Table 2:

Type A standard uncertainties (k = 1) for AC-DC difference measurements of a 792A thermal transfer standard with the ACJVS. Listed uncertainties are typical. Actual uncertainties will vary with the particular 792A used, as well as the experimental setup. Deviations as large as 30 % from the tabulated uncertainties were found for certain 792A instruments within otherwise identical experimental arrangements.

		Type A Standard Uncertainty of AC-DC Difference, μA / (μV/V)
792A Range (mV)	RMS Voltage (mV)	100 Hz	400 Hz	1 kHz	2 kHz	5 kHz	10 kHz	20 kHz	50 kHz	100 kHz
22	2	62.5	58.9	55.8	64.4	59.8	59.7	57.7	59.0	57.4
22	6	20.2	19.4	18.9	19.3	19.3	19.2	19.3	19.2	19.2
22	10	12.9	12.4	12.2	12.4	12.5	12.5	12.7	12.8	12.6
22	20	6.8	6.6	6.5	6.6	6.6	6.6	6.6	6.6	6.6
220	20	24.7	24.5	22.1	24.6	25.2	25.2	25.8	25.4	25.6
220	60	4.3	4.0	3.2	4.0	4.0	4.0	4.0	4.3	4.2
220	100	2.3	2.0	1.6	2.0	2.1	1.9	2.1	1.9	2.1
220	200	0.93	0.93	0.86	0.95	0.90	0.91	0.91	0.90	0.92

The increased variability observed for dc points can be attributed to the 1/f noise of the thermal sensor and associated electronics within the 792A. The 1/f noise corner frequency varies from unit to unit, but is in the range of 200 Hz down to 2 Hz for the thermal sensor itself. Correspondingly, ac-ac transfers for frequencies above the 1/f corner (e.g., 1 kHz vs 100 kHz) exhibit reduced variability.

5.1. Data Collection and Analysis

In conventional ac-dc difference measurements, δ is defined as,

$${\delta \equiv \frac{Q_{\text{ac}}-Q_{\text{dc}}}{Q_{\text{dc}}}|}_{E_{\text{ac}}=E_{\text{dc}}},$$ (4)

where Q_ac is the ac input quantity (e.g., rms current or voltage) that produces the same response E_dc at the output of the transfer standard as the dc input quantity Q_dc. There are different methodologies to perform the transfer, depending on the accuracy desired and the type of standard under test. One example is the null method, wherein the operator first applies an ac input Q_ac and notes the response E_ac. Next, a positive dc input is applied and then adjusted until the response E_dc+ is equal to E_ac. After achieving a null, the input dc value is then noted as Q_dc+. In order to correct for reversal error and thermovoltages, the last step is repeated with the polarity of the dc input reversed to obtain Q_dc−. Thus, the operator obtains three input quantities: Q_ac, Q_dc+, Q_dc−, such that their respective responses are equal: E_ac = E_dc+ = E_dc−. In this methodology, the dc input reference value is taken to be the mean of the two dc polarities,

$$Q_{\text{dc}}=\frac{Q_{\text{dc}+}+Q_{\text{dc}-}}{2}.$$ (5)

An equivalent relationship is assumed for E_dc. To calibrate a transfer standard in this arrangement requires that either (1) the applied inputs are known (e.g., using an ideal source), or (2) that the transfer standard is calibrated against a reference device with a known ac-dc characteristic (e.g., using a thermal converter).

For the ACJVS, ac-dc difference measurements of the 792A are typically performed using the deflection method. The voltages applied with the ACJVS are known to high accuracy at audio frequencies. Thus, rather than adjust the applied dc voltage to achieve the same output response, the relevant metric is the difference in output response to dc and ac inputs of the same rms amplitude. In order to provide some connection to the conventional definition above for δ, it is assumed that an incremental relative change in the input to a thermal converter produces a proportional relative change in its output [22],

$$\frac{\mathrm{\Delta }E}{E}=n\frac{\mathrm{\Delta }Q}{Q}.$$ (6)

In other words, the response function follows a power law E(Q) = kQⁿ, where k is a constant. We then obtain the following relationship between δ and the output responses,

$$\delta \approx {\delta }_{\text{defl}.}={\frac{E_{\text{dc}}-E_{\text{ac}}}{n{E}_{\text{dc}}}|}_{Q_{\text{ac}}=Q_{\text{dc}}}.$$ (7)

The 792A is sufficiently linear (n ≈ 1) that errors in δ due to residual nonlinearity are correspondingly small. For example, a nonlinearity of 0.5 % (greater than typical) yields a relative error in δ of about the same magnitude, and thus we assume n is unity for measurements of the 792A. For thermal converters, however, 1.6 < n < 2 and it becomes more critical to carefully evaluate n.

In this work, the data used to derive Type A uncertainties were obtained by (1) performing multiple ac-dc transfers at 1 kHz for each voltage and range listed, and (2) multiple ac-ac transfers against 1 kHz for the frequencies and voltages outlined below. The ac-dc and ac-ac measurements were performed in no particular order. But, ac-dc measurements were periodically interspersed over time to check for any long-term drift or otherwise anomalous behavior. Short term drift — that is, statistically significant deviations over timescales comparable to the measurement of each point of an ac-dc transfer — was a feature of most dc measurements. As noted above, such drift is due to the 1/f noise of the 792A’s thermal sensor and input amplifier stages.

The uncertainties in Table 2 represent the average of the daily, pooled sample standard deviation of numerous ac-dc transfer measurements over the course of months on one of NIST’s set of 792A transfer standards. The pooled standard deviation is given by,

$$s_{x,\text{pooled}}^2=\frac{1}{MN-1}\left(\sum _{i=1}^M\left\{(N-1)s_{x_i}^2+N{\overline{x}}_i^2\right\}-MN{\overline{x}}^2\right),$$ (8)

where M is the number of transfers in a given sequence, N is the number of acquired readings of the output voltage of the TTS during each transfer, $s_{x_i}$ and ${\overline{x}}_i$ are the standard deviation and mean, respectively, of the i th transfer, and $\overline{x}$ is the pooled sample mean.

It should be emphasized that we do not use the standard deviation of the mean (or, standard error $SE(\overline{x})$) to represent our Type A uncertainties. This is for two reasons. First, the $SE(\overline{x})$ is an inferential statistic that describes how well the mean $\overline{x}$ of a single sample (of N individuals, or digital multimeter readings) estimates the population mean μ,

$$SE(x)=s_{\overline{x}}=\frac{\sigma }{\sqrt{N}},$$ (9)

where σ is the population standard deviation. While it is true that we are primarily interested in how well our sample mean of δ estimates the true mean, we must first have a reliable value for σ. If σ is not known a priori, then the best estimate is the pooled sample standard deviation. Furthermore, all reported uncertainties would be based upon a particular choice for N, and would need to be scaled to facilitate comparison with other measurements. The pooled sample standard deviation should be approximately fixed for a given 792A, under conditions of repeatability.

Secondly, the representation of uncertainty with the standard error is only valid when the sampling distribution of the transfer means is approximately normal (i.e., when the central limit theorem assumptions are valid). If δ is indeed drifting between transfers, then the underlying population is not stationary and the use of $SE(\overline{x})$ is inappropriate. In ac-dc measurements, deviations from normality in the sampling distribution of transfers may be checked with a sufficiently powerful test, such as the Anderson-Darling test. However, even the most powerful test statistics require many transfers (i.e., M > 50) to facilitate a good decision.

6. Type B Uncertainty Analysis

6.1. Intrinsic errors

Assuming perfect quantization of the input pulse bias sequence, the ACJVS has two instrinsic errors that derive from its basic operating principle as a quantum voltage source. These include phase noise from the pulse pattern generator and the delta-sigma conversion error.

6.1.1. Phase noise

All Josephson voltage standards are based on the inverse Josephson effect, wherein highly accurate time and frequency control is leveraged to generate accurate voltages. Variability in the bias frequency (or pulse density per unit time for the ACJVS) that results from phase noise in the microwave bias electronics will be directly converted into errors in voltage. The phase noise error is typically much smaller than extrinsic systematics for the ACJVS. As a result, our goal here is simply to estimate an upper bound on the phase noise for a typical system. For a more detailed analysis of this topic, the interested reader is referred to the recent study by Donnelly et al. [23].

First, we consider the relative voltage error due to fluctuations in the pulse density p(t),

$$\frac{{\sigma }_V(\tau )}{V(\tau )}=\frac{{\sigma }_p(\tau )}{p(\tau )}={\sigma }_y(\tau ),$$ (10)

where τ is the epoch over which the measurement is completed, the denominators of the left equation are averages over that epoch, and σ_y(τ) is the Allan deviation of fractional frequency fluctuations y = δν/ν₀. The Allan deviation can be estimated by integration of the phase noise spectral density (typically represented as $\mathcal{L}(f)$ in units of [dBc/Hz]) [24, 25],

$${\sigma }_y(\tau )=\frac{4}{{\left(\pi \tau {\nu }_0\right)}^2}{\int }_0^{f_H}10^{\mathcal{L}(f)/10}{\sin }^4(\pi \tau f)df,$$ (11)

where ν₀ is the oscillator frequency at which $\mathcal{L}(f)$ is given, and f_H is an upper frequency cutoff beyond which the phase noise is negligible. For example, since the on-chip filters have a bandwidth on the order of 100 MHz, it is reasonable to assume that f_H ≤ 100 MHz.

Because the instantaneous output voltage of the ACJVS directly depends on the pulse density function p(t), any errors in the relative timing of pulses will lead to errors in voltage, just as with other JVSs. However, for dc, the voltage measurement bandwidth can be made arbitrarily small by sampling for a very long time. For ac waveform synthesis, the bandwidth depends on the transmission line, or at a minimum, on the on-chip filters. Another way to frame the relationship is to ask how well we need to know a particular property of a waveform in the time interval τ? If we are only concerned about the overall rms content of a sine wave, then τ is just an integer multiple of the period of that waveform. In that case, the impact of generator phase noise is quite small indeed. However, if we want an estimate of the waveform’s value at a given instant in time, then τ may approach the limit imposed by the on-chip filters.

With those caveats in mind, we can begin to estimate σ_y(τ). It is assumed that the pattern generator is phase locked to a precision external frequency reference. If the phase-locked loop is functioning properly, the phase noise of the generator should resemble that of the reference, and be flat above about 1 kHz. If we further take the worst case scenario that τ⁻¹ is given by the bandwidth of the on-chip elements (several hundred MHz), then we can work backwards to determine the phase noise performance needed to achieve a given voltage uncertainty at an update rate of about 15 GHz. For a relative voltage error less than 5 parts in 10⁷, the pattern generator needs to have a phase noise better than −150 dBc/Hz, which is not trivial to achieve in practice. However, if our concern is the rms amplitude of a 1 kHz sinusoid, then the relative error falls to 0.2 nV/V with a phase noise of just −120 dBc/Hz.

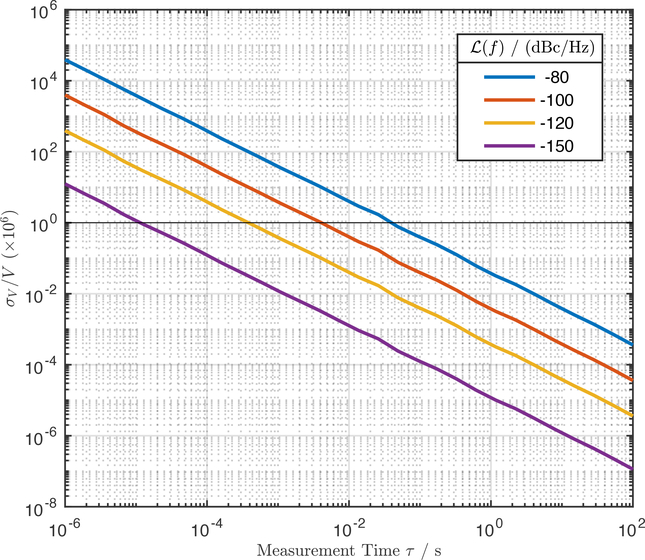
For the purposes of this report, it is assumed that the worst-case uncertainty due to phase noise is 1 nV/V. This value is based on a measurement epoch τ = 30 s and $\mathcal{L}(f)=-80\text{dBc}/\text{Hz}$, independent of frequency. The basis for this decision is that commercially available frequency references are readily available with phase noise lower than $\mathcal{L}(f)=-80\text{dBc}/\text{Hz}$ and the relative contribution to the overall uncertainty for this choice is already negligible. For the reader’s convenience, the 1/τ scaling of σ_V /V for different values of $\mathcal{L}(f)$ is depicted graphically in Figure 3.

Figure 3:

Relative uncertainty in parts per million of the output voltage of the ACJVS due to frequency reference phase noise, in the form of an Allan deviation plot. The curves were generated with the assumption that the one-sided phase noise spectral densities $\mathcal{L}(f)$ are white, with the values indicated in the legend. The horizontal line at 1 μV/V is a guide for the eye.

6.1.2. Delta-Sigma conversion error

A delta-sigma converter takes advantage of oversampling and noise shaping to shift in-band quantization noise power (IQNP) to frequencies outside the band of interest. This is what gives rise to the rapid upward increase of the quantization noise with frequency shown in Fig. 1. The high out-of-band QNP is low-pass filtered by on-chip superconductive filters, and to a lesser extent, frequency-dependent loss in the output transmission line. If the outputs of the Josephson junction arrays are adequately filtered (or the transmission line and/or TTS are themselves band-limited), then the out-of-band QNP will have negligible impact on rms voltage calibrations at audio frequencies.

The delta-sigma conversion error is typically dwarfed by other, external systematic errors. The error for a given delta-sigma pattern is also fully deterministic: in the absence of intentionally added noise (e.g., dithering), the same modulator input parameters (i.e., delta-sigma settings, tone amplitude and frequency) will always yield the same error. So, while it is not possible to predict in advance the error for a given pattern, it can be calculated after synthesis and then used as a correction factor in subsequent measurements. However, if such correction is not performed then the end-user must include the error discussed here as an additional Type B component.

To determine the delta-sigma error, we begin by estimating IQNP of the delta-sigma modulator. The simplest approximation for the delta-sigma modulator is a linearized z-domain model that substitutes the nonlinear effects of the quantizing elements with additive noise. In this linearized approximation, the IQNP for an order L modulator (specifically, the IQNP of its noise transfer function) is given by [6],

$${\sigma }_q^2=\frac{{\pi }^{2L}{\mathrm{\Delta }}^2}{12(2L+1){(OSR)}^{2L+1}},$$ (12)

where Δ is the step size of the quantizer and OSR is the oversampling ratio of the modulator, defined as the ratio of the sampling frequency f_s to the Nyquist frequency 2f_B (twice the specified bandwidth). This formula assumes that f_s >> f_B and that the quantization noise is uncorrelated and its spectrum is white. In the delta-sigma data converter literature, Δ is typically taken equal to 2, in order to have a unity transfer characteristic for a variety of modulator types. For the ACJVS, and a three-level, bipolar pulse pattern (i.e., {−1,0,+1}), Δ is the Shapiro step voltage for the Josephson junction array(s). Note that the IQNP given by the above equation may deviate significantly from the actual IQNP, which can only be obtained by analyzing the spectrum of the generated pulse pattern.

In the convention of Ref. [6], the full-scale range of the quantizer FSR = MΔ, where M is the number of quantizer steps, or increments. The number of quantizer levels is n_lev = M + 1. The peak-to-peak amplitude of an input sinusoid can be expressed in terms of Δ as,

$$V_{\text{pk}-\text{pk}}=k{V}_{\text{FS}}=kM\mathrm{\Delta },$$ (13)

where k is a dimensionless constant between 0 and 1 that represents the amplitude relative to FSR.

The power of the sinusoid is,

$$P_{\text{signal}}=V_0^2=\frac{1}{2}{\left(\frac{kM\mathrm{\Delta }}{2}\right)}^2,$$ (14)

and the signal-to-quantization noise ratio (SQNR) is then,

$$SQNR\equiv \frac{P_{\text{signal}}}{{\sigma }_q^2}=\frac{3k^2(2L+1){(OSR)}^{2L+1}{\left(n_{\text{lev}}-1\right)}^2}{2{\pi }^{2L}}.$$ (15)

As a first, highly-simplified approximation, we assume that the amplitude of the pure tone is reproduced perfectly in the encoded pulse pattern, and that the error in the voltage is due only to the quantization noise in band,

$$V=\sqrt{V_0^2+{\sigma }_q^2}.$$ (16)

The relative rms amplitude error is,

$$\frac{\delta V}{V_0}=\frac{\sqrt{V_0^2+{\sigma }_q^2}-V_0}{V_0}=\sqrt{1+{(SQNR)}^{-1}}-1\approx \frac{1}{2(SQNR)},$$ (17)

assuming of course that SQNR >> 1. Just as the above linear model for the IQNP allows us to derive an upper bound for the achievable SQNR of a second-order modulator, this expression serves as a lower bound on the uncertainty of the encoded tone.

This lower bound is often much, much lower than the actual rms error of a given pulse pattern (the reader is reminded that we are referring here to the error in the digital representation itself, before the pulses ever propagate down the microwave cable). The reason for this discrepancy is that it is not possible to predict a priori the impact of the conversion process on the frequency bin in which the tone resides. In addition to harmonic distortion, noise in the fundamental bin will add directly to the tone, rather than in quadrature. Thus, depending on the transfer characteristic, or the relative phase of the input signal and noise, the signal power in that bin may be slightly lower or higher than desired. The most accurate way to assess this error is simply to encode the pattern in the digital domain and then analyze the resultant pulse pattern. Representative delta-sigma conversion errors are listed in Table 3. Note that the errors are signed, and thus the synthesized voltage may be slightly less than or greater than that desired.

Table 3:

Relative rms voltage error for delta-sigma conversion. Parameters used to derive this table are: Modulator order, 2; Sampling frequency, 14.4 GHz; Number of Josephson junctions, 6400; Bandwidth, 10 MHz; noise transfer function (NTF) maximum out-of-band gain, 1.2. A subset of the NTF zeros were optimized.

RMS Voltage		Frequency
(mV)	(dBFS)	100 Hz	1 kHz	10 kHz	100 kHz	1 MHz
2	−37	4.6 × 10−08	5.1 × 10−08	5.5 × 10−08	2.2 × 10−07	4.4 × 10−06
6	−27	1.8 × 10−09	2.0 × 10−09	4.2 × 10−09	2.0 × 10−07	1.8 × 10−05
10	−23	4.2 × 10−10	5.2 × 10−10	1.8 × 10−09	1.4 × 10−07	1.4 × 10−05
20	−17	5.3 × 10−11	6.9 × 10−11	7.8 × 10−10	6.9 × 10−08	6.8 × 10−06
60	−7.0	2.6 × 10−12	4.2 × 10−12	1.1 × 10−10	9.9 × 10−09	1.0 × 10−06
100	−2.6	7.5 × 10−13	7.0 × 10−13	−3.1 × 10−11	−3.3 × 10−09	−3.4 × 10−07
125	−0.65	4.4 × 10−13	7.9 × 10−14	−6.6 × 10−11	−6.7 × 10−09	−6.7 × 10−07

Finally, although the modulator order can be increased to achieve a smaller error, high-order modulators may become unstable when the out-of-band gain is too high and/or the input signal approaches fullscale. The susceptibility of a modulator to such overloading is also dependent on the waveform applied. There are also practical limitations: (1) high-order modulators require correspondingly longer times to encode the waveforms, and (2) several other ACJVS error sources dwarf the already low rms error obtained with second-order delta-sigma modulators.

6.2. Extrinsic errors

6.2.1. Transmission line response and loading

Transmission line errors are the most significant part of the overall error budget for the ACJVS at frequencies above 10 kHz. At 100 mV and 100 kHz, for example, the deviation from flatness for the probe used in this work is of order 100 μV/V, much greater than a typical multijunction thermal converter (MJTC) uncertainty at the same point.

Unless a correction is made, the operator may choose to simply never use the ACJVS above the audio band, or to only use it at the lowest voltages, where an uncertainty of ±100 μV/V is still lower than the conventional method. Below, we discuss the issues involved with attempting to flatten, or to correct for, the transmission line response, as well as provide estimates for a particular means of correction.

The transmission line comprises on-die elements of the ACJVS chip, wirebonds joining the chip to the carrier, signal traces on the cryopackage’s printed circuit board, the wiring within the dip probe or cryostat, and any external cabling between the ACJVS and the TTS. Furthermore, the observed response of the TTS will depend on its input impedance (about 10 MΩ∥40 pF for the active ranges of the Fluke 792A; the symbol ∥ means “in parallel with”). If additional equipment is connected to the transmission line, this can result in additional loading or stray current injection into the measurement setup. If two or more arrays are series-connected to increase output voltage, then the choice of outer dc block on the microwave bias is also relevant [12]. As a result, the quantum-accuracy that exists on-chip is diminished, and the challenge becomes one of classical transmission line impedance analysis.

Although a Josephson array presents zero source resistance when dc-biased under the critical current threshold, its effective source impedance during waveform synthesis is difficult to analyze because of its nonlinear dependence on many factors, such as the voltage and frequency of the waveform being synthesized, the parameters of the Josephson arrays, and the particular microwave biasing technique being used. A reasonable approximation is to represent the arrays as a series combination of an inductance L and an impedance consisting of the Josephson superconducting element shunted by its normal state resistance R_N. The total inductance is comprised of (in decreasing order of significance): the finite wiring inductance between individual Josephson junctions and between separate arrays, the Josephson inductance, and the kinetic inductance of the supercurrent. For the SNS junctions used in NIST JVS systems, the wiring inductance is approximately 3 pH per junction, while that of the on-chip lowpass filters is in the range of (50 to 100) nH per filter, and there are two such filters per array. As a result, the effective source inductance will be greater for chips with more junctions per array and/or when more arrays are connected in series to increase the overall output voltage.

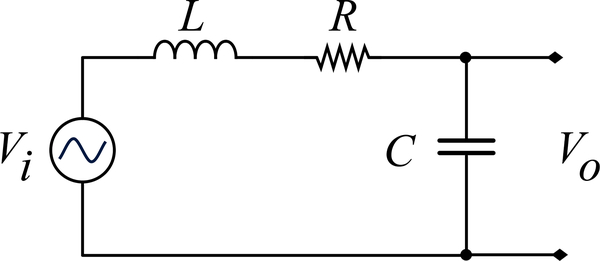
At frequencies such that the wavelength is much longer than the electrical cable length, the transmission line may be crudely approximated as a lumped element RLC circuit. The RLC circuit (cf. Figure 4) is a series connection of R, L, and C, and functions as a lowpass filter (LPF). The transfer function |H(f)| = V_o/V_i for the RLC LPF is second order, and thus its response can be parameterized by the natural frequency,

$${\omega }_0=\frac{1}{\sqrt{LC}},$$ (18)

and the damping parameter,

$$\zeta =\frac{R}{2}\sqrt{\frac{C}{L}}=\frac{R}{2Z_0},$$ (19)

where Z₀ is the characteristic impedance of the transmission line. For our purposes it is the flatness of the response that is relevant, and the maximally flat Butterworth response is obtained when $\zeta =\sqrt{2}$. Although the ACJVS is comprised of one or more distributed transmission lines, the crude RLC approximation serves to qualitatively illustrate the dependence of the line’s response on certain of its parameters.

Figure 4:

Lowpass RLC filter schematic, which may be used as a simplified approximation for the response of the ACJVS transmission line. The input is applied across all three elements and the output is taken across the capacitor C.

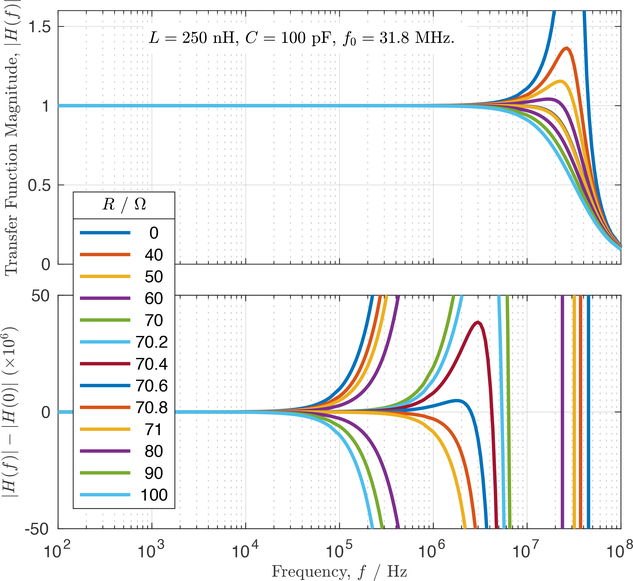
In an effort to flatten the transmission line response, sometimes a series resistance is inserted at some point along the line [4, 10, 14]. However, as depicted in Fig. 5, the flatness of the RLC-approximated line’s response is extremely sensitive to the choice of R. For R = 0, the deviation from a perfectly flat response becomes relatively large: 10 μV/V at around 100 kHz.^¶ If R is carefully chosen to achieve a small ac-dc difference at a high frequency (say 1 MHz for the case in Fig. 5), then the transmission line error at lower frequencies can be reduced. For R less than some threshold value (~ 70 Ω in Figure 5) and for f ≪ ω₀/2π, the response is roughly quadratic and we obtain a reduction in uncertainty as,

$$u\left(f_l\right)\sim {\left(\frac{f_l}{f_h}\right)}^{2}u\left(f_h\right),$$ (20)

where f_l and f_h are the low and high frequencies, respectively⁺. This approximate scaling is also valid for distributed transmission lines when the product of the propagation constant and line length is much less than unity. However, there are drawbacks to this approach. Namely,

Figure 5:

Frequency response of an RLC approximation to a 50 Ω, 1 m long transmission line for selected resistances R. The frequency axis is the same for upper and lower plots.

1. The presence of a relatively large series resistance means that loading effects would be significant. A model would need to be developed in order to make a valid comparison between ac-dc data from conventional calibrations and those with the ACJVS.

2. The presence of a finite R in the ACJVS output circuit will make the measurement setup more susceptible to stray bias currents and to the effects of electromagnetic interference.

3. The sensitivity of the response to the value of R places severe constraints on the characteristics of the passive components, such as parasitic reactances and temperature coefficient. Metal foil surface mount resistors can satisfy some of these requirements, but they are obviously not adjustable. If a trimpot is used, its backlash, stability, and inductance will become limiting factors. While it may be possible to place a metal foil resistor at 4 K that accounts for the majority of R and a trimmer at room temperature, small value trimmers often exhibit poorer characteristics than their high-value counterparts.

4. Even if R could be fashioned with perfect stability, the rest of the transmission line components may vary over time, due to effects such as the liquid helium level (assuming a dip probe is used), connection repeatability, flexure, and changing loads. These effects imply that R would need to be periodically verified and adjusted.

5. This pseudo-matching technique is based on the assumption that we can accurately measure the voltage output at high frequencies. Or, at least accurately compare a voltage at high frequency with that at a lower frequency. In other words, if an accuracy of better than 10 μV/V at 100 kHz is required, then we need a detector that has a traceable flatness better than 0.1%, or 0.01 dB, for frequencies near 1 MHz. Thermal transfer standards are arguably the only devices that can achieve that requirement at that frequency. Thus, this arrangement sets up a circular condition wherein the ACJVS is calibrated with the device it was intended to calibrate.

An alternative approach to reducing the transmission line error involves carefully characterizing its physical properties, such as impedance or the on-chip inductances [11]. The challenge, however, is that much of the transmission line is inaccessible when the chip is cold. Even if good, representative measurements could be performed, there is a limit to the accuracy of such measurements, due to the underlying accuracy of the instrumentation (e.g., LCR meters, impedance analyzers). The best LCR meter uncertainties at audio frequencies for Z ≈ (50 to 100) Ω and L ≈ 100 nH are 0.1 % to 1 %. That is for 4-wire components measured at the front panel of the LCR meter; the addition of adapters or fixtures quickly inflates the uncertainty budget.

Assuming that such an approach is indeed feasible, it is instructive to model the effects of such variability on the transmission line response. Figures 6–8 show the expected response of a composite transmission line model for the ACJVS with uncertainty in the measurement of the in-probe or in-vacuum twisted pair impedance Z and in the on-chip inductance L. The variability of each parameter is modeled in Monte Carlo fashion with values chosen from a normal distribution centered about the nominal value. We used commercial RF simulation software (Mathworks RF Toolbox) to model the entire structure for the composite line, including: (1) intra-array and on-chip filter inductance, (2) series impedance (if applicable), twisted-pair line within the dip probe, (3) coaxial cable outside the dip probe (including common-mode choke), and (4) the input impedance of any connected equipment, such as the TTS. The model accounts for skin effects in the coaxial cable, but not in the twisted-pair line.

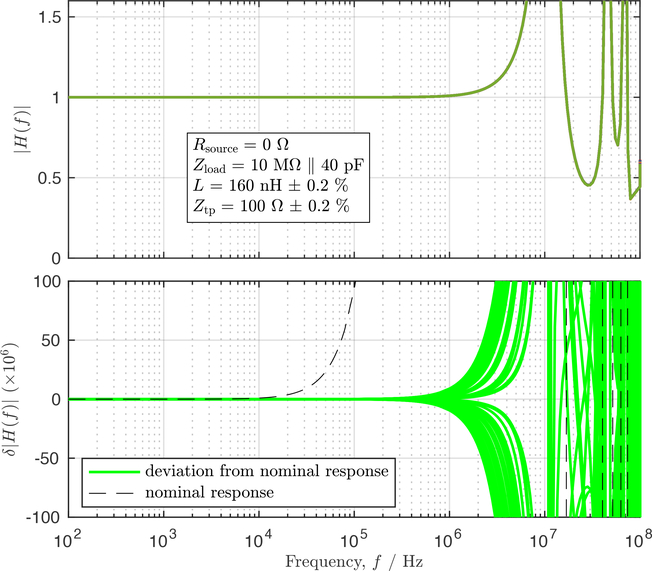
Figure 6:

The frequency response of a composite transmission line model for a single, 6400-junction array of the ACJVS for σ_L = 0.2 % and σ_Z = 0.2 %. Frequency axis is the same for upper and lower plots. The model includes the effects of source resistance (when applicable), on-chip lowpass filters, twisted-pair wire in the probe (1.5 m), coaxial cable outside the probe (1.5 m), and the typical load presented by the Fluke 792A on its active ranges. The top plot shows the overall transfer function of the composite line and the parameters used in the model. The black dashed curve in the bottom plot is the nominal deviation of the response from its value at DC. The remaining solid green curves are deviations from that nominal response due to variability in L and Z. Of the roughly one thousand curves generated, only those that lie within ±1 standard deviation of the nominal response are shown.

Figure 8:

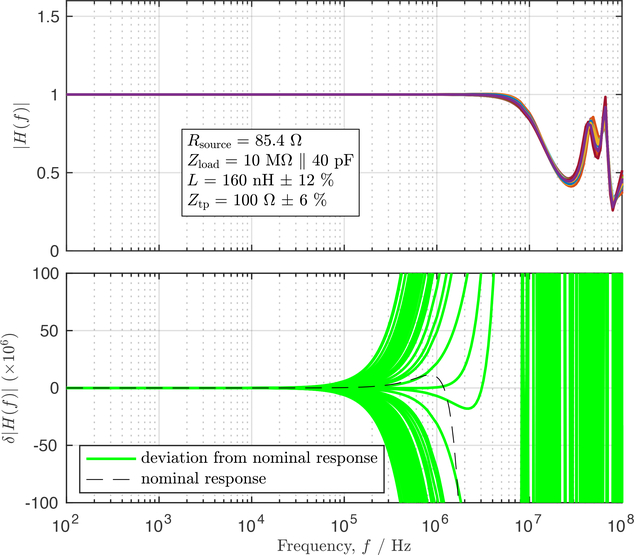
The frequency response of a composite transmission line model for a single, 6400-junction array of the ACJVS with a non-zero source resistance, the value of which is chosen to optimize the flatness of the composite line. σ_L = 12 % and σ_Z = 6 %, as in the previous plot. Model parameters are otherwise identical to those in Fig. 6. Additional details are in the text and the caption for Figure 6.

Figure 6 shows the variability in transmission line response for parameter uncertainties corresponding to measurements at the front panel of a precision impedance analyzer, σ_L,Z = 0.2 % (based on the uncertainty equations given in the user manual for a Keysight E4990A). Note that the uncertainty of the transmission line at 1 MHz is comparable to that for a multijunction thermal converter for voltages at or above 100 mV. This suggests that minimizing the transmission line error at 1 MHz and for ~1 m line lengths to that of thermal converters would place stringent — likely unrealistic — requirements on the characterization of the ACJVS inductance and impedance.

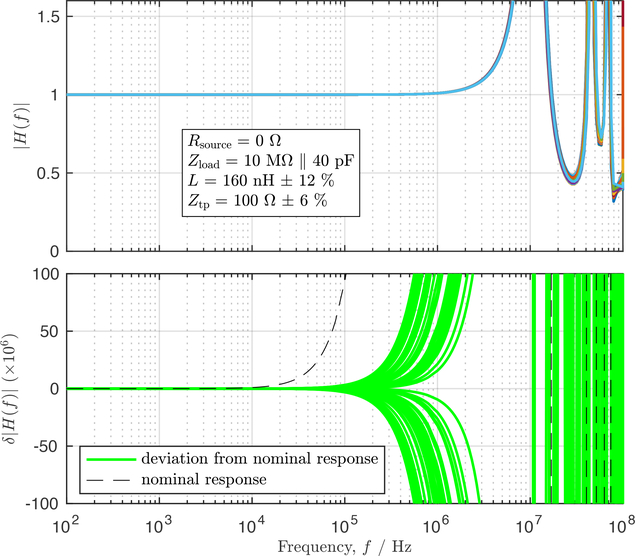
Measurements of a cold dip probe with a 4-terminal pair impedance analyzer (Keysight E4990A) suggest realistically achievable parameter uncertainties of σ_L = 12 % and σ_Z = 6 %. Figure 7 shows the variability in transmission line response corresponding to these relaxed parameter estimates. The roughly 100 μV/V error at 100 kHz can be corrected down toward ±10 μV/V, much closer to that obtained with MJTCs. While the 1 % error at 1 MHz can be corrected down to roughly 350 μV/V, this is still much greater than the 10 μV/V uncertainties (k = 1) attainable with MJTCs.

Figure 7:

The frequency response of a composite transmission line model for a single, 6400-junction array of the ACJVS for σ_L = 12 % and σ_Z = 6 %. Model parameters are otherwise identical to those in Fig. 6. Additional details are in the text and the caption for Figure 6.

As mentioned, the model does not account for skin and proximity effects in the twisted-pair line. Measurements of the copper twisted-pair line indicate that the total inductance changes by about 15 % to 20 % over the range of frequencies accessible with the ACJVS. Furthermore, since the resistivity of copper is temperature-dependent, the temperature distribution of the line (e.g., how much of it is submerged in liquid helium) will influence the spatial distribution and mean of the line’s respective electrical parameters. Comparing measurements of the line at room temperature versus immersion in liquid helium indicate inductance variations of order 10 %, depending on frequency.

Such frequency- and temperature-dependent effects also impact the accuracy with which the on-chip characteristics can be measured in-situ, although they may be partially mitigated through the use of low-RRR (residual resistivity ratio) conductors, such as phosphor bronze. However, as outlined above the finite resistance can create additional measurement challenges.

For the Monte Carlo simulations used in Figures 6–7, we assumed zero additional series impedance in the line (i.e., beyond the small resistance of the copper in the transmission line components). One conjecture is that uncertainties could be improved through a combination of flattening the line response with a series resistor, as well as characterizing elements of the line itself. However, as depicted in Fig. 8, choosing the optimal resistor value (which we have the luxury of doing in a simulation) does not reduce the sensitivity of the response to variability in the line’s elements. This result raises questions about so-called “matching” or “tuning” procedures, such as that in [14]. While the approach outlined in [14] has the advantage of not relying on lumped element approximations, it does not represent a true “impedance matching” procedure because only one component of the complex impedance is being matched. More significantly, however, is that the procedure depends on critically adjusting a series resistor and line length to obtain a cancellation of several terms in the line’s response. If the critically-tuned equation (their Equation A.7) is taken as a starting point for an uncertainty calculation, it will yield unreasonably small uncertainties for this correction. This is because although the terms may cancel perfectly in the response equation, their respective uncertainty contributions do not. The model used in this report fully reproduces the critically-tuned response given in [14], but it goes further by showing that such procedures do not circumvent the critical dependence of the response on the line’s parameters.

6.2.2. Quadrature and compensation bias errors

The cryopackaged die of the ACJVS contains one or more arrays of thousands of Josephson junctions connected in series. Each array exhibits an inductance of tens of nH. Under a current bias, the intra-array inductance may contribute a voltage V_Q that is in quadrature with the desired output tone V as,

$$V_{\text{out}}=\sqrt{V^2+V_Q^2}=\sqrt{V^2+{(\omega LI)}^2},$$ (21)

where ω is the angular frequency of the tone, L is the the array inductance, and I is the current through the array at the frequency ω. It should be noted that this effect is limited to biasing arrangements in which the microwave pulse sequence reaching the array has significant power at the frequency ω, or when a compensation bias is used. If there is no appreciable current flowing through the array at the output tone(s) of interest, the quadrature effect may be disregarded.

For compensation biasing at audio frequencies, the quadrature error is typically less than 0.1 μV/V, which is much less than the typical Type A uncertainties for an ac-dc transfer. However, at higher frequencies the error can become large (e.g., 0.05 μV/V at 100 kHz versus 130 μV/V at 5 MHz). Additionally, since the critical current I_c of the junctions sets the overall scale for the current bias, the quadrature error will be greater for arrays with larger I_c.

The quadrature error may be characterized by analyzing both the in-phase and quadrature components during operation. If such vector-based measurements are done across frequency, then the inductance L can be known to relatively high precision. Likewise, if non-compensated bias arrangements are used, such as with careful shaping of the input microwave pulses, then the quadrature error can be substantially reduced. However, compensation biasing with an additional lower-speed generator is required in order to synthesize the largest rms voltage with the ACJVS. In this situation, phase misalignment between the low-speed generator and the pulse pattern generator can contribute an additional error that is closely related to the quadrature error.

To illustrate, consider the array as a series combination of the ideal Josephson junctions and the array inductance L. If we assume that the compensation generator’s phase is delayed by ϕ (relative to the waveform that is output by the ideal JJ array), then we can rewrite the above equation for V_out as,

$$V_{\text{out}}=\sqrt{V_I^2+V_Q^2}=\sqrt{{(V+\omega LI\sin \varphi )}^2+{(\omega LI\cos \varphi )}^2},$$ (22)

where V_I represents the in-phase component of the measured output tone. If we normalize this expression to the desired output voltage, we obtain an expression for the relative rms error due to the combined effects of array inductance (quadrature) and compensation phase error,

$$u_{\text{quad}/\text{comp}}\equiv \frac{V_{\text{out}}-V}{V}=\sqrt{{(1+\beta \sin \varphi )}^2+{(\beta \cos \varphi )}^2}-1,$$ (23)

where β = ωLI/V. Since the ACJVS waveforms are derived by way of pulse-density modulation, the current I is proportional to the synthesized voltage V,

$$I\sim I_c\frac{V}{V_{\text{fs}}},$$ (24)

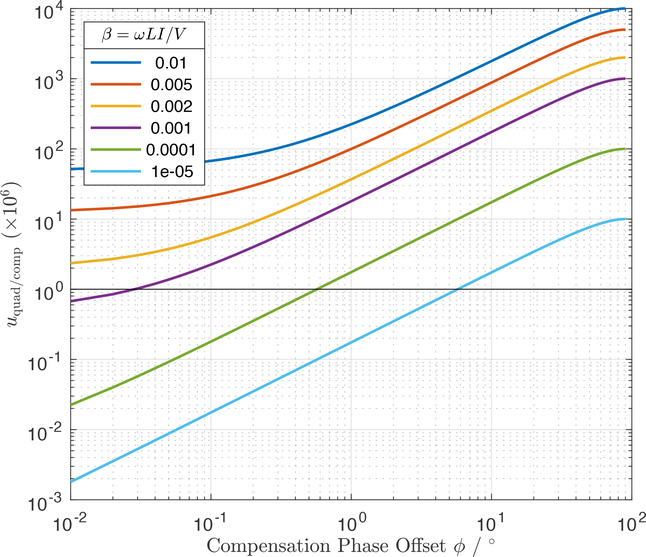
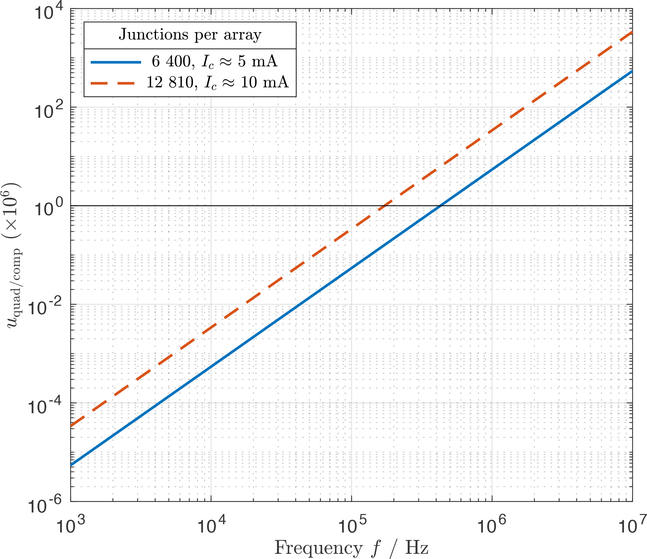
where V_fs is the full scale voltage of the array. We then have β ≈ ωLI_c/V_fs, which only depends on the junction array parameters and the frequency. When cast in this form, it is evident that β is practically always less than unity for realistic device parameters. Furthermore, although the quadrature component itself depends linearly on frequency, its impact will scale quadratically with frequency in ac-dc difference measurements, which depend on the rms content of the waveform. A plot of u_quad/comp vs. ϕ, for different β, is shown in Fig. 9. A plot of u_quad/comp vs. frequency, for specific types of arrays relevant to the NIST ACJVS, is given in Fig. 10.

Figure 9:

Error in the rms output of a single, 6400-junction array of the ACJVS vs. the phase offset between the pulse pattern and the low-frequency compensation bias.

Figure 10:

Error in the rms output of a single array of the ACJVS due to the quadrature error vs. frequency. The horizontal line at 1 μV/V is a guide for the eye.

A potential source of confusion is that the compensation generator phase that maximizes the ACJVS operating margin^* may not necessarily correspond to ϕ = 0 (see, e.g., Section 4.1 of Ref. [4]). However, the correct phase can be obtained accurately by the procedure outlined in [10], or by explicitly measuring the in-phase and quadrature components of the output and maximizing the quadrature part.

As written above, u_quad/comp > 0 when the quadrature error increases the rms voltage from its nominal value. An increasing ac rms amplitude implies a decreasing AC-DC difference δ. Thus, if the quadrature error is small and can be estimated with reasonable precision, the end user may correct for it by simply adding it to the AC-DC difference for the TTS. Such a correction is reasonable when (a) TTS nonlinearity and the net change in rms voltage due to the quad error are sufficiently small that the nonlinear component of the ac-dc difference (voltage coefficient times voltage change) is smaller than u_quad/comp, and (b) the uncertainty in the estimate of u_quad/comp is less than, or approximately equal to, that of the AC-DC difference δ. Under these conditions (and when β or ϕ are both much less than unity), the sensitivity of u_quad/comp to fluctuations in β or ϕ is approximately the same,

$$\frac{\partial u}{\partial \beta }\approx \frac{\partial u}{\partial \varphi }\approx \beta .$$ (25)

From the above we can derive an estimate for the uncertainty of the quadrature error with the usual linear propagation of error methodology,

$${\sigma }_u\approx \beta \sqrt{{\sigma }_{\beta }^2+{\sigma }_{\varphi }^2}.$$ (26)

For example, if β is of order 10⁻³, and the uncertainties for both parameters are of the same order, then the uncertainty of the correction for the quad error is roughly 1 μV/V, which is about the same as the quad error itself, so a correction is not going to be particularly helpful in improving the uncertainty budget. On the other hand, if β is known to a reasonable accuracy (say σ_β/β ≈ 10⁻²), and σ_ϕ can be ignored, then σ_u ≈ 0.01 μV/V, and a correction is warranted.

As mentioned above, a properly-configured bias arrangement will enforce ϕ = 0. However, the compensation generator DAC used in this work is clocked at 100 MSa/s (megasamples per second), and delays are limited to integer multiples of the sample period. As a result, the available phase resolution is highly discretized. For a 1 MHz tone synthesized using a single, 6400-junction array with I_c = 5 mA (β ≈ 0.003), the phase increment will be about 4°. The inability to precisely adjust ϕ translates to an error in u_quad/comp of order 100 μV/V. Unless the vector components of the output waveform are measured, the end user can only assume that the quad error is bounded to within ±100 μV/V.

At high frequencies, the compensation generator’s jitter may also increase the uncertainty in ϕ. However, if the source was manufactured in the last decade or so, an rms jitter less than 10 ps is attainable, which corresponds to σ_ϕ ~ 60 microradians at 1 MHz. Thus, with the exception of hardware-limited phase control, the uncertainty in the quad error will be dominated by the uncertainty in β. When ϕ is indeed zero, β is equal to the ratio of the quadrature and in-phase components of the voltage output by the ACJVS. If these components are measured directly for the purposes of correction, we can re-write the expression for u_quad/comp as,

$$u_{\text{quad}/\text{comp}}=\sec (\theta )-1,$$ (27)

where θ = tan⁻¹(V_Q/V_I). If the phase offset ϕ is nonzero but small, then the deviation from the ideal voltage V cannot be determined unambiguously from measurements of only V_I and V_Q; the phase offset must also be measured. If we assume for now that ϕ = 0, then the uncertainty of the quad correction is approximated by,

$${\sigma }_u\approx \theta {\sigma }_{\theta }.$$ (28)

Thus, the determination of the quad error uncertainty is reduced to estimating θ, or the relative magnitudes of V_I and V_Q. Since operating conditions are often such that V_Q «V_I, the uncertainty of the quad error depends on the nonlinearity and gain error (if not already calibrated) of the device (e.g., digitizer, lock-in amplifier) used to measure the vector components. At 1 MHz, θ ≈ β = 3.3 × 10⁻³, u_quad/comp ≈ 5 μV/V, and if we assume that a total harmonic distortion of −90 dBc for the ADC is a reasonable proxy for its nonlinearity at 1 MHz, then σ_θ ≈ 30 μV/V and thus σ_u ≈ 0.1 μV/V.

In summary, the quadrature error in the ACJVS is sufficiently small (relative to other effects) at audio frequencies that it can be ignored for the majority of ac-dc difference measurements. Starting around 100 kHz, the magnitude of the error approaches 1 μV/V, and so it may be warranted to measure the in-phase and quadrature components of the waveform in order to apply a correction. However, in the majority of scenarios, the transmission line error will exceed that of the combined quadrature/compensation effects.

6.2.3. Thermovoltage errors

Errors arising from thermal electromotive forces (EMFs) are in most cases negligible for ac-dc difference measurements with the ACJVS. However, for completeness we will briefly discuss them here. The thermal noise of the ACJVS is vanishingly small, since the source resistance is small — typically just the series resistance of the transmission line. The noise floor of room-temperature instrumentation will most often be the limiting factor.

However, there will be an additional voltage noise due to fluctuations of thermal EMFs in the transmission line, since it spans the temperature gradient between 4 K and 300 K. A constant thermovoltage will be automatically corrected for as a result of the way ac-dc transfers are performed. But, the dc+ and dc− voltages are measured at different instances in time, and if these times are well separated, then drift in the thermovoltage can contribute a small error to the ac-dc difference.

This error can be quantified by connecting a nanovoltmeter to the output of the ACJVS and measuring the instantaneous voltage with the ACJVS off. Typical values for the mean thermovoltage for a dip probe are (10 to 100) nV, with rms fluctuations of about (10 to 20) nV. However, these can be larger if the transmission line wiring is not optimized for these effects, or if the wiring within the ACJVS was not completely thermally stabilized (e.g., starting measurements soon after the dip probe or cryostat are cooled). Estimates for the uncertainty contribution of such fluctuations are given in Table 6.

Table 6:

Errors due to thermovoltage uctuations in units of μV/V. The values listed assume an rms thermal noise voltage V_th = 20 nV, which should not depend strongly on the details of the experimental configuration. Note that this error only impacts dc and very low frequency measurements. It should not be included in the uncertainty for AC-AC transfers at frequencies well above 10 Hz.

RMS Voltage (mV)	Thermovoltage Error Vth = 20 nV (μV/V)
2	10
6	3.3
10	2
20	1
60	0.3
100	0.2
200	0.1

6.2.4. Electromagnetic Interference: Ground loops and common mode noise

In many precision metrological applications, it is advantageous or simply mandatory that the measurement apparatus be isolated from interference originating from external equipment. Electromagnetic interference (EMI) may couple into a system capacitively via unshielded cabling or ungrounded/floating instrumentation. EMI may also couple inductively if ground loops are inadvertently created through the use of unoptimized wiring routes.

Given the intricate biasing arrangement of the ACJVS, there are numerous experimental setups that may result in difficult-to-detect systematic errors. Here, we enumerate the details of one particular setup using the equipment outlined in Table 1 that has (after many iterations) shown itself to be optimal for ac-dc transfer measurements. Even so, the reader is cautioned that the performance of this configuration may improve or degrade, depending upon how significantly future ACJVS-specific hardware deviates from that described in this report. For this reason, and the fact that the relative contribution of such EMI-induced errors depend on the specific value for δ, we do not include such errors in our overall uncertainty budget.

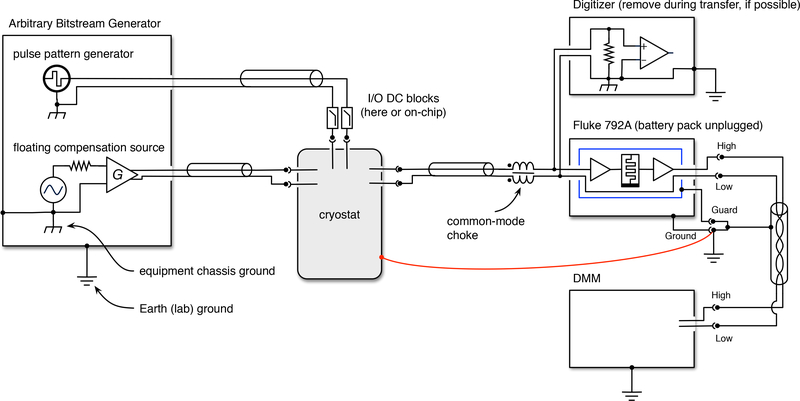
The configuration used for this report is depicted in Fig. 11, and may be summarized as follows:

1. A single, EMI-filtered power strip is attached to the equipment rack and powers the pattern generator, PXI chassis (containing digitizer, etc.), and digital multimeter (DMM) for measuring the output of the 792A. The power strip serves as the primary grounding point in our configuration.

2. The pattern generator is connected to the controlling computer via an unshielded ethernet cable through a network switch. Since the termination points of the ethernet connection are already balun-isolated, there is no need to use optical links or media converters. In fact, the switching power supplies of the media converters are often a significant source of EMI, unless they are placed as far as possible from the ACJVS.

3. When needed, external baluns are used to break ground loop and common mode loop coupling that may occur in the distribution of the 10 MHz reference clock. As noted above, for certain instrumentation the baluns are internal.

4. The PXI chassis containing the NI 5922 digitizer is connected to the computer via an optical link. The digitizer input is typically configured as “single ended”, which means the shell of the BNC connector is grounded to the chassis. The DMM for measuring the 792A output, which is also under computer control, is likewise galvanically isolated from the computer.

5. Battery-powered isolation amplifiers are used between the pattern generator compensation outputs and the cryostat/dip probe. The amount of isolation is primarily determined by the input bias resistors of the amplifiers, typically 1 MΩ to 10 MΩ at dc. The isolation vs frequency of these amplifiers was measured and corresponds to a capacitance of order 40 pF.

6. The guard terminal of the 792A is shorted to its ground at the banana jacks near the output terminals. The low terminal of the 792A is not connected to guard or ground. The ground of the 792A is then tied back to the power strip.

7. A common mode choke, comprised of a 46 cm length of coaxial cable threaded several times through a toroidal, high-permeability core, is inserted between the output of the dip probe and a BNC tee connector, which is in turn connected to the input of the 792A.

8. The output of the 792A is connected to the DMM via a shielded, twisted pair cable. The shield of that cable is grounded at the 792A end to the 792A ground; the shield is not connected to the DMM.

9. The other port of the tee mentioned in Item vii is connected to the digitizer with a 46 cm coaxial cable. This cable is disconnected at the tee during ac-dc transfers.

10. For cryopackages that do not have on-chip inner/outer DC blocks, all input/output ports of the dip probe are isolated from the probe body (e.g., using isolated ground panel-mount feedthroughs). The body of the probe and the dewar are all grounded to the 792A ground. Inner/outer DC blocks (f_c ≈ 500 MHz) are inserted between the microwave feedthroughs at the dip probe and the microwave cabling from the bitstream generator.

Figure 11:

Simplified schematic of the ACJVS grounding arrangement.

When attempting to troubleshoot EMI-related problems, one should keep in mind that established techniques used to isolate equipment at dc are not necessarily good ac techniques. When floating equipment on batteries, the ungrounded metal components become effective entry points for broadband noise and the impact of this noise on measurements will depend on the physical arrangement of nearby equipment and cabling. From the standpoint of repeatability and reproducibility, it is preferable to establish a well-defined ground, as well as the impedances between signal leads and that ground.

The internal guard of the 792A affords some protection from high-frequency common mode noise^♯. But, it can be easily defeated if other equipment without such protection is connected to the measurement network. For example, if the digitizer is powered from the mains and connected to the 792A, then the low terminal becomes grounded and the voltage measurement is effectively single-ended. If instead the digitizer is powered from a battery, then the digitizer chassis and the additional cabling increase the susceptibility of the system to common mode noise through stray capacitance to ground.

Because the 792A responds to frequencies well beyond its specified 1 MHz limit (its −3 dB bandwidth is around 10 MHz, depending on input range), it is preferable to disconnect the digitizer prior to performing a transfer (once ACJVS operating margins have been established). Ideally, the disconnection point should be as close as possible to the transfer standard, so as to minimize the overall length of the transmission line (cf. Item ix in the list above). In situations where the digitizer must be spliced into the network (e.g., for automation), a common-mode choke, or current equalizer, is usually required to obtain repeatable results.

In alternate ACJVS configurations with relatively short transmission lines (< 0.5 m) and without the digitizer connected, the author has found that common-mode noise is sufficiently small that the choke is unnecessary. This is important because the effective length of the transmission line depends on whether or not a choke is inserted into the network. The impact of the choke on the line’s response at 1 kHz is negligible, but may be significant at high frequencies. For this report, we do not consider this interaction directly since we used a choke for all experimental results, and assumed a choke was present in the simulations for the transmission line in Section 6.2.1.

Measurements of the 792A’s response to common-mode noise arising from the ACJVS network are shown in Table 7. The large shifts in the 792A’s output voltage, depending on whether the common-mode choke is present, suggest that there is significant broadband, common-mode noise on the output leads of the ACJVS. Note that this noise is not due to the rapidly rising noise floor of the delta-sigma conversion, because shifts of a similar scale are observed when the ACJVS is not running (but still connected to the 792A). The broadband rms magnitude of the common mode noise is estimated from spectral measurements to be of order 1 mV without the choke and of order 100 μV with the choke.

Table 7:

The effect of common-mode noise on the measured output of the 792A thermal transfer standard for a 1 kHz sinusoidal input. The presence of the choke changes the effective transmission line length, but the change in the line's response at 1 kHz is negligible compared to the observed shifts in output voltage. Additional details are given in the main text.

RMS Input (mV)	792A Range (mV)	792A Voltage	Output (V)	Relative Shift (μV/V)
		with choke	without choke
20	22	1.829103	1.835400	3443
100	220	0.908186	0.908371	204
200	220	1.816520	1.816615	52

Fortuitously, errors arising from common-mode noise largely cancel out because the noise is present for every voltage of an ac-dc transfer measurement. If the TTS is sufficiently linear, then the presence of large broadband noise simply shifts the operating point of the transfer. There is a limit to this, of course — at the lowest voltages the common mode noise is of the same order as the signal itself. Based on measurements at audio frequencies, it is estimated that EMI-induced errors affect the ac-dc difference at a level below 1 % — even at the lowest voltages. In other words, an EMI-related error would shift the measured value of δ by less than 1 %. The corresponding errors are given in Table 8.

Table 8:

Estimated errors due to common-mode noise. The common-mode noise is assumed to be broadband and its rms amplitude nearly constant, and so will add in quadrature with the primary tone. As a result, the error scales with the value of the ac-dc difference δ, and so the uncertainty is expressed relative to δ. The two columns for the common-mode error correspond to the effective broadband voltage noise with and without the common-mode choke in the transmission line.

	Common Mode Error (% of δ)
RMS Voltage (mV)	Vn = 100 μV	Vn = 1 mV
2	0.25	20
6	0.03	2.7
10	0.01	1.0
20	2.5 × 10−3	0.25
60	2.8 × 10−4	0.03
100	1 × 10−4	0.01
200	2.5 × 10−5	2.5 × 10−3

6.2.5. Connection repeatability

In addition to exercising the usual care when handling RF connectors, the impact of connector loss and repeatability should be considered during calibration with the ACJVS. Unfortunately, connector repeatability data in the span of audio frequencies, or even from 100 kHz to 10 MHz, is not readily available. In order to estimate this effect, one may perform a statistical analysis of many ac-dc transfers in which the cable’s orientation is reversed between transfers.

Although not included as part of our overall uncertainty estimates, an example of such an analysis is provided in Table 9 for an rms voltage of 200 mV. It is instructive to compare the magnitude of the measured reversal error against the Type A uncertainty u_1σ of the sampled dataset for δ. At each frequency the observed reversal error is comparable to the statistical uncertainty of the measurement itself. At larger voltages or smaller load impedances, the effect may become more pronounced.

Table 9:

Observed errors due to reversing the cable orientation between the ACJVS and the Fluke 792A thermal transfer standard between measurements. Although by no means rigorous, such errors may be used to provide qualitative estimates of connection repeatability. Applied rms voltage was 200 mV and transfer standard input range was 220 mV. An RG-58 coaxial cable (30.5 cm length, BNC-type connectors) was used to connect the transfer standard to the output of the ACJVS.

	Cable Forward		Cable Reversed
f	δ (μV/V)	u1σ (μV/V)	δ (μV/V)	u1σ (μV/V)	Rev. Error (μV/V)	Rel. Rev. Error (%)
100 Hz	12.50	0.07	12.44	0.13	0.06	0.47
1 kHz	5.25	0.09	5.25	0.09	0.00	−0.04
10 kHz	−7.92	0.10	−7.69	0.12	−0.24	3.01
100 kHz	−122.93	0.33	−122.78	0.29	−0.15	0.12
1 MHz	−10776	15	−10792	37	16	−0.15

7. Uncertainty Summary

A representative uncertainty budget for V = 100 mV and f = 100 kHz is provided in Table 10. The combined uncertainty is the root-sum-square of the individual error contributions. Type B uncertainty matrices are presented in Tables 11 (uncorrected) and 12 (corrected). These latter tables give a clearer picture of the underlying systematic errors of the ACJVS before being combined with the Type A uncertainties obtained when measuring the TTS. Corresponding combined uncertainties for calibration of a Fluke 792A transfer standard with the ACJVS are given in Tables 13 and 14.

Table 10:

Uncertainty budget for V = 100 mV and f = 100 kHz, based on the single-array, 6400-junction model. Since the Δ∑ error can be estimated with very high precision, it is not included in the corrected budget. The difference in the assigned uncertainties for the transmission line and quadrature errors are based on the discussion in 6.2.1 and 6.2.2. As discussed in 4, the following sources are not included in the overall uncertainty budget: low-frequency pulse bias feedthrough, electromagnetic interference, and connection repeatability.

	Standard Uncertainty (k = 1) / μV/V
Error Contribution	V = 100 mV, f = 100 kHz
	Uncorrected	Corrected
Δ∑ conversion	0.003	—
Phase noise	0.001	0.001
Transmission line	93.4	3
Quadrature error	2.1	0.003
Thermovoltage uctuations	0.2	0.2
Transfer measurements (Type A)	2.1	2.1
Overall, combined(k = 2)	187	7

Table 11:

Uncorrected, expanded (k = 2) Type B uncertainty matrix for the ACJVS. Values represent the combined errors due to: transmission line, quadrature/compensation, delta-sigma conversion, and phase noise. Note that two, 6400-junction arrays are required to produce 200 mV. For those points, an additional error contribution is included due to the parasitics related to the outer dc blocks and the isolation amplifiers.

	Uncorrected Type B Standard Uncertainty, uB / (μV/V)
RMS Voltage (mV)	100 Hz to 2 kHz	5 kHz	10 kHz	20 kHz	50 kHz	100 kHz	1 MHz
2	20	20	20	21	51	188	18844
6	7	7	7	10	47	187	18844
10	4	4	4	8	47	187	18844
20	2	2	3	8	47	187	18844
60	0.7	0.8	2	8	47	187	18844
100	0.4	0.6	2	7	47	187	18844
200	0.2	0.8	3	12	77	307	31123

Table 12:

Corrected, expanded (k = 2) Type B uncertainty matrix for the ACJVS. Values represent the combined errors due to: transmission line after determination of the characteristic impedance Z_tp and on-chip inductance L (cf. 6.2.1), and phase noise. Note that two, 6400-junction arrays are required to produce 200 mV. For those points, an additional error contribution is included due to the parasitics related to the outer dc blocks and the isolation amplifiers.

	Corrected Type B Standard Uncertainty, uB / (μV/V)
RMS Voltage (mV)	100 Hz to 10 kHz	20 kHz	50 kHz	100 kHz	1 MHz
2	20	20	20	21	687
6	7	7	7	9	687
10	4	4	4	8	687
20	2	2	3	7	687
60	0.7	0.7	2	7	687
100	0.4	0.5	2	7	687
200	0.2	0.6	3	14	1410

Table 13:

Combined, expanded (k = 2) uncertainty for calibration of a Fluke 792A thermal transfer standard with the ACJVS. Values represent the combined errors due to: Type A uncertainties from measurement and estimated Type B uncertainties when no correction is applied. Note that two, 6400-junction arrays are required to produce 200 mV. For those points, an additional error contribution is included due to the parasitics related to the outer dc blocks and the isolation amplifiers.

		Uncorrected, Combined Standard Uncertainty, uC / (μV/V)
792A Range (mV)	RMS Voltage (mV)	100 Hz	400 Hz	1 kHz	2 kHz	5 kHz	10 kHz	20 kHz	50 kHz	100 kHz
22	2	127	119	113	130	121	121	117	128	220
22	6	41	39	38	39	39	39	40	61	191
22	10	26	25	25	25	25	25	27	53	189
22	20	14	13	13	13	13	14	15	49	187
220	20	49	49	44	49	50	50	52	69	194
220	60	9	8	6	8	8	8	11	47	187
220	100	5	4	3	4	4	4	9	47	187
220	200	2	2	2	2	2	4	12	77	307

Table 14:

Combined, expanded (k = 2) uncertainty for calibration of a Fluke 792A thermal transfer standard with the ACJVS. Values represent the combined errors due to: Type A uncertainties from measurement and estimated Type B uncertainties when the correction described in 6.2.1 is applied. Note that two, 6400-junction arrays are required to produce 200 mV. For those points, an additional error contribution is included due to the parasitics related to the outer dc blocks and the isolation amplifiers.

		Corrected, Combined Standard Uncertainty, uC / (μV/V)
792A Range (mV)	RMS Voltage (mV)	100 Hz	400 Hz	1 kHz	2 kHz	5 kHz	10 kHz	20 kHz	50 kHz	100 kHz
22	2	127	119	113	130	121	121	117	120	117
22	6	41	39	38	39	39	39	39	39	40
22	10	26	25	25	25	25	25	26	26	26
22	20	14	13	13	13	13	13	13	13	15
220	20	49	49	44	49	50	50	52	51	52
220	60	9	8	6	8	8	8	8	9	11
220	100	5	4	3	4	4	4	4	4	8
220	200	2	2	2	2	2	2	2	4	14

Reasonable agreement is found when comparing the overall uncertainties tabulated here with ac-dc calibrations and intercomparisons of the Fluke 792A with the ACJVS. For example, the uncertainties presented here for 100 mV and 10 kHz (4 μV/V, k = 2, regardless of correction) are in line with that reported in [16, 11, 17, 18] (5 to 7) μV/V, k = 2. For the same voltage, but at 100 kHz, the corrected uncertainty (7 μV/V, k = 2) is slightly lower than, but still in rough agreement with, other experimental results in which a correction was applied [4, 18] (9 to 16) μV/V, k = 2.

Recent results using a cryostat with a short transmission line (approximately 70 cm) showed a flatness deviation of 510 μV/V at 1 MHz [13], which is much smaller than the typical 1 % deviation obtained with dip probes (no compensation bias was used, so the output voltage was limited to 20 mV). However, according to table 4, significant improvements can still be obtained for conventional dip probes by performing the corrections outlined in 6.2.1, with a post-correction uncertainty of about 350 μV/V at 1 MHz (k = 1). Although this is still much larger than what can be obtained using MJTCs for 100 mV (11 μV/V, k = 1), it suggests that the combined strategies of shortening the transmission line and improving its parameterization may increase the usable upper frequency range of the ACJVS in the future.

Table 4:

Transmission line systematic errors for a single, 6400-junction array of the ACJVS and a transmission line analysis based on the composite model discussed in the text. Uncorrected values represent the deviation from a perfectly at response (|H(f)| = 1) for the chosen nominal parameters: R_source = 0 Ω, Z_load = 10 MΩǁ40 pF, L = 160 nH, Z_tp = 100 Ω, and l_tp = l_coax = 1.5 m. The corrected values represent 1σ uncertainties after a realistic correction based on that nominal response has been applied. A “0” indicates that the actual value is less than 0.001 μV/V.

Frequency	Uncorrected (μV/V)	Corrected, uL = 12%, uZ = 6% (μV/V)
100 Hz	0	0
400 Hz	0.001	0
1 kHz	0.009	0
2 kHz	0.037	0.001
5 kHz	0.23	0.01
10 kHz	0.93	0.03
20 kHz	3.7	0.1
50 kHz	23	0.8
100 kHz	93	3.4
1 MHz	9400	344

8. Conclusion

A detailed uncertainty analysis for ac-dc difference calibrations with an ACJVS was developed and presented. The tabulated uncertainties were compared against prior calibrations and intercomparisons involving the ACJVS, and good agreement was obtained for most of the parameter space explored.

Type B uncertainties for the ACJVS suggest that, compared to conventional calibrations based on MJTCs, substantial improvements in ac-dc measurement uncertainty can be obtained for low voltages in the audio band, without applying corrections. Modest uncertainty reductions can be obtained up to 100 kHz if a reasonably accurate assessment of transmission line parasitics is available. For frequencies well above several hundred kilohertz, the results suggest that uncertainty reductions are unlikely without major modifications to, or painstaking characterization of, both the on-chip elements and the transmission line parameters.

Table 5:

Quadrature/compensation systematic errors for a single, 6400-junction array of the ACJVS. The “DAC-Limited Phase” column refers to the case when the compensation phase resolution is limited by the DAC sample period. Here, a sampling frequency of 100 MSa/s is assumed. The “Intrinsic” column is the residual quadrature error when compensation phase alignment is perfect (i.e., ø = 0, as defined in the text). The “Measured, Corrected” column assumes that ø = 0 and that the vector components of the output waveform have been measured with a spectrum analyzer or digitizer with performance comparable to the NI 5922. The values in this column are the 1σ uncertainties in the ac-dc difference due to the quad error after the correction is applied. A “0” indicates that the actual value is less than 0.001 μV/V.

		Relative RMS Error, uquad/comp / (μV/V)
Frequency	$\mathit{\beta }=\frac{\mathit{\omega LI}}{\mathit{V}}$	DAC-Limited Phase	Intrinsic	Measured, Corrected
5 kHz	1.6 × 10−05	5.3 × 10−03	0	0
10 kHz	3.3 × 10−05	0.021	0	0
20 kHz	6.6 × 10−05	0.085	2.2 × 10−03	0
50 kHz	1.6 × 10−04	0.53	0.014	1.2 × 10−03
100 kHz	3.3 × 10−04	2.1	0.054	2.9 × 10−03
1 MHz	3.3 × 10−03	210	5.4	0.10