Figure 1.

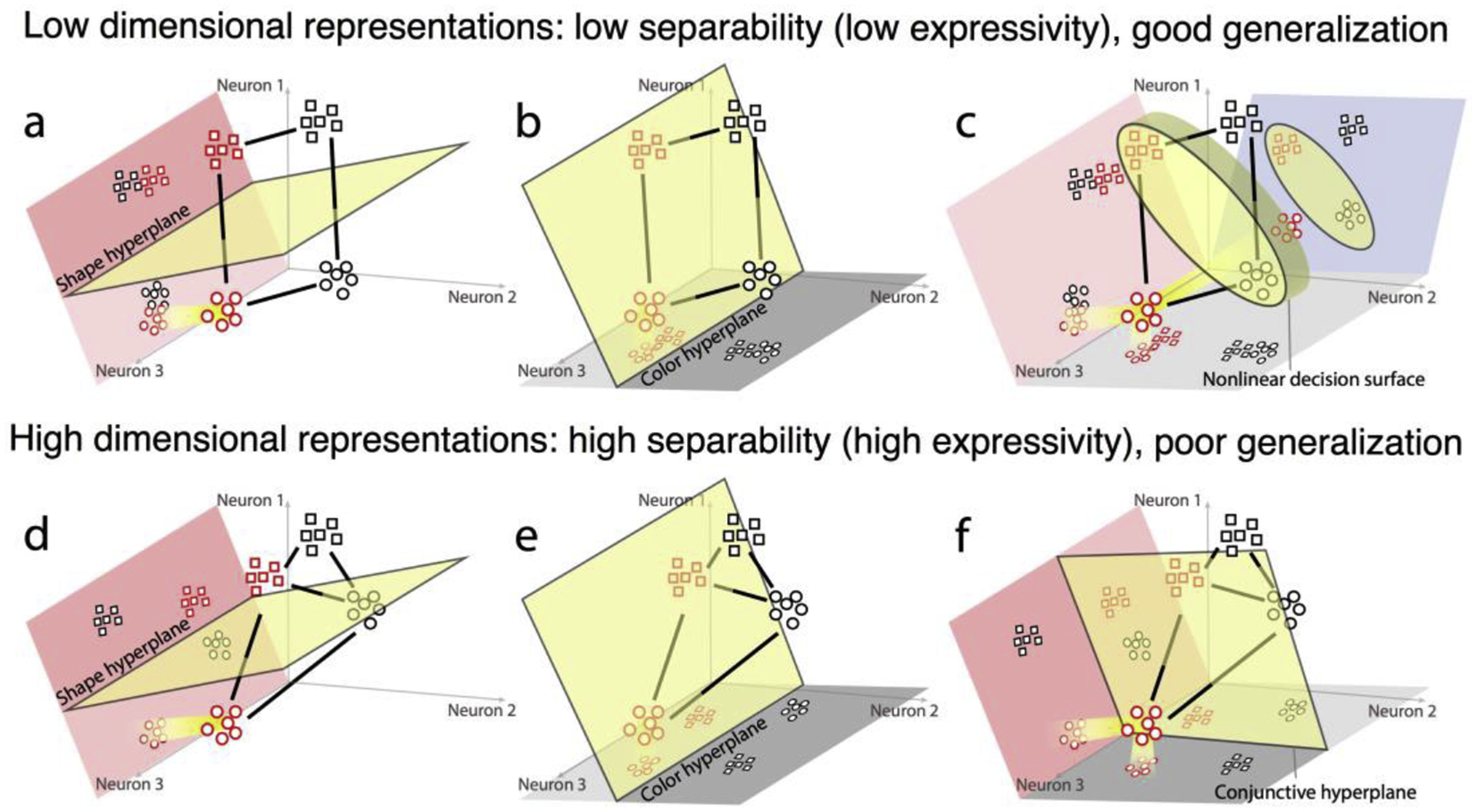
Schematic illustration of representational dimensionality and its computational properties. Each panel plots the response of a toy population of three neurons to stimuli that vary in shape (square or circle) and color (red or black). Axes represent the firing rates of single neurons and collectively define a multi-dimensional firing rate space for the population. Each point within this space represents the population response (i.e., activity pattern) for a given input (identified by colored shapes). Distance between points reflects how distinct responses are, and the jittered cloud of points reflect the trial-by-trial variability in responses to a given input. (a-c) show a low dimensional representation. Though the population is 3-dimensional (i.e., has three neurons), the representation defined by the population responses to the four stimuli defines a lower 2-dimensional plane (traced by solid black lines). A linear ‘readout’ of this representation is implemented by a ‘decision hyperplane’ (yellow) that divides the space into different classes, such as color and shape. The readout can be visualized by projecting (highlighted for red circles) the responses into a readout subspace. (a) In the shape subspace (peach), square and circle stimuli produce distinct, well-separated responses that generalize over different colors. (b) The color subspace (grey) separates red and black but generalizes over shape. (c) illustrates that it is impossible to linearly read out integrated classes (like red-square or black-circle vs black-square or red-circle) in this low-dimensional representation. A non-linear decision surface is required. This problem can be solved by a high-dimensional representation where the response patterns span 3 dimensions (d-f). As before, shape (d) and color (e) information can be linearly read out, though with poorer generalization along the irrelevant dimensions (reflected in the distance between clouds in the irrelevant dimension). Importantly, classes based on color-shape conjunctions (f) can also be linearly read out. Thus, high-dimensional representations are more expressive, making a wider variety of classes linearly separable. A population with a diversity of non-linear mixed selective neurons will have a higher representational dimensionality.