Official websites use .gov
A
.gov website belongs to an official
government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you've safely
connected to the .gov website. Share sensitive
information only on official, secure websites.
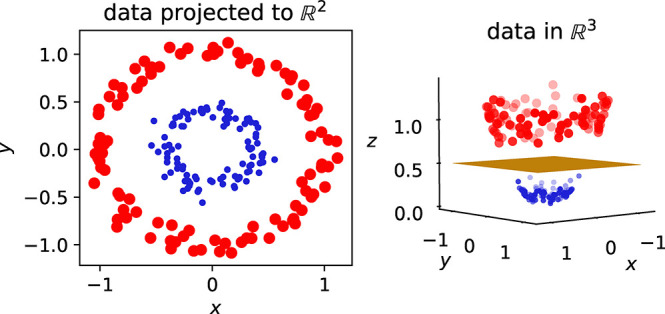
Visualization of one idea behind the kernel trick—mapping to higher-dimensional spaces to make problems linearly separable. In two dimensions, the data (two different classes, colored in red and blue, respectively) are not linearly separable, but after applying the kernel K(x,y) = x·y + ∥x∥2 = ∥y∥2, we can draw a plane to separate the classes (three-dimensional plot on the right).
