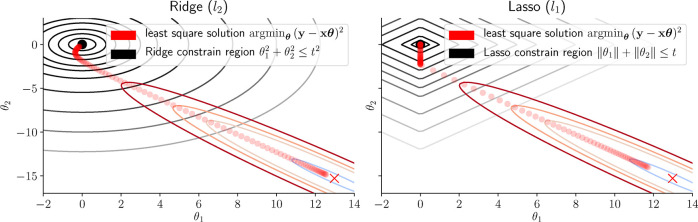
Figure 30.

Visualization of the l₁ and l₂ constraints and the solution paths. The solution (dots) of the constrained optimization is at the intersection between the contours of the least-squares solution (red/blue colored ellipses indicating with the color the error for different parameter choices) and the regularization constraint region (black), which extent depends on λ ∝ 1/t. For λ = 0, we recover the least-squares solution; for λ → ∞, the solution will lie at (0,0). If we increase λ, the optimal solution will tend to be zero in one dimension at the vertex of the LASSO constrain region. For the ridge case, the smooth constrain region will lower the magnitude of the weights but will not force them to exactly zero. Figure created based on an illustration in Tibshirani, Friedman, and Tibshirani³¹ and code by Sicotte.³⁴⁰