Abstract
A key feature of living tissues is their capacity to remodel and grow in response to environmental cues. Within continuum mechanics, this process can be captured with the multiplicative split of the deformation gradient into growth and elastic contributions. The mechanical and biological response during tissue adaptation is characterized by inherent variability. Accounting for this uncertainty is critical to better understand tissue mechanobiology, and, moreover, it is of practical importance if we aim to develop predictive models for clinical use. However, the current gold standard in computational models of growth and remodeling remains the use of deterministic finite element (FE) simulations. Here we focus on tissue expansion, a popular technique in which skin is stretched by a balloon-like device inducing its growth. We construct FE models of tissue expansion with various levels of detail, and show that a sufficiently broad set of FE simulations from these models can be used to train an accurate and efficient multi-fidelity Gaussian process (GP) surrogate. The approach is not limited to simulation data, rather, it can fuse different kinds of data, including from experiments. The main appeal of the framework relies on the common experience that highly detailed models (or experiments) are more accurate but also more costly, while simpler models (or experiments) can be easily evaluated but are bound to have some error. In these situations, doing uncertainty analysis tasks with the high fidelity models alone is not feasible and, conversely, relying solely on low fidelity approximations is also undesirable. We show that a multi-fidelity GP outperforms the high fidelity GP and low fidelity GP when tested against the most detailed FE model. In turn, having trained the multi-fidelity GP model, we showcase the propagation of uncertainty from the mechanical and biological response parameters to the spatio-temporal growth outcomes. We expect that the methods and applications in this paper will enable future research in parameter calibration under uncertainty and uncertainty propagation in real clinical scenarios involving tissue growth and remodeling.
Keywords: Machine learning, Tissue mechanics, Tissue expansion, Skin mechanics, Uncertainty analysis
Introduction
Living tissues remodel and grow in response to mechanical cues. This response can be detrimental, which is common in diseases such as heart fibrosis and dilation following infarct [1, 2], but it can also be leveraged for medical treatment. A prime example is tissue expansion [3, 4]. In this technique, a balloon-like device is inserted subcutaneously and inflated gradually, stretching the skin and inducing its growth [5]. Newly grown skin created with this method is used to design flaps to resurface large defects [6]. Even though the tissue expansion process has gained popularity in reconstructive surgery for its unique capacity to create new skin that is equally functional to native tissue, we still lack predictive capability of how skin adapts to mechanical cues [7]. As a consequence, treatment plans for tissue expansion still heavily rely on surgeon’s training and experience rather than aided by predictive models.
Our need for quantitative knowledge of skin’s response to stretch is part of a broader quest to fundamentally understand the mechanical adaptation of soft tissues [8]. In response to this need, computational modeling of growth and remodeling of living matter has advanced tremendously in the last two decades [9, 10]. One common approach is to describe growth within a continuum mechanics framework through the multiplicative split of the deformation gradient [11]. The split into growth and elastic contributions isolates the two processes kinematically. The evolution of the growth tensor is prescribed with phenomenological equations that aim at capturing essential features of the underlying biological process [12]. The elastic tensor, on the other hand, dictates the stress field through an appropriate constitutive equation describing the tissue mechanical behavior. This approach has been used for a plethora of examples, including the skin, but also valve leaflets, the heart, arteries, and the brain, to name a few applications [13, 14, 15, 16]. The theoretical framework has been extremely successful in isolating key features of the growth and remodeling process. At the same time, the maturation of this methodology to the point at which it can guide medical treatment still requires overcoming some longstanding challenges. One open question is to incorporate the role of inherent variability in biological response and tissue mechanical properties on the corresponding probability of the spatio-temporal growth and remodeling outcome [17]. The current paradigm relies on detailed finite element (FE) models with deterministic parameters adjusted based on some combination of experimentation and parameter sensitivity analyses [18]. This is not enough for decision making in the clinic. At the other end of the spectrum, fully personalized FE methods, such as [8], are also unpractical if not unfeasible at scale.
A recent explosion of data-science and machine learning methods has started to permeate into the tissue biomechanics community [19, 20, 21, 22, 23, 24]. For example, we have recently tackled the propagation of material behavior uncertainty through reduced order models and Gaussian process (GP) surrogates in the context of reconstructive surgery [25, 17]. Our methodology relies on simulation of many reconstructive surgery procedures spanning a range of inputs, namely, tissue mechanical properties and flap design parameters. The Bayesian surrogate is computationally inexpensive and enables tasks such as parameter calibration, uncertainty propagation, and design optimization. Other examples of how data science is impacting biomechanics include data-driven constitutive modeling, multiscale homogenization, and Bayesian model selection [26, 27, 28, 29].
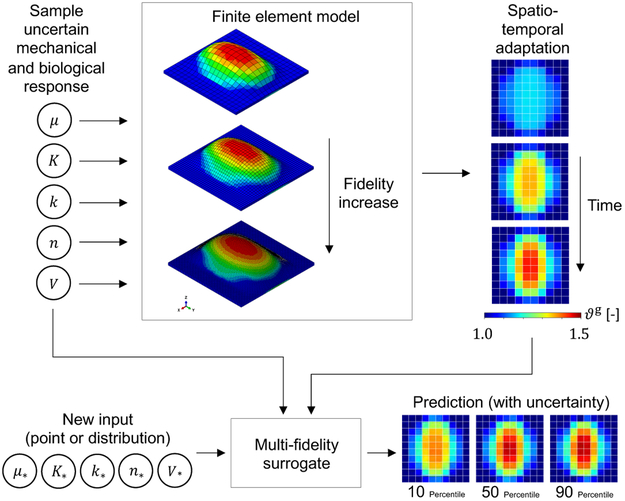
Here we present the use of Bayesian surrogates to enable uncertainty analysis of tissue growth and remodeling. We focus on tissue expansion. Unlike our previous work which dealt with uncertainty in variables that impact the state of deformation and stress at a single instant in time, the growth and remodeling process entails incorporating uncertainty in biological parameters which propagates through time coupled with the mechanical equilibrium problem (see Figures 1 and 2). In turn, the corresponding computational models are also more expensive to evaluate compared to mechanical equilibrium at a single time instant. To deal with this challenge, we propose to use multi-fidelity machine learning techniques [30]. While in this study we rely solely on simulation data, an added benefit of the multi-fidelity framework is that it enables combination of different kinds of data, including from experiments [31].
Figure 1:
Multi-fidelity surrogate for skin growth. The uncertain input space consists of the mechanical and biological response parameters as well as the volume of the expander: [μ, k, K, n, V] where μ is the shear modulus, and k, K, and n are coefficients of a Hill function controlling the growth rate. Samples of this space are used in finite element simulations with different level of detail or fidelity. The corresponding output is the growth field ϑg, which varies in space and time. The the full output is transformed into pairs of input-output data from the different fidelity models which are used to train a multi-fidelity Gaussian process surrogate. The surrogate predicts the mean and confidence interval of the growth variable over space and time at a new input [μ*, k*, K*, n*, V*].
Figure 2:
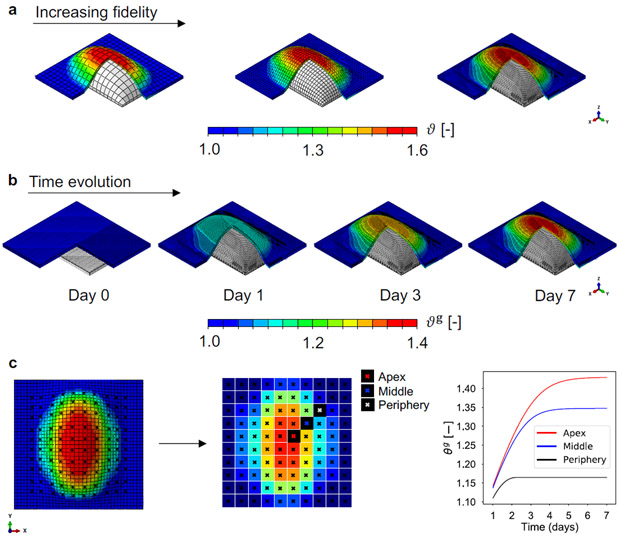
Multi-fidelity data used to construct the Bayesian surrogate of skin expansion. a) Finite element models of tissue expansion with different mesh refinement. Models are discretized with 800, 3200, and 20000 trilinear brick elements. A rectangular expander is inflated below the skin, causing total area change ϑ, characterized by greater deformation at the apex of the expander compared to the periphery. b) Time evolution of the output of interest, the growth area change ϑg, over the domain discretized with the finest mesh. The expander is inflated to either 40, 50, or 60 cc on day 1 , and the volume is held constant over 7 days. Growth increases over time, and shows spatial variation with greater growth at the apex. c) The field ϑg is defined over the entire domain, but we reduce the output to a 10 × 10 grid that we use to train the surrogate. We remark that both spatial and temporal information is used. Accordingly, the bottom right panel illustrates that for each grid point we have the time history of ϑg.
In essence, multi-fidelity approaches imply combining data with different levels of resolution or accuracy. For example, there might be some data which is very reliable, such as measurements or simulations with very detailed spatial or temporal resolution and with high accuracy. Usually, these data are difficult to obtain, either because the simulation is computationally expensive, because the parameter input space is very large, or because the experiments are costly or time consuming [32, 33]. Usually there are other, less expensive (financially and computationally) means of acquiring data, such as changing the model to a simplified one or doing experiments with less specialized equipment [34, 35]. In a multi-fidelity framework, these different sources of information are combined to create a new model that outperforms the predictions done with a single type of data [36].
The multi-fidelity approach is particularly appealing for creating predictive models of biological tissue adaptation. As mentioned previously, biological systems are characterized by inherent uncertainty in mechanical properties and biological response [37, 38, 39]. Computational models with different level of detail can be constructed to compute the growth and remodeling response over time for a wide parameter range. Here we only employ simulation data to train the surrogate, but the problem can be extended to capture our previous experimental work [3]. Furthermore, we specifically use multi-fidelity GP regression. This allows us to not only make predictions of the tissue response for a new set of inputs, but it also gives us the confidence in the prediction based on the observed data. We are hopeful that constructing this kind of data-driven model for tissue growth and remodeling will impact the clinical setting in the near future by enabling uncertainty analysis, model calibration, and treatment optimization.
Materials and Methods
Tissue growth through the multiplicative split of the deformation gradient
We start by introducing some standard notation. Let be the reference configuration and the deformed configuration of the tissue. The local deformation is captured by the gradient F = ▿Xx, whose determinant is the volume change J = det(F). For skin, since it is a membrane, we define the normal field N. This vector field, in turn, allows us to define the area deformation field induced by F, which we refer to as ϑ = ∥cof(F) · N∥.
Growth in biological materials can be done via the multiplicative split of the deformation gradient into growth and elastic components [11]
| (1) |
The growth tensor Fg captures the biological response and requires further definition of its form, which is both a constitutive and kinematic assumption. For skin, since it is a thin membrane, we consider only in plane area growth
| (2) |
where ϑg is the area growth, and Is = I − N ⊗ N is the surface identity defined in terms of the identity tensor I in and the surface normal. The split eq. (1) further implies the split of the area change into elastic and growth components
| (3) |
The elastic deformation Fe in eq. (1), encapsulates the mechanical response of the tissue. We consider skin as a hyperelastic material [40, 41]. The mechanical equilibrium of the tissue depends on the definition of a strain energy function in terms of the elastic component of the deformation only, Ψ(Fe) [42]. A thought experiment that may bring clarity to the split of the deformation gradient consists of imagining that we cut the current configuration of the tissue, , into small pieces while removing all external forces and constraints. All these small portions of material would then achieve mechanical equilibrium. Each piece is allowed to have its own equilibrium state, such that the field Fe is not necessarily the gradient of a deformation field. This is why the multiplicative split is also said to introduce an intermediate incompatible configuration [5]. The total energy released in the thought experiment depends only on the field Fe, hence Ψ(Fe). On the other hand, the equilibrium configuration of each piece of material depends on its growth history Fg. The stress in the current configuration is
| (4) |
with be = Fe·Feт. Alternatively, the stress can be expressed in the intermediate configuration or in the reference configuration, as reviewed in [43]. The overall stress field has to satisfy balance of linear momentum in the standard form
| (5) |
The simulation of the growth process with the FE method requires the derivation of the consistent tangent. We postpone the discussion of the numerical implementation until after we have introduced the corresponding constitutive equations for the biological and mechanical behavior of skin.
Constitutive modeling of growth
We already introduced the assumption that growth of skin occurs only in the plane, which is motivated by our current understanding of skin growth in tissue expansion [44, 45]. Next, we need to prescribe the evolution of the growth variable. Growth is a dynamic process and a constitutive model entails specifying the rate of change of growth in response to the mechanical cues. Following our current understanding of skin mechanobiology, we pose that the growth rate is proportional to stretch in a nonlinear fashion [7]. We depart from previous forms of the growth rate [42]. In the spirit of a systems biology approach, we assume that the elastic deformation generates a chemical signal that is interpreted by the cells, showing saturation as the input increases. Hence, we use a Hill function
| (6) |
which is parameterized by k K, ϑcr and n. In the uncertainty analysis presented here we consider the parameters k, K and n as sources of biological uncertainty. We do not consider variation in ϑcr and instead fix this parameter to 1.1. The reason for this choice is that ϑcr controls the homeostatic state. Changing this parameter would require an additional equilibration step prior to the tissue expansion procedure, which we avoid here.
Constitutive modeling of skin mechanics
Skin is a complex tissue, comprised of three layers with distinct structure and mechanical behavior in just 1 – 3 mm across the thickness [46]. The mechanical response under tension is primarily driven by the dermis, which is the intermediate layer of the skin [47]. The dermis is a connective tissue, and it is primarily made out of collagen. At moderate deformations, the stress-strain curve is only slightly nonlinear. Subjected to progressively larger strains, the skin exhibits rapid stiffening, resulting in a J-shaped stress-strain curve, characteristic of other connective tissues [48]. The collagen fiber network in the skin is a source of anisotropy [49, 50], although the fiber dispersion seen in the dermis is relatively large [51]. Extensive efforts in constitutive modeling of skin mechanics has resulted in a variety of strain energy functions[41]. In the work shown here we restrict our attention to a Neo-Hookean strain energy function
| (7) |
where I1 = be : I is the first invariant of the left Cauchy-Green elastic deformation tensor, Je = det(Fe) is the elastic volume change, μ is the shear modulus, and λ is the bulk modulus.
Like most biological materials, skin shows inherent variability in mechanical properties. For instance, it is clear to anyone that the skin varies from one anatomical region to another [52, 53]. In addition, there are changes in skin mechanics with gender, age, sun exposure, nutrition, to name a few factors [54, 55, 56]. Even individuals from similar demographics can have distinct skin mechanical behavior. With non-invasive mechanical testing through suction devices, the properties of skin under suction have been measured for a large population [57, 58]. In this paper we consider the variability in mechanical properties through the uncertainty in the parameter μ.
The stress can be calculated explicitly based on eq. (4) and eq. (7),
| (8) |
Finite element implementation
We solve the coupled problem of growth under evolving mechanical equilibrium with a user subroutine in the nonlinear FE package Abaqus (Dassault Systems, Waltham, MA). Our implementation follows closely that of [42]. We create a square domain of dimensions 10 × 10 × 0.3 cm3 and discretize it with either 800, 3200, or 20000 trilinear brick elements. As it will become clearer later on, the different mesh refinement leads to a multiple levels of fidelity in the data. A rectangular expander of dimensions 4.5 × 8 cm2 is placed underneath the skin. We use the fluid cavity feature in Abaqus. We start the simulation with the initial conditions F(t = 0) = Fe = I, ϑg (0) = 1, and an empty expander. The expander is then inflated to a given volume V by implementing a PID controller in an additional user subroutine. The degrees of freedom are the displacement vectors at the nodes, uni, and the growth field, which is discretized at the integration points . The mechanical equilibrium problem is nonlinear and has to be solved iteratively. Given a guess for the displacements uni, the deformation tensor F is available at the integration points. In the integration point subroutine the growth tensor is then updated by solving the following backward Euler problem
| (9) |
where is the growth variable from the previous converged step, is the new guess for the growth variable for the current time step t+Δt, and is the current guess for the elastic deformation component of the area change. Solving this local problem, the new Fg is constructed, which, together with the current guess for F yields Fe. The stress is calculated according to eq. (8). Finally, to drive the global Newton-Raphson iterations, we introduce the Eulerian tangent moduli
| (10) |
The elastic moduli has also an elastic and a growth component. The elastic part is
| (11) |
with , , and i the identity in the deformed configuration. The second part of the Eulerian tangent moduli is defined as
| (12) |
where , which is calculated based on the derivative of the residual eq. (9) with respect to ϑg, and n is the surface normal vector in the deformed configuration. In Abaqus, the tangent moduli used is that corresponding to the Jaumann stress rate. Thus, eq. (10) is further transformed to the desired tangent as shown in [59, 15].
Multi-fidelity Gaussian process regression
A GP is a probability measure over functions such that the function values at any set of input points have a joint Gaussian distribution [60]. This property, and the fact that for any set of observations with joint Gaussian distribution, the distribution of a subset conditioned on the rest is also Gaussian, enables making predictions at an unknown point based on previous observations. In other words, the GP regression can be interpreted in terms of Bayes’ rule as representing the posterior state of one’s knowledge about an unknown function conditional on observed data. Additionally, since the posterior is also a GP, both the expected value and covariance of any collection of new points are analytically available.
We are interested in learning a latent function f(x) from input-output observations. Assume that we have collected M observations with inputs xm in and outputs ym = f(xm)+ϵm in , where ϵm are independent identically distributed zero mean Gaussian random variables with unknown variance , to be determined. Generally, it is a good idea to include a noise term even if the measurement process noiseless, because it improves the numerical stability of the algorithm [61]. We are collectively denoting this dataset by , where is the collection of M total inputs, while y is the vector with all outputs. We posit that out prior state of knowledge about f can be described by a GP with the mean and covariance functions, m(·; θ) and k(·, ·; θ), i.e.,
| (13) |
where θ includes all hyperparameters that affect the mean and covariance functions. To keep the notation simple, assume also that even though the mean and covariance functions do not depend on it. Assuming no particular knowledge about the trend of the function, we pick a zero mean function. The choice of the covariance function models our prior beliefs about the regularity of the function (there is a one-to-one correspondence between the differentiability of the covariance function and samples from the GP probability measure [62]). Assuming that f is infinitely differentiable, we choose the squared exponential covariance function:
| (14) |
where the positive hyperparameters {ν, ℓ1, . . . , ℓd} ∈ θ model the variance of the process and the length scales of each input dimension, respectively. Note that the GP regression avoids the explicit parameterization of f and instead it let the data speak for themselves, with the only exception of these hyperparameters.
To fit the hyperparameters, we look for the θ that maximizes the log-marginal likelihood
| (15) |
where K is the M × M symmetric and positive definite matrix Kij = k(xi, xj; θ), which stores the covariance between every pair of inputs in x. As stated at the beginning of this section, the fact that any set of function values is jointly Gaussian means that the prior of the observed data together with a test pair (x*, f*) satisfy
| (16) |
where k(x*, X; θ) = (k(x*, x1; θ), ⋯ , k(x*, xM; θ))т is the cross covariance between x* and X and f* is the value of the function at the unknown input x*. Using Bayes’ rule:
| (17) |
where
| (18) |
and
| (19) |
are the predictive mean and variance, respectively.
Up to this point, the GP regression is considered for a single information source. We now extend the concept to exploit the availability of data sources of different fidelity. To be specific, different levels of mesh refinement in the FE model indicate the level of fidelity in this study, e.g., a very fine mesh corresponds to the high fidelity simulation, while a coarser mesh is associated with a lower fidelity simulation. More generally, assume that there are S levels of increasing fidelity each corresponding to an unknown function ft with t = 1, . . . , S. Even though these functions can be quite different, the assumption that they describe the same physical phenomenon makes it more likely that they exhibit similar trends. If this assumption is true, then one may learn the high fidelity function fS from a large amount of low fidelity examples and a small number of high fidelity ones. Let with t = 1, . . . , S be data sets at the fidelity levels t = 1, . . . , S. Hence, y1 represents the less accurate but inexpensive output data obtained from the lowest fidelity, while yS is the most accurate but expensive data which comes from the highest fidelity. One way to combine such multi-fidelity information is through the autoregressive approach of [63]. In this approach, one starts by assigning a GP prior on the lowest fidelity, i.e.,
| (20) |
and then modeling the next level of fidelity according to
| (21) |
for t = 2, . . . , S, where ρt−1 is a scaling factor that quantifies the correlation between output data at fidelity levels t − 1 and t, and δt (x) is a correction term with prior modeled as a GP, i.e., , with μt(·) and kt(·, ·; θ) the mean and covariance functions. Although the autoregressive approach from eq. (21) could lead to the combination of multi-fidelity information, the implementation is hindered by computational cost. The computation of the full covariance for the original autoregressive approach is unfeasible when the number of fidelity levels or the input dataset is large [63].
To overcome this barrier, the autoregressive formulation has been advanced by replacing the ft−1 prior with its posterior, denoted f*t−1. This change leads to a more numerically efficient algorithm [64]. In practical terms, the proposed switch implies that the information from different fidelity levels is decoupled and one can compute separate covariance matrices at each fidelity level recursively rather than computing the full covariance matrix for all S levels at once. The operation count to compute the inverse of the covariance by Cholesky decomposition is for each fidelity level, and the total operation count becomes , instead of that would be needed for the full covariance of all fidelity levels. We also remark that the dataset for each fidelity has nested training inputs, Xt ⊆ Xt−1, which is not necessary but enables a closed form expression for the parameters in the multi-fidelity GP regression. Finally, we note that in [64], a constant value of ρt−1 was used, which captures linear correlations between different fidelity models. Of course, ρt−1 can also be a function of the input ρt−1(x), to allow for nonlinear correlations. Recently, the authors of [31] have proposed a new approach which not only maintains the same philosophy of [64] but also captures nonlinear correlations between different levels of fidelity.
The approach of [31] is a kind of deep GP in which the GP posterior from a previous inference level is used as one more dimension in the training input dataset of next level of fidelity. Hence, the training input dataset ends up having d + 1 dimensionality for all except the lowest level of fidelity. This approach thus replaces eq. (21) with the nested model
| (22) |
where [31] . We also assume that the input data points are nested, similar to the autoregressive scheme before. A covariance function yielding function samples of the form of eq. (22), see [31], is:
| (23) |
where kρt, kft, and kδt denote covariance functions with hyperparameters θρt, θft, and θδt, respectively. Note that kft makes use of the function value at the t − 1 level of fidelity, and not the input point at the t level of fidelity. In [31], the squared exponential kernel, eq. (14), was employed, and we do the same in this paper.
Except for the lowest level of fidelity, which is a standard GP model and has a Gaussian as posterior, the posterior distribution of f*t−1(x*) with t ≥ 3 is no longer Gaussian since the GP of a GP is not a GP anymore. We use Monte Carlo integration to calculate the predictive mean and the corresponding variance of the posterior distribution, except at the lowest level of fidelity.
The multi-fidelity GP regression in eq. (22) can be applied to various applications in which it is desirable to combine information obtained with different fidelity. For example, combining data from finite element models with different degree of mesh refinement [65], linearization of nonlinear mathematical expressions [66], and reduction of model dimension such as the approximation of a 3-D physical system with a 1-D formulation [67], are a few examples in which one can get different fidelity of data for the same system of interest. In addition, experimental data might also be used as one level of fidelity. In this study, we deal only with simulation data. Three different levels of fidelity are considered, each corresponding to a different discretization scheme in the FE model (see Figure 2a). Note that the lowest fidelity level is expected to be inaccurate yet really inexpensive to evaluate (approximately 10 minutes on 1 CPU). In contrast, the highest fidelity model is much more accurate but computationally expensive (approximately 6 hours on 1 CPU).
For the GP regression in this study we used the open source library GPy [68], and the multi-fidelity GP regression code from [31].
Propagation of uncertainty in the biological and mechanical response of growing skin
As discussed in the previous section, we build multi-fidelity surrogates to predict the deformation and growth of skin resulting from tissue expansion. The tissue expansion protocol is determined by the inflation volume V, and the inflation timing, i.e. the time that the surgeon waits before the next inflation step. We do not consider uncertainty in these variables. Rather, we fix the volume to V = 40, 50, or 60 cm3 (cc), common in clinical practice [7, 4], and a time period of t = 7 days, also a common time window between consecutive inflation steps [7, 4]. We remark that in the majority of the results we show the output from three different GPs, each for a different volume. However, the volume can be considered as an input parameter for the regression, as we show towards the end of the results section. The uncertainty in the response is due to either the mechanical or the biological response of the tissue. The shear modulus μ is considered as the only source of uncertainty for the mechanical response, and the parameters k, K, n are the sources of biological uncertainty. The possible ranges for these parameters are summarized in Table 1. These ranges have been determined based on the literature[58, 57] and our previous work on a porcine model of tissue expansion [3, 7].
Table 1:
Mechanical and biological parameter ranges
| Parameter | Range |
|---|---|
| μ [MPa] | [0.10,1.00] |
| K [−] | [0.02,0.06] |
| k [−] | [0.10,1.00] |
| n [−] | [0.80,1.20] |
We note that the FE simulation leads to a deformation and a growth field over the domain. In the past we have used principal component analysis to extract the main features of the deformation and stress fields [25]. Here, we instead opt to keep the spatial analysis consistent with our animal protocol [7], and create independent surrogates for each region from a 10 × 10 grid. The outputs for the surrogates for each of these regions are the total deformation ϑ (Figure 2a) and the growth variable ϑg over time (see Figure 2b and c).
Results
Creation of GP surrogates
The input parameters for mechanical and biological response and their corresponding range are shown in Table 1. For the low fidelity data we sample 100 points from the space [μ, K, k, n] using Latin hypercube sampling (LHS), and we extend these points to a 5-dimensional input space by including time as the additional input. These input points are denoted . Likewise, we generate the input datasets and X3 by sampling additional 50 and 10 input points from [μ, K, k, n], respectively. In order to satisfy the requirement of nested input datasets, we run low fidelity simulations for all input points , the medium fidelity model is evaluated at , and the high fidelity model is only run for X3. This strategy not only satisfies nested inputs for increasing fidelity, but also preserves the LHS features of evenly and randomly distributed points over the input space. The FE models with increasing fidelity are depicted in Figure 2a. For each simulation, we inflate the expander to the volume V = 40, 50, or 60 cc at day 1 and keep the volume constant over 7 days. Note that in the majority of this section we create separate multi-fidelity GP surrogates for each volume, but we also show that the volume can be used as an additional input during regression as depicted in Figure 10. Note that the output of the simulations is the growth field ϑg over the domain and across time (see Figure 2b). As noted, time is used as an input in the regression, and the spatial variation is captured by creating surrogates independently for the 10 × 10 grid illustrated in Figure 2c.
Figure 10:
Prediction of area growth, ϑg, using GP surrogates trained using the inflation volume V as an input during the regression. With respect to temporal variation, only growth at day 7 is considered. Regarding spatial variation, growth at the three points of interest: periphery (a), middle (b), and apex (c), is shown with respect to the change of V. Uncertainty in material properties for two age groups is also considered, as described in the main text.
The simulation in Figure 2b shows the growth field over time for a single input point corresponding to the mean value of the parameter range in Table 1. Yet, even for a single input point, we note that the simulation shows the expected trends associated with skin growth in tissue expansion: the growth field is greatest at the apex of the expander and less toward the periphery, and the response is nonlinear [69].
The data from the 230 simulations are used to build the surrogates according to the Materials and Methods section.
Validation of the GP surrogates
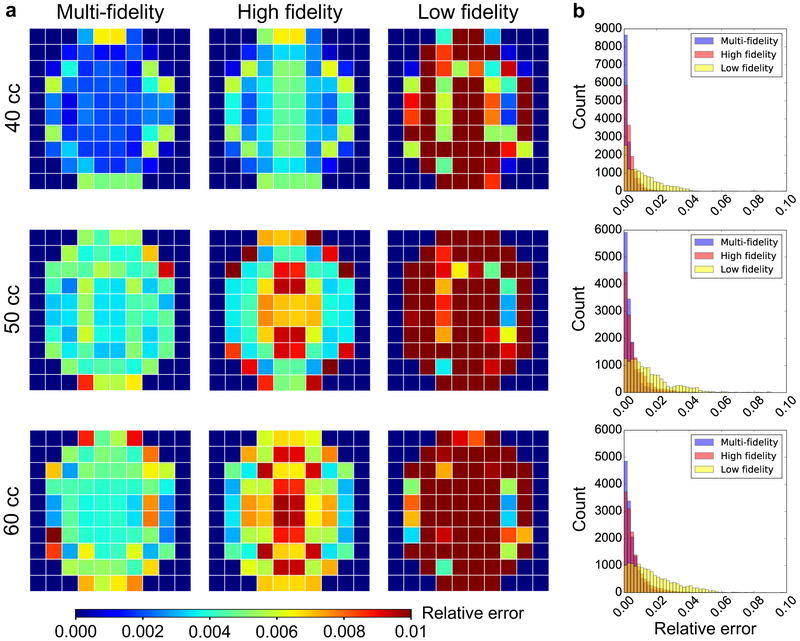
We create a validation dataset by sampling 30 additional points from the [μ, K, k, n] space using LHS. For these points we only run the highest fidelity model which we consider as the true response in this paper. Figure 3a shows the average error of the surrogates compared to the validation set for each of the 10 × 10 grid points. Each row in the figure corresponds to a different volume. In addition to showing the error in the prediction using the multi-fidelity GP regression, we also show the error for two alternative surrogates, the high fidelity GP and the low fidelity GP. As the name implies, the high fidelity surrogate is built with data from the most detailed FE model only, while the low fidelity GP uses only the results from the coarsest mesh. As desired, the multi-fidelity scheme outperforms the single fidelity surrogates. Figure 3b shows the histograms of the relative error for all the validation points (30 input parameters × 7 days × 100 locations), further illustrating the quality of the multi-fidelity GP surrogate.
Figure 3:
Validation of the surrogates against high fidelity simulations that were not used in the training. a) Average of relative error for the validation dataset composed of 30 input parameters × 7 time points for each of the 10 × 10 grid points. The multi-fidelity scheme is compared against single fidelity Gaussian process (GP) surrogates, i.e. surrogates trained with either only high or low fidelity data. The multi-fidelity GP surrogate outperforms the alternatives. b) Histograms of the error used to create the contours in a.
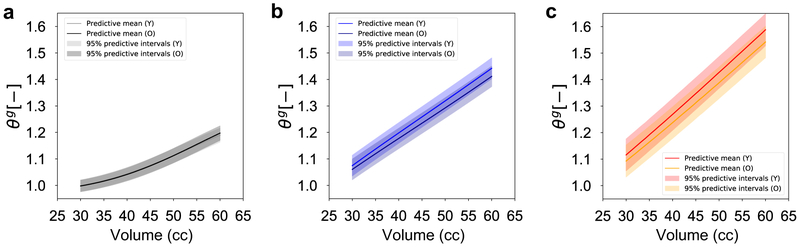
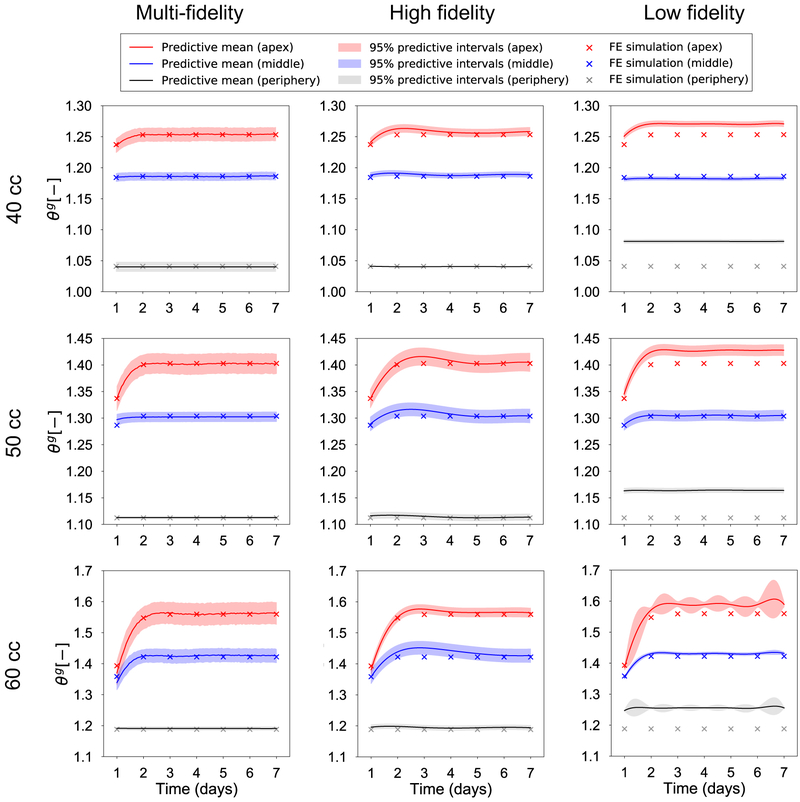
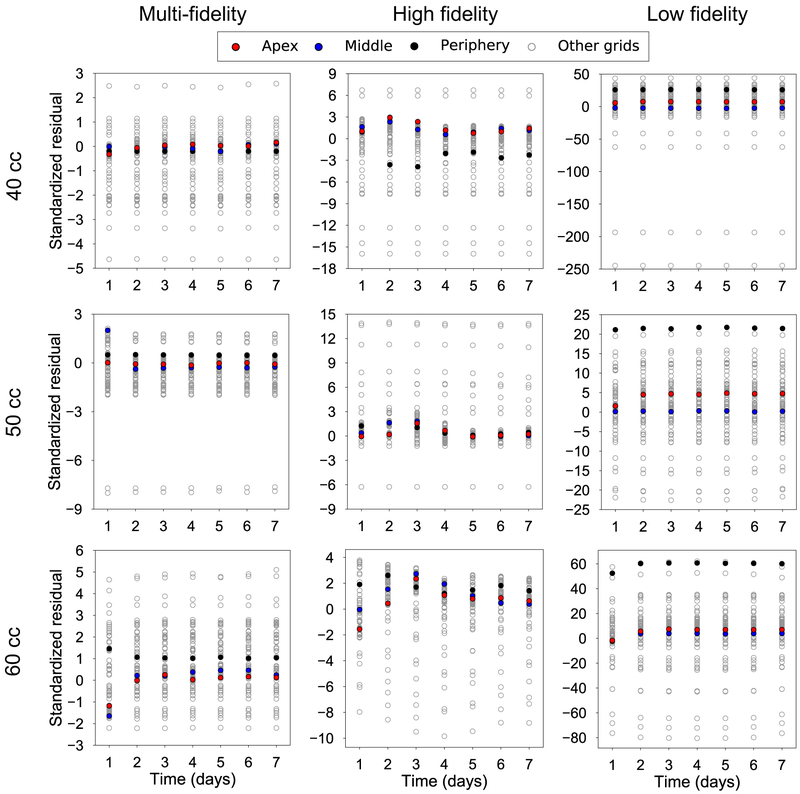
Given that the output data varies not only in space but also in time, Figure 4 focuses on the temporal variation. Once again, we are interested in the performance of the multi-fidelity scheme against single fidelity approaches. Figure 4 shows the temporal variation of ϑg for the three volumes of interest and three points of interest: the apex, a middle point, and a point at the periphery of the expanded region (see also Figure 2c). The input point for the plots in Figure 4 is the mean value of the parameter ranges in Table 1. Alongside the predictions from the surrogates, we show the results from the high fidelity simulations at the same input. Crucially, Figure 4 also shows the confidence intervals predicted by the surrogates based on the observed data. Undoubtedly, being able to show the uncertainty in the prediction is one of the main appeals of GP surrogates. To further analyze the difference between the surrogates, Figure 5 shows scatter plots of the standardized residual for the three volumes of interest and for all grid points. The standardized residual is the ratio of error between the true and the predicted values divided by the standard deviation of the prediction. If the GP surrogate is well calibrated, we expect to see the values of the standardized residual to be contained in the [−3, 3] confidence interval. Moreover, packing of the scatter plot around 0 is reflective of smaller errors in the prediction. Therefore, from Figure 5 we see that the multi-fidelity scheme shows standardized residuals well within the [−3, 3] range and mostly around 0, as desired. The principal observation from Figure 4 and 5 is that the low fidelity surrogate evidently performs poorly compared to the two other alternatives.
Figure 4:
Validation of the temporal response predicted by the surrogates against the corresponding high fidelity simulation. Plots of the growth variable ϑg are predicted for 3 points of interest: the point in apex, middle, and the periphery of the expanded area. The test input for the surrogates is the mean of the parameters in Table 1. The output of the corresponding high fidelity simulation is shown for validation. The evaluation of the Gaussian processes (GPs) results in the prediction of a mean value and the corresponding variance, a key feature of Bayesian surrogates. The low fidelity surrogate is completely inaccurate, while the multi-fidelity and high fidelity GPs have good agreement with the true response in all three volumes.
Figure 5:
Validation of the temporal response predicted by the surrogates against the corresponding high fidelity simulation. The test input is the mean of the parameters in Table 1. The standardized residuals are shown for the 100 grid points for three volumes of interest, V = 40, 50, and 60 cc. If the surrogates are trained properly, the standardized residuals should fall within the [−3, 3] confidence intervals as can be observed for the multi-fidelity GPs.
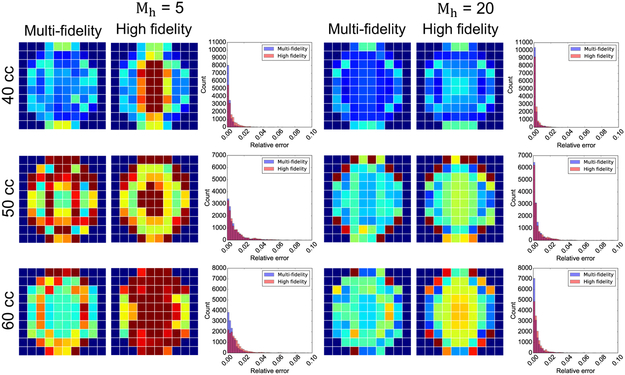
Our last validation experiment is to show the trade-off between the number of high fidelity evaluations for training and the quality of the multi-fidelity surrogate compared to the high fidelity GP. It is reasonable to expect that as the number of high fidelity training points increases, the single fidelity GP built with the high fidelity data alone might outperform the multi-fidelity approach. For the data shown in Figures 3 to 5, a total of 230 simulations were used for training, out of which Mh = 10 simulations were done with the most detailed finite element model. Figure 6 shows the results when there are either Mh = 5 or Mh = 20 high fidelity function evaluations available for training of the surrogates. With Mh = 5, both the single and multi-fidelity schemes perform poorly in terms of average relative error over the validation set, while for Mh = 20 the multi-fidelity approach continues to outperform the high fidelity GP (Figure 6). This trend is clearer when looking at the histograms of the relative error shown in Figure 6.
Figure 6:
Effect of changing the number of high fidelity function evaluations on the performance of the multi-fidelity and high fidelity GP surrogates for inflation volumes V = 40, 50, and 60 cc. Average error over the 10 × 10 grid and histograms of the error are shown for the case when there are either Mh = 5 or Mh = 20 high fidelity function evaluations available for training. For Mh = 5 both surrogates perform poorly, while for Mh = 20 the multi-fidelity GP surrogate outperforms the single fidelity approach
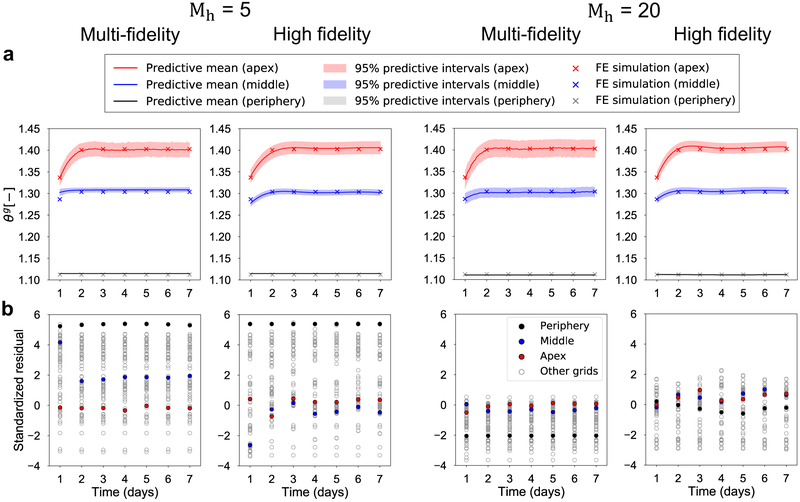
We then focus on the performance of the surrogates over the temporal domain. Figure 7 shows the validation results for V = 50 cc only. Results for other volumes are shown in the Supplementary materials. The trends are similar between the different volumes: the multi-fidelity surrogates outperform high fidelity models for both Mh = 5 and Mh = 20. More quantitative comparison is represented in Figure 7b in terms of the standardized residual for all 100 grid points for all the validation simulations. Not surprisingly, Mh = 20 leads to better performance than Mh = 5 for all volumes. Once again, the standardized residuals confirm that the multi-fidelity scheme outperforms the single fidelity schemes. However, these results also underscore the importance of choosing a suitable number of high fidelity evaluations. If there are too few high fidelity evaluations, here Mh = 5, the multi-fidelity GP surrogate itself cannot recreate an accurate GP surrogate model. On the other hand, if the number of high fidelity evaluations is high enough, Mh = 20 here, the high fidelity GP regression itself is already accurate enough and there is no more need to incorporate low fidelity information to improve the prediction.
Figure 7:
Effect of changing the number of high fidelity function evaluations on the performance of the multi-fidelity and high fidelity GPs for V = 50 cc. The test input for the surrogates is the mean of the parameters in Table 1. Results are shown for the cases in which either Mh = 5 or Mh = 20 high fidelity function evaluations are available for training. a) Prediction of the temporal evolution of the growth variable ϑg for three points of interest: apex, middle, and periphery of the expander. Plots show the predictive mean and confidence intervals alongside the truth (corresponding high-fidelity FE simulation). b) Standardized residuals for all 100 grid points and 7 time points.
Uncertainty propagation: skin material properties and biological response
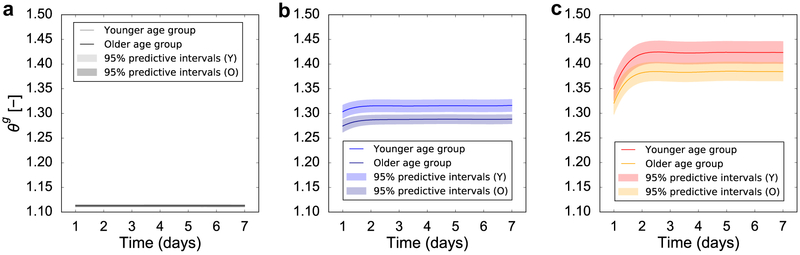
We use the validated surrogate to investigate the effect of uncertain mechanical and biological response on the resulting tissue growth. We first set the biological parameters [K, k, n] to their mean value and focus on the variation of the material parameter μ. We remark that the range for the biological parameters is based on our previous experience with the porcine model of tissue expansion [69, 7]. However, without any additional detailed knowledge about the distribution of the biological parameters, we assume the mean of the range to be a meaningful choice. For the mechanical response, on the other hand, we know that skin mechanical properties change with patient demographics. Here we focus on the effect of aging [56, 55]. Testing of skin in vivo with suction devices has enabled determination of mechanical function parameters for a wide patient population [58, 57]. In particular, in [58], the vertical displacement of skin under suction (with the same value of negative pressure used for the entire patient population) is reported as a function of age. Based on this report, we estimate that older skin (60-80 year old demographic) is 2.5 times stiffer compared to younger skin (20-40 year old demographic). From their data, it is also clear that there is some variance of mechanical properties for each age group [58]. Hence, we consider two normal distributions of μ to capture the variation in mechanical properties reported in [58]. For the younger group we assume that μ follows a normal distribution with mean μy = 0.3 and standard deviation 0.051, which results in a 95% confidential interval [0.2, 0.4] for μy. For the older individuals we consider also a normal distribution, with mean μo = 0.75 and standard deviation 0.026, resulting in [0.7, 0.8] as the 95% confidential interval of μo. We propagate this uncertainty through the surrogate. To do so, we sample 100 points from the distribution of μ for each of the age groups, and evaluate the surrogate. Then, collecting the 100 surrogate evaluations, we determine their mean and confidence interval with Monte Carlo integration [31] .
In Figure 8, we show the results for the three points of interest (apex, middle, and periphery) for V = 50 cc, while results for other volumes is available in the Supplementary materials. The younger group tissue properties lead to a higher growth, especially at the apex compared to the older group (Figure 8). The mean value of the response has similar trends in both groups, with growth reaching equilibrium by day 3. The uncertainty in the growth for the younger group is greater compared to the older group, which is expected since the uncertainty in the material properties for the younger group is much larger compared to that of the older group.
Figure 8:
Propagation of mechanical response uncertainty on the resulting tissue growth at periphery (a), middle (b), and apex (c) for V = 50 cc. We consider two age groups with different distribution for the shear modulus, μ. For the younger group, the tissue parameter is normally distributed with mean μy = 0.3 and standard deviation 0.051. For the older group, the mean is μo = 0.75 and the standard deviation is 0.026. We sample these distributions and use the surrogate to predict the resulting area growth, ϑg, at three locations of interest. The younger group shows greater growth compared to the older group at the middle (b) and apex (c) points, while the periphery (a) point shows little difference between age groups.
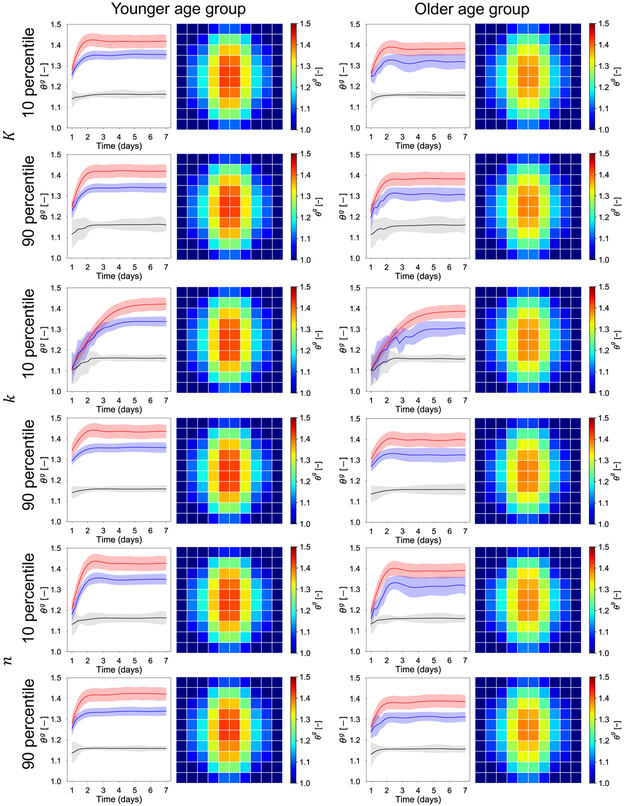
The second part of the uncertainty propagation analysis is to investigate the effect of uncertainty in the biological response. Lacking specific knowledge of how these parameters vary with different demographics, we focus on the effect of choosing these parameters to be either their 10 percentile or 90 percentile. We still consider the two age groups, but present only the results for V = 50 cc in Figure 9. For each age group, we keep two of the three biological parameters at their mean, and vary the remaining parameter. We show the transient response for the three locations of interest, as well as the contour of growth (the 50 percentile of the predicted ϑg distributions) at day 7. It is immediately clear that the response at day 7 is only mildly affected by the biological parameters. In other words, while the material response leads to a clear difference at day 7 between age groups, the effect of the biological parameters is mostly seen in the transient response. The parameter K in the Hill function describing growth is related to the saturation of the growth rate with respect to the elastic stretch. Consequently, a smaller value of this parameter leads to a greater sensitivity of the growth rate and to an apparent underdamped response. The larger the K, the greater the deformation that is needed for saturation of the growth rate, resulting in curves with greater damping. The parameter k is associated with the time scale of adaptation. A smaller value of k leads to a slower response. When k is set to the 10 percentile value, the growth extends up to day 5. Lastly, the parameter n controls the nonlinearity of the growth rate in response to applied stretch. When n is set to the 10 percentile, the response is underdamped. When n is set to the 90 percentile, the growth curves achieve equilibrium quickly and without oscillations for both age groups.
Figure 9:
The effect of biological response uncertainty coupled with the uncertainty in the mechanical behavior for the two age groups. The two age groups are differentiated by the mechanical response μ. For the young group the mean value of the shear modulus is μy = 0.3, with standard deviation 0.051. For the old group, the mean value of the shear modulus is μo = 0.75, and the standard deviation is 0.026. The contours of the growth field ϑg show distinct trends between the two age groups, but little variation as the biological parameter [K, k, n] are varied. At day 7, the young group has an average growth greater compared to the older group. The biological parameters mostly influence the transient response. The parameter K controls the saturation of the growth rate in response to elastic stretch, leading to either underdamped or overdamped curves for the three points of interest: apex (red), middle (blue) and periphery (black). The parameter k controls the speed of the adaptation. The parameter n influences the nonlinearity of the growth rate function, leading to underdamped or overdamped responses.
Effect of expansion volume on tissue growth under uncertainty
Our second analysis is to include the inflation volume V as an input dimension for regression. Therefore, the input training dataset becomes [μ, K, k, n, V] with V = 30, 40, 50, and 60 cc. For this analysis, we only use ϑg at day 7, i.e., we ignore the temporal response in this case. Nonetheless, a full regression including the evolution of ϑg over time is also possible. After we build the multi-fidelity GPs, we propagate the uncertainty in the mechanical response corresponding to the two age groups as before. The results are shown in Figure 10. Because the underlying assumption of tissue adaptation is stretch-driven growth, the value of ϑg reflects the total area stretch ϑ, which, in turn, is determined by the volume of the expander. Higher volumes lead to increasingly more stretch and consequently more growth. However, there is spatial variation, with the apex point showing the more pronounced increase in growth with increasing volume compared to the middle and periphery points. This result underscores the importance of accounting for spatial heterogeneity in designing tissue expansion protocols.
It should also be noted that the uncertainty in the mechanical properties of the tissue leads to a fairly constant variance in the prediction for different volumes. In other words, the uncertainty in the prediction of skin growth accounting for the variation in the mechanical response is not sensitive to the volume change. In fact, this observation then prompts the sensitivity analysis presented in the next subsection.
Sensitivity analysis
The last subsection of the results focuses on a global sensitivity analysis. We follow the Sobol sensitivity analysis [70] using the SALib python library [71]. The main idea of the Sobol sensitivity analysis is to decompose the variance of the model output into the contributions attributed to individual inputs. For example, an input component is fixed while the other components are varied. If the resulting variance in the predictions is large, the fixed component of the input is less influential on the output, and vice versa. After accounting for the total variance and normalization using the conditional distribution, the first-order sensitivity index can be calculated. This concept can be extended to higher order sensitivity indices that take into account correlations between different components of the input, e.g., the second-order sensitivity index measures the contribution of pairs of input components. When the dimension of the input, d, increases, the correlation between input components increases as 2d − 1. The total-order sensitivity index for one specific component of the input can be deduced in a reverse manner, i.e., the expectation of the variance of the model output is calculated when the set of evaluation points does not have any correlation with the component of interest [72].
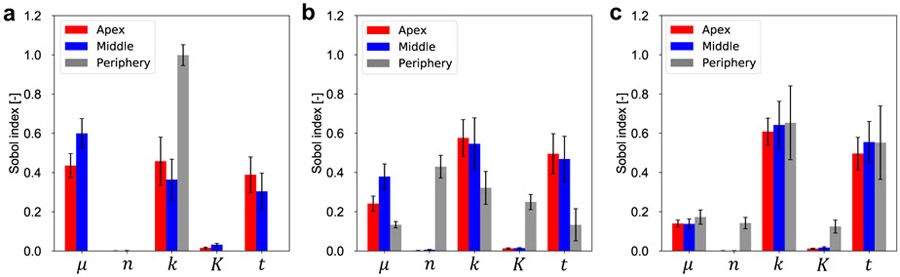
We generate a total of 12,000 evaluations of the surrogate, decided from N × (2d + 2), where N = 1,000 is the number of samples, and d = 5 is the dimension of the input space. We use Saltelli’s sampling scheme [73]. The output dataset is retrieved, and then processed to get the total-order sensitivity index for the apex, middle, and periphery spatial locations of interest, and for three different volumes (Figure 11). We remark that the calculation of the Sobol indices was done via Monte Carlo integration. Therefore, the values reported in Figure 11 are bound to have some noise. Accordingly, we report the uncertainty in the indices. Because each panel (Figure 11a to c) is derived independently, it should be interpreted individually even though the volume change could also be treated as an input. In fact, it should be noted that the volume consistently influences the variance of the output.
Figure 11:
Sobol sensitivity analysis of area growth, ϑg, with respect to individual input dataset, [μ, n, k, K, t], for volumes V = 40 (a), 50 (b), and 60 cc (c). Here, t indicates day as time. In each panel, three points of interest are considered. Each bar indicates the total-order index. The associated 95% confidential intervals are also shown.
For the apex and middle points, n and K in the Hill function have less impact on ϑg for all three volumes. In contrast, μ, k, and time are influential on ϑg, but their importance changes for the different volumes. As volume increases, the mechanical parameter, μ, has less contribution than k and time. This result follows from the spatial distribution of the strains, and from the fact that ϑcr = 1.1. As a consequence, for small volumes, the lower area changes, close to ϑcr, coupled with the spatial distribution of the strain field plays an important role to determine the amount of growth. As the volume increases, the strains become more homogeneous independently of μ, and they are always larger than the critical value. Therefore, k and t become more important than μ. These trends are particularly consistent for the middle and apex points. For the periphery point, however, the stretch is always close to the critical value. In the 40 cc case (Figure 11a), the stretch in the periphery rarely exceeds ϑcr, and the growth is negligible at this location for the lowest volume. As the volume increases, the periphery point also shows similar trends compared with the apex and middle points.
Discussion
In this manuscript we develop a multi-fidelity GP regression surrogate to investigate the effect of uncertain mechanical and biological response of soft tissues on the resulting spatio-temporal growth field. We focus on tissue expansion, but the analysis shown here could be used to study uncertainty in growth and remodeling for other tissues in clinically relevant scenarios [39, 74]. The main motivation for our analysis is the inherent variability in living tissue, both in terms of mechanical properties and also adaptation to environmental cues [75]. While computational models of growth and remodeling have furthered our understanding of tissue mechanobiology, the role of uncertain parameters in these models remains poorly studied [8]. Machine learning techniques are needed to enable uncertainty analysis of biological systems due to the high computational cost of detailed models, which prevents more traditional analysis such as Monte Carlo sampling [76]. We have shown before that GP surrogates enable uncertainty analysis of stress contours in reconstructive surgery applications [7, 17]. Unfortunately, as the complexity and computational cost of the model increases, for example going from a static equilibrium analysis to a model of skin growth in tissue expansion, standard GP regression becomes unattainable. The multi-fidelity strategy used here circumvents this limitation. Instead of relying on a single, very detailed model, we create three models with increasing refinement and use data from all three models to train the surrogate.
Our results confirm that the multi-fidelity GP regression surrogate outperforms the single fidelity GPs over the validation set. Interestingly, the low fidelity information is valuable even if the corresponding surrogate shows that the low fidelity model is not an accurate representation of the system. Yet, since all models have correlated trends in the growth field, the low fidelity information can supplement the limited number of high fidelity simulations in the multi-fidelity approach [31]. In contrast, the epistemic error, which results from the limited number of training, cannot be reduced in the high fidelity GP, as evidenced in Figure 3 and 4, and in the scatter plots of the standardized residuals in Figure 5.
Design of the training dataset for the multi-fidelity surrogate is a key consideration in the methodology. Evidently, the cost of training the multi-fidelity GP regression depends strongly on the number of high fidelity function evaluations. Too few and the multi-fidelity model will be spoiled by the inaccurate low fidelity data. Similarly, too many high fidelity simulations defeat the purpose of the multi-fidelity scheme. We tested different numbers of high fidelity function evaluations but did find a clear threshold for choosing this number. Our results indicate that the smallest number of high fidelity function evaluations, Mh = 5, led to poor performance of the surrogates, whereas either 10 or 20 high fidelity simulations paired with one order of magnitude more medium and low fidelity simulations led to an accurate surrogate. This trade-off largely depends on the sensitivity of the system to the input parameters. The results in Figure 6 and 7 together with the uncertainty propagation analysis indicate that, for the constitutive models we chose and for the range of parameters considered, only a few high fidelity simulations are required. Further work is needed to establish design parameters for the training set of the multi-fidelity surrogates.
As mentioned at the beginning of this section, a key feature of biological tissue that has been often disregarded in the field of tissue mechanobiology is uncertainty in the mechanical and biological response. Moreover, the high nonlinearity of the growth process is one of the main difficulties to accurately investigate correlation of the growth and remodeling fields with varying mechanical and biological parameters. Our study is precisely tailored to tackle this challenge. In turn, this capability is crucial to enable the deployment of computational models of growth and remodeling in relevant clinical settings. For instance, tissue expansion protocols are used for a wide array of patient demographics, from children with large congenital defects [4], to burn wounds in adults [77], breast reconstruction after mastectomy [78], and melanoma surgery in older adults 79]. These different patient populations have distinct skin mechanical properties [56, 53, 58, 57]. In turn, computational models of skin expansion have to account for this kind of variability to guide decision making and treatment planning. Here we focused on the effect of age on the stiffness of skin based on the evidence from the literature. As shown in Figure 8, we are able to make predictions of the resulting growth probability distributions when the mechanical properties of the tissue follow realistic normal distributions that vary with age. A key insight from the analysis is that skin from younger adults is expected to grow more under the same tissue expansion protocol based solely on its mechanical properties, but the uncertainty of this result is larger compared to the older adult population.
Continuing with the two different groups in terms of the mechanical response, we further tested the sensitivity of the growth response to the biological parameters. The main insight from this investigation is that, for the specific form of the growth law and the range of parameters considered, the variation in the biological parameters affects the transient response, within the first 5 days post-inflation, but has little effect on the growth contours at day 7 (Figure 9). This kind of knowledge can help design safer inflation protocols. A more thorough calibration of the model is of course needed, but our current analysis suggests that waiting 7 days between expansions may be a good decision to ensure that the skin has reached a stable point before the next inflation. As mentioned in the introduction, weekly expansions are indeed common [4], but more aggressive expansion protocols have also been proposed [80].
Our work is not free of limitations. Regarding the construction of the surrogate, we rely on simulation data alone and assume that these data are noiseless [63, 31]. As discussed in [31], introducing noise into the training data set is more representative of the real system, especially if we are to extend our framework to include experimental data. Another limitation of our methodology is that the design of the training data set remains arbitrary and it is thus difficult to anticipate the number of function evaluations needed to train an accurate surrogate. Further work in this area is particularly important since one would like to avoid unnecessary evaluations of the high fidelity model. Thirdly, here we focus on a single inflation step and on a single expander shape, our future work will extend the analysis to different expander shapes and inflation protocols. We will also continue to integrate the computational model with our experimental model of tissue expansion [7]. Lastly, here we used a simple isotropic material model, the Neo-Hookean strain energy, to model skin. In reality, skin is an anisotropic material [51, 49]. We have shown in previous simulations that anisotropic material properties lead to anisotropic growth fields [43]. We have also observed this experimentally [3]. Therefore, our future work will also include the effect of anisotropy on growth and remodeling of soft tissues.
Conclusions
We present a multi-fidelity GP surrogate to predict the growth of skin in tissue expansion when the mechanical response and the biological response are assumed uncertain. The multi-fidelity GP surrogate outperforms single fidelity approaches, making it particularly appealing for uncertainty analysis of biological systems, which are highly nonlinear and for which high-fidelity FE models are computationally expensive. We expect that the results shown here will be valuable beyond their application to tissue expansion, for the analysis of other soft tissues that growth and remodel in relevant clinical scenarios.
Supplementary Material
Highlights.
We create a multi-fidelity GP surrogate to predict skin growth in tissue expansion and investigate the effect of uncertain mechanical and biological model inputs on the resulting trends of the spatio-temporal growth field
The multi-fidelity GP is constructed by running finite element simulations with different levels of refinement, is computationally efficient, and outperforms single-fidelity approaches
Skin from younger adults is predicted to grow more than skin from older adults for the same expansion protocol
Acknowledgements
This work was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institute of Health under award R01AR074525.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].Göktepe S, Abilez OJ, Parker KK, Kuhl E, A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis, Journal of theoretical biology 265 (2010) 433–442. [DOI] [PubMed] [Google Scholar]
- [2].Göktepe S, Abilez OJ, Kuhl E, A generic approach towards finite growth with examples of athlete’s heart, cardiac dilation, and cardiac wall thickening, Journal of the Mechanics and Physics of Solids 58 (2010) 1661–1680. [Google Scholar]
- [3].Tepole AB, Gart M, Purnell CA, Gosain AK, Kuhl E, Multi-view stereo analysis reveals anisotropy of prestrain, deformation, and growth in living skin, Biomechanics and modeling in mechanobiology 14 (2015) 1007–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gosain AK, Zochowski CG, Cortes W, Refinements of tissue expansion for pediatric forehead reconstruction: a 13-year experience, Plastic and reconstructive surgery 124 (2009) 1559–1570. [DOI] [PubMed] [Google Scholar]
- [5].Tepole AB, Gart M, Purnell CA, Gosain AK, Kuhl E, The incompatibility of living systems: characterizing growth-induced incompatibilities in expanded skin, Annals of biomedical engineering 44 (2016) 1734–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Rivera R, LoGiudice J, Gosain AK, Tissue expansion in pediatric patients, Clinics in plastic surgery 32 (2005) 35–44. [DOI] [PubMed] [Google Scholar]
- [7].Lee T, Vaca EE, Ledwon JK, Bae H, Topczewska JM, Turin SY, Kuhl E, Gosain AK, Tepole AB, Improving tissue expansion protocols through computational modeling, Journal of the mechanical behavior of biomedical materials 82 (2018) 224–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Eskandari M, Kuhl E, Systems biology and mechanics of growth, Wiley Interdisciplinary Reviews: Systems Biology and Medicine 7 (2015) 401–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Ambrosi D, Ateshian GA, Arruda EM, Cowin S, Dumais J, Goriely A, Holzapfel GA, Humphrey JD, Kemkemer R, Kuhl E, et al. , Perspectives on biological growth and remodeling, Journal of the Mechanics and Physics of Solids 59 (2011) 863–883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Taber LA, Biomechanics of growth, remodeling, and morphogenesis, Applied mechanics reviews 48 (1995) 487–545. [Google Scholar]
- [11].Rodriguez EK, Hoger A, McCulloch AD, Stress-dependent finite growth in soft elastic tissues, Journal of biomechanics 27 (1994) 455–467. [DOI] [PubMed] [Google Scholar]
- [12].Lee L, Kassab G, Guccione J, Mathematical modeling of cardiac growth and remodeling, Wiley Interdisciplinary Reviews: Systems Biology and Medicine 8 (2016) 211–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Oomen PJ, Holland MA, Bouten CV, Kuhl E, Loerakker S, Growth and remodeling play opposing roles during postnatal human heart valve development, Scientific reports 8 (2018) 1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Holland M, Budday S, Goriely A, Kuhl E, Symmetry breaking in wrinkling patterns: Gyri are universally thicker than sulci, Physical review letters 121 (2018) 228002. [DOI] [PubMed] [Google Scholar]
- [15].Rausch MK, Kuhl E, On the mechanics of growing thin biological membranes, Journal of the Mechanics and Physics of Solids 63 (2014) 128–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Alastrue V, Martinez M, Doblare M, Modelling adaptative volumetric finite growth in patient-specific residually stressed arteries, Journal of biomechanics 41 (2008) 1773–1781. [DOI] [PubMed] [Google Scholar]
- [17].Lee T, Gosain AK, Bilionis I, Tepole AB, Predicting the effect of aging and defect size on the stress profiles of skin from advancement, rotation and transposition flap surgeries, Journal of the Mechanics and Physics of Solids 125 (2019) 572–590. [Google Scholar]
- [18].Klepach D, Lee LC, Wenk JF, Ratcliffe MB, Zohdi TI, Navia JL, Kassab GS, Kuhl E, Guccione JM, Growth and remodeling of the left ventricle: a case study of myocardial infarction and surgical ventricular restoration, Mechanics research communications 42 (2012) 134–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Chabiniok R, Wang VY, Hadjicharalambous M, Asner L, Lee J, Sermesant M, Kuhl E, Young AA, Moireau P, Nash MP, et al. , Multiphysics and multiscale modelling, data–model fusion and integration of organ physiology in the clinic: ventricular cardiac mechanics, Interface focus 6 (2016) 20150083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Latorre M, Montáns FJ, Experimental data reduction for hyperelasticity, Computers & Structures (2018). [Google Scholar]
- [21].Costabal FS, Matsuno K, Yao J, Perdikaris P, Kuhl E, Machine learning in drug development: Characterizing the effect of 30 drugs on the qt interval using gaussian process regression, sensitivity analysis, and uncertainty quantification, Computer Methods in Applied Mechanics and Engineering 348 (2019) 313–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Madireddy S, Sista B, Vemaganti K, A bayesian approach to selecting hyperelastic constitutive models of soft tissue, Computer Methods in Applied Mechanics and Engineering 291 (2015) 102–122. [Google Scholar]
- [23].Costabal FS, Choy J, Sack KL, Guccione JM, Kassab G, Kuhl E, Multiscale characterization of heart failure, Acta biomaterialia 86 (2019) 66–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Peirlinck M, Costabal FS, Sack K, Choy J, Kassab G, Guccione J, De Beule M, Segers P, Kuhl E, Using machine learning to characterize heart failure across the scales, Biomechanics and modeling in mechanobiology (2019) 1–15. [DOI] [PubMed] [Google Scholar]
- [25].Lee T, Turin SY, Gosain AK, Bilionis I, Tepole AB, Propagation of material behavior uncertainty in a nonlinear finite element model of reconstructive surgery, Biomechanics and modeling in mechanobiology 17 (2018) 1857–1873. [DOI] [PubMed] [Google Scholar]
- [26].Cantwell CD, Mohamied Y, Tzortzis KN, Garasto S, Houston C, Chowdhury RA, Ng FS, Bharath AA, Peters NS, Rethinking multiscale cardiac electrophysiology with machine learning and predictive modelling, Computers in biology and medicine 104 (2019) 339–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Mihai LA, Woolley TE, Goriely A, Stochastic isotropic hyperelastic materials: constitutive calibration and model selection, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 474 (2018) 20170858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Kouchmeshky B, Zabaras N, Microstructure model reduction and uncertainty quantification in multiscale deformation processes, Computational Materials Science 48 (2010) 213–227. [Google Scholar]
- [29].Le B, Yvonnet J, He Q-C, Computational homogenization of nonlinear elastic materials using neural networks, International Journal for Numerical Methods in Engineering 104 (2015) 1061–1084. [Google Scholar]
- [30].Parussini L, Venturi D, Perdikaris P, Karniadakis GE, Multi-fidelity gaussian process regression for prediction of random fields, Journal of Computational Physics 336 (2017) 36–50. [Google Scholar]
- [31].Perdikaris P, Raissi M, Damianou A, Lawrence N, Karniadakis GE, Nonlinear information fusion algorithms for data-efficient multi-fidelity modelling, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 473 (2017) 20160751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Sahli Costabal F, Yao J, Kuhl E, Predicting drug-induced arrhythmias by multiscale modeling, International journal for numerical methods in biomedical engineering 34 (2018) e2964. [DOI] [PubMed] [Google Scholar]
- [33].Perdikaris P, Karniadakis GE, Model inversion via multi-fidelity bayesian optimization: a new paradigm for parameter estimation in haemodynamics, and beyond, Journal of The Royal Society Interface 13 (2016)20151107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nguyen N-V, Choi S-M, Kim W-S, Lee J-W, Kim S, Neufeld D, Byun Y-H, Multidisciplinary unmanned combat air vehicle system design using multi-fidelity model, Aerospace Science and Technology 26 (2013) 200–210. [Google Scholar]
- [35].Witzenburg CM, Holmes JW, Predicting the time course of ventricular dilation and thickening using a rapid compartmental model, Journal of cardiovascular translational research 11 (2018) 109–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Peherstorfer B, Willcox K, Gunzburger M, Survey of multifidelity methods in uncertainty propagation, inference, and optimization, SIAM Review 60 (2018) 550–591. [Google Scholar]
- [37].Madireddy S, Sista B, Vemaganti K, Bayesian calibration of hyperelastic constitutive models of soft tissue, Journal of the mechanical behavior of biomedical materials 59 (2016) 108–127. [DOI] [PubMed] [Google Scholar]
- [38].Sankaran S, Marsden AL, A stochastic collocation method for uncertainty quantification and propagation in cardiovascular simulations, Journal of biomechanical engineering 133 (2011) 031001. [DOI] [PubMed] [Google Scholar]
- [39].Witzenburg CM, Holmes JW, A comparison of phenomenologic growth laws for myocardial hypertrophy, Journal of Elasticity 129 (2017) 257–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Groves RB, Coulman SA, Birchall JC, Evans SL, An anisotropic, hyperelastic model for skin: experimental measurements, finite element modelling and identification of parameters for human and murine skin, Journal of the mechanical behavior of biomedical materials 18 (2013) 167–180. [DOI] [PubMed] [Google Scholar]
- [41].Limbert G, Mathematical and computational modelling of skin biophysics: a review, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 473 (2017) 20170257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Zöllner AM, Holland MA, Honda KS, Gosain AK, Kuhl E, Growth on demand: reviewing the mechanobiology of stretched skin, Journal of the mechanical behavior of biomedical materials 28 (2013) 495–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Tepole AB, Gosain AK, Kuhl E, Stretching skin: The physiological limit and beyond, International journal of non-linear mechanics 47 (2012) 938–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Purnell CA, Gart MS, Buganza-Tepole A, Tomaszewski JP, Topczewska JM, Kuhl E, Gosain AK, Determining the differential effects of stretch and growth in tissue-expanded skin: Combining isogeometric analysis and continuum mechanics in a porcine model, Dermatologic surgery: official publication for American Society for Dermatologic Surgery [et al. ] 44 (2018) 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Silver FH, Siperko LM, Seehra GP, Mechanobiology of force transduction in dermal tissue, Skin Research and Technology 9 (2003) 3–23. [DOI] [PubMed] [Google Scholar]
- [46].Benítez JM, Montáns FJ, The mechanical behavior of skin: Structures and models for the finite element analysis, Computers & Structures 190 (2017) 75–107. [Google Scholar]
- [47].Jor JW, Parker MD, Taberner AJ, Nash MP, Nielsen PM, Computational and experimental characterization of skin mechanics: identifying current challenges and future directions, Wiley Interdisciplinary Reviews: Systems Biology and Medicine 5 (2013) 539–556. [DOI] [PubMed] [Google Scholar]
- [48].Jor JW, Nash MP, Nielsen PM, Hunter PJ, Estimating material parameters of a structurally based constitutive relation for skin mechanics, Biomechanics and modeling in mechanobiology 10 (2011) 767–778. [DOI] [PubMed] [Google Scholar]
- [49].Annaidh AN, Bruyère K, Destrade M, Gilchrist MD, Otténio M, Characterization of the anisotropic mechanical properties of excised human skin, Journal of the mechanical behavior of biomedical materials 5 (2012) 139–148. [DOI] [PubMed] [Google Scholar]
- [50].Laiacona D, Cohen J, Coulon K, Lipsky ZW, Maiorana C, Boltyanskiy R, Dufresne ER, German GK, Non-invasive in vivo quantification of human skin tension lines, Acta biomaterialia 88 (2019) 141–148. [DOI] [PubMed] [Google Scholar]
- [51].Annaidh AN, Bruyere K, Destrade MD, Gilchrist MD, Maurini C, Otténio M, Saccomandi G, Automated estimation of collagen fibre dispersion in the dermis and its contribution to the anisotropic behaviour of skin, Annals of biomedical engineering 40 (2012) 1666–1678. [DOI] [PubMed] [Google Scholar]
- [52].Tonge TK, Atlan LS, Voo LM, Nguyen TD, Full-field bulge test for planar anisotropic tissues: Part i–experimental methods applied to human skin tissue, Acta biomaterialia 9 (2013) 5913–5925. [DOI] [PubMed] [Google Scholar]
- [53].Pensalfini M, Weickenmeier J, Rominger M, Santoprete R, Distler O, Mazza E, Location-specific mechanical response and morphology of facial soft tissues, Journal of the mechanical behavior of biomedical materials 78 (2018) 108–115. [DOI] [PubMed] [Google Scholar]
- [54].Daly CH, Odland GF, Age-related changes in the mechanical properties of human skin, Journal of Investigative Dermatology 73 (1979) 84–87. [DOI] [PubMed] [Google Scholar]
- [55].Limbert G, Masen MA, Pond D, Graham HK, Sherratt MJ, Jobanputra R, McBride A, Biotribology of the ageing skinwhy we should care, Biotribology (2019). [Google Scholar]
- [56].Ryu HS, Joo YH, Kim SO, Park KC, Youn SW, Influence of age and regional differences on skin elasticity as measured by the cutometer®, Skin Research and Technology 14 (2008) 354–358. [DOI] [PubMed] [Google Scholar]
- [57].Luebberding S, Krueger N, Kerscher M, Mechanical properties of human skin in vivo: a comparative evaluation in 300 men and women, Skin Research and Technology 20 (2014) 127–135. [DOI] [PubMed] [Google Scholar]
- [58].Krueger N, Luebberding S, Oltmer M, Streker M, Kerscher M, Age-related changes in skin mechanical properties: a quantitative evaluation of 120 female subjects, Skin research and technology 17 (2011) 141–148. [DOI] [PubMed] [Google Scholar]
- [59].Prot V, Skallerud B, Holzapfel G, Transversely isotropic membrane shells with application to mitral valve mechanics. constitutive modelling and finite element implementation, International journal for numerical methods in engineering 71 (2007) 987–1008. [Google Scholar]
- [60].Bishop CM, Pattern recognition and machine learning, springer, 2006. [Google Scholar]
- [61].Gramacy R, Lee H, Cases for the nugget in modelling computer experiments, Statistics and Computing 22 (2010). [Google Scholar]
- [62].Adler RJ, The geometry of random fields, SIAM, 2010. [Google Scholar]
- [63].Kennedy MC, O’Hagan A, Predicting the output from a complex computer code when fast approximations are available, Biometrika 87 (2000) 1–13. [Google Scholar]
- [64].Le Gratiet L, Garnier J, Recursive co-kriging model for design of computer experiments with multiple levels of fidelity, International Journal for Uncertainty Quantification 4 (2014). [Google Scholar]
- [65].Koziel S, Leifsson L, Multi-level cfd-based airfoil shape optimization with automated low-fidelity model selection, Procedia Computer Science 18 (2013) 889–898. [Google Scholar]
- [66].Hutchison M, Unger E, Mason W, Grossman B, Haftka R, Variable-complexity aerodynamic optimization of a high-speed civil transport wing, Journal of Aircraft 31 (1994) 110–116. [Google Scholar]
- [67].Turner MG, Reed JA, Ryder R, Veres JP, Multi-fidelity simulation of a turbofan engine with results zoomed into mini-maps for a zero-d cycle simulation, in: ASME Turbo Expo 2004: Power for Land, Sea, and Air, American Society of Mechanical Engineers, pp. 219–230. [Google Scholar]
- [68].GPy, GPy: A gaussian process framework in python, http://github.com/SheffieldML/GPy, since 2012.
- [69].Tepole AB, Gart M, Gosain AK, Kuhl E, Characterization of living skin using multi-view stereo and isogeometric analysis, Acta biomaterialia 10 (2014) 4822–4831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Sobol IM, Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates, Mathematics and computers in simulation 55 (2001)271–280. [Google Scholar]
- [71].Herman JD, Usher W, Salib: An open-source python library for sensitivity analysis., J. Open Source Software 2 (2017) 97. [Google Scholar]
- [72].Homma T, Saltelli A, Importance measures in global sensitivity analysis of nonlinear models, Reliability Engineering & System Safety 52 (1996) 1–17. [Google Scholar]
- [73].Saltelli A, Making best use of model evaluations to compute sensitivity indices, Computer physics communications 145 (2002) 280–297. [Google Scholar]
- [74].Eskandari M, Kuschner WG, Kuhl E, Patient-specific airway wall remodeling in chronic lung disease, Annals of biomedical engineering 43 (2015) 2538–2551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Sankaran S, Humphrey JD, Marsden AL, An efficient framework for optimization and parameter sensitivity analysis in arterial growth and remodeling computations, Computer methods in applied mechanics and engineering 256 (2013) 200–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Janssen H, Monte-carlo based uncertainty analysis: Sampling efficiency and sampling convergence, Reliability Engineering & System Safety 109 (2013) 123–132. [Google Scholar]
- [77].Bozkurt A, Groger A, Odey D, Vogeler F, Piatkowski A, Fuchs PC, Pallua N, Retrospective analysis of tissue expansion in reconstructive burn surgery: evaluation of complication rates, Burns 34 (2008) 1113–1118. [DOI] [PubMed] [Google Scholar]
- [78].Radovan C, Breast reconstruction after mastectomy using the temporary expander., Plastic and Reconstructive Surgery 69 (1982) 195–208. [DOI] [PubMed] [Google Scholar]
- [79].van Aalst JA, McCurry T, Wagner J, Reconstructive considerations in the surgical management of melanoma, Surgical Clinics 83 (2003) 187–230. [DOI] [PubMed] [Google Scholar]
- [80].Zeng Y.-j., Xu C.-q., Yang J, Sun G.-c., Xu X.-h., Biomechanical comparison between conventional and rapid expansion of skin, British journal of plastic surgery 56 (2003) 660–666. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.