Linear and nonlinear mechanical responses can be quite different in models for biological tissues

Abstract

The fluidity of biological tissues – whether cells can change neighbors and rearrange – is important for their function. In traditional materials, researchers have used linear response functions, such as the shear modulus, to accurately predict whether a material will behave as a fluid. Similarly, in disordered 2D vertex models for confluent biological tissues, the shear modulus becomes zero precisely when the cells can change neighbors and the tissue fluidizes, at a critical value of control parameter $s_0^{*}=3.81$. However, the ordered ground states of 2D vertex models become linearly unstable at a lower value of control parameter (3.72) [1, 2], suggesting that there may be a decoupling between linear and nonlinear response. We demonstrate that the linear response does not correctly predict the nonlinear behavior in these systems: when the control parameter is between 3.72 and 3.81, cells cannot freely change neighbors even though the shear modulus is zero. These results highlight that the linear response of vertex models should not be expected to generically predict their rheology. We develop a simple geometric ansatz that correctly predicts the nonlinear response, which may serve as a framework for making nonlinear predictions in other vertex-like models.

INTRODUCTION

The rheological properties of a biological tissue – how a tissue responds to stresses and strains – and the regulation of such properties are crucial for many biological processes. For example, mature skin tissue typically behaves like an elastic material, where cells maintain their neighbors and the tissue returns to its original shape after being stretched, just like a solid. However, in processes like wound healing, individual cells can change neighbors and migrate over long distances[3, 4] just as in a fluid. Tissues that transition between solid and fluid states have recently been shown to play an important role in development [5] and disease [6]. Thus, we would like to understand how the emergent material properties, such as the rheology, of the tissue are determined and regulated.

In traditional materials, the rheology of a material is usually characterized by a linear response variable, such as the shear modulus that describes how the mechanical stress in the material changes in response to a very small strain. More recently, it has been recognized that some biological materials behave very differently when they experience large strains instead of small strains. For example, extracellular matrix stiffens by several orders of magnitude when strained past a critical threshold [7]. In addition, it has recently been shown that models for heterogeneous confluent epithelial layers, with two cell types and an interfacial tension between them, has non-analytic cusps in the potential energy landscape so that the linear and nonlinear response are completely decoupled [8]. Both of these observations suggest that we should not necessary expect the linear response of a biological tissue to predict its nonlinear response.

Biologists and biomedical engineers are often interested in processes that involve very large strains, such as convergent extension to elongate the body of a developing embryo, or cells moving over tens or hundreds of cell diameters to close a wound. Therefore, it is important to understand whether the standard tools of linear response are valid in these systems, and if not, develop new approaches to predict the nonlinear response.

To explore this question further, we focus on homogeneous confluent epithelial monolayers composed of a single cell type. Vertex models represent these tissues as a 2D network of edges and vertices, and associate a mechanical energy with the shape of each individual cell in a tessellation. Such simple models have been surprisingly successful at describing the statistics and behavior of many biological tissues [1, 9–12]. The mechanical energy associated with cell shape is based on experimental observations in cell doublets and triplets: cells with more cadherin-based adhesion tend to share longer joint interfaces, while those with higher cortical tension tend to have smaller shared interfaces [13, 14]. In all of this work, an important control parameter of the model is the dimensionless cell shape index s₀, which is the ratio between the cell’s cross-sectional perimeter and the square root of the cell’s cross-sectional area.

The next step is to understand how cell shapes influence the large-scale rheological properties. Within the framework of vertex models, Farhadifar et al. [1] and Staple et al. [2] performed a beautiful and comprehensive investigation of the linear response of ordered tessellations, which are the ground states of the vertex model. They demonstrated that the shear modulus of ordered ground states of the 2D vertex model disappear for all shapes with s₀ > 3.722 = s_hex, the perimeter to area ratio of a regular hexagon. In other words, the energy landscape is flat with respect to small perturbations for s₀ > 3.722. However, these works did not investigate the nonlinear response – how cells rearrange and change neighbors at larger strains.

In a confluent tissue with no cellular proliferation or death, the only way for a cell to change neighbors and diffuse over large distances is to make a series of topological rearrangements, or T1 transitions. During this process, an edge between two cell shrinks to zero length and then a new edge grows between two new cells, as illustrated in Fig. 1(a–c). Many such exchanges lead to cell diffusion. Therefore, an important parameter that controls the nonlinear response of the tissue is the height of the mechanical energy barrier associated with a T1 transition.

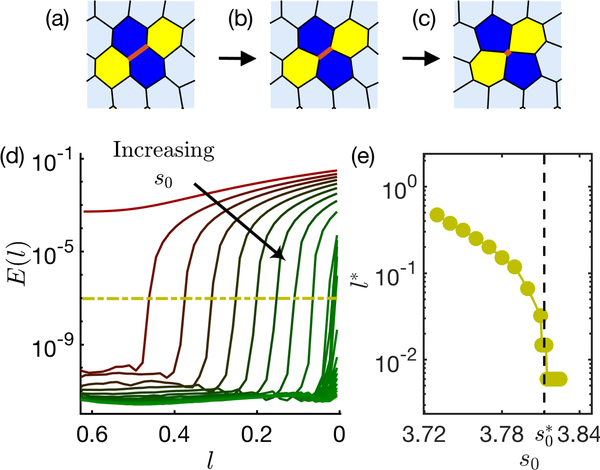
FIG. 1. Energetics of an ordered T1 transition:

(a) A T1 edge, highlighted in red, at its rest length, (b) the T1 edge shrinks to zero length (c) the T1 edge rotates by 90° and is then expanded. (d) A typical energy profile across the T1 transition plotted with respect to the T1 edge length l during of T1 junction remodelling, for s₀ 3.71, 3.72, 3.73 and 3.75 (light red to dark red). The T1 energy barrier for the lowest s₀ is the peak height (highlighted in blue vertical line).

Work by Bi et al. [15] on homogeneous disordered tessellations of cells demonstrated that the T1 energy barriers’ height depends sensitively on the target shape index (s₀) of cells. For the 2D vertex model, this energy barrier vanishes if for cells with shape parameter s₀ > 3.81. In addition, a careful numerical analysis showed that the shear modulus also vanishes at the same critical value of 3.81, which is different from the critical value of 3.722 identified in the ordered systems.

This presents an interesting open question, which is – what is the nature of the nonlinear mechanical response of ordered tissues? One possibility is that the energy barriers also vanish for s₀ > 3.722, similar to the scenario in jammed particulate matter, where there is an ordered and disordered branch to the equation of state and linear response is highly predictive of nonlinear response [16]. An alternate possibility is that the energy barriers for ordered tessellations vanish at some other value of s₀, indicating a decoupling between the linear and nonlinear response.

Understanding this point is important for several reasons. First, there are several examples where formation and maintenance of ordered 2D tessellations are important in biology, including the fruit fly wing [17], the sensory hairs in cochlea [18], and lens fibre cells in the vertebrate eye [19, 20]. In addition, scientists are investigating extensions to vertex models such as nonconfluent systems [21, 22], and vertex models with additional signaling-based dynamics [23, 24]. Therefore, it is important to understand whether we should generically expect a strong correlation between linear and nonlinear response in these extended models, or if the correlation observed the simplest disordered homogeneous vertex model may be a special feature unique to that model.

In this work we quantify the energy barriers to T1 transitions in an ordered tissue. We find that although tissues with s₀ > 3.722 are linearly unstable, T1 transitions cost finite energy up to $s_0^{*}=3.81$, due to cusps in the potential energy landscape along those trajectories in configuration space. This establishes that the linear and nonlinear response of ordered tissues are decoupled – cells cannot change neighbors even though the linear response indicates the tissue is floppy. To go beyond linear response, we develop a simple, mean-field geometric construction that describes this process and correctly quantitatively predicts features of nonlinear stabilization, and discuss implications for extensions of vertex models.

MODEL AND METHODS

To find the transition point based on T1 energy barriers, we simulate a 2D confluent monolayer using a Vertex model [1, 2, 9, 10, 15, 25–28].

Vertex models describe the energy of a 2D tissue containing N cells as

$$E_j=\sum _j^N{K}_{Aj}{\left(A_j-A_{0j}\right)}^2+K_{Pj}{\left(P_j-P_{0j}\right)}^2.$$ (1)

Here the first term represents cell volume incompressibility, and A_j and $A_{0j}$ are the actual and preferred areas of cell j. The second term models actomyosin contractility and adhesion between the cells, where P_j and $P_{0j}$ are the actual and preferred perimeter of cell j. $K_{Aj}$ and $K_{Pj}$ are the area and perimeter moduli, respectively. We consider the homogeneous case where all single-cell properties are equal ($K_{Aj}=K_A$, $K_{Pj}=K_P$, $A_{0j}=A_0$, $P_{0j}=P_0$). The energy functional in Eq. 1 can be non-dimensionalized in length $\sqrt{A_0}$ resulting an effective target shape index $s_0=P_0/\sqrt{A_0}$ which has been shown to control rigidity or glass-like transitions in such systems [15].

Cell neighbor exchanges happen through T1 transitions. A typical T1 process is shown in Fig. 1(a–c). As the T1 edge l shrinks from its rest length, l₀, (Fig. 1(a)), it eventually achieves a transition state at l = 0 with a 4-fold vertex where all 4 cells are neighbors (Fig. 1 (b)). This is followed by a 90° reorientation of the T1 edge and expansion along the new direction (Fig. 1 (c)). We find that the mechanical energy of the tissue is maximized at the transition state with the 4-fold coordinated vertex. As in previous work, we describe the difference between the initial energy and maximum energy as an energy barrier that must be overcome for cells to change neighbors. In analogy with activation energies required for diffusion in Arrhenius processes, we can then think of the T1 edge-length (l) as a reaction coordinate [15, 29].

We focus on the first part of the T1 process for the rest of this paper, as this is sufficient to compute the energy barrier (shown in blue vertical line in Fig. 1). We choose the sign convention as positive for this part of the transition, which is different from the convention used for l in work that studies both sides of the transition [15].

The difference between the peak energy E_f and the initial energy E_i gives the T1 energy barrier (Fig. 1 vertical line in blue),

$$\mathrm{\Delta }E(l)=E_f-E_i=E(l)-E(0).$$ (2)

For the bulk simulations, we use the open source cellGPU code [30]. A FIRE minimization protocol [31] is used for bulk energy minimization. The initial FIRE step, dt, is set to 0.01. The T1 protocol is such that a T1 transition forms whenever the distance between two vertices is less than a critical value, l_c. We chose l_c = 0.006 for the ordered tissue simulations.

As discussed in the ESI, we apply the same procedure to compute the transition point in disordered systems. Unlike ordered systems, which have a unique hexagonal initialization, in a disordered systems we average the energy barrier profile over different initializations. See the ESI for more details.

Recent work [32] has shown that the transition point in vertex models is unaffected by the choice of K_A. Here, we choose K_A = 100, which enforces that cells remain close to their preferred area A₀ = 1.

Many-cell system

To test the transition point of ordered tissues subject to a specific non-linear perturbation, we construct a rectangular periodic box that can accommodate an integer number of hexagons, with a length-to-width ratio of $\frac{3m}{2\sqrt{3}n}$,

where m is the number of hexagons along the vertical axis and n is the number of hexagons along the horizontal axis. We investigate small systems with N = 90 such that n = 9 and m = 10, simulated using cellGPU code.

A random edge of the ordered confluent tissue is chosen to undergo a T1 transition, and the energy profile is analyzed across different s₀ values. A typical T1 edge, with its neighbourhood, is shown in Fig. 2 (a) along with energy profiles for different s₀ values (Fig. 2(d)). For values of s₀ < 3.722, any perturbations of edge lengths costs finite energy, as illustrated by the red curve in Fig. 2(d). For values of s₀ > 3.722, we find that small perturbations of l require zero energy as previously predicted [1, 2] using linear response. This is indicated by values of E(l) near zero on the left-hand side of Fig. 2(d). A similar transition can be seen by studying the normal modes of the system. We find that the number of nontrivial normal modes with zero frequency (i.e. “zero modes”, Fig. SI 2) is zero for s₀ < 3.722 and immediately rises to 3N, where N is the number of cells in the tesselation, for s₀ slightly above 3.722.

FIG. 2. Many-cell energy profile:

(a-c) A snapshot from an ordered tessellation of 90 cells with s₀ = 3.76. A randomly chosen edge (highlighted in red), shrinks to zero length (left to right as directed by the arrows). (d) In this process, the total energy of the tissue, E, is plotted against the shrinking T1 edgelength l for increasing values of s₀ (3.72 to 3.81 in steps of 0.01 and 3.810 to 3.825 in steps of 0.001) varying from red to green. The energy cut-off is shown by yellow dash-dot line. (e) The critical edgelength l^∗ associated to the cut-off shown in (d) is plotted for each s₀ value in yellow circles. The dashed line indicates critical $s_0^{*}$ found for disordered tissues.

But as the T1 process proceeds further, the energy becomes finite at a critical lengthscale l^∗. In practice, we identify l^∗ as the point at which the energy first rises above a cutoff value of 10⁻⁷ shown by the dashed yellow line in Fig. 2(d). We find that l^∗ diminishes with increasing s₀, and drops to zero at $s_0^{*}=3.81$, which is the same value identified in disordered systems, as shown in Fig. 2(e). We note that the lowest value of l^∗ accessible in our simulations is limited by the T1 threshold length, l_c = 0.006.

We focus on T1 processes for the transition path through configuration space because they are simple to parameterize and correctly capture the rigidity transition in disordered systems [15]. However, there are other possible transition paths, including one of the 3N nontrivial zero modes identified by a normal mode analysis. However, a visual inspection of these modes shows no obvious spatial structure (Fig. SI 2(a)) and because there are so many modes with the same degenerate eigenvalue (where any linear combination of them would also be a zero mode), an exhaustive search of these possibilities is beyond the scope of this work. Nevertheless, we find that as we execute a T1 trajectory, the number of zero modes starts to decrease precisely at the cusp in the energy landscape Fig. SI 2(c), suggesting that some zero modes start to cost finite energy at that point in configuration space.

Our data is consistent with the hypothesis that the energy landscape is locally flat in many directions for s₀ > 3.772, but that any finite displacement in configuration space will cost finite energy if the displacement is large enough. More work to study many paths in configuration space would be required to confirm this hypothesis.

Single cell prediction

In both many-cell and 4-cell systems (Fig. SI 1), the ordered polygons that undergo a T1 transition start out as perfect hexagons but become pentagons as the edgelength (l) shrinks to zero (Fig. 2 (c) and Fig. SI 1 (c)). For disordered systems, the formation of a pentagon was proposed as a mean-field lower bound on the T1 transition point previously by Bi et al [15].

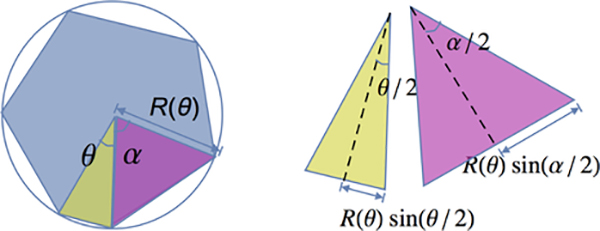
Here we construct a simple geometric ansatz to predict the T1 edgelength (l^∗) at which the energy barrier becomes non-zero. We restrict ourselves to study a polygon whose vertices lie on a circle of radius R (Fig. 3 (a)). This constraint is a simple way to enforce that the polygon remains roughly isotropic, consistent with our observations from simulations. To model the ordered case, we enforce that the polygon has six sides, one of which is constrained to shrink and subtends an angle θ at the center. We assume the remaining sides adjust themselves to be of equal length, which minimizes the remaining perimeter subject to having one constrained edge, as illustrated in Fig. 3.

FIG. 3. A geometric mechanism for formation of a uniform pentagon:

The 6-sided polygon has five sides equal to each other and one that is allowed to be different subjected to the constraints that the polygon lies on a circle and its area remains unity. The angles correspond to two different types of sides (α and θ) are highlighted in pink and green.

In the ESI we show that the minimum energy geometry in numerical simulations is slightly more complex than our simple ansatz, because the non-T1 sides of the polygon have two different edgelengths instead of one. On the other hand, if we compare the equal-edge assumption to a generalized ansatz (Fig. SI 3), the simplest one-edgelength assumption generates a lower bound on the transition length l^∗ (See Fig SI 4) that is highly predictive, as shown below.

We can then study the perimeter change of this polygon as it transforms from a uniform hexagon to a uniform pentagon. We constrain the area of the polygon to unity to account for incompressibility of cells.

The area of the polygon can be written in terms of the area of six triangles that make up the polygon. Five of them are congruent to each other, since they subtend the same angle α at the center and the sides are of length R (triangle Δ_α, labelled in violet in Fig. 3). The leftover triangle subtends angle θ at the center and will be referred to as Δ_θ.

The area constraint ensures 5Ar(Δ_α) + Ar(Δ_θ) = 1. Substituting the area in terms of angles and radius R, the radius of the circle is determined as a function of θ:

$$R(\theta )=\sqrt{\frac{2}{\sin (\theta )+5\sin (\alpha ))}}$$

where θ + 5α = 2π.

Adding all the edgelengths, the total perimeter P, of the polygon is $P(\theta )=2R(\theta )\{\sin (\theta /2)+5\sin (\alpha /2)\}=\sqrt{\frac{2}{\sin (\theta )+5\sin (\alpha )}}2\{\sin (\theta /2)+5\sin (\alpha /2)\}$.

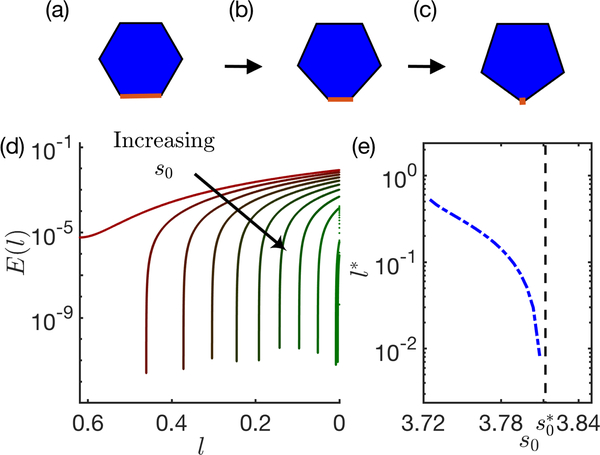
For this T1 process, the edge facing θ mimics the T1 edge that shrinks to zero as shown in Fig. 4(a). This T1 edge-length can be easily determined from θ as l(θ) = 2R(θ)sin(θ/2).

FIG. 4. Single-cell energy profile:

(a-c) For a single cell inscribed on a circle, the T1 edge (highlighted in red) shrinks to zero length (right to left as directed by the arrows). (d) In this process, the total energy E is plotted against the shrinking T1 edgelength l, for increasing values of s₀ (3.72 to 3.81 in steps of 0.01) varying from red to green. (e) The critical edgelength l^∗ associated to the drop shown in (d) is plotted for each s₀ value in blue dot-dashed line. The blue dashed line indicates critical $s_0^{*}$ found for disordered tissues.

For a cell of unit area the total vertex energy depends only on the deviation of the perimeter from its target value. The target perimeter equals the actual perimeter when the angle θ^∗ associated with a T1 edgelength l^∗ satisfies the following analytic equation:

$$P\left({\theta }^{*}\right)=P_0=\sqrt{\frac{2}{\sin \left({\theta }^{*}\right)+5\sin \left({\alpha }^{*}\right)}}2\{\sin (\frac{{\theta }^{*}}{2})+5\sin (\frac{{\alpha }^{*}}{2})\}.$$ (3)

For each value of P₀, this equation then identifies the l^∗ at which the energy barrier goes to zero, as shown in Fig. 4(d). These results are quantitatively consistent with the results for l^∗ for the 4-cell and bulk simulations, demonstrating that a very simple geometric ansatz predicts the onset of nonlinear stabilization in the ordered vertex model. All the models exhibit very similar behavior, as shown in Fig. 5, with l^∗ dropping to zero when l^∗ ∼ 3.81.

FIG. 5. Non-linear stabilization seen in ordered bulk systems can be produced in 4-cell system and single cell model:

Critical edgelength l^∗ plotted against s₀ is superimposed for both- many-cell (green circles) and 4-cell systems (magenta circles). In addition, the analytical prediction from the geometric mechanism explained in the text is shown in blue dashed line.

DISCUSSION AND CONCLUSION

We have demonstrated that the ordered ground states of the frequently-used 2D vertex model for biological tissues are stable with respect to localized cell rearrangements when the target shape parameter s₀ is between 3.72 and 3.81. This is surprising, as previous analytic calculations for the linear response highlights that the ordered states become linearly unstable for all s₀ values greater than 3.72 [1, 2].

We demonstrate this nonlinear stabilization in a full simulation of the vertex model, and also in two toy models, one of which is analytically tractable. In all three models, we find that for values of s₀ between 3.72 and 3.81, small perturbations to the structure cost zero energy, in line with previous calculations of linear response. However, there is a finite scale of perturbation at which the energy suddenly becomes non-zero. In ordered systems, we characterize this behavior in terms of the edgelength l^∗ at which the energy first becomes non-zero, and find that l^∗ decreases monotonically from the ordered edge length l₀ at s₀ = 3.72 to zero at s₀ ∼ 3.81. In the simplest analytically tractable and purely geometric model, we see that l^∗ vanishes precisely at s₀ ∼ 3.81 because that is the point at which an isotropic pentagon costs zero energy.

As discussed in the Supplementary materials, a very similar analysis can be performed on disordered configurations of the 2D vertex model. While the data is noisier due to the disorder in edge length, it is clear that in disordered tissues the smallest values of l^∗ remains on the order of the average edge length in the tissue for all s₀ < 3.81, and drops precipitously to zero for s₀ > 3.81. This Heavyside-function-like behavior is consistent with the hypothesis that disordered tissues also destabilize when it is possible for an isotropic pentagon to form at zero cost, as postulated previously [15]. An interesting direction for future work would be to carefully characterize how the statistics of short edge-lengths and l^∗s vary as a function of system size and model parameters in disordered systems, extending previous work demonstrating the importance of edge length statistics to rigidity in Vertex models [33].

Overall, this result is interesting because it suggests that unlike particulate glassy materials, where there are two branches to the equation of state associated with ordered and disordered states [16], vertex models are ultimately destabilized at the same point (or at least very nearly the same point) on the state diagram, at s₀ ∼ 3.81, regardless of the degree of disorder.

This deep connection between ordered and disordered states is only possible because the potential energy landscape of vertex models is non-analytic, or “cuspy”. Unlike most particulate matter, in vertex models there is a decoupling between the linear response and the nonlinear response. In this specific case, the energy landscape for the ordered tissue is perfectly flat in a ball of radius l₀ − l^∗ from the ordered ground state, and then rises sharply from zero starting at l^∗. This cuspy landscape has already been identified and implicated in other processes in 2D vertex models, including unexpectedly sharp interfaces between two tissue types [8]. In that work, it was demonstrated that the cuspy landscape is independent of the exact form of the model (i.e. Vertex vs. Voronoi). It was also argued that we should expect non-analytic behavior in any model with topological interactions between cells, where neighbors are defined as those that share an edge, instead of metric interactions, where neighbors are defined by how far apart they are. Additional work by some of us confirms that many types of models with topological connections, including underconstrained fiber networks, exhibit universal behavior governed by an underlying geometric incompatibility [34]. Therefore, it is interesting to conjecture that any model with topological interactions, such as those for bird flocks and certain biomimetic- and meta- materials, might have similar features with deep connections between ordered and disordered states.

Another hint at this deep connection comes from beautiful work by Moshe et al [35], who develop an analytic model based on intrinsic metrics for periodic vertex lattices. In that work, they focus on an elastic model with no rearrangements where deformations from target metrics are quadratically penalized, and they predict from first principles that for s₀ > 3.72, the energy landscape in the space of metrics is also perfectly flat. It would be interesting to see if extensions of that framework might be able to account for nonlinearities, and perhaps find some non-analyticity in the space of metrics, in order to explain non-linear stabilization in real space. If possible, our work suggests that may be a productive path towards a first-principles prediction of rigidity in a disordered system, which would be very exciting.

A related manuscript that also highlights the importance of flat energy landscapes in ordered and disordered cellular systems is the work by Noll et al [36] on isogonal modes in force-balanced tension networks. In that work, a different version of the vertex model, without a P² term in the energy functional to act as a restoring force, is coupled with myosin dynamics. The form of feedback chosen to model the myosin dynamics, which has recently been confirmed in experiments on fruit flies [23], introduces a different type of restoring force that permits mechanically stable cellular networks. Although their myosin-feedback model and our standard ordered vertex model both possess zero-energy linear modes, their zero modes must be angle-preserving while perturbations associated with our T1 transitions explicitly change angles. Given this, it would be interesting to study how the functional form of restoring forces in the energy functional for vertex models impacts the linear and nonlinear stability of cellular networks.

Finally, this work focuses on vertex models in the absence of fluctuations, i.e. at zero temperature. An interesting future direction would be to study how the effective linear response and nonlinear stability changes as a function of temperature or self-propulsion. For example, in ordered systems with 3.72 < s₀ < 3.81 one might expect that at low temperatures, fluctuations typically remain small and only probe the linear regime with no shear modulus. At higher temperatures fluctuations would regularly probe the nonlinear response, so the effective linear response has a finite shear modulus. Moreover, active or driven fluctuations with a persistence time would sample these non-linear regions in different ways, perhaps leading to very rich behavior.

Given the existence and importance of ordered cellular networks in epithelial layers in developmental systems ranging from fruit flies to vertebrates, our results might impact how we think about their form and function. Specifically, we suggest that the mechanical properties of such tissues are quite exotic, with interesting nonlinearities and possible fluctuation-induced solidification. We speculate that perhaps some biological tissues tune themselves to take advantage of these interesting properties and functions.