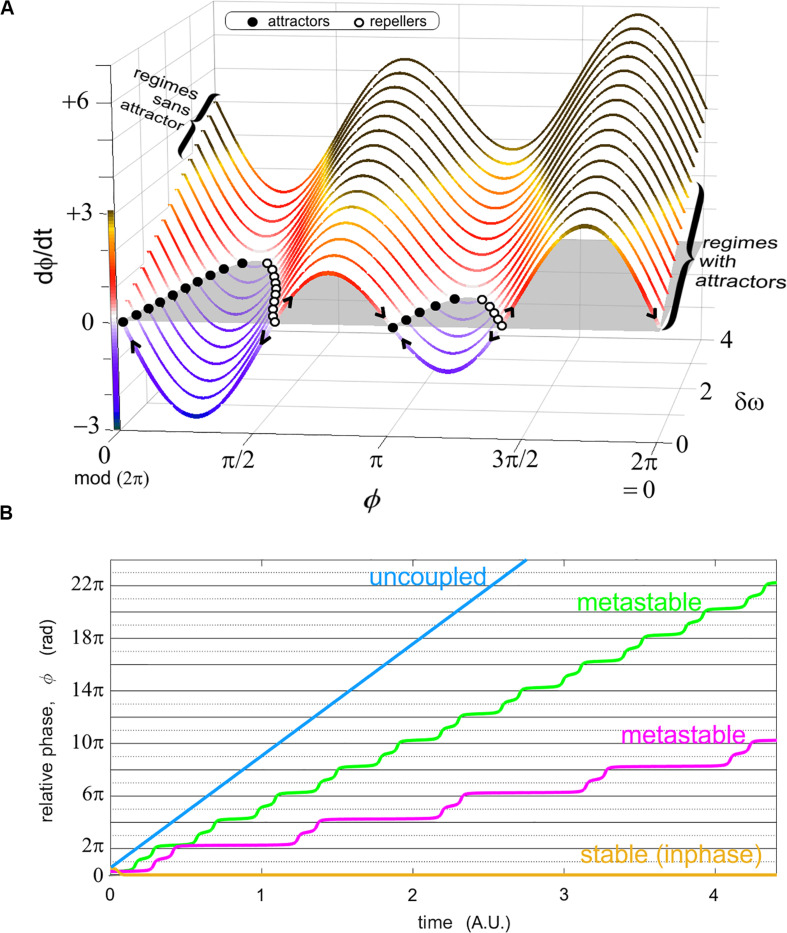
FIGURE 2.

Two representations of the relative phase as an order parameter connecting models and experiments. (A) shows the phase portrait of ϕ in the “extended” HKB model (Kelso et al., 1990) for various values of a diversity parameter δω. This graph carries regimes of coordination with attractors in the front of the figure (for modest diversity δω, shown; also when coupling is strong, not shown) and those without attractors (large diversity of the parts, shown in the back of the figure; and/or weak coupling, not shown). Attractors exist when the phase portrait (a function describing the rate of change of the relative phase as a function of itself) has values at $\frac{\text{d}\mathrm{\varphi }}{\text{d}t}=0$ (i.e., the coordination does not change over time) and a converging flow (filled black dots attracting the flow as indicated by the arrows). Stable regimes reflect a sustained cooperation among the system’s parts, but this stability also leads to inflexibility (see Kelso and Tognoli, 2007 for more details). In (B), four sample (unwrapped) relative phase evolutions over time illustrate stable coordination (yellow) where the order parameter ϕ persists at the same value (ad infinitum in models); metastability (magenta, green) with their characteristic dwells (quasi horizontal epochs, attracting tendencies near inphase, i.e., 0 rad. and antiphase, i.e., π rad. modulo 2π) and escape (wrapping); and uncoupled behavior (blue), whose relative phase grows continually with time (it approaches a linear function when the probability distribution of individual phases lacks remarkable joint phase ratios).