The Molecular Structure of Sphingomyelin in Fluid Phase Bilayers Determined by the Joint Analysis of Small-Angle Neutron and X-ray Scattering Data

Abstract

We have determined the fluid bilayer structure of palmitoyl sphingomyelin (PSM) and stearoyl sphingomyelin (SSM) by simultaneously analyzing small-angle neutron and X-ray scattering data. Using a newly developed scattering density profile (SDP) model for sphingomyelin lipids, we report structural parameters including the area per lipid, total bilayer thickness, and hydrocarbon thickness, in addition to lipid volumes determined by densitometry. Unconstrained all-atom simulations of PSM bilayers at 55°C using the C36 CHARMM force field produced a lipid area of 56 Ų, a value that is 10% lower than the one determined experimentally with the SDP analysis (61.9 Ų). Furthermore, scattering form factors calculated from the unconstrained simulations were in poor agreement with experimental form factors, even though segmental order parameter (S_CD) profiles calculated from the simulations were in relatively good agreement with S_CD profiles obtained from NMR experiments. Conversely, constrained area simulations at 61.9 Ų resulted in good agreement between the simulation and experimental scattering form factors, but not with S_CD profiles from NMR. We discuss possible reasons for the discrepancies between these two important types of data that are frequently used as validation metrics for molecular dynamics force fields.

Graphical Abstract

INTRODUCTION

Membranes play a central role in the life of a cell. Long thought to serve as a simple barrier, cellular membranes are now known to exhibit complex behaviors. The vast array of protein machinery found in membranes hints at a remarkable functionality, as nearly one third of the human genome encodes for membrane proteins.¹ Membranes are the sites of transport of ions and small molecules, where the chemical gradients that supply energy to the cell are established and maintained. Importantly, the amphiphilic lipids are responsible for providing the characteristic bilayer structure and serve as the solvent for membrane proteins. Here too, what was initially thought to be a relatively simple role is giving way to a more complicated picture. Cells have evolved a remarkable array of different lipid species,² and to a large extent the function of a membrane protein is determined by the particular coterie of lipids in its immediate environment. A major current challenge in membrane biophysics is to understand the extent to which nonrandom mixing of these various lipid species is coupled to protein function.³ At one extreme, discrete membrane domains enriched in some lipids and depleted in others can selectively incorporate certain proteins, providing a functional environment that is distinct from the globally averaged membrane environment.⁴ Detailed pictures of the lipid compositions of these domains are paving the way for well-controlled studies of chemically simplified model systems that nevertheless capture the salient details of a protein’s functional membrane environment.

Sphingomyelin (SM) is one of the most abundant lipids in mammalian plasma membranes, comprising nearly 50 mol% of the total phospholipid content of the outer leaflet.² Biologically occurring SMs are typically highly ordered, high-melting lipids that increase the structural integrity of cell membranes and reduce their permeability to water and small molecules. In addition to modifying membrane structural properties, sphingomyelin, together with cholesterol, is a major component of plasma membrane rafts, which are thought to serve as functional platforms for transmembrane signaling.⁴ Unlike saturated phosphatidylcholine (PC) lipids that are often used as substitutes for SM in model membrane studies of rafts, the interfacial region of SM possesses both hydrogen bond donors and acceptors, rendering it capable of forming both inter- and intra-molecular hydrogen bonds.⁵ The hydrogen bonding potential of SM may contribute to the exceptionally high order of these lipids. Indeed, hydrogen bonding with cholesterol has been proposed to play an important role both in raft formation⁶ and in modifying the properties of the liquid-ordered phase.⁷ Despite the clear importance of SM in biological processes, structural studies of this class of lipids are underrepresented compared to other membrane lipids.

One of the most important parameters required to accurately determine bilayer structure, lipid-lipid, and lipid-protein interactions in biomembranes is lipid packing quantified by the average lipid lateral area. In addition to playing a key role in describing membrane structure and its associated functions, knowledge of lateral lipid area is central to Molecular Dynamics (MD) simulations. The most robust determination of lipid bilayer structure, including lateral lipid area, is obtained from a joint analysis of neutron and X-ray diffraction or scattering data.^8–9 In combination with MD simulations, scattering data have been used to accurately and unambiguously determine the lipid areas of biologically relevant systems, thus reconciling long-standing differences found in the lipid literature.⁹ Here, we report experimentally determined structural parameters of palmitoyl sphingomyelin (PSM) and stearoyl sphingomyelin (SSM) from a broad array of techniques including differential scanning calorimetry (DSC), densitometry, small-angle neutron (SANS) and X-ray (SAXS) scattering, nuclear magnetic resonance (NMR), and electron spin resonance (ESR). PSM at 55 °C is analyzed further with unconstrained and area-constrained MD simulations using the CHARMM36 lipid force field. We emphasize a model-free comparison between simulation and experiment, which reveals a discrepancy between PSM bilayer structure determined by small-angle scattering and NMR.

MATERIALS AND METHODS

Materials.

N-palmitoyl-D-erythro-spingosylphosphorylcholine (palmitoyl sphingomyelin, PSM), N-stearoyl-D-erythro-spingosylphosphorylcholine (stearoyl sphingomyelin, SSM), N-palmitoyl-d31-D-erythro-spingosylphosphorylcholine (palmitoyl-d31 sphingomyelin, PSM-d₃₁), egg sphingomyelin (eSM), 1-palmitoyl-2-stearoyl-(7-doxyl)-sn-glycero-3-phosphocholine (7 Doxyl PC, 7-PC), and 1-palmitoyl-2-stearoyl-(16-doxyl)-sn-glycero-3-phosphocholine (16 Doxyl PC, 16-PC) were purchased from Avanti Polar Lipids (Alabaster, AL) and used as received. D₂O (99.96% D) was from Cambridge Isotope Laboratories (Andover, MA) and deuterium-depleted H₂O (< 1 ppm D) was from Sigma Aldrich (St. Louis, MO).

Preparation of LUVs for scattering measurements.

Phospholipid films were prepared by transferring the desired volumes of stock solutions to a glass scintillation vial with a syringe (Hamilton USA, Reno, NV). Organic solvent was removed with a gentle argon stream and mild heating, followed by further solvent removal under vacuum overnight (~12 h). Dry lipid films were hydrated to a concentration of 40 mg/mL with D₂O and then incubated at 60°C for ~ 2 h with intermittent vigorous vortexing to generate multilamellar vesicles (MLVs), followed by 5 freeze/thaw cycles between −80 °C and 60 °C. LUVs were prepared using a miniextruder (Avanti Polar Lipids) assembled with a single 50 nm pore size polycarbonate filter and heated to 50 °C. After extrusion, SANS samples were prepared by diluting 0.3 mL aliquots of the LUVs with H₂O and D₂O to produce separate 15–22 mg/mL samples in 100%, 70%, and 50% D₂O. SAXS samples were prepared separately as described above, with the exception that the dry film was hydrated with H₂O to a concentration of 20 mg/mL.

Small-angle neutron scattering (SANS).

Small-angle neutron scattering (SANS) experiments were conducted at Oak Ridge National Laboratory (ORNL), using both the CG-3 BioSANS instrument of the High Flux Isotope Reactor (HFIR) and the BL-6 extended Q-range small-angle neutron scattering (EQ-SANS) instrument of the Spallation Neutron Source (SNS). LUV suspensions were loaded into 2 mm path-length quartz banjo cells (Hellma USA, Plainview, NY) and mounted in a temperature-controlled cell holder with ~ 1°C accuracy. BioSANS data were collected at a 1.7 m sample-to-detector distance (SDD) using 6 Å wavelength neutrons (FWHM 12%), resulting in a total scattering vector of 0.04 < q < 0.4 Å⁻¹. EQ-SANS data were taken at a 2.0 m SDD with a 2.5–6.0 Å wavelength band for a total scattering vector of 0.03 < q < 0.85 Å⁻¹. Scattered neutrons were collected with a two-dimensional (1×1 m) ³He position-sensitive detector (ORDELA, Inc., Oak Ridge, TN) with 192×192 pixels (BioSANS) or 256×192 pixels (EQ-SANS). The 2D data were reduced using the Mantid software package.¹⁰ During reduction, data were corrected for detector pixel sensitivity, dark current and sample transmission, as well as background scattering from water. The one-dimensional scattering intensity as a function of the scattering vector q [q = 4π sin (θ)/λ, where λ is the neutron wavelength and θ is the scattering angle relative to the incident beam] was obtained by radial averaging of the corrected 2D data. The absolute form factor used in data analysis is given by:¹¹

$$\left|F\left(q\right)\right|=q\times \mathit{\text{sign}}\left[I\left(q\right)\right]\sqrt{\left|I\left(q\right)\right|}.$$ (1)

For both BioSANS and EQ-SANS data, the signal for q > 0.3 Å⁻¹ was dominated by incoherent scattering and was not used in subsequent analysis.

Small-angle X-ray scattering (SAXS).

X-ray scattering data for joint structural analyses were collected at the Cornell High Energy Synchrotron Source (CHESS) G-1 station. A tightly collimated (0.21×0.21 mm²) beam of 1.17 Å wavelength X-rays was detected using a 1024×1024 pixel array FLICAM charge coupled device with 71 μm linear dimension pixels. The SDD was 426.7 mm, as determined from a powder sample of silver behenate (The Gem Dugout, State College, PA). Samples were loaded in 1.5 mm quartz capillaries and held in a temperature-controlled sample rack during measurement. The X-ray scattering form factors were calculated from corrected experimental intensities using the same relationship as for neutrons (Eq. 1). An additional 4^th order polynomial was used to correct for a rise in background scattering with increasing q.¹²

Additionally, SAXS data from PSM MLV samples at 20 mg/mL were measured using a Rigaku BioSAXS-2000 home source system (Rigaku Americas, The Woodlands, TX) equipped with a HF007 copper rotating anode, a Pilatus 100K 2D detector, and an automatic sample changer. SAXS data were collected at a fixed sample-to-detector distance (SDD) using a silver behenate calibration standard. The one-dimensional scattering intensity I(q) was obtained by radial averaging of the corrected 2D image data, an operation that was performed automatically using Rigaku SAXSLab software. Data were collected in 5-minute frames with each frame processed separately to assess radiation damage; there were no significant changes in the scattering curves over time. Background scattering from water or buffer collected at the same temperature was subtracted from each frame, and the background-corrected I(q) from the individual frames was then averaged, with the standard deviation taken to be the measurement uncertainty.

Scattering Density Profile (SDP) model for SM lipids.

To jointly model SANS and SAXS data, we used a modified Scattering Density Profile (SDP) analysis appropriate for sphingomyelin structure. Briefly, the SDP model describes the underlying matter distribution in the transverse direction (i.e., normal to the plane of the bilayer) in terms of volume probability profiles of lipid component groups comprising several atoms. The Fourier transform of these volume probability profiles, when scaled by the scattering power of the group (i.e., the total neutron scattering length for SANS or atomic X-ray form factor for SAXS) and summed over all groups, gives a predicted scattering form factor that can be refined against experimental scattering data to determine the bilayer structure as described in previous publications^{8–9, 13–14} and reviews.^15–16 The atomic groupings that define the components are not arbitrary, but rather are chosen to satisfy three criteria: (1) the time-averaged matter distribution of the group should be closely approximated by an analytic function whose Fourier transform is also analytic (e.g., a Gaussian); (2) the centers of electron density and neutron scattering length density should coincide to within ~ 1 Å; and (3) the number of groups should be limited by the quantity and resolution of the scattering data. In previous publications we and others have determined that, for a disordered fluid bilayer, approximately six component groups can be resolved using a combination of neutron and X-ray scattering data.^{8–9, 13} We used MD simulations to guide the grouping of atoms because it is trivial to evaluate criteria 1 and 2 from the simulation trajectory, as demonstrated in Fig. S1 for the CH component group of PSM. Tables S1 and S2 give additional information about the SDP component groups for PSM and SSM, respectively.

Sphingomyelin atoms were parsed into six component groups for SDP analysis as shown in Fig. S2. Similarly to the parsing scheme for PC lipids,¹⁷ the headgroup choline methyls (Chol-CH₃) and N(CH₂)PO₄ moiety (PCN) are each represented by a Gaussian. In contrast to the glycerol backbone of PC, the sphingosine backbone C₄H₄X₂NO₂ (BB, also represented by a Gaussian) possesses two labile hydrogens (the amide and hydroxyl hydrogens, denoted with an X) that rapidly exchange with protium (¹H) or deuterium (²H) in the water. Given the relatively low lipid concentration of samples used for scattering measurements (~ 2 wt% lipid), we assume that the time-averaged fraction of X sites occupied by ²H is equal to the fraction of D₂O in the aqueous medium.¹⁸ The total hydrocarbon region (HC) is represented by an error function which is further subdivided into methine, methylene, and methyl groups. The trans double bond (CH) at the top of the sphingosine chain, as well as the combined terminal methyls (CH₃) at the ends of the sphingosine and N-acyl chains, are modeled as separate Gaussians such that the difference between the hydrocarbon error function and the sum of the CH and CH₃ groups gives the CH₂ distribution. Fig. S3 shows model-free PSM component volume probabilities calculated from an MD simulation, demonstrating the validity of the chosen functional forms.

Refining the positions, widths, and volumes of the functional groups together with the area per lipid in a least squares analysis results in the most likely volume probability profile for the bilayer. A number of model parameters are either directly varied in the fit or are derived from fitted or constrained parameters. We follow the naming convention used by Kučerka et al.⁹ and subsequent SDP papers: A_L is the lateral lipid area; V_L, V_HL, and V_wat are the molecular volumes of the total lipid, lipid headgroup, and water, respectively; D_B and 2D_C are the total (Luzzati) bilayer thickness and hydrocarbon thickness, respectively; D_HH is the headgroup-headgroup separation as determined by the distance between electron density maxima; and D_H1 is the difference between D_HH/2 and D_C For all Gaussian components (i.e., j = CH, CH₃, BB, PCN, and CholCH₃), z_j and σ_j represent the center and width (with z_CH3 = 0), while r_j represents a volume ratio used to determine the appropriate scale factor (specifically, r_CH = V_CH/V_CH2, r_CH3 = V_CH3/V_CH2, r_BB = V_BB/V_HL, r_PCN = V_PCN/V_HL). Finally, σ_HC is the width of the error functions representing the total hydrocarbon chain region.

Lipid volumes are critical for the SDP analysis. The total lipid volume V_L and the total bilayer (Luzzati) thickness D_B are related through the average area per lipid A_L (i.e., V_L = A_L × D_B/2). Temperature-dependent lipid volumes for PSM and SSM were independently measured as described below and constrained in the SDP analysis. The sphingomyelin headgroup volume V_HL is also a model parameter and was constrained to the value of 274 Å ³ obtained in MD simulations (this value was assumed to be independent of temperature). The difference between V_L and V_HL gives the total hydrocarbon volume V_C. The partitioning of the headgroup and hydrocarbon volumes between their constituent fragments was allowed to vary in the fit subject to soft (quadratic) restraints as previously described.⁹

Electron spin resonance (ESR).

Samples for ESR were prepared by mixing 13 μmol of PSM in chloroform with 65 nmol of a lipid spin probe (16-PC or 7-PC) in chloroform. Bulk solvent was removed with a nitrogen stream for ~ 30 min, followed by dring under vacuum for ~ 1 h at 55°C. The dry film was hydrated with 520 μL of H₂O and incubated for 1 h at ~ 50 °C, vortexing every 15 min. Samples were subjected to 5 freeze/thaw cycles between liquid nitrogen and a water bath at ~ 50 °C. Each sample was then divided into separate aliquots for MLV, LUV, and small unilamellar vesicle (SUV) samples. To generate LUVs, a 220 μL sample aliquot was extruded through a single 50 nm pore size polycarbonate filter 31 times at 50 °C. To generate SUVs, a 220 μL sample aliquot was sonicated in a bath sonicator at 50 °C for ~ 5 min and then gently centrifuged to bring down droplets from the sides of the sample tube. Sonication was then repeated for a total of ~ 20 min until the sample appeared translucent. Aliquots (20 μL) of the LUV and SUV samples were set aside for DLS. The LUVs, as well as 80 μL of the original MLV sample, were diluted to 200 μL with H₂O and centrifuged (140,000×g) at 4 °C for 1 h. The SUVs were centrifuged (140,000×g) at 22 °C for 2 hrs. Supernatant was then removed from each sample, and the pellets were diluted with 3–6 μL of H₂O. The concentrated samples were loaded into open-ended 1.5–1.8×100 mm glass capillaries (Kimble Chase Life Science, Rockwood, TN). After flame sealing one end of the capillary, the sample was spun down with low speed centrifugation, and the other end was then flame sealed. For measurement, the sealed capillary was placed into a 2 mm NMR tube containing light mineral oil to ensure proper temperature control. ESR spectra were recorded on a Bruker EleXsys-II E500 CW EPR spectrometer operating at X-band frequency (9.4 GHz). The spectrometer settings for all samples were as follows: center field = 3362.9 G, sweep width = 100 G, microwave power = 0.3170 mW, modulation frequency = 100 kHz, modulation amplitude = 0.8 G, resolution (points) = 1024. Reported spectra are the average of 4–16 scans depending on the signal intensity.

ESR first derivative spectra were integrated once to obtain the corresponding absorbance spectrum, and then a second time to obtain a total area which is proportional to the total amount of spin probe in the sample (Fig. S4); the areas were used as normalization factors for both the first derivative and absorbance spectra to correct for sample-to-sample differences in concentration. Normalized spectra were then re-centered to align the second absorbance peak at 3320 G. Model-free order parameters were determined from a lineshape analysis of normalized and centered ESR spectra which was automated using custom code written in Mathematica v. 11.0 (Wolfram Research, Inc.). As shown in Fig. S4, the inner and outer hyperfine splittings of the first derivative spectrum (2A_min and 2A_max, respectively) were determined by fitting the corresponding absorbance spectrum as a sum of Lorentzians:

$$A\left(B\right)=\sum _{i=1}^N{C}_i\frac{{\text{Γ}}_i}{{\left(B-B_i\right)}^2+{\text{Γ}}_i{}^2},$$ (2)

where B is the magnetic field strength and the C_i, Γ_i and B_i are fit parameters. Typically, N = 50–70 produced a (purely phenomenological) analytical function A(B) that very closely approximated the raw data, as demonstrated by the residual plots in Fig. S4 (note that residuals are expanded by a factor of 10⁵ relative to the corresponding data). Zeroes in the second derivative of A(B) were then used to determine the peak positions in the first derivative spectrum that define 2A_min and 2A_max. The uncorrected (apparent) order parameter S_app is given by:

$$S_{app}=\frac{A_{max}-A_{min}}{A_{zz}-0.5\left(A_{xx}+A_{yy}\right)},$$ (3)

where A_xx, A_yy and A_zz are the principal components of the hyperfine tensor. These constants are obtained from the first derivative spectra of the dilute probe embedded in a crystal and are often referred to as “single crystal values”. Here, we use values for 7-PC and 16-PC previously reported in the literature,¹⁹ namely (A_xx, A_yy, A_zz) = (5.4, 5.4, 33.4 G) for 7-PC and (5.0, 5.0, 32.6 G) for 16-PC. We note that because these values are constants that appear in the denominator in Eq. 3, they act as a scale factor for the difference in the hyperfine splittings measured directly from the spectra; therefore their precise values do not affect the trends in order parameter that we use to interpret relative differences in the fluidity of vesicles as a function of size and temperature. Finally, the molecular-frame order parameter S_zz is calculated as:²⁰

$$S_{zz}=1.069\cdot S_{app}-\mathrm{0.051.}$$ (4)

Solid state ²H NMR.

Multilamellar dispersions of 50 wt% PSM-d₃₁ were prepared as follows. A lipid film was prepared by dissolving 26 mg PSM-d₃₁ powder in chloroform, followed by removal of the bulk solvent on a rotary evaporator and overnight vacuum. The film was hydrated with 2 mL degassed, deuterium depleted water (DDW) preheated to 50 °C and then incubated at 50 °C for 2 h with intermittent vortexing. The suspension was lyophilized, weighed, and rehydrated with 2 mL DDW. This cycle was repeated two additional times to reduce the amount of ²HHO from its naturally abundant level. The final rehydration was in 26 μL DDW, followed by five freeze/thaw cycles between a −80 °C and 50 °C. The sample was then transferred to a 5 mm NMR tube and sealed with a cap and Teflon tape for measurement. LUVs were prepared using a miniextruder (Avanti Polar Lipids) assembled with a single 50 nm pore size polycarbonate filter and heated to 50 °C. The LUVs were diluted to 200 μL with DDW and centrifuged (140,000×g) at 4 °C for 1 h. Supernatant was then removed from each sample, and the pellets were diluted with additional DDW to 50 wt%. During the experimental process, aliquots of the sample were tested using dynamic light scattering to verify LUV size integrity.

Solid state ²H NMR experiments were performed on a homebuilt NMR spectrometer operating at 46.0 MHz with a 7.05 T superconducting magnet (Oxford Instruments, Osney Mead, UK),²¹ equipped with an in-house assembled programmable pulse generator and a dual-channel digital oscilloscope (R1200 M, Rapid Systems, Seattle, WA) to acquire signals in quadrature. Sample temperature was regulated to within ± 0.5 °C with a temperature controller (1600 Series, Love Controls, Michigan City, IN). A phase-alternated quadrupolar echo sequence (90°_x-τ−90°_y-aquire-delay) was used to eliminate spectral distortion due to the receiver recovery time.²² The following instrument parameters were used: 90° pulse width = 3.7 μs; separation between pulses τ = 50 μs; delay between pulse sequences = 1.0 s; sweep width = ± 100 kHz; and number of scans = 8,192. The ²H NMR spectra acquired are a superposition of powder patterns from all positions of isotopic labeling in the N-acyl chain of PSM-d₃₁.²³ Each powder pattern has a pair of most intense peaks split in frequency by Δv_r that relates to an order parameter S_CD for the C-²H bond in a chain segment according to a standard expression.²⁴ Further, spectra can be analyzed in terms of moments,²³ which are defined as:

$$M_n\equiv \frac{{\int }_{-\infty }^{\infty }{\left|\omega \right|}^{n}f\left(\omega \right)d\omega }{{\int }_{-\infty }^{\infty }f\left(\omega \right)d\omega },$$ (5)

where M_n is moment of order n, ω is the angular frequency, and f(ω) is the spectral line shape. For MLV in the liquid crystalline state each powder pattern has a pair of most intense peaks split in frequency by Δv_r that relates to an order parameter S_CD for the C-²H bond in a chain segment according to a standard expression.²⁴ The first moment corresponds to the average order parameter according to the expression $M_1=\pi {\chi }_Q\overline{\left|S_{CD}\right|}/\sqrt{3}$,²³ where the quadrupolar coupling constant is, χ_Q = 1.68 kHz. Although the relationship to average order is inapplicable to MLV in the gel phase and to LUV in either gel or liquid crystalline phase, moments are still sensitive to phase transitions.

Densitometry.

Samples for densitometry were prepared by dispensing SM stock solution in chloroform/methanol (98/2 v/v) into a clean, preweighed glass vial. Bulk solvent was then removed with a nitrogen stream and gentle heating, followed by overnight vacuum pumping at room temperature. The vial was then weighed, and the lipid mass (20–40 mg) was calculated to within 0.1 mg. H₂O (1.5 mL) was added to the vial and the weight recorded to within 0.1 mg. The sample was hydrated at 60 °C for 2 h with intermittent brief sonication in a Bransonic 5510 ultrasonic bath (Emerson, St. Louis, MO) to disperse the lipid. Density measurements were performed with an Anton Parr (Ashland, VA) DMA 5000 M vibrating tube density meter. Lipid molecular volume V_L was calculated using the relationship:²⁵

$$V_L=\frac{M_L}{0.6022{\rho }_S}\left[1+\frac{m_W}{m_S}\left(1-\frac{{\rho }_S}{{\rho }_W}\right)\right],$$ (6)

where M_L is the molar mass of the lipid, ρ_S and ρ_W are the measured densities of the sample and H₂O, respectively, m_S is the mass of the dry lipid, and m_W is the mass of H₂O added to the dry lipid. Densitometry data for PSM and SSM are shown in Fig. S5.

Differential scanning calorimetry (DSC).

MLV samples for DSC were prepared by adding 0.8 mL H₂O to ~ 4 mg dry lipid powder, then vortexing vigorously to disperse the lipid. The sample was hydrated at 60 °C for 2 h with intermittent vortexing, followed by 5 freeze/thaw cycles between a −80 °C and 60 °C. DSC measurements were performed using a TA Nano DSC (TA Instruments, USA, New Castle, DE). The sample was first annealed with two complete temperature cycles between 5 °C to 55 °C at a scan rate of 1 °C/min. A production cycle was then collected from 5 °C to 55 °C at a scan rate of 0.2 °C/min. DSC data for PSM and SSM are shown in Fig. S5.

Molecular Dynamics simulations.

PSM bilayers for MD simulations were constructed using the CHARMM-GUI Membrane builder.^26–29 Each bilayer had a total of 200 lipids (100 lipids per leaflet) and was hydrated with 45 waters per lipid molecule. One system was constructed with the default area per lipid for PSM in CHARMM-GUI (55.4 Ų) and simulated in the NPT ensemble, allowing for the bilayer area to converge to its equilibrium value. Five additional simulations were run with constrained areas per lipid of 59, 61, 61.9, 63 and 65 Ų, and were simulated in an NPAT ensemble, keeping the lateral bilayer area fixed while allowing for the z-dimension of the simulation box to vary.

All simulations were performed with the NAMD software³⁰ and the CHARMM36 force field for lipids.^31–33 Each system was initially equilibrated with the CHARMM-GUI equilibration protocol, followed by a production run of 350 ns for the unconstrained simulation, and 180–200 ns for the constrained-area simulations. A cutoff of 10–12 Å was used for non-bonded and short-range electrostatic interactions with the VdwForceSwitching option turned on. Particle Mesh Ewald with grid spacing of 1 Å was used for long-range electrostatics. Constant temperature of 55 °C was maintained with a Langevin thermostat. Constant pressure of 1 atm was achieved with the Langevin piston Nose-Hoover method with a 200 fs period and 50 fs decay. All simulations were run with a 2 fs time-step and the rigidbonds option set to all.

For analysis, the last 100 ns of each trajectory were first centered on the average position of the terminal methyl carbons of all PSM molecules. Number density profiles of all PSM and water atoms were calculated with the Density Profile tool in VMD with a resolution of 0.2 Å.³⁴ Ensemble-averaged acyl chain order parameters for each carbon were obtained with in-house Tcl and MATLAB scripts using the formula:

$$S_{CD}=\left|\frac{1}{2}\langle 3{\cos }^2\Theta -1\rangle \right|,$$ (7)

where Θ represents the angle between a CH bond and the bilayer normal assumed to be the z-dimension of the simulation box.

Model-free comparison of experimental and simulation scattering data.

Unconstrained and constrained-area simulations were evaluated against experimentally determined scattering data sets in a model-free comparison as previously described.³⁵ Briefly, the time-averaged real-space atomic number density profiles were directly converted to reciprocal space scattering data by Fourier transform, thereby avoiding assumptions associated with models. Calculated scattering form factors on an absolute scale were then compared with experimentally determined form factors through a chi-square goodness-of-fit criterion:

$${\chi }^2=\frac{1}{N_q-1}\sum _{i=1}^{N_q}{\left(\frac{|F_s\left(q_i\right)|-k_e|F_e\left(q_i\right)|}{{\sigma }_e\left(q_i\right)}\right)}^2,$$ (8)

where F_s(q) and F_e(q) are the simulated and experimentally determined form factors, σ_e(q) is the experimental uncertainty, N_q is the number of experimental data points, and k_e is a scale factor that minimizes χ².¹²

For the model-free evaluation of MLV samples, the form factors in Eq. 8 were replaced with scattering intensities I(q). To compute I_s(q), the simulation form factor was modified by a structure factor S(q) to account for Bragg scattering between stacked bilayers:

$$I\left(q\right)=q^{-2}S\left(q\right){|F_s\left(q\right)|}^2,$$ (9)

where S(q) depends on the average number of stacked bilayers, the distance between bilayers, and a parameter related to bilayer undulations.³⁶ For each simulation/experiment comparison, the structure factor parameters were optimized to minimize χ² as described in ref.³⁷.

RESULTS

Structure of SM from joint SANS/SAXS analysis of LUVs.

Small-angle neutron and X-ray scattering have proven instrumental in the determination of bilayer structure.^15–16 The quantification of structural parameters from the data requires a real-space bilayer model, where lipid component groups are represented by probability distributions, whose scattering profile is compared to the raw scattering form factor in an iterative fitting procedure. The fitting routine can be applied simultaneously to multiple differently-contrasted data sets of nominally the same bilayer. Since X-rays and neutrons interact differently with a sample, SANS and SAXS themselves represent different contrasts. Moreover, additional contrast conditions can be achieved with SANS by selectively deuterating part of the sample (water and/or lipids) due to the unique interactions of neutrons with ¹H and ²H. In general, the more contrast conditions are used to refine the real-space bilayer model, the more robust are the structural parameters obtained in the analysis.

For both PSM and SSM, we measured X-ray scattering form factors in H₂O and neutron scattering form factors in 100, 70, and 50% D₂O. We also measured the SANS form factor of PSM-d₃₁ in 100% D₂O (not shown). Together, these data sets comprise two different radiation contrasts, three different external (solvent) contrasts, and in the case of PSM, one internal (bilayer) contrast. All of these data sets were refined jointly against a single model of the bilayer’s matter distribution to provide a robust determination of the bilayer structure, including the average area per lipid and various bilayer thicknesses. The modeling approach assumes volume incompressibility and derives the average area per lipid from the lipid volume (see Table 1 and Fig. S5) and leaflet thickness calculated as half the bilayer (Luzzati) thickness (D_B in Table 1). Because of the relatively high main transition temperatures of PSM (42°C) and SSM (45°C), we collected data at only two fluid phase temperatures for each. Figure 1 illustrates the determination of PSM bilayer structure at 45°C: Fig. 1a shows SANS data for different external and internal contrasts, Fig. 1b shows SAXS data, Fig. 1c and 1d show electron density and neutron scattering length density profiles, respectively, and Fig. 1e shows the underlying volume probability profile.

Table 1.

Structural parameters of PSM and SSM obtained from joint analysis of SAXS and SANS data, and those from MD simulation with a constrained area per lipid of 61.9 Ų. Parameter symbols are defined in Materials and Methods. Uncertainty of free parameters is estimated to be 2%.⁹

Parameter	SSM		PSM
	Experiment		Experiment		Simulation
T [°C]	55	65	45	55	55
Vwat [Å3]**	30.2	30.3	30.2	30.3	30.5
VL [Å3]**	1226.8	1237.1	1151.6	1161.7	1172.4
VHL [Å3]**	274	274	274	274	275.1
rBB*	0.34	0.33	0.36	0.37	0.37
rPCN*	0.33	0.33	0.4	0.4	0.35
rCH3*	2.14	2.06	1.99	2	2.12
rCH*	1.12	1.09	1.14	1.13	1.03
DB [Å]	39.3	38.1	38.4	37.5	37.9
DHH [Å]	40	39.4	38.9	37.8	38
2DC [Å]	30.5	29.7	29.3	28.7	29
DH1 [Å]	4.77	4.85	4.8	4.55	4.5
AL [Å2]	62.5	64.9	60.0	61.9	61.9
zBB [Å]	14.7	14.2	14.6	14.1	15.8
σBB [Å]	2.1	2.03	2.55	2.36	2.44
zPCN [Å]	20.1	19.7	19.5	18.9	19.2
σPCN [Å]	2.5	2.48	2.24	1.89	2.52
zCholCH3 [Å]	23.7	23.1	21.7	22	20.5
σCholCH3 [Å]**	2.95	2.95	2.95	2.95	2.94
zCH [Å]	15.8	15.3	14.8	14.9	14
σCH [Å]**	2.54	2.54	2.54	2.54	2.48
σHC [Å]*	2.79	2.76	2.81	2.8	2.51
σCH3 [Å]	3.05	3.38	2.83	3.159	3.19

^**constrained parameter;

^*restrained parameter

Figure 1. Joint SDP analysis of PSM scattering data at 45°C.

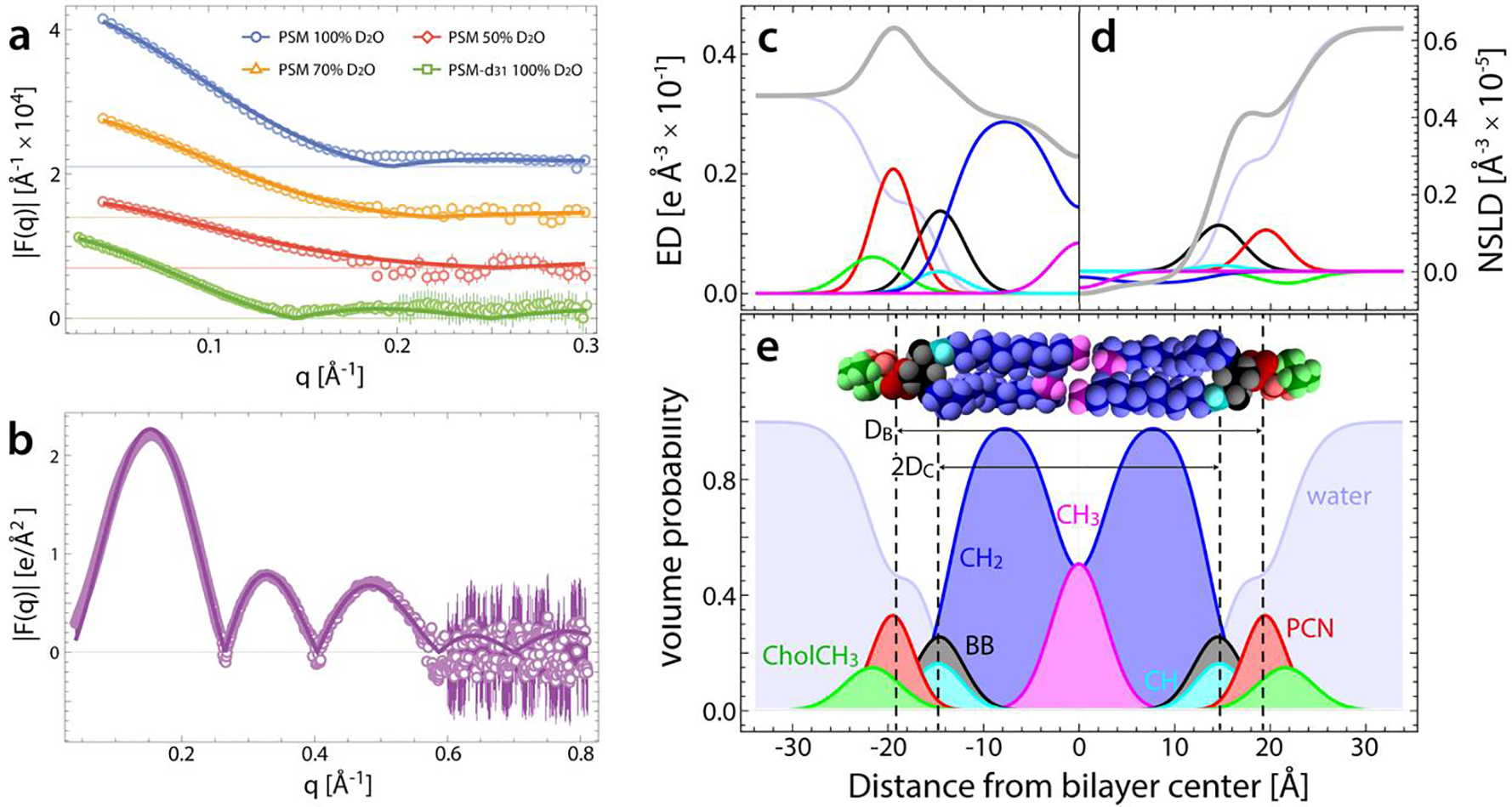
(a,b) Small-angle neutron (a) and X-ray (b) scattering data from 50 nm LUVs (open symbols), and corresponding fits (lines) to the SDP model (see text for details). SANS data were obtained at three external contrasts and one internal contrast (not shown). (c-e) Electron density (c) and neutron scattering length density (d) distributions (ED and NSLD, respectively) for PSM component groups, calculated from volume probability distributions shown in (e). The total SLD profiles in c and d (gray lines) are the sum of the component SLD profiles (colored lines). Fourier transform of the total SLD profiles yields the analytical scattering curves for 100% D₂O SANS data in panel a and SAXS data in panel b.

Table 1 gives a complete list of the structural parameters for PSM and SSM. At 55°C, SSM is thicker than PSM, as expected from the two additional carbons in the N-linked chain in SSM. With increasing temperature, both bilayers become thinner and their areas per lipid increase.

Order parameters from ²H NMR of PSM MLVs and LUVs.

²H NMR spectra for deuterated PSM (PSM-d₃₁), prepared as MLVs and LUVs, were obtained over a range of temperatures from 30 °C to 65 °C. Below 38 °C, spectra for both types of preparation are broad and relatively featureless (Fig. S6). This shape reflects the slow rotational diffusion undergone by the rigid, all-trans palmitic acid chains on PSM-d₃₁ in the gel state. Above 38 °C, the spectra (Fig. S6) are dramatically reduced in width by fast axial rotation associated with rapid isomerization about C-C bonds in melted chains. The resulting shape in the case of MLVs is a signature for the lamellar liquid crystalline phase²³ where spectral components for some of the methylene groups (and the methyl group) become identifiable. Although spectral narrowing also occurs in LUVs above 38 °C (Fig. S6), distinct spectral components are not observed. This is likely due to the curvature of LUVs, where lateral diffusion and vesicle tumbling move lipids between bilayer regions at different orientations on the NMR time scale, smearing out individual spectral components. Although the LUV line shape is not directly amenable to segmental analysis, moment analysis nevertheless provides a sensitive indication of bilayer phase.

Figure 2 shows the first moments obtained by ²H NMR spectroscopy for LUVs and MLVs. The data shows that the phase transition (identified as the mid-point of an accompanying dramatic drop in value of moment) of PSM in the MLVs and LUVs is 38.0 ± 0.5 °C. The lower melting temperature of the PSM-d₃₁ vesicles relative to their protiated counterparts measured with DSC (Fig. S5) is consistent with previous observations of the effect of different isotopes on bilayer state transitions.^38–39 The LUV phase transition is broadened due to the lack of cooperativity between bilayer stacks in MLV phases.⁴⁰ However, the effects of cooperativity near the phase transition are found to diminish above 40 °C for both systems. We emphasize that the reduction in moments for LUVs compared to MLVs is due to motional averaging associated with vesicle curvature, and not a result of substantially greater disorder.⁴¹

Figure 2.

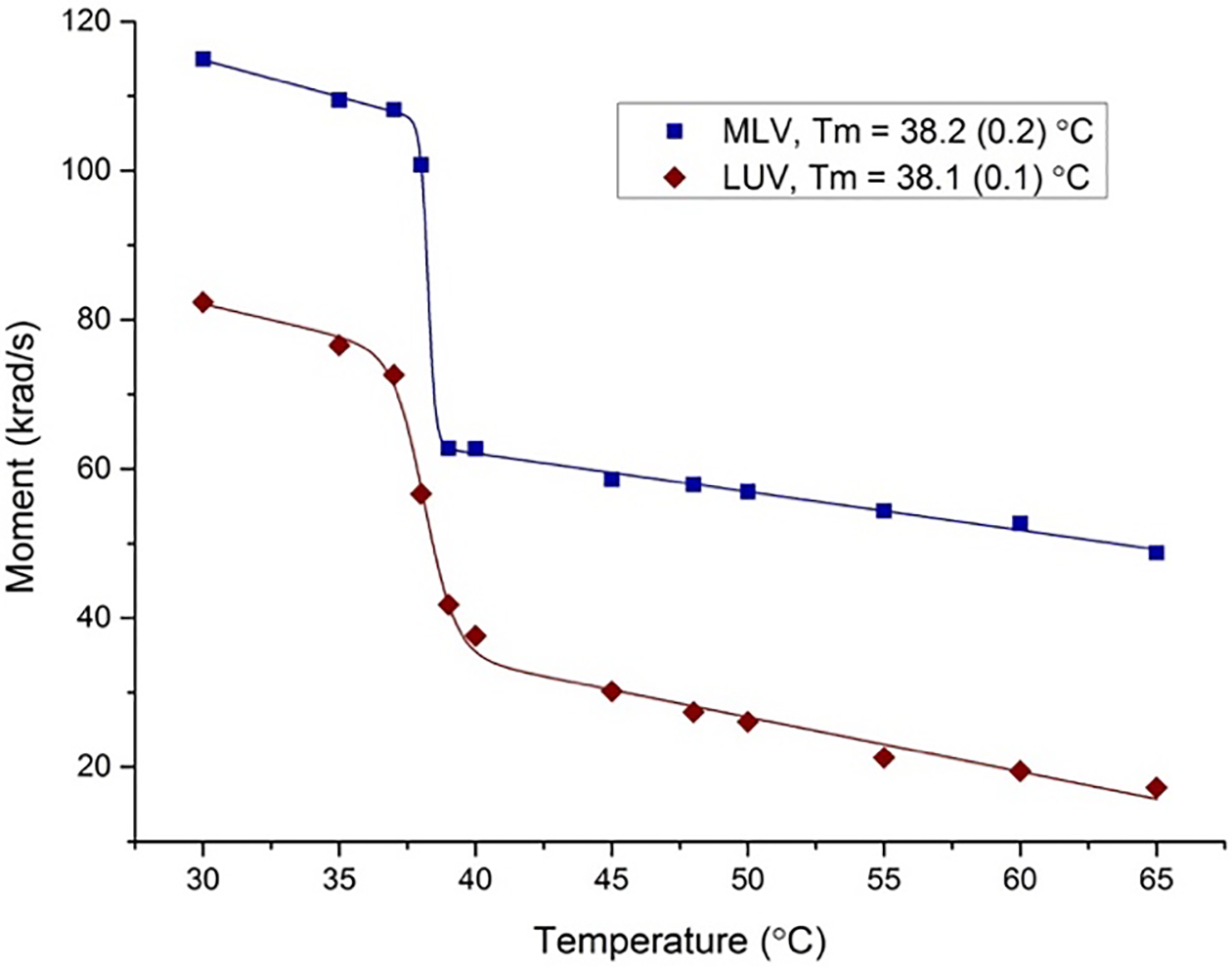
First moment plot of PSM MLV (blue) and LUV (red) samples determined from NMR as a function of temperature. We estimate a reproducibility of ± 1% for moments and ± 0.5 °C for temperature, respectively.

For PSM-d₃₁ in MLVs, distinct quadrupolar splittings were observed for many of the acyl chain segments at temperatures above 40 °C (Fig. S6). Using a FFT depaking algorithm,⁴² we calculated the order parameter profile for PSM-d₃₁ at 55 °C (Fig. 3c, solid gray squares). Experimentally, order parameters are traditionally plotted from the highest order to the lowest order unless specific assignments are known. It is assumed that carbon segments towards the aqueous interface are more ordered and become increasingly disordered towards the end of the chain at the center of the bilayer. This assumption is valid and easily applied to the terminal methyl group and nearby methylene groups in the lower portion of the chain (C12-C16). However, tight packing in the vicinity of the aqueous interface can constrain orientation and result in reduced order parameters, i.e., a conformation placing a C-²H bond closer to the magic angle (θ = 54°54′) relative to the bilayer normal will reduce the time averaged second order Legendre polynomial that defines the order parameter irrespective of the amount of angular fluctuation. The second carbon segment on the palmitoyl chain of PSM-d₃₁, where distinct order parameters are observed for the two deuterons in the methylene segment, is an example.⁴³ These individual deuterons are identified in the ²H NMR spectra for the perdeuterated chain on the basis of integrated intensity (i.e., they have half the area of a methylene peak and a third of the area of the methyl peak) and their order parameters are included in Fig. S7A. The remaining methylene groups in the upper portion of the chain (C3-C11) are indistinguishable by area considerations and are assigned according to decreasing order. Where multiple methylene groups form a composite peak, in particular, the peak is deconvoluted into signals attributed to separate methylene groups. For comparison with MD simulations, experimental order parameters are plotted in decreasing order (i.e. as a function of sort index).

Figure 3. Model-free comparison of experimental and simulated data.

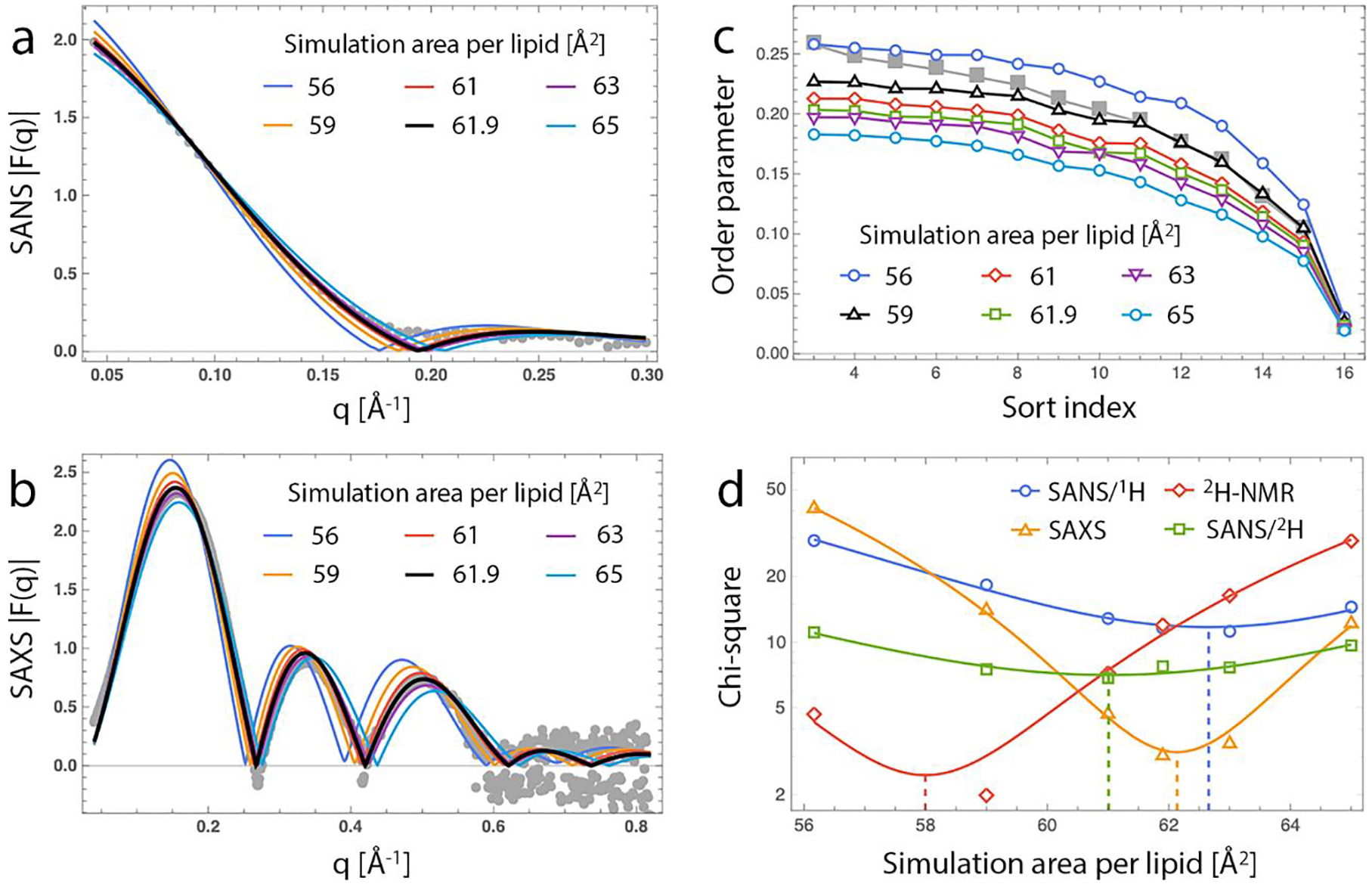
Experimentally determined data sets (solid gray symbols) are compared with corresponding data calculated from unconstrained and area-constrained MD simulations (solid lines) with areas per lipid shown in the legend: SANS form factor for PSM in 100% D₂O (a), SAXS form factor (b); NMR segmental order parameter profile (c). In each plot the simulation data that most closely matches the experimental data (as judged from a chi-square metric, see panel d) is shown in black. (d) Chi-square values plotted on a log scale for the model-free comparison of simulated and experimental data. Each set of chi-square values was fit to a parabola; the solid dashed line shows the minimum of each fit. SANS/¹H and SANS/²H refer to PSM and PSM-d₃₁, respectively, both in 100% D₂O. Errors for NMR order parameters are estimated to be ± 1%.

Model-free validation of simulated PSM bilayers.

Small-angle scattering and NMR data are routinely used in the refinement and validation of force field parameters for MD simulations of lipid bilayers. To facilitate the comparison between simulation and experiment and evaluate the robustness of the sphingomyelin parameters in one of the most widely used force fields, CHARMM36, we performed all-atom MD simulations of a PSM bilayer at 55°C. In the absence of any constraints the bilayer reached an equilibrium area per lipid of 56.2 Ų, 10% lower than the area per lipid obtained from joint analysis of the SANS and SAXS data (Table 1). To compare simulation and experiment more directly, we calculated the 100% D₂O SANS and SAXS scattering form factors of the simulated bilayer from the bilayer’s number density profile as described in Materials and Methods. Consistent with the observed trend in the area per lipid, the simulated form factors showed scattering minima at lower q values compared to the experimental data (Fig. 3a and Fig. 3b, solid dark blue lines), indicating a thicker bilayer and tighter lipid packing in the simulation.

A point-by-point comparison of the simulation and experimental form factors provides a model-free approach for quantifying the similarity between simulation and experiment.³⁵ We thus sought to use this model-free analysis to identify the lipid packing at which the two techniques agree. To this end, we ran a series of simulations of the same PSM bilayer at 55 °C but with the average area per lipid fixed to either 59, 61, 61.9, 63 or 65 Ų. The SANS and SAXS form factors of each simulated bilayer (Fig. 3a and Fig. 3b, solid lines) were compared to the raw experimental data (Fig. 3a and Fig. 3b, gray circles) and the similarity between them was quantified by the corresponding chi-square or goodness-of-fit parameter (Fig. 3d). Taking the minimum of a parabola fit to the chi-square vs. simulated area data (Fig. 3d, solid lines) to be the implied best area, the model-free analysis indicated best agreement for SAXS LUV data at a simulated area per lipid of 62.1 Ų, and a best agreement for SANS data from PSM and PSM-d₃₁ at simulated areas per lipid of 62.7 Ų and 61.0 Ų, respectively. Additionally, two independent SAXS data sets for PSM in H₂O at 55 °C showed best agreement with the 63 Ų constrained-area simulation, and areas per lipid of 62.8 Ų and 63.9 Ų implied by quadratic fits to the chi-square data (Fig. S9). In other words, all scattering data sets had best agreement with simulated bilayers over a relatively narrow range of 61–64 Ų. Indeed, the structural parameters from the fixed-area simulation at 61.9 Ų were in excellent agreement with the results from the joint analysis of the SAXS/SANS data (Table 1).

We then investigated how well the simulation force fields capture the structure of PSM determined by NMR by calculating the N-acyl chain order parameters from the simulated bilayers. Figure 3c shows the respective order parameters sorted from highest to lowest (see Fig. S7 for the data vs. carbon number from the simulations). The experimentally determined lipid order was lower than that calculated from the unconstrained simulation, indicating a looser lipid packing in the experimental system, similar to the scattering data. Interestingly however, a model-free comparison between the NMR data and the order profile of each constrained MD simulation revealed best agreement between NMR and a lipid area of 58 Ų, rather than the 61.9 Ų obtained from the scattering experiments (Fig. 3d). Possible reasons for this discrepancy are outlined in the Discussion section.

ESR of PSM for vesicles of different curvature.

While vesicles used in scattering experiments were extruded through 50 nm pores, the MLVs measured with NMR were micron-sized. We therefore sought to examine the effects of curvature on the order parameter of the lipids. To this end, we used ESR spectroscopy, which provides information about lipid order through the spectral characterization of a paramagnetic probe incorporated into the bilayer. The probe—a PC lipid with a fully saturated 16C sn-1 chain and nitroxide radical attached to either the 7^th (7-PC) or 16^th (16-PC) carbon of the 18C sn-2 chain (structures shown in Fig. 4)—absorbs energy when placed in a magnetic field at a specified frequency. Subsequent analysis of the spectral distances in the resulting profile quantifies the probe’s motions, thereby informing on lipid motions in the probe’s immediate environment (see Methods). Moreover, depending on the location of the nitroxide label, information about the lipid order at different depths within the bilayer can be obtained.

Figure 4. Average order parameter of PSM in vesicles of increasing curvature determined by ESR as a function of temperature.

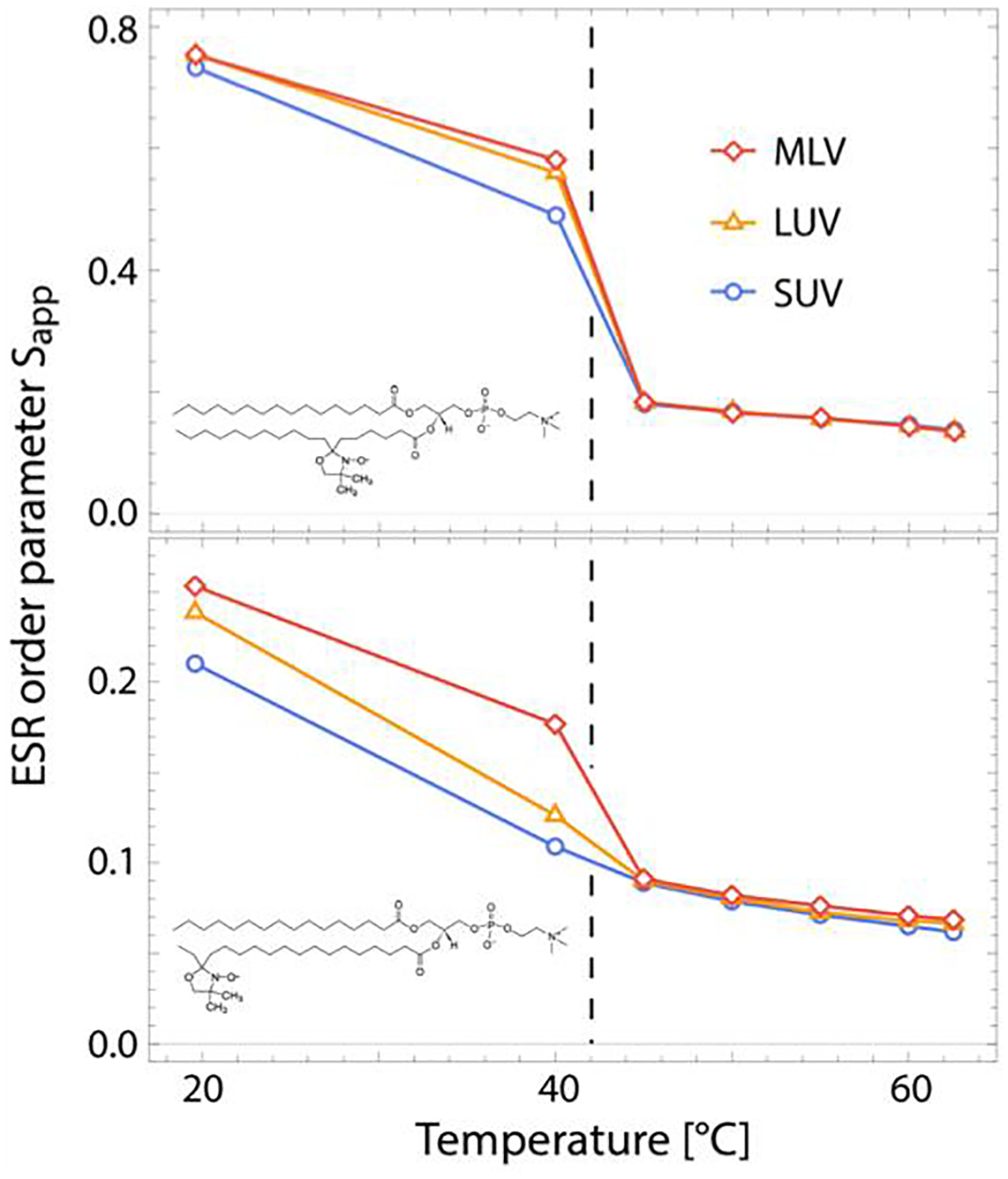
Shown are data for two different probes, 7-PC (top) and 16-PC (bottom), in micron-sized MLVs, extruded LUVs with a diameter of ~ 85 nm, and sonicated SUVs with a diameter of ~ 50 nm. Schematics of the structure of each probe are shown in the lower left corner of the respective plots. Reproducibility of ESR order parameters are < 1%.

Figure 4 shows the apparent order parameter of 16-PC and 7-PC in PSM vesicles of different size (and hence, bilayer curvature) as a function of temperature (sonicated SUVs had a diameter of ~ 50 nm as determined by DLS, while extruded LUVs had a diameter of ~ 85 nm). Below the bilayer’s melting temperature large differences are observed between the three samples, with the order of both probes decreasing with increasing curvature. In contrast, in the fluid state the probes showed a similar degree of order in all vesicles (small differences following the same trend as in the gel state can be seen only in 16-PC at higher temperatures).

DISCUSSION

The SDP model has its roots in the pioneering work of Wiener and White, who first described the joint analysis of neutron and X-ray diffraction data for determining bilayer structure.^{8, 13–14} Kučerka and coworkers⁹ modified Wiener and White’s composition space method to utilize the continuous form factor obtained from small-angle scattering experiments (rather than the discrete structure factors obtained from diffraction experiments), allowing for data collection on unilamellar vesicles at full hydration and thus circumventing the inherent difficulties in making fully hydrated oriented bilayers for diffraction measurements.⁴⁴ Variations of the SDP model have been developed for analysis of neutron and X-ray reflectometry data from supported bilayers,^45–46 multilamellar vesicles,⁴⁷ asymmetric bilayers,⁴⁸ and membranes containing proteins,^49–50 small molecules,⁵¹ or mixtures of lipids.⁵².

In developing the SDP model, an important innovation of Kučerka et al.⁹ was the use of MD simulations to optimize the parsing of the lipid molecule into quasimolecular fragments, which increased the accuracy of the modeling approach. For each class of lipids, a parsing scheme must be designed that satisfies certain criteria (outlined in Materials and Methods). SDP models have now been constructed for PC,¹⁷ PG,^{11, 25, 53} PE,¹² PS,¹¹ cardiolipin,⁵⁴ ether-linked lipids,⁵⁵ and PC lipids with polyunsaturated chains.⁵⁶ Here we report the SDP model (i.e., parsing scheme) for sphingomyelins (Fig. S2), which we used to determine the structure of fluid phase PSM and SSM through joint analysis of SANS and SAXS data combined with independently determined lipid volumes (Fig. S5). Complete results from the analysis are summarized in Table 1.

The structure of fluid phase sphingomyelin.

Structurally, sphingomyelin (SM) has the same choline headgroup as phosphatidylcholine (PC) lipids but possesses a sphingosine rather than a glycerol backbone. Both SM and PC lipids are present in the outer leaflet of mammalian plasma membranes in similar amounts.² While biologically relevant rafts are thought to be enriched in SM and cholesterol,⁴ in vitro studies of raft mixtures often use high-melting, fully saturated PC lipids (e.g., DPPC or DSPC) as stand-ins for sphingomyelin.^57–58 However, in raft-mimicking mixtures with the same low-melting lipid and cholesterol, there are reported differences between high-melting saturated PC lipids and sphingomyelins in their interactions with cholesterol,⁵⁹ ternary phase behavior,^60–61 and domain size.^61–62 It is therefore informative to compare the properties of the two lipid classes.

Figure 5 shows a comparison of the average chain length dependence of sphingomyelin structural parameters with those of various fully saturated or monounsaturated PC lipids¹⁷ with values either measured at, interpolated at, or (in the case of PSM) extrapolated to 60 °C, where all lipids are fluid phase. For all lipids, both the total volume and the bilayer thickness increase with increasing average chain length. This is also the case for PG¹⁸ and PE¹² lipids, suggesting that the increase in bilayer thickness upon addition of a CH₂ group is universal (that is, it does not depend on the lipid headgroup, or the nature of the chemical linkages in the backbone). In contrast to the thickness, the trend in A_L depends on chain saturation.

Figure 5. Comparison of structural parameters of PSM and SSM to phosphatidylcholine bilayers.

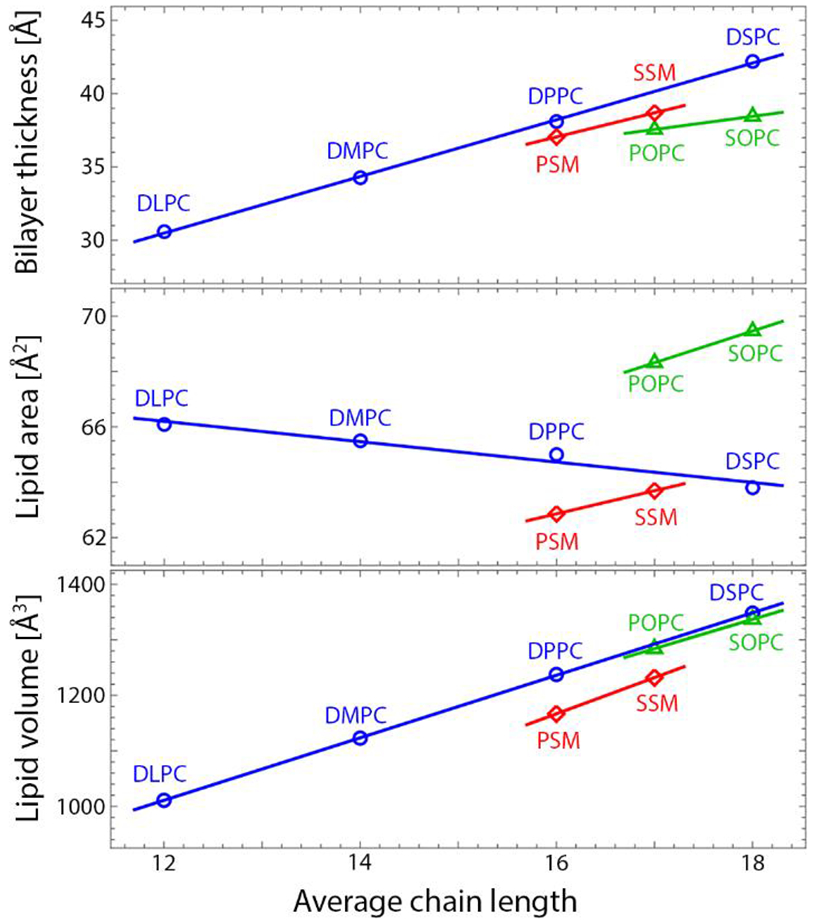
Shown are bilayer thickness (top), area per lipid (middle), and lipid volume (bottom) as a function of average chain length. The comparison is done at 60 °C; PSM is extrapolated and SSM is interpolated from values reported in Table 1. We estimate a 2% uncertainty for lipid area and bilayer thickness⁹ and 0.1% for lipid volumes.⁶⁷

A comparison of PSM and DPPC is instructive, as these lipids have the same average chain length and nearly identical main transition temperature. In particular, A_L is 3 Ų smaller for PSM compared to DPPC, suggesting that the sphingosine backbone is conducive to stronger lipid-lipid interactions (and hence, tighter packing) as was shown in a recent study.⁶³ For saturated PC lipids, decreased A_L with increasing chain length suggests that the largest contribution to lipid-lipid interactions is van der Waals attraction in the acyl chains; over a limited range, A_L decreases approximately linearly with increasing chain length. However, the introduction of a single cis double bond in the sn-2 chain of mixed-chain lipids (i.e., POPC and SOPC) reverses this trend: the addition of two CH₂ groups to the saturated sn-1 chain now causes an increase in A_L. Interestingly, a similar effect is observed for sphingomyelins upon increasing the length of the fully saturated N-acyl chain. For POPC and SOPC, the increase in A_L has been attributed to rotational isomerization counteracting the attractive van der Waals interactions.¹⁷ This is unlikely to be true for sphingomyelins: although they possess a double bond in their sphingosine chain, it is the trans isomer, it is located near the top of the chain, and it has an ordering rather than disordering effect on the lipid chains. Instead, the increase in A_L may be due to increasing interdigitation of the N-acyl chain with increasing length. Using X-ray diffraction, Maulik et al. reported A_L values of 47 Ų,⁶⁴ 55 Ų,⁶⁵ and 61.3 Å^{2 66} for PSM, SSM, and C24:0-SM, respectively. Although the first two values are much smaller than those reported here (a discrepancy that is discussed below), the trend of increasing A_L with increasing N-acyl chain length is similar to our observations for PSM and SSM. Those authors speculated that the trend may be due to the increasing length mismatch between the N-acyl and sphingosine chains. Interestingly, even though the sphingosine chain possesses 18 carbons, we find that in PSM simulations, the number density distribution of its terminal methyl carbon overlaps with the terminal methyl carbon of the 16-carbon N-acyl chain (Fig. S8). This suggests that due to the geometry of the sphingosine backbone, the sphingosine and N-acyl chain lengths are precisely matched for PSM. It is therefore reasonable that any further addition of carbons to the N-acyl chain will result in increased mismatch with the sphingosine chain. Although the SDP model combines the terminal methyls of the sphingosine and N-acyl chain into a single Gaussian distribution and therefore does not directly inform on interdigitation, it does report indirect effects such as increased A_L.

Comparison of area per lipid with literature values.

Experimentally determined bilayer structure plays a crucial role in the refinement and validation of MD force fields. Because it is directly related to bilayer thickness and indirectly related to many other bilayer properties including bending rigidity,⁶⁸ A_L often serves as a reference metric for the bilayer structure itself, and is the most frequently reported point of comparison between different experiments or between simulation and experiment.

Table 2 compares all literature reports (to our knowledge) of the major structural parameters for PSM and SSM at various temperatures determined from experiment or simulation. A few important points emerge from the data in Table 2. First, experimental reports of sphingomyelin structure are rather sparse. A recent study by Arsov et al.⁶⁹ analyzed PSM at 45 °C using diffuse low-angle X-ray scattering (LAXS), but the only other available scattering data for PSM and SSM is from X-ray diffraction (XRD) measurements of MLVs at 60 wt% water.^64–66 Second, a large discrepancy is observed in A_L obtained with XRD compared to LAXS or SAXS, with XRD values being much smaller both for PSM and SSM. For PSM in particular, the XRD value of 47 Ų suggests tight chain packing inconsistent with a fluid phase, and is indeed remarkably similar to values reported for saturated PC lipids in the gel phase.⁷⁰ Since A_L for PSM obtained from LAXS of oriented bilayer stacks is also much higher than the XRD result, curvature effects are unlikely to account for the observed inconsistency. We note that at 45 °C the PSM A_L obtained from LAXS (64 Ų) is also larger than the A_L we measured with SANS/SAXS (60 Ų). However, this difference is much smaller compared to the XRD values and can be explained in part by the different lipid volume used by Arsov et al., which accounts for about 1 Ų of the discrepancy.

Table 2.

Comparison of sphingomyelin structural parameters obtained from experiment and simulation.

Lipid	T [°C]	VL	AL	DB	DHH	Sample	Hydration	Technique	Reference
PSM	45	1151.6	60.0	38.4	38.9	LUV	full	SANS/SAXS	This work
		1171	64(2)	36.6	38	OMB	full*	Diffuse LAXS	69
	48		55.4		40.7	72 lipids		MD (CHARMM)	31
			56.5		39.6	288 lipids		MD (ANTON)	31
	50	1180(10)	52	45.4		128 lipids		MD (GROMACS)	71
		1168(12)	53.3(0.4)	43.8	43.7	200 lipids		MD (GROMACS)	72
		1126	54.1	41.6		128 lipids		MD (Slipids)	73
	55	1161.7	61.9	37.5	37.8	LUV	full	SANS/SAXS	This work
		1199	47	51	41	MLV	60%	XRD	64
SSM	45		54.5		43.0(0.1)	72 lipids		MD (CHARMM)	31
	50		55.4		42.7(0.1)	72 lipids		MD (CHARMM)	31
		1182	53	44.6	42.4	400 lipids		MD (GROMACS)	74
		1181	54.0	43.7		128 lipids		MD (Slipids)	73
	55	1226.8	62.5	39.3	40.0	LUV	full	SANS/SAXS	This work
		1232a	55	45	41	MLV	60%	XRD	65
	65	1237.1	64.9	38.1	39.4	LUV	full	SANS/SAXS	This work

^*Hydrated from vapor phase at 100% relative humidity

Owing to their biological relevance, sphingomyelins are frequently used in MD simulation studies.^31,71–75 Table 2 also shows that our experimentally determined A_L values for PSM and SSM are significantly larger than those obtained from MD simulations using the C36 CHARMM lipid force field for sphingolipids,³¹ which was modified specifically to obtain agreement with available ²H-NMR order parameter data.⁴³ Other force fields result in A_L values similar to, or even smaller than, those obtained with CHARMM36. We speculate on possible explanations for the seemingly contradictory structural information revealed by NMR and scattering techniques in the last section of the Discussion.

Effects of curvature on SM structure.

Different techniques used to study bilayer structure such as wide-angle X-ray diffraction,⁷⁶ small-angle X-ray and neutron scattering,^{77 2}H NMR,⁷⁸ and MD simulations,⁷⁹ differ not only in their methodological details and probed structural aspects of the membrane, but also in the nature of the sample being examined. For example: X-ray diffraction requires stacked bilayers (either oriented on a substrate or as MLVs); SAXS and SANS utilize unilamellar free-floating liposomes typically with a diameter of 50–150 nm; ²H NMR is usually obtained from micron-sized MLVs; and MD simulations are routinely performed on flat bilayer patches of at most a few hundred lipids. When comparing results from different techniques, the underlying assumption is that bilayer structure is not influenced by the size or geometry of the system. However, one fundamental difference between the samples is the varying extents of membrane curvature. Indeed, our ESR measurements were designed to directly probe the effect of curvature on the order parameter—and by extension, lipid packing—of PSM.

As shown in Fig. 4, we found that membrane order reported by two nitroxide probes clearly decreases with increasing curvature below the main transition temperature of PSM, but not above it. One potential explanation is the accumulated curvature frustration in vesicles of small diameter, causing bilayer stress and potential packing defects in the gel-like membrane environment. A bilayer in the gel state is much harder to compress and bend relative to the fluid state, making the effects of curvature frustration more pronounced. It is worth noting that a recent study showed a pre-transition for PSM at 24°C indicating the presence of a possible ripple phase between 24°C and the main transition at 41°C.⁶⁹ While our study was not designed to characterize the full thermotropic behavior of PSM, we cannot exclude the possibility of differential partitioning of the ESR probes in the ordered and disordered regions of a rippled bilayer. Similarly, we cannot claim with certainty that the probes are equally distributed in the two bilayer leaflets. It has been reported that in SUVs the two leaflets of the bilayer can have substantially different packing densities due to the high curvature,⁸⁰ accompanied by a potential asymmetric interleaflet lipid distribution when multiple lipid species are present.⁸¹ Since both ESR probes contain a bulky nitroxide attached to their chains, it is possible that they preferentially reside in one or the other leaflet when in smaller vesicles. However, that ESR order cannot distinguish between PSM vesicles of different curvature at temperatures above the main transition strongly suggests that curvature is not a likely effector of changes in bilayer structure in the fluid state. This conclusion is further supported by the best-fit A_L values implied by model-free comparisons of simulations with experimental SAXS data for PSM LUVs (Fig. 3b and Fig. 3d) and MLVs (Fig. S9), as well as the relative agreement in A_L obtained from LUVs in the current work and published data from flat bilayer stacks⁶⁹ (Table 2).

Fluid bilayer structure determination: small-angle scattering compared to NMR.

The accuracy of MD simulations depends to a large extent on the set of force field parameters that define the interaction and bond energies between the lipid (and water) atoms. The development of these parameter sets relies on quantum mechanical calculations and refinement based on robust comparisons with experimental data. The latest CHARMM36 parameters for sphingomyelin were validated against available NMR data,⁴³ and showed very good agreement in the order parameter profile of the N-linked chain of PSM obtained from simulation and experiment at 48 °C.³¹ However, as we report here, the same set of parameters fails to reproduce the lipid packing of PSM measured with SANS and SAXS at 55 °C. In particular, the average area per lipid in an unconstrained NPT simulation of PSM at 55 °C (56.2 Ų) is 10% lower than that obtained from analysis of the scattering data (61.9 Ų).

One potential argument for this discrepancy is the inability of the scattering analysis to produce a reliable packing density of the bilayer from the scattering form factors. As mentioned earlier, the analysis is based on a real space bilayer model whose parameters are adjusted in an iterative procedure by fitting the bilayer’s scattering profile to the raw SAXS/SANS data in Fourier space. Since theoretically multiple real space models can produce the same scattering form factor, how likely is it that the resulting parameters faithfully represent the bilayer structure? A few different facts argue against the validity of this concern. First, the SDP modeling approach combines multiple sources of information (i.e., SAXS, SANS, and volumetric measurements) to increase the robustness of the recovered structural parameters. This approach has been shown to yield reproducible results for a wide range of lipids. Second, a direct model-free comparison of PSM scattering form factors from simulations to the raw scattering data shows in an unbiased way that the best agreement between the two is precisely at the area per lipid obtained from the joint refinement of the experimental data (Fig. 3). For that constrained area simulation at 61.9 Ų, both the neutron (Fig. 3a) and X-ray (Fig. 3b) scattering form factors and all structural parameters are remarkably similar to the experimentally determined values (Table 1). This result supports the reliability of the scattering analysis and further confirms the deviation of the structure of the unconstrained simulated bilayer from that of the LUV membrane.

Having established the validity of the scattering results, we expected that the constrained-area bilayer at 61.9 Ų would also show best agreement with NMR data that we collected at the simulation temperature of 55 °C. Surprisingly however, the model-free comparison with the experimental order parameter profile implied best overall agreement with a constrained area simulation at 58 Ų (Fig. 3c and Fig. 3d). Interestingly, none of the simulations resulted in good agreement for all carbons along the N-acyl chain. Specifically, the order of the first few carbons on the N-linked chain matched those of the PSM lipids in the unconstrained simulation, while the order of the remaining carbons was almost identical to the 59 Ų constrained-area simulation (Fig. 3c). Still, the PSM order parameter profile from the unconstrained simulation at 55 °C shows a much better agreement with the NMR order parameter profiles that we obtained at 45 °C and 48 °C (Table S3). While this observation cannot explain the discrepancy with scattering results (since even at 45 °C the SDP analysis indicates an A_L of 60 Ų), it does call into question the reliability of temperature scaling in MD simulations of sphingomyelin. While the CHARMM36 force field has been shown to reliably capture the temperature dependence of hydrocarbons and a range of lipids,^67,82–84 sphingolipids may pose challenges because they have a higher melting temperature and are often close to the main phase transition.

Because the NMR experiments were performed with PSM-d₃₁, it is possible that the discrepancy with scattering data could be explained by a structural difference between the deuterated lipid and its protiated counterpart. Indeed, we observe a 4 °C lowering of the main transition temperature of PSM-d₃₁ determined from NMR (Fig. 2) compared to PSM measured with DSC (Fig. S5), implying that the deuterated bilayer is slightly more disordered at a given fluid phase temperature. However, a chi-square comparison of the simulations with the PSM-d₃₁ SANS data set yields a best match with the constrained-area simulations at 61 Ų (Fig. 3d), slightly smaller than the 61.9 Ų found in the joint analysis, but 3 Å larger than the 58 Ų implied by NMR data. This suggests that isotope effects cannot fully explain the discrepancy between scattering and NMR data. Similarly, as discussed above, the different degrees of curvature in the MLVs measured with NMR and the LUVs measured with SANS/SAXS is also unlikely to play a role at 55 °C where the bilayer is in the fluid state.

One major difference between the bilayer models probed with the different experimental techniques is the amount of water in the samples. While scattering is performed on liposomes in excess water, unlike in the present study NMR measurements on PSM-d₃₁ have often been performed at < 50 wt% water.^{43, 85} The XRD studies of Maulik et al. reported the effect of water content on the structural parameters of PSM⁶⁴ and SSM⁶⁵ using MLV preparations similar to those used in NMR experiments. Comparing the trends at hydration levels up to 60%, they observed a plateau of the fluid-phase lipid area and bilayer thickness at 20–35 wt% water. However, the resulting plateaued A_L is lower than the value we obtained from analysis of SANS and SAXS data (Table 2). Similarly, the PSM A_L from XRD on MLVs at 50 wt% water is much lower than that obtained either from SANS/SAXS or diffuse LAXS measurements (Table 2). Thus, while bilayer structure does not appear to change for > 40 wt% water, XRD and NMR both executed under the same sample conditions (i.e., MLVs at nominally 50 wt% water) produce structural parameters indicative of a substantially more ordered and tightly packed bilayer relative to results obtained from oriented bilayer stacks at full hydration⁶⁹ or unilamellar vesicles at 98 wt% water (this work). One possible explanation is the potential difficulty in controlling bilayer hydration during prolonged periods of time at an elevated temperature. NMR measurements take ~1 hour per sample with the sample often measured at multiple temperatures consecutively (for example, in our NMR experiments we measured the sample at 12 different consecutive temperatures) while XRD data collection in the 1990s could take many hours on a home source instrument. Even though the samples were placed in sealed capillaries, we speculate that water condensation on the capillary walls could lead to a lower effective water content of the MLVs and consequently tighter lipid packing.

CONCLUSION

We report the structural parameters of palmitoyl and stearoyl sphingomyelin bilayers in the fluid state obtained from joint analysis of small-angle neutron and X-ray scattering data, including the ever-important area per lipid that is directly related to bilayer thickness and indirectly related to other bilayer properties. The results comprise an important addition to the scarce literature on SM structure as they provide robustly determined parameters of bilayer structure in fully hydrated free-floating liposomes. We further report order parameters of the N-linked chain of PSM obtained with ²H NMR as well as experimentally measured lipid volumes for both PSM and SSM. Through the use of all-atom MD simulations, a clear discrepancy is observed between the lipid packing density measured with scattering and the lipid order parameter obtained from NMR. As these two techniques provide crucial structural information used for testing and validation of simulation force field parameters, we discuss possible sources of the differences between the experimentally determined bilayer structures and emphasize the importance of considering sample conditions when interpreting structural results and designing experiments.