Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jul 16;20(8):6148–6154. doi: 10.1021/acs.nanolett.0c02417

Detecting Chirality in Two-Terminal Electronic Nanodevices

Xu Yang 1,*, Caspar H van der Wal 1, Bart J van Wees 1
PMCID: PMC7458476  PMID: 32672980

Abstract

graphic file with name nl0c02417_0005.jpg

Central to spintronics is the interconversion between electronic charge and spin currents, and this can arise from the chirality-induced spin selectivity (CISS) effect. CISS is often studied as magnetoresistance (MR) in two-terminal (2T) electronic nanodevices containing a chiral (molecular) component and a ferromagnet. However, fundamental understanding of when and how this MR can occur is lacking. Here, we uncover an elementary mechanism that generates such an MR for nonlinear response. It requires energy-dependent transport and energy relaxation within the device. The sign of the MR depends on chirality, charge carrier type, and bias direction. Additionally, we reveal how CISS can be detected in the linear response regime in magnet-free 2T nanodevices, either by forming a chirality-based spin-valve using two or more chiral components or by Hanle spin precession in devices with a single chiral component. Our results provide operation principles and design guidelines for chirality-based spintronic nanodevices and technologies.

Keywords: spintronics, spin−charge conversion, chirality-induced spin selectivity, time-reversal symmetry, nonlinear response

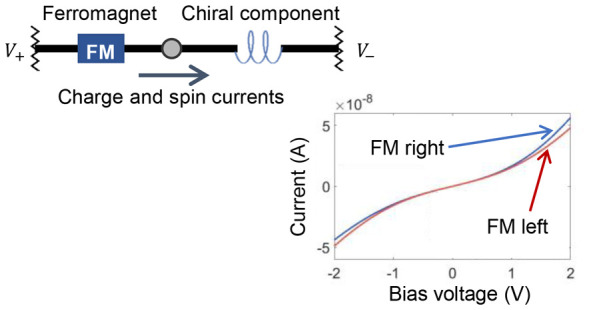
Recognizing and separating chiral enantiomers using electronic/spintronic technologies addresses fundamental questions of electronic charge and spin transport.1 It can open up new avenues for chiral chemistry and can bring chiral (molecular) structures into electronic and spintronic applications. This is enabled by the chirality-induced spin selectivity (CISS) effect,2−4 which describes the generation of a collinear spin current by a charge current through a chiral component (single molecule, assembly of molecules, or solid-state system). In two-terminal (2T) electronic nanodevices that contain a chiral component and a single ferromagnet (FM), CISS is reported as a change of electrical resistance upon magnetization reversal.5−12 This magnetoresistance (MR) has been interpreted in analogy to that of a conventional spin valve, based on the understanding that both the FM and the chiral component act as spin–charge converters.13−18 However, this interpretation overlooks the fundamental distinction between their underlying mechanisms—magnetism breaks time reversal symmetry, while CISS, as a spin–orbit effect, does not. In fact, Onsager reciprocity (which has its roots in fundamental microscopic reversibility) prohibits the detection of spin–orbit effects as 2T charge signals using a single FM in the linear response regime (at sufficiently low bias).19−22 Therefore, it requires theories beyond linear response for possible explanations of the MR observed in CISS experiments.22−25

Here we show that such a 2T MR can indeed arise from the breaking of Onsager reciprocity in the nonlinear regime. When the conditions for generating CISS in a chiral component are fulfilled, the emergence of the 2T MR requires two key ingredients: (a) energy-dependent electron transport due to, for instance, tunneling or thermally activated conduction through molecular orbitals, and (b) energy relaxation due to inelastic processes. Note that there exists an interesting parallel in chemistry, where absolute asymmetric synthesis is enabled by the lone influence of a magnetic field or magnetization in the nonlinear regime [see Supporting Information A (SI.A)].1,26,27

Below, before demonstrating the emergence of 2T MR in the nonlinear regime and identifying key factors that codetermine its sign, we will first introduce a transport matrix formalism unifying the description of coupled charge and spin transport in generic spin–charge converters such as a chiral component and an FM tunnel junction/interface (FMTJ). Afterward, we will explore new device designs that make 2T electrical detection of CISS possible in the linear response regime, and reveal a chiral spin valve built without magnetic materials.

Transport Matrix Formalism beyond Landauer Formula

The (spin-resolved) Landauer formula considers charge voltages as driving forces for electronic charge and spin transport.28 However, in a circuit with multiple spin–charge converters, we must also consider the buildup of spin accumulations, which also drive the coupled charge and spin transport (see SI.B).29,30 Here, we include this (thermodynamic) spin degree-of-freedom by extending the Landauer formula using a Büttiker-type multiterminal transmission analysis.31 Building on this, we introduce a transport matrix formalism that describes the (thermodynamic) responses of generic spin–charge converters. The symmetry/asymmetry of these transport matrices in the linear/nonlinear response regime is fundamentally related to the (breaking of) Onsager reciprocity. It does not depend on specific microscopic mechanisms and is not restricted to the transmission analysis that we use (see SI.B).

Spin–Charge Conversion in a Chiral Component

CISS arises from spin–orbit interaction and the absence of space-inversion symmetry. Further symmetry considerations require that the sign of the CISS-induced collinear spin currents must depend on the direction of the charge current and the (sign of) chirality. Note that the generation of CISS requires a nonunitary transport mechanism within the chiral component,32,33 which we assume to be present (see SI.C). In an ideal case, as illustrated in Figure 1, this directional, spin-dependent electron transport effectively allows only one spin orientation, say, parallel to the electron momentum, to transmit through the chiral component, and reflects and spin-flips the other.22 The spin-flip reflection prevents a net spin current in and out of electrodes at thermodynamic equilibrium.34

Figure 1.

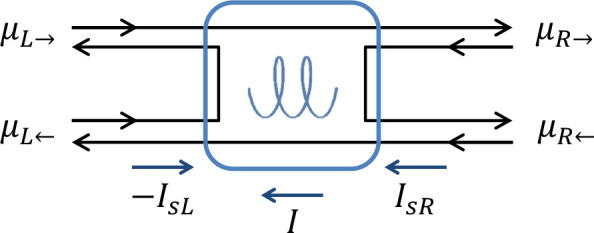
Figure 1

Open in a new tab

Illustration of CISS (ideal case). The directional electron transmission is spin-selective, and the unfavored spin is flipped and reflected. The chiral component is indicated by the blue helix and is assumed to favor the transmission of electrons with spin parallel to momentum. The electrons on both sides (L and R) of the chiral component are labeled with their spin-specific (→ or ←) electrochemical potentials μL(R)→(←). At thermodynamic equilibrium, any net charge or spin current in and out of electrodes is forbidden, but when biased, the chiral structure supports a charge current I and collinear spin currents on both sides IsL and IsR. The positive currents are defined as right-to-left, i.e. when the (spin-polarized) electrons flow from left to right.

We first describe the directional electron transmission (Inline graphic) and reflection (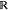Inline graphic) in a generalized chiral component using spin-space matrices introduced in ref (22). For right-moving (subscript ▷) electrons coming from the left-hand side of the component

graphic file with name nl0c02417_m003.jpg 1

where the matrix elements are probabilities of an electron being transmitted (t) or reflected (r) from an initial spin state (first subscript) to a final spin state (second subscript). For left-moving electrons, the corresponding matrices are the time-reversed forms of the above (see SI.D).

We extend the above coupled charge and spin transport by converting the spin-space matrices to transport matrices that link the thermodynamic drives and responses in terms of charge and spin. Following the symbols introduced in Figure 1, we define (charge) electrochemical potential μ = (μ→ + μ←)/2 and spin accumulation μs = (μ→ – μ←)/2, as well as charge current I = I→ + I← and spin current Is = I→ – I←. A subscript R or L is added when describing the quantities on a specific side of the component. With these, for a generalized case of Figure 1, we derive (see SI.D)

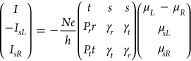graphic file with name nl0c02417_m004.jpg 2

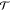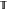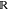where N is the number of (spin-degenerate) channels, e is elemental charge (positive value), and h is the Planck’s constant. An electrochemical potential difference μL – μR = −eV is provided by a bias voltage V. We name the 3 × 3 matrix the charge–spin transport matrix Inline graphic. All its elements are linear combinations of the spin-space Inline graphic and Inline graphic matrix elements and represent key transport properties of the chiral component. For example, t is the (averaged) transmission probability, r is the reflection probability (note that t + r = 2 because we have treated the two spins separately), Pt and Pr are the CISS-induced spin polarizations of the transmitted and reflected electrons, respectively, γt and γr describe spin relaxation and spin transport generated by spin accumulations, and s is the charge current generated by the spin accumulations due to the spin–charge conversion via CISS.

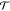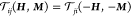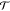We are particularly interested in the symmetry of Inline graphic. Equation 2 fully describes the coupled charge and collinear spin transport through a (nonmagnetic) chiral component, which is subject to Onsager reciprocity in the linear response regime. This requires Inline graphic, where H is the magnetic field and M is the magnetization.19 This then gives Ptt = Prr = s. In later discussions we will connect the R-side of the chiral component to an electrode (reservoir), where μsR = 0 and IsR is irrelevant. The Inline graphic matrix then reduces to a 2 × 2 form (see SI.D)

graphic file with name nl0c02417_m011.jpg 3

Note that t and γr do not depend on the (sign of) chirality, while Pt changes sign when the chirality is reversed.

Spin–Charge Conversion in an FMTJ

To calculate the coupled charge and spin transport in a generic 2T circuit where an (achiral) ferromagnet is also present, we need to derive a similar 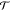Inline graphic matrix for an FMTJ. An FM breaks time-reversal symmetry and provides a spin-polarization PFM to any outflowing charge current. Based on this, we obtain for the R-side of the FMTJ (see SI.E)

graphic file with name nl0c02417_m013.jpg 4

where N′ is the number of (spin-degenerate) channels and T is the electron transmission probability accounting for both spins.

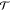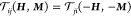The matrix Inline graphic here also satisfies the requirement Inline graphic, where a reversal of M corresponds to a sign change of PFM.

Origin of MR: Energy-Dependent Transport and Energy Relaxation

We model a generic 2T MR measurement geometry using Figure 2a. An FM and a chiral component are connected in series between two spin-unpolarized electrodes (L and R), and the difference between their electrochemical potentials μL – μR = −eV drives charge and spin transport. We introduce a node between the FM and the chiral component, which is characterized by an electrochemical potential μ and a spin accumulation μs. It preserves the spin but relaxes the energy of electrons to a Fermi–Dirac distribution due to inelastic processes (e.g. electron–phonon interaction). Physically, the node represents the effect of all inelastic processes that could happen during electron transport in actual nanodevices.

Figure 2.

Figure 2

Open in a new tab

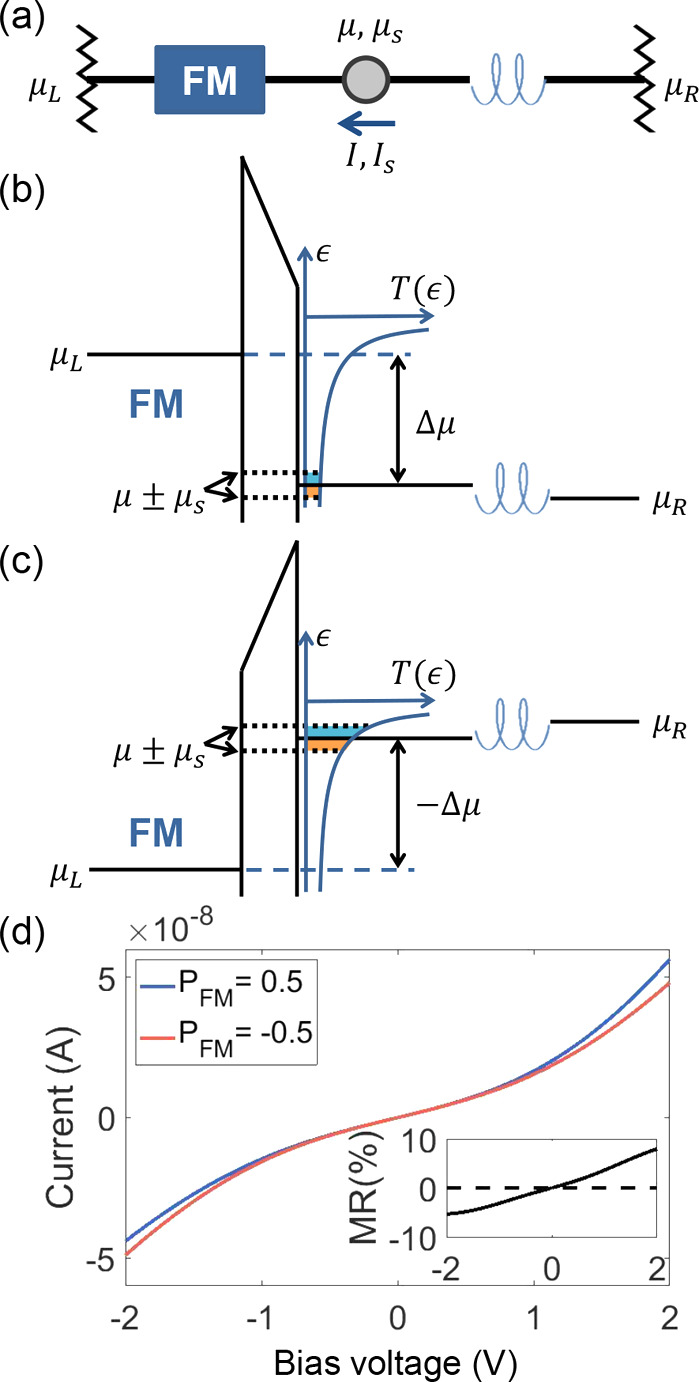
Origin of MR in a generic 2T circuit. (a). A 2T circuit containing an FM and a chiral component, connected by a node. The chiral component is assumed to favor the transmission of electrons with spin parallel to momentum. (b, c). Schematic energy diagrams of tunneling at the FMTJ under forward (b) and reverse (c) biases. The energy-dependent tunnel transmission T(ϵ) is sketched in blue, and the tunnel current affected by the spin accumulation μs is illustrated by the color-shaded areas (cyan and orange). (d). Example I–V curves considering the nonlinear mechanism of (b) and (c), while keeping the transmission through the chiral component constant (see SI.G). Note that positive bias voltage corresponds to the reverse bias scenario depicted in panel (c). The MR ratio, defined as (I+ – I–)/(I+ + I–), is plotted in inset. Here the subscript + or – denotes the corresponding sign of PFM, with PFM > 0 corresponding to a spin-right polarization for the injected electrons. The dashed line marks zero MR.

No MR in the Linear Response Regime

The 2T conductance G2T of this geometry in the linear response regime can be derived by applying a continuity condition in the node for both charge and spin currents, which gives (see SI.F)

graphic file with name nl0c02417_m016.jpg 5

It depends on the polarizations PFM and Pt only to second order, and does not depend on their product PFMPt. Therefore, the 2T conductance remains unchanged when the sign of PFM or Pt is reversed by magnetization or chirality reversal. This result confirms the vanishing MR in the linear response regime, as strictly required by Onsager reciprocity.22

This vanishing MR can be understood as a result of two simultaneous processes. First, by the conventional description, the charge current through the chiral component drives a collinear spin current and creates a spin accumulation in the node (spin injection by CISS), which is then detected as a charge voltage by the FM (spin detection by FM). This charge voltage indeed changes upon the FM magnetization reversal. However, this is always accompanied by the second process, where it is the FM that injects a spin current, and the Onsager reciprocal of CISS detects it as a charge voltage. This voltage also changes upon the FM magnetization reversal. In the linear regime, the two processes compensate each other, and the net result is a zero MR.

Emergence of MR in Nonlinear Regime and Its Sign

The key to inducing MR is to break the balance between the two processes, which can be done by using electrons at different energies for spin injection and spin detection. This requires the presence of energy relaxation inside the device, and it also needs the transport to be energy-dependent in at least one of the spin–charge converters. Note that the energy relaxation is crucial for generating MR, because Onsager reciprocity, which holds at each energy level, would otherwise prevent an MR even for nonlinear response despite the energy-dependent transport. We illustrate the emergence of MR using two examples of energy dependence, (a) quantum tunneling through the FMTJ and (b) thermally activated conduction through molecular orbitals. These two elementary examples reveal key factors that codetermine the sign of the nonlinear MR.

Example (a)

The asymmetric spin injection and detection in an FMTJ was previously discussed by Jansen et al. for an FM coupled to a semiconductor,35 and here we generalize it for our system. The energy diagrams for this tunneling process are sketched in Figure 2b and c for opposite biases. The bias opens up an energy window Δμ = μL – μ, and electrons within this window can contribute to the total tunnel current I. The energy distribution of these tunneling electrons follows the energy dependence of the tunnel transmission probability T(ϵ) (blue curve). Therefore, electrons that contribute the most to the tunnel current I are those at the highest available energy, which are at μL (in the FM) under forward bias, and are at the spin-split electrochemical potentials μ ± μs (in the node) under reverse bias.

The spin injection process concerns the spin current Is induced by the total charge current I through the FMTJ with spin polarization PFM (assuming energy-independent PFM). It is determined by the energy integral of T(ϵ) over the entire bias-induced window Δμ and is symmetric for opposite biases (assuming μs ≪ Δμ). In contrast, the spin detection process, which concerns the spin accumulation μs in the node at its highest energy μ (Fermi level), is not symmetric for opposite biases. Effectively, the spin accumulation describes the deficit of one spin and the surplus of the other, as illustrated by the orange- and blue-shaded regions under the T(ϵ) curve in Figure 2b and c, and therefore drives an (additional) charge current proportional to the area difference between the two regions. This detected charge current depends on the transmission probability at energy μ and increases monotonically as the bias becomes more reverse.

The different bias dependences for spin injection and detection break Onsager reciprocity for nonlinear response. This is also shown by the different off-diagonal terms in the nonlinear transport equation (see SI.G)

graphic file with name nl0c02417_m017.jpg 6

where 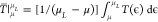Inline graphic is the averaged transmission over the energy window Δμ = μL – μ, and T|ϵ=μ is the transmission evaluated at the Fermi level of the node ϵ = μ. In the linear response regime, when μL ≈ μ, this equation returns to eq 4.

The tunnel I–V and the MR due to this mechanism are illustrated in Figure 2d using realistic circuit parameters (see SI.I). The MR ratio reaches nearly 10% at large biases, but strictly vanishes at zero bias. Notably, the MR is positive under positive bias voltage (corresponds to reverse bias as in Figure 2c), and it reverses sign as the bias changes sign.

Example (b)

The nonreciprocal spin injection and detection can also arise from the nonlinear transport through the chiral component. In principle, this could also be due to tunneling, but we focus here on another aspect, the Fermi–Dirac distribution of electrons. This is negligible when the transmission function T(ϵ) is smooth, as for the case of tunneling (thus we have assumed zero temperature for deriving eq 6), but it becomes dominant when electron (or hole) transmission is only allowed at certain discrete energy levels or energy bands that are away from Fermi level, as for the case of conduction through molecular orbitals or through energy bands in semiconductors. We illustrate this in Figure 3a considering the resonant transmission through the LUMO (lowest unoccupied molecular orbital) and the HOMO (highest occupied molecular orbital) of a chiral molecule (see SI.H). For spin injection, the generated spin current is proportional to the total charge current, which depends on the (bias-induced) electrochemical potential difference between the node and the right electrode, and is symmetric for opposite biases. In comparison, for spin detection, the spin-split electrochemical potentials in the node μ ± μs induce unequal occupations of opposite spins at each MO (depending on the MO position with respect to the node Fermi level μ), and it is not symmetric for opposite biases. This different bias dependence breaks Onsager reciprocity for nonlinear response and gives rise to MR.

Figure 3.

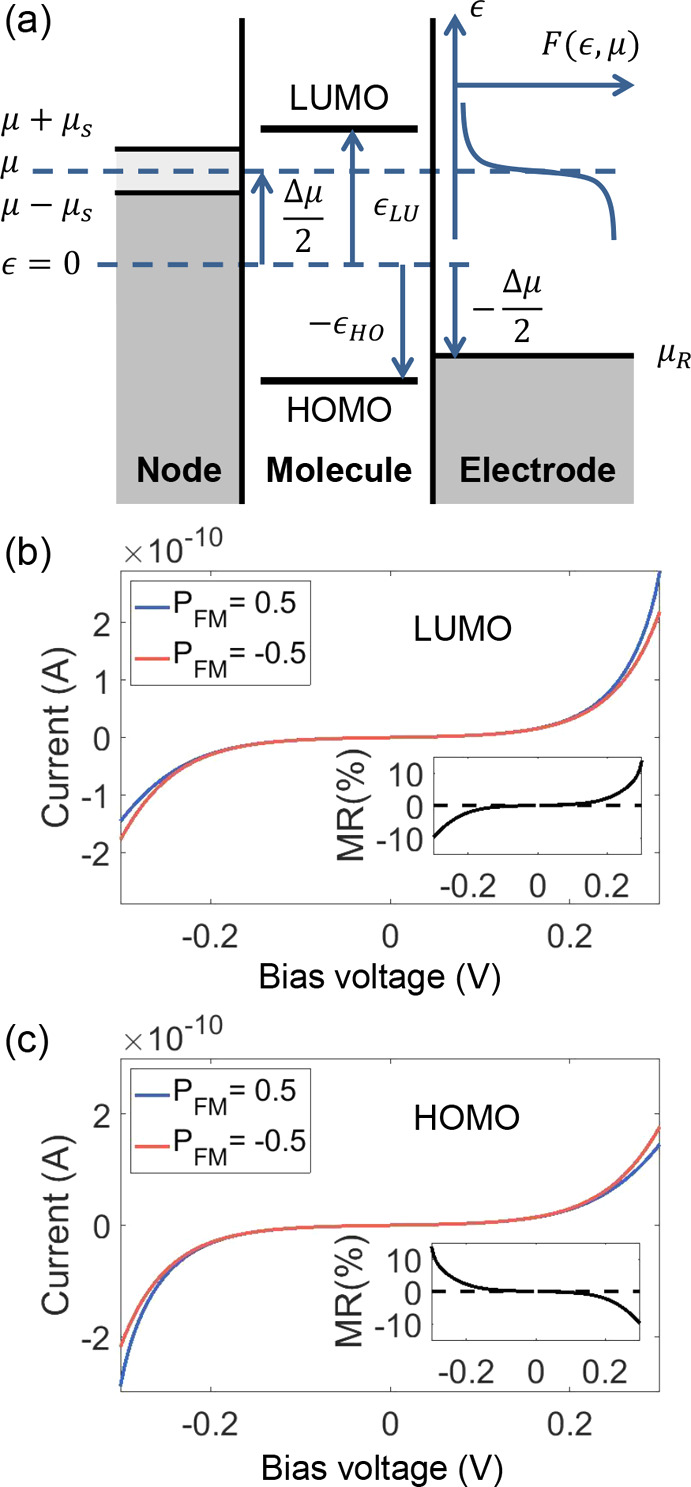
Figure 3

Open in a new tab

Generating MR by thermally activated conduction through molecular orbitals. (a) Schematic energy diagram of resonant transmission through molecular orbitals in a chiral component (molecule). The LUMO and HOMO levels and the bias-dependent electrochemical potentials are labeled, and the energy- and bias-dependent Fermi–Dirac function F(ϵ,μ) is sketched in blue. (b and c) Example I–V curves and MR (inset) due to the resonant transmission through the LUMO (b) and the HOMO (c), for the same device geometry as in Figure 2a but with the transmission of the FMTJ set constant. The chiral molecule is assumed to favor the transmission of electrons with spin parallel to momentum.

We consider the transmission through either only the LUMO or only the HOMO, and their example I–V curves and MR ratios are plotted in Figure 3b–c, respectively (see SI.I). The MR is able to reach tens of percent even at relatively small biases, and changes sign as the bias reverses. Remarkably, the bias dependence of the MR is opposite for LUMO and HOMO, implying that the charge carrier type, i.e. electrons or holes, codetermines the sign of the MR. Again, the MR strictly vanishes as the bias returns to zero (linear response regime). An overview of the sign of MR is given in SI.J.

Chiral Spin Valve

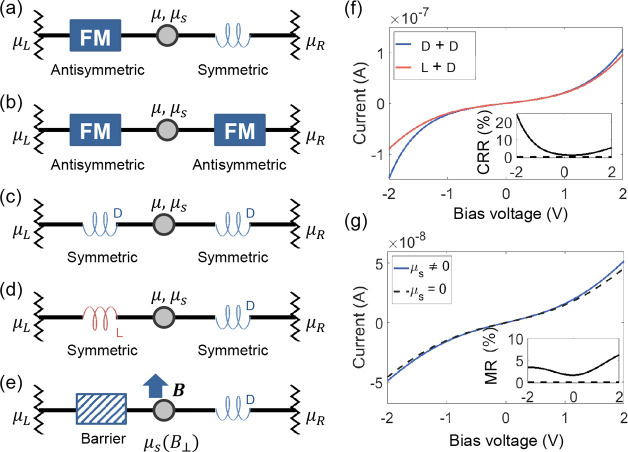
In the linear response regime, our formalism uses an antisymmetric transport matrix (opposite off-diagonal terms) to describe the coupled charge and spin transport through the FMTJ and uses a symmetric one for the chiral component. The symmetries of these transport matrices are directly required by Onsager reciprocity and have consequences when considering 2T circuits containing two generic spin–charge converting components, as illustrated in Figure 4. If the two components are described by transport matrices with opposite symmetries, a 2T MR signal is forbidden in the linear response regime (Figure 4a). This restriction is lifted if both components are described by matrices with the same symmetry. For example, in a conventional spin valve (Figure 4b), the two FMs are both described by antisymmetric transport matrices, and the magnetization reversal of one FM indeed changes the 2T conductance even in the linear response regime.

Figure 4.

Figure 4

Open in a new tab

Generic 2T spin-valve device geometries with the symmetry of the charge–spin transport matrix labeled for each component. (a) The aforementioned FM–chiral geometry where MR signals are strictly forbidden in the linear response regime. (b) An FM–FM geometry, as in a conventional spin valve, where MR signals are allowed in the linear response regime. (c, d) A chiral–chiral geometry for using the same (c) and opposite (d) chiralities, as marked by color and labeled with d or l (here we assume the d-chiral component favors the transmission of electrons with spin parallel to momentum, and the l-chiral component favors the antiparallel ones). The spin-valve effect can be achieved, even in the linear response regime, by reversing the chirality of one component. (e) Geometry for directly probing the spin accumulation generated by a single chiral component, which is connected to a nonmagnetic barrier via a node. A perpendicular magnetic field B suppresses spin accumulation in the node via Hanle spin precession. (f) Example I–V curves for a chiral−chiral spin valve, with the two curves representing the geometries in panel (c) and (d), respectively. The corresponding chirality-reversal resistance (CRR) ratio, as defined by CRR = (Idd – Ild)/(Idd + Ild) (the two subscripts refer to the chiralities of the two chiral components), is plotted in the inset. (g) Example I–V for the geometry in panel (e), calculated for cases with μs either fully or not-at-all suppressed by Hanle precession. The corresponding MR is shown in inset, which is defined as the difference of the two curves divided by their sum.

A less obvious outcome of this symmetry consideration is that a combination of two chiral components (both described by symmetric matrices) can also form a spin valve, provided that at least one of them can reverse chirality, like a molecular rotor.36 This is illustrated in Figure 4c–d, with example I–V curves in Figure 4f. In the linear response regime, this geometry already produces a nonzero chirality-reversal resistance (CRR, see figure caption for definition) signal, which is further enhanced to tens of percent as the bias increases.

Finally, we introduce a 2T geometry that can detect the spin–charge conversion due to a single chiral component, as shown in Figure 4e. Here, a charge current through the chiral component can create a spin accumulation in the node (even in the linear response regime), which can then be suppressed using a perpendicular magnetic field due to Hanle spin precession. This results in a magnetic-field-dependent 2T conductance, and Figure 4g shows the I–V curves for zero magnetic field (blue solid curve) and for when the field fully suppresses the spin accumulation (black dashed curve). The corresponding MR (inset) is nonzero even in the linear response regime and can be enhanced by increasing bias.

Discussion

We explained that energy-dependent transport combined with energy relaxation can give rise to MR signals in 2T electronic nanodevices containing an FM and a chiral component. We analyzed the (sign of) MR using two elementary examples: energy-dependent tunneling through FMTJ (plus a chiral component at linear response) and energy-dependent Fermi–Dirac distribution for thermally activated resonant transmission through the chiral component (plus an FMTJ at linear response). Here, we note that other mechanisms such as electron–electron interaction may also play a role in electron transport through chiral molecules.37,38 This however does not affect our (qualitative) conclusions regarding the onset and the sign of MR, and can be quantitatively accounted for by deriving the transport matrix of the chiral component accordingly39,40 (see SI.K).

We also assumed that the overall conduction through the circuit components is (phase) incoherent. In practice, coherent conduction mechanisms, such as direct tunneling from the FM into an MO of the chiral molecule, may also be present. For fully incoherent conduction, the chirality-based spin valve (Figure 4c–d) resembles a conventional CPP GMR device,41 while if coherent tunneling dominates, it is comparable to a TMR device.42

Finally, we draw attention to the sign of the nonlinear MR, which depends on the dominating nonlinear element, the bias direction, the charge carrier type, and the (sign of) chirality, as summarized in SI.J. We plotted the MR as a function of bias while assuming the chirality and the charge carrier type remain unchanged. However, in experimental conditions, it is possible that the charge carrier type switches when the bias is reversed, and consequently the MR can have the same sign for opposite biases. Such a bias-even MR is indeed in agreement with most experimental observations.5,6,8−12 The experimental conditions concerning the vanishing MR in the linear response regime are however unclear, since sometimes the currents are too low to be measured.5,6,9 For experiments where a linear response regime can be identified, some do show a strongly suppressed or vanishing MR,8,12 while some do not.10,11 This inconsistency thus requires further investigation.

Acknowledgments

This work is supported by the Zernike Institute for Advanced Materials (ZIAM), and the Spinoza prize awarded to Professor B. J. van Wees by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO). The authors acknowledge discussions with R. Naaman, C. Herrmann, A. Aharony, and G. E. W. Bauer.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c02417.

  • Further discussion and/or derivation of the following: (A) Comparison to absolute asymmetric (chemical) synthesis; (B) Beyond the Landauer formula; (C) Nonunitarity for generating CISS and energy relaxation for generating MR; (D) Spin and charge transport in a nonmagnetic chiral component; (E) Spin and charge transport at an achiral ferromagnetic tunnel junction/interface; (F) Spin and charge transport in a generic 2T circuit; (G) Reciprocity breaking by energy-dependent tunneling; (H) Reciprocity breaking by thermally activated resonant transmission through molecular orbitals; (I) Parameters for example I–V curves; (J) Sign of the nonlinear 2T MR; and (K) Beyond noninteracting-electron picture. (PDF)

The authors declare no competing financial interest.

Supplementary Material

nl0c02417_si_001.pdf (679.9KB, pdf)

References

  1. Barron L. D. True and false chirality and absolute asymmetric synthesis. J. Am. Chem. Soc. 1986, 108, 5539–5542. 10.1021/ja00278a029. [DOI] [Google Scholar]
  2. Naaman R.; Paltiel Y.; Waldeck D. H. Chiral molecules and the electron spin. Nature Reviews Chemistry 2019, 3, 250–260. 10.1038/s41570-019-0087-1. [DOI] [Google Scholar]
  3. Göhler B.; Hamelbeck V.; Markus T. Z.; Kettner M.; Hanne G. F.; Vager Z.; Naaman R.; Zacharias H. Spin selectivity in electron transmission through self-assembled monolayers of double-stranded DNA. Science 2011, 331, 894–897. 10.1126/science.1199339. [DOI] [PubMed] [Google Scholar]
  4. Inui A.; Aoki R.; Nishiue Y.; Shiota K.; Kousaka Y.; Shishido H.; Hirobe D.; Suda M.; Ohe J.-i.; Kishine J.-i.; et al. Chirality-Induced Spin-Polarized State of a Chiral Crystal CrNb3S6. Phys. Rev. Lett. 2020, 124, 166602. 10.1103/PhysRevLett.124.166602. [DOI] [PubMed] [Google Scholar]
  5. Suda M.; Thathong Y.; Promarak V.; Kojima H.; Nakamura M.; Shiraogawa T.; Ehara M.; Yamamoto H. M. Light-driven molecular switch for reconfigurable spin filters. Nat. Commun. 2019, 10, 2455. 10.1038/s41467-019-10423-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Lu H.; Wang J.; Xiao C.; Pan X.; Chen X.; Brunecky R.; Berry J. J.; Zhu K.; Beard M. C.; Vardeny Z. V. Spin-dependent charge transport through 2D chiral hybrid lead-iodide perovskites. Science Advances 2019, 5, eaay0571 10.1126/sciadv.aay0571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Aragonès A. C.; Medina E.; Ferrer-Huerta M.; Gimeno N.; Teixidó M.; Palma J. L.; Tao N.; Ugalde J. M.; Giralt E.; Díez-Pérez I.; et al. Measuring the Spin-Polarization Power of a Single Chiral Molecule. Small 2017, 13, 1602519. 10.1002/smll.201602519. [DOI] [PubMed] [Google Scholar]
  8. Kiran V.; Mathew S. P.; Cohen S. R.; Hernández Delgado I.; Lacour J.; Naaman R. Helicenes—A new class of organic spin filter. Adv. Mater. 2016, 28, 1957–1962. 10.1002/adma.201504725. [DOI] [PubMed] [Google Scholar]
  9. Xie Z.; Markus T. Z.; Cohen S. R.; Vager Z.; Gutierrez R.; Naaman R. Spin specific electron conduction through DNA oligomers. Nano Lett. 2011, 11, 4652–4655. 10.1021/nl2021637. [DOI] [PubMed] [Google Scholar]
  10. Torres-Cavanillas R.; Escorcia-Ariza G.; Mondal P. C.; Rosaleny L. E.; Giménez-Santamarina S.; Brotons I.; Sessolo M.; Galbiati M.; Tatay S.; Gaita-Ariño A.. et al. Room temperature spin filtering in chiral metallopeptides. 2019, 1905.09225, arXiv. https://arxiv.org/abs/1905.09225 (accessed July 16, 2020).
  11. Liu T.; Wang X.; Wang H.; Shi G.; Gao F.; Feng H.; Deng H.; Hu L.; Lochner E.; Schlottmann P.. et al. Spin selectivity through chiral polyalanine monolayers on semiconductors. 2019. 2001.00097. arXiv. https://arxiv.org/abs/2001.00097 (accessed July 16, 2020).
  12. Kulkarni C.; Mondal A. K.; Das T. K.; Grinbom G.; Tassinari F.; Mabesoone M. F.; Meijer E.; Naaman R. Highly Efficient and Tunable Filtering of Electrons’ Spin by Supramolecular Chirality of Nanofiber-Based Materials. Adv. Mater. 2020, 32, 1904965. 10.1002/adma.201904965. [DOI] [PubMed] [Google Scholar]
  13. Michaeli K.; Naaman R. Origin of Spin-Dependent Tunneling Through Chiral Molecules. J. Phys. Chem. C 2019, 123, 17043–17048. 10.1021/acs.jpcc.9b05020. [DOI] [Google Scholar]
  14. Medina E.; González-Arraga L. A.; Finkelstein-Shapiro D.; Berche B.; Mujica V. Continuum model for chiral induced spin selectivity in helical molecules. J. Chem. Phys. 2015, 142, 194308. 10.1063/1.4921310. [DOI] [PubMed] [Google Scholar]
  15. Guo A.-M.; Sun Q.-F. Spin-selective transport of electrons in DNA double helix. Phys. Rev. Lett. 2012, 108, 218102. 10.1103/PhysRevLett.108.218102. [DOI] [PubMed] [Google Scholar]
  16. Zöllner M. S.; Varela S.; Medina E.; Mujica V.; Herrmann C. Insight into the origin of Chiral-Induced Spin Selectivity from a Symmetry Analysis of Electronic Transmission. J. Chem. Theory Comput. 2020, 16, 2914–2929. 10.1021/acs.jctc.9b01078. [DOI] [PubMed] [Google Scholar]
  17. Díaz E.; Domínguez-Adame F.; Gutierrez R.; Cuniberti G.; Mujica V. Thermal Decoherence and Disorder Effects on Chiral-Induced Spin Selectivity. J. Phys. Chem. Lett. 2018, 9, 5753–5758. 10.1021/acs.jpclett.8b02196. [DOI] [PubMed] [Google Scholar]
  18. Geyer M.; Gutierrez R.; Mujica V.; Cuniberti G. Chirality-Induced Spin Selectivity in a Coarse-Grained Tight-Binding Model for Helicene. J. Phys. Chem. C 2019, 123, 27230–27241. 10.1021/acs.jpcc.9b07764. [DOI] [Google Scholar]
  19. Onsager L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405. 10.1103/PhysRev.37.405. [DOI] [Google Scholar]
  20. Büttiker M. Symmetry of electrical conduction. IBM J. Res. Dev. 1988, 32, 317–334. 10.1147/rd.323.0317. [DOI] [Google Scholar]
  21. Adagideli I.; Bauer G. E. W.; Halperin B. I. Detection of current-induced spins by ferromagnetic contacts. Phys. Rev. Lett. 2006, 97, 256601. 10.1103/PhysRevLett.97.256601. [DOI] [PubMed] [Google Scholar]
  22. Yang X.; van der Wal C. H.; van Wees B. J. Spin-dependent electron transmission model for chiral molecules in mesoscopic devices. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99, 024418 10.1103/PhysRevB.99.024418. [DOI] [Google Scholar]
  23. Dalum S.; Hedegård P. Theory of Chiral Induced Spin Selectivity. Nano Lett. 2019, 19, 5253–5259. 10.1021/acs.nanolett.9b01707. [DOI] [PubMed] [Google Scholar]
  24. Naaman R.; Waldeck D. H. Comment on “Spin-dependent electron transmission model for chiral molecules in mesoscopic devices. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101, 026403 10.1103/PhysRevB.101.026403. [DOI] [Google Scholar]
  25. Yang X.; van der Wal C. H.; van Wees B. J. Reply to “Comment on Spin-dependent electron transmission model for chiral molecules in mesoscopic devices. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101, 026404 10.1103/PhysRevB.101.026404. [DOI] [Google Scholar]
  26. Micali N.; Engelkamp H.; van Rhee P. G.; Christianen P. C. M.; Scolaro L. M.; Maan J. C. Selection of supramolecular chirality by application of rotational and magnetic forces. Nat. Chem. 2012, 4, 201–207. 10.1038/nchem.1264. [DOI] [PubMed] [Google Scholar]
  27. Banerjee-Ghosh K.; Dor O. B.; Tassinari F.; Capua E.; Yochelis S.; Capua A.; Yang S.-H.; Parkin S. S.; Sarkar S.; Kronik L.; et al. Separation of enantiomers by their enantiospecific interaction with achiral magnetic substrates. Science 2018, 360, 1331–1334. 10.1126/science.aar4265. [DOI] [PubMed] [Google Scholar]
  28. Büttiker M.; Imry Y.; Landauer R.; Pinhas S. Generalized many-channel conductance formula with application to small rings. Phys. Rev. B: Condens. Matter Mater. Phys. 1985, 31, 6207. 10.1103/PhysRevB.31.6207. [DOI] [PubMed] [Google Scholar]
  29. Brataas A.; Nazarov Y. V.; Bauer G. E. W. Finite-element theory of transport in ferromagnet–normal metal systems. Phys. Rev. Lett. 2000, 84, 2481. 10.1103/PhysRevLett.84.2481. [DOI] [PubMed] [Google Scholar]
  30. Shekhter R.; Entin-Wohlman O.; Aharony A. Mechanically controlled spin-selective transport. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 045401 10.1103/PhysRevB.90.045401. [DOI] [Google Scholar]
  31. Büttiker M. Four-terminal phase-coherent conductance. Phys. Rev. Lett. 1986, 57, 1761. 10.1103/PhysRevLett.57.1761. [DOI] [PubMed] [Google Scholar]
  32. Bardarson J. H. A proof of the Kramers degeneracy of transmission eigenvalues from antisymmetry of the scattering matrix. J. Phys. A: Math. Theor. 2008, 41, 405203. 10.1088/1751-8113/41/40/405203. [DOI] [Google Scholar]
  33. Matityahu S.; Utsumi Y.; Aharony A.; Entin-Wohlman O.; Balseiro C. A. Spin-dependent transport through a chiral molecule in the presence of spin-orbit interaction and nonunitary effects. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 075407 10.1103/PhysRevB.93.075407. [DOI] [Google Scholar]
  34. Kiselev A. A.; Kim K. W. Prohibition of equilibrium spin currents in multiterminal ballistic devices. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 153315. 10.1103/PhysRevB.71.153315. [DOI] [Google Scholar]
  35. Jansen R.; Spiesser A.; Saito H.; Fujita Y.; Yamada S.; Hamaya K.; Yuasa S. Nonlinear Electrical Spin Conversion in a Biased Ferromagnetic Tunnel Contact. Phys. Rev. Appl. 2018, 10, 064050 10.1103/PhysRevApplied.10.064050. [DOI] [Google Scholar]
  36. Koumura N.; Zijlstra R. W.; van Delden R. A.; Harada N.; Feringa B. L. Light-driven monodirectional molecular rotor. Nature 1999, 401, 152–155. 10.1038/43646. [DOI] [PubMed] [Google Scholar]
  37. Díaz E.; Contreras A.; Hernández J.; Domínguez-Adame F. Effective nonlinear model for electron transport in deformable helical molecules. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2018, 98, 052221 10.1103/PhysRevE.98.052221. [DOI] [Google Scholar]
  38. Fransson J. Chirality-Induced Spin Selectivity: The Role of Electron Correlations. J. Phys. Chem. Lett. 2019, 10, 7126–7132. 10.1021/acs.jpclett.9b02929. [DOI] [PubMed] [Google Scholar]
  39. Brandbyge M.; Mozos J.-L.; Ordejón P.; Taylor J.; Stokbro K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 65, 165401. 10.1103/PhysRevB.65.165401. [DOI] [Google Scholar]
  40. Meir Y.; Wingreen N. S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 1992, 68, 2512. 10.1103/PhysRevLett.68.2512. [DOI] [PubMed] [Google Scholar]
  41. Baibich M. N.; Broto J. M.; Fert A.; Van Dau F. N.; Petroff F.; Etienne P.; Creuzet G.; Friederich A.; Chazelas J. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472. 10.1103/PhysRevLett.61.2472. [DOI] [PubMed] [Google Scholar]
  42. Moodera J. S.; Kinder L. R.; Wong T. M.; Meservey R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 1995, 74, 3273. 10.1103/PhysRevLett.74.3273. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c02417_si_001.pdf (679.9KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES