Unsupervised dimensionality reduction for exposome research

Abstract

Understanding the effect of the environment on human health has benefited from progress made in measuring the exposome. High resolution mass spectrometry (HRMS) has made it possible to measure small molecules across a large dynamic range, allowing researchers to study the role of low abundance environmental toxicants in causing human disease. HRMS data have a high dimensional structure (number of predictors >> number of observations), generating information on the abundance of many chemical features (predictors) which may be highly correlated. Unsupervised dimension reduction techniques can allow dimensionality reduction of the various features into components that capture the essence of the variability in the exposome dataset. We illustrate and discuss the relevance of three different unsupervised dimension reduction techniques: principal component analysis, factor analysis, and non-negative matrix factorization. We focus on the utility of each method in understanding the relationship between the exposome and a disease outcome and describe their strengths and limitations. While the utility of these methods is context specific, it remains important to focus on the interpretability of results from each method.

Environmental determinants of health are receiving increased attention since genome and inheritance studies have revealed that genetic variation only explains about 20% of human disease risk [1,2]. There are various environmental factors that affect human health, including environmental chemicals, dietary factors, lifestyle, the built environment, exposure to microbes, as well as structural policies that influence healthcare and healthy behaviors. To this effect, many studies have evaluated the effect of single or a small number of exposures in isolation on various health outcomes. However, environmental exposures rarely happen in isolation and are accompanied with other exposures and context-specific factors. Along with the complexity of co-exposures, humans are constantly interacting with their environment over their life course, and exposures are spatiotemporally dynamic. The exposome concept emerged from this realization. In 2005, Christopher Wild formally coined the term and defined it as the “life-course environmental exposures (including lifestyle factors), from the prenatal period onwards” [3]. This definition has been modified over the last 15 years, but most revisions agree that the exposome comprises the entire set of lifelong environmental exposures and their associated biological response [1,2,4–6].

Measuring the exposome has benefited from technological advances in mass spectrometers. The arrival of high-resolution mass spectrometers (HRMS) has made it possible to measure small molecules (85–1250 Da) in a biological matrix with a large dynamic range, facilitating measurement of small molecules arising from endogenous metabolism—which are usually highly abundant (milli to picomoles)—and small molecules from exogenous sources that have a lower abundance in biological matrices (nano to picomoles) [7]. In this paper, we define the exposome as the sum of environmental exposures and the biological response induced by these environmental exposures. This definition assumes that meaningful environmental exposures that affect human health will produce a biological response which will be reflected in alterations to endogenous metabolic processes. Thus, measurements of small molecules in a biological matrix will allow us to measure this exposomic profile and assess biochemical changes that accompany exposure on a systems level. Using techniques from metabolomics, we can understand the biological effect associated with the exposome. For example, Walker et al. measured the exposomic profile of trichloroethylene (TCE) exposure among factory workers and found chlorinated metabolites in the plasma of factory workers that were correlated with markers of immune and kidney function along different parts of the pathway of TCE toxicity [8]. HRMS can also be leveraged to measure the sum of environmental chemicals in a matrix. By coupling gas chromatography to an HRMS, researchers have measured numerous chemicals of interest in a single sample simultaneously, e.g., the US Environmental Protection Agency’s ring trial, wrist band studies, etc. [9,10].

Exposomic data from HRMS are high-dimensional and complex. When untargeted methods are used to characterize the exposome, the number of chemical signals can be greater than 100,000 [11]. These data tables represent the primary input for bioinformatic and biostatistical analysis to evaluate biological meaning and to determine exogenously derived chemicals that may be of relevance to an outcome of interest. Since detected analytes are not annotated a priori, the results from HRMS contain information on each detected ion (a feature). Each feature is characterized by its mass-to-charge ratio, the retention time at which the compound eluted from the chromatographic column, and its abundance in the sample. Some features may arise from the same parent compound but during ionization may lead to formation of multiple ions with different masses with the same retention times. Therefore, the feature table may contain degenerate features which will be highly correlated since they arise from the same parent compound. Thus, correlation is present not only due to exposure sources and biological processes, but also arises from the analysis itself [12]. This forces researchers to deal with the “curse of dimensionality” and to capture the essence of the data generated [13]. Given the high correlations across chemical exposures, single chemical association studies are not appropriate, with implications for health that are missed using a “candidate” approach. Furthermore, high correlation compounds correction for multiple testing, decreasing study power and inflating the potential for false negatives.

Data dimensionality reduction approaches produce a manageable number of variables, allow for better visualization, remove redundant and uninformative variables, and reduce computational burden [14]. Several techniques have been described that reduce the size of the data table while minimizing loss of information, describing the essence of the data generated. These include unsupervised and supervised methods. In supervised methods, the outcome of interest informs the dimensionality reduction solution. These methods are used for feature selection and include—but are not limited to—different forms of penalized regression: least absolute shrinkage and selection operator (LASSO) [15], ridge regression [16], and elastic net regression [17], and different modifications of partial least squares regression [18,19]. Unsupervised methods do not take the outcome of interest under consideration during feature extraction. The goal in unsupervised dimensionality reduction is to discover the underlying structure in the data. These methods are tuned for pattern recognition that can aid in data visualization, data exploration, and uncovering latent variables. A popular method for unsupervised linear transformation of data is principal components analysis. Different unsupervised methods also exist for non-linear data transformations [20] like the kernel PCA [21], isomap [22] and autoencoders [23]. In this paper, we focus on unsupervised methods aiming to reduce the number of variables under study and obtain a smaller set of principal variables through feature extraction. We focus on the use of three methods for exposome research: factor analysis (FA), principal components analysis (PCA), and non-negative matrix factorization (NMF) (Figure 1). While NMF and FA have not yet been widely used with high-resolution mass spectrometry data, we think they offer useful applications.

Figure 1.

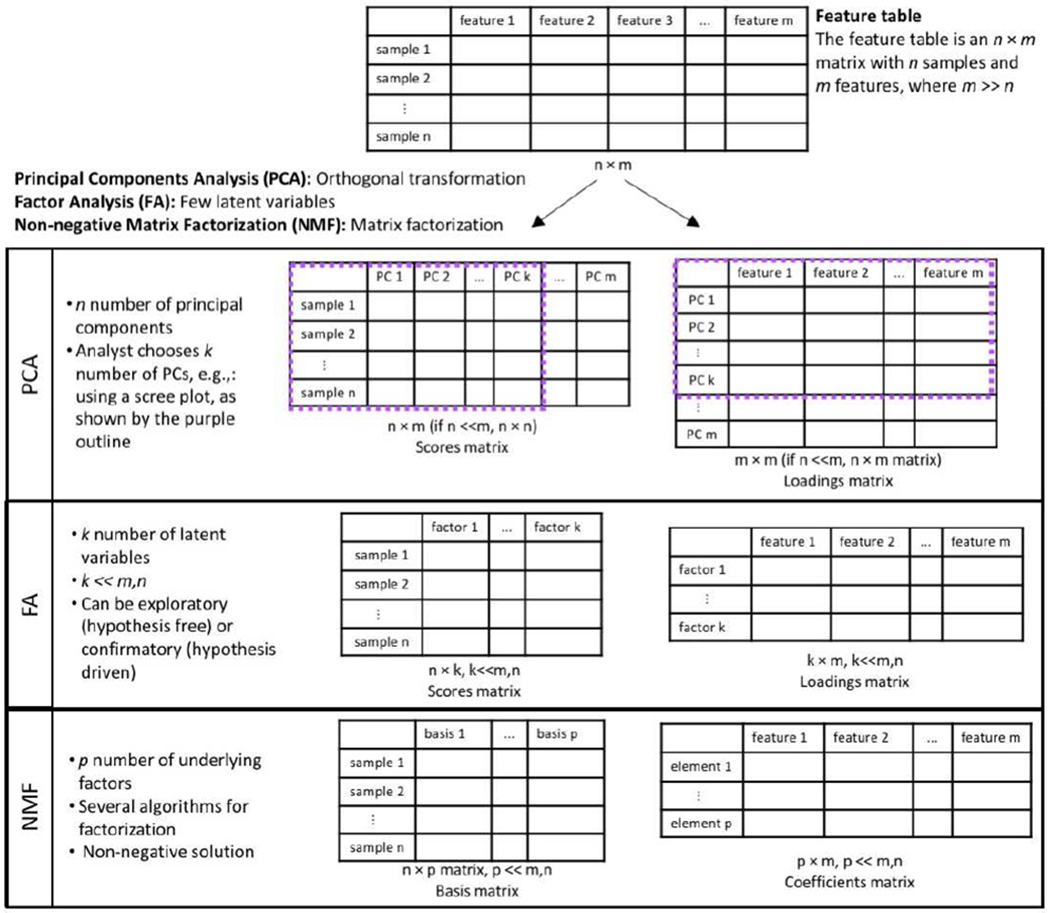
Visual representation of dimension reduction using PCA, FA, and NMF.

1. Principal components analysis (PCA)

Principal components analysis is one of the most commonly used approaches for dimensionality reduction. The method uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of linearly uncorrelated variables called principal components. The first component explains the most variance in the data and each succeeding component has the highest variance possible under the constraint that it is orthogonal, i.e., independent, to the preceding components [24]. The method does not reduce the number of variables, m variables produce m components. The analyst chooses the number of components to include in analyses based on some a priori defined criterion/a, e.g., looking at the scree plot, selecting components with eigenvalues above one, or selecting the number of components that explain a pre-specified proportion of the variance in the data, e.g., at least 75%. Since PCA forces orthogonality between components, it imposes a rigid structure [25]. The alternating least squares variant of PCA, independent component analysis, is more successful in dealing with this rigidity but has less compression in the first components [26].

In a study of 1301 European mother-child pairs, Tamayo-Uria et al. measured 87 environmental exposures during pregnancy and 122 exposures in early childhood. These included atmospheric, GIS, meteorological, built environment, SES, lifestyle, and biomarker data. The authors used PCA in two different ways. First, in the 19 pre-defined exposure groups, the first PC from each group was used as a composite index variable. Second, they used all exposure variables in the PCA and found that 65 and 90 PCs were needed to explain 95% of the variance in the pregnancy and early childhood exposome respectively [27]. In another study of 397 pregnant women in the Child Health and Development Studies in California, Li and colleagues investigated the relationship between 39 environmental chemicals and the serum metabolome. To reduce the dimensions and study the variance of the metabolome, they conducted a PCA on the high-resolution metabolomics data. The first PC explained 58.5% of the variance. They assessed the influence of the environmental chemicals by regressing the levels of contaminants measured on the first 10 PCs. They found the chlorinated pesticide metabolite DDE to be associated with the first four PCs and the parent pesticide DDT to be associated with PC 9 [28].

2. Factor analysis (FA)

Factor analysis aims to explain the covariance among variables and assumes that the underlying correlation patterns between variables arise from a few common latent variables called factors. The observed variables are defined as linear combinations of the factors, revealing the underlying constructs that give rise to the observed phenomenon. Then, factor loadings can be used to discern a pattern in the original variables, like exposomic features. Thus, FA finds a new set of variables, fewer in number than the original variables while expressing that which is common among the original variables. The analysis can be exploratory, where no assumptions are made about relationships among factors. It can also be confirmatory to test the hypothesis that the variables are associated with specific factors [29,30]. Most studies of the exposome take an exploratory approach, thus scientific concept or hypothesis underlying the factors is secondary to the analysis. Different models and methods of calculation can be used for the analyses, contributing to diversity in the methodology and results from factor analysis [31]. The analyst is required to choose the optimal number of factors that explain the data using model diagnostics, like the Bayesian information criterion (BIC). Confirmatory factor analysis relies on sophisticated math to confirm or test for generalizations [32]. Labelling interpretable factors identified as part of the underlying structure is a difficulty in factor analysis. It is a struggle to “see what there is and not what we want to see” [31].

Juarez and colleagues (2017) investigated the association between 2162 environmental exposures and lung cancer mortality rates in more than 2000 US counties using graph theoretical algorithms and factor analysis. They first computed correlation coefficients between each exposure-outcome pair, then used a clique doubling technique [33] to determine a threshold for significant correlation (r > |0.14|). They extracted paracliques [34,35] from graphs created using the significant threshold. To eliminate redundant information contained in the paracliques, the authors used factor analysis with varimax (orthogonal) rotation to obtain 172 factors that were subsequently used in stepwise regression on each of their outcomes of interest [36].

3. Non-negative matrix factorization (NMF)

In FA and PCA, latent variables and their errors are assumed normally distributed, and are thus not really suitable for non-negative data, such as exposome data. Non-negative matrix factorization was proposed by Lee and Seung as a solution [37,38]. This method works well with non-negative data that have excess zeros and measurement error, like measurement of chemicals and metabolites through HRMS [39]. NMF works to factorize a data matrix into two matrices, a basis matrix and a coefficient matrix—both are constrained to have non-negative values. The dimensions of the new matrices after factorization, i.e. number of underlying factors, has to be set by the analyst. No orthogonality constraints are placed on the basis components, allowing them to overlap. This overlap can be used to determine molecules that belong to multiple pathways or processes. The factorization produces sparse results with only a few non-zero entries [40]. The method has gained traction in systems biology and has been applied to transcriptomics data. According to Stein-O’Brien and colleagues, NMF learns two matrices—one that describes the structure between the molecules, genes or metabolites, and the other describes the structure between the different samples, i.e., each observation. They describe the first matrix as the amplitude matrix and the latter as the pattern matrix. The value in each column of the amplitude matrix can be thought to represent the relative contribution of a molecule in each inferred factor, which may be used to distinguish different complex biological processes or function pathways [41].

Béchaux and colleagues used NMF to extract patterns in the mixture of pesticides that derive from the major food consumption systems found in the French diet. They subsequently used the data to show clusters of individuals with similar consumption habits and exposure to pesticides. In order to determine the number of underlying latent structures (k), they ran NMF using different values of k and used residual sum of squares and the Bayesian information criterion (BIC) to choose the appropriate number, k=10 [39].

PCA, FA or NMF? The choice depends on the research question

When to use one of these methods depends mainly on the research question of interest. If the goal is to capture the total variance or a proportion of the variance in the data, PCA is the appropriate technique to employ. If the goal is to uncover a latent structure, an analyst can employ either NMF or factor analysis. NMF allows for better interpretation of the reduced dimensions because of the non-negative constraint; however, one can run into identifiability problems. To the best of our knowledge, NMF has not yet been applied in an exposomic context. In PCA, the analyst would have to decide on the appropriate number of components to extract from the solution based on a priori decided criteria. In factor analysis and NMF the number of factors is an analyst-defined input and different runs for different numbers of factors should be conducted before deciding on the optimal one, either in terms of data fit or/and interpretability of the solution. Nguyen and Holmes offer useful tips for dimensionality reduction [42]

A PCA Application: An HRMS Example

To illustrate an example of exposomic data dimensionality reduction, we analyzed respiratory exposures present in air using passive silicone badge samples and an untargeted GC-orbitrap assay developed for measuring the human exposome. Silicone badge samplers were placed in groups of four throughout different locations in two houses and a laboratory environment to evaluate the room and residence specific exposome near Atlanta, GA. The wristbands passively sampled chemicals present in the air of these locations for 7 days. These low-cost passive samplers allow access to micro- and personal-exposure from a large population and have potential as a key, exposome sampler for population research. Following deployment, samplers were weighed, placed in amber vials and extracted with 1mL ethyl acetate at room temperature with gentle shaking for 24 hours. The extracts were transferred to a GC autosampler vial, and analyzed in duplicate using full scan mode over m/z range 85-850 and a 15m Agilent DB-5MSUI capillary column with the following temperature gradient: 100°C for 1 min, increased to 180°C at 25°C/min; followed by a temperature ramp to 215°C at 5°C/min, and finally increased to 300°C at 25°C/min and held for 10 min, resulting in a total run time of 26.6 min. Detected ion signals were extracted using XCMS [43] at two different parameter settings and merged using xMSanalyzer [44].

A total of 49,585 features were detected in the 78 samplers from three different locations. In this example, we present results from one location, a house where samplers were placed in 6 different areas throughout the residence, a total of 23 samplers. Using a blank badge sampler as background, we retained a feature in the feature table if it was present at twice the blank intensity in at least 80% of the badge samplers. This reduced the number of detected features to 1347. The dimensions, thus, of the feature table for PCA was 23×1347. Missing data were imputed with half the lowest abundance of that feature. Data were log₁₀-transformed and used as input to the prcomp() function in R (version 3.6.0). The data were centered and scaled. The first five PCs explained 81.2% of the total variance. The biplot (Figure 2) shows grouping of exposomic features derived from wristbands placed in the same location.

Figure 2.

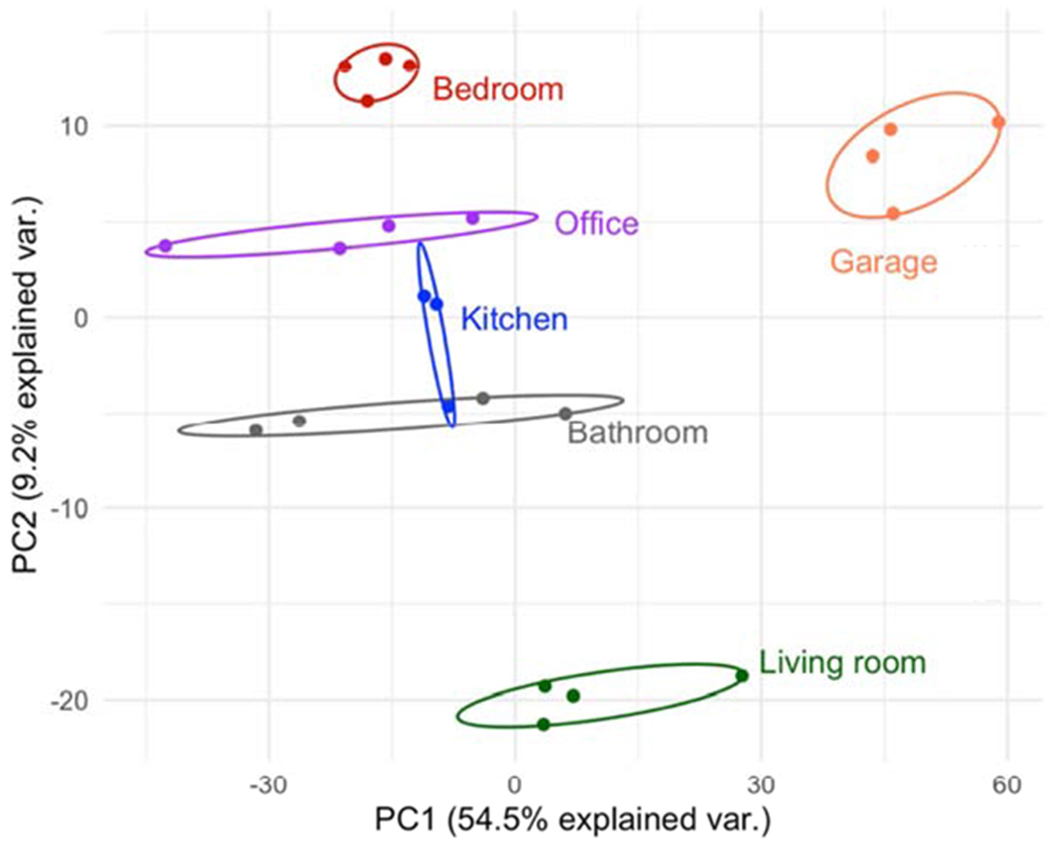
Biplot: Principal Component 1 (PC1; explained 54.5% of the total variance in the data) plotted against PC2 (explained 9.2% of the variance) showing clustering of samplers placed in the same location of house 2.

Discussion and conclusion

We discussed the application of three different unsupervised dimension reduction techniques that can be used in exposome research. While unsupervised, FA and NMF require analyst input to decide the optimal number of underlying factors that describe the observed phenomenon, but they reduce the number of independent variables. While PCA does not require analyst input during orthogonal transformation, input is required when selecting the number of PCs to extract and include in further analyses, since the total number of PCs equal the number of observations in original dataset. All three methods are sensitive to scale and data should be standardized before dimension reduction.

While dimensionality reduction removes redundant information, such as multiple ions present from one chemicals or highly correlated metabolites from the same biological pathway, these redundant signals are informative when evaluating chemical identifications and evaluating systemic biological response to exposure [45]. Further, simply creating new variables that are linear combinations of other variables can hinder interpretability of results. Chemical risk assessment is difficult to accomplish with linear combinations of multiple chemicals and researchers must attempt to report interpretable results from high-dimensional data. Lastly, generalizing latent structures from observed data should be performed cautiously. As noted by Alexandre Dumas (Junior), “all generalizations are dangerous, even this one” [32]. Here, we highlighted a few unsupervised methods for dimensionality reduction; however, to identify exposomic patterns specific to outcomes of interest, supervised extensions will likely need to be incorporated into the informatic workflow, e.g., the supervised PCA [46]. This paper illustrates that exposome research requires approaches to analyze the data that are as sophisticated as the approaches used to generate the data. In the future, a detailed simulation study would provide an opportunity to assess the performance of different supervised and unsupervised dimensionality reduction methods in exposomic research, given potential different research questions, to best inform the choice of method for data analysis.

Table 1.

Glossary of terms.

Term	Definition
Variance	$\frac{{\sum }_{i=1}^n{(x_i-\overline{x})}^2}{n-1}$; sample variance is usually interpreted as the average squared deviation from the mean
Covariance	$\mathit{cov}(x,y)={\sum }_{i=1}^N\frac{(x_i-\overline{x})(y_i-\overline{y})}{N}$; a measure used to quantify the relationship between two random variables
Correlation	$\mathit{cor}(x,y)=\frac{\mathit{cov}(x,y)}{{\sigma }_x{\sigma }_y}$; where σ denotes standard deviation; unlike covariance, correlation is a unitless measure of the relationship between two random variables
Orthogonal transformation	A linear transformation is called orthogonal if it preserves the length of the vectors; $\parallel T(\overrightarrow{x})\parallel =\parallel \overrightarrow{x}\parallel$. In PCA, the solution forces each component to be orthogonal to the previous, i.e., independent.
Matrix factorization	Decomposition of a matrix into the product of two or more lower-dimension rectangular matrices
Latent variable	An unobserved (“hidden”) variable that is inferred through observed variables
Bayesian Information Criterion (BIC)	Determines model fit by considering the likelihood function of a model, number of data points, and number of free parameters to be estimated. It is a criterion used for model selection; the model with lowest BIC is preferred.
Clique	In graph theory, a complete subgraph is called a clique. A graph is complete when every pair of distinct vertices—a corner or a point where lines meet—is connected by a unique edge, i.e., every vertex has an edge to every other vertex.
Paraclique	It consists of a clique and all vertices with at least some proportion of edges to the clique. It is considered a relaxation of clique.

Highlights.

• High-resolution mass spectrometry (HRMS) has enabled measurement of exposomic features in biomatrices

• HRMS poses data complexities that require dimensionality reduction

• Principal components analysis, factor analysis, and non-negative matrix factorization have been successfully applied in exposomic data analysis

• Interpretability of results after dimensionality reduction is essential for environmental policy and risk assessment