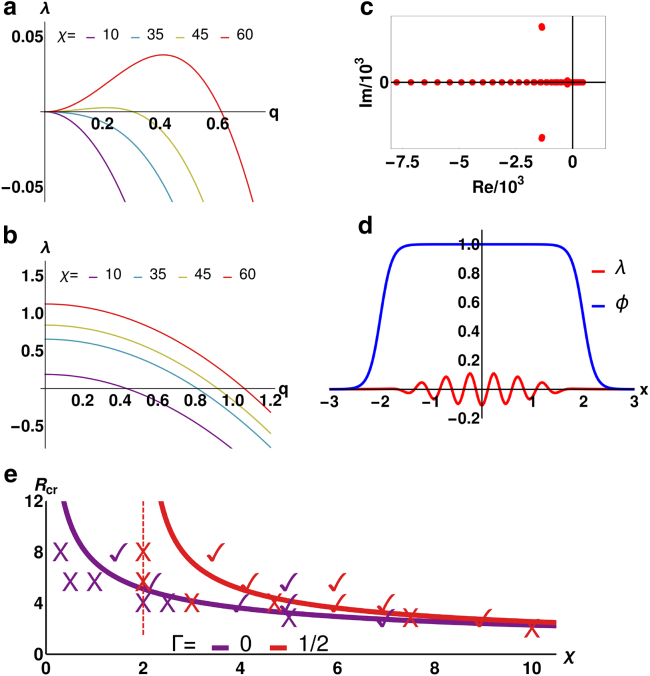
Figure 2.

Linear stability analysis: (a and b) ϕ = 1 (no droplet confinement); growth rate λ(q) of small fluctuations around the uniform phase with friction (Γ = 1, a) and without (Γ = 0, b). (c and d) ϕ$\ne$ 1: red dots show eigenvalues λ₁ … λ_N, whose real parts determine the growth rate of actomyosin-fluctuations within a droplet. Dots right of the Re = 0-line represent unstable modes; the fastest growing one shown in (d) represents instability within the droplet and its suppression at the droplet boundaries, meaning contractility-induced cell motility can only occur in large enough cells (see Supporting Materials and Methods). Parameters: χ = 4.5; R = $\sqrt{V/\pi }$ = 2 and L = 3; dx = 0.01; N = 601 (for discretization); others as in simulations. (e) shows χ-dependent critical cell radii for different Γ. Symbols ✓ (cell motion) and X (no motion) correspond to parameters of simulation runs and are in agreement with our linear stability analysis. Dashed lines show critical χ-values, below which contractility-induced motility is impossible, even for very large cells. To see this figure in color, go online.