Yeast ATM and ATR kinases use different mechanisms to spread histone H2A phosphorylation around a DNA double-strand break

Significance

Creation of a chromosomal double-strand break (DSB) is rapidly accompanied by extensive phosphorylation of yeast histone H2A isoform (H2AX in mammals) by Mec1 (ATR) and Tel1 (ATM) protein kinases. This phosphorylation, termed γ-H2AX, spreads 50 kb on either of the DSB, but how this phosphorylation is propagated is poorly understood. We have monitored the kinetics and extent of spreading individually for Mec1 and Tel1 and find that the patterns of spreading are significantly different for the two kinases. By comparing these experimental data to mathematical models of spreading, either by one-dimensional (1D) or 3D diffusion, we report that Bayesian model selections suggest Tel1 acts by directed motion along a chromatin fiber, whereas Mec1 primarily uses a 3D mode of propagation.

Abstract

One of the hallmarks of DNA damage is the rapid spreading of phosphorylated histone H2A (γ-H2AX) around a DNA double-strand break (DSB). In the budding yeast Saccharomyces cerevisiae, nearly all H2A isoforms can be phosphorylated, either by Mec1^ATR or Tel1^ATM checkpoint kinases. We induced a site-specific DSB with HO endonuclease at the MAT locus on chromosome III and monitored the formation of γ-H2AX by chromatin immunoprecipitation (ChIP)-qPCR in order to uncover the mechanisms by which Mec1^ATR and Tel1^ATM propagate histone modifications across chromatin. With either kinase, γ-H2AX spreads as far as ∼50 kb on both sides of the lesion within 1 h; but the kinetics and distribution of modification around the DSB are significantly different. The total accumulation of phosphorylation is reduced by about half when either of the two H2A genes is mutated to the nonphosphorylatable S129A allele. Mec1 activity is limited by the abundance of its ATRIP partner, Ddc2. Moreover, Mec1 is more efficient than Tel1 at phosphorylating chromatin in trans—at distant undamaged sites that are brought into physical proximity to the DSB. We compared experimental data to mathematical models of spreading mechanisms to determine whether the kinases search for target nucleosomes by primarily moving in three dimensions through the nucleoplasm or in one dimension along the chromatin. Bayesian model selection indicates that Mec1 primarily uses a three-dimensional diffusive mechanism, whereas Tel1 undergoes directed motion along the chromatin.

Genetic loci can be separated by thousands to millions of base pairs in the nucleus, limiting contacts between distant regions of the genome. Yet many biological processes rely on the effective communication between distant parts of the genome to facilitate a diverse range of phenomena such as the regulation of gene expression through promoter−enhancer interactions, the formation of chromatin loops during chromosome condensation, or the initiation of homologous recombination in the presence of DNA breaks (1–3). Therefore, an understanding of many nuclear processes can be uncovered by investigating how distant chromosomal regions can establish genomic interactions in a timely fashion (4).

Communication between remote parts of the genome is often facilitated by the presence of intermediary proteins that shuttle information in a three-dimensional (3D) manner through the nucleoplasm or in a 1D manner along the chromatin. The 3D modes of communication lead to both intrachromosomal and interchromosomal interactions either by the physical folding of chromatin to bring two regions of the genome within close proximity (looping) or by 3D diffusion of a protein from one genetic loci to another through the surrounding nucleoplasm (5). In both looping and 3D diffusion, information can be transferred over many kilobases without having to interact with the intervening chromatin. In contrast, 1D mechanisms are intrinsically intrachromosomal, and communication is predicated on the movement of DNA-bound proteins along the contours of the chromatin fiber. The 1D mechanisms include either diffusive or unidirectional motion of proteins along the chromatin (5). Comparisons of experimental data with biophysical models of chromatin looping, 3D diffusion, 1D diffusion, and directed sliding provide insight into how communication of genomic elements occurs in the nucleus.

In particular, we are interested in studying how genomic interactions are achieved over a distance of many kilobase pairs after DNA damage. The rapid formation of γ-H2AX, the phosphorylated form of histone H2A (H2AX in mammals), over an extensive region of the chromatin is an indicator of DNA double-strand breaks (DSBs) (6–9). In budding yeast, γ-H2AX is formed by the phosphorylation at H2A-S129 by the checkpoint kinases Mec1 and Tel1, homologs of mammalian ATR and ATM, respectively. Previous studies have shown that Mec1 and Tel1 are both capable of forming γ-H2AX regions up to 50 kb on either side of a DSB (9), while their mammalian homologs, especially ATM, are able to phosphorylate histones in chromatin regions in excess of 1 Mb in mammalian cells (6, 7). γ-H2AX has been shown to play a role in the recruitment and retention of factors responsible for efficient DNA repair, DNA damage signaling, and chromatin remodeling, although it is not essential for these processes (10).

Mec1 and Tel1 are activated in the presence of a DSB by different mechanisms. In budding yeast, as in mammals, Tel1^ATM is attracted to a broken chromosome end by its association with Mre11–Rad50–Xrs2^Nbs1 (11). In contrast, the recruitment of Mec1^ATR requires that the broken end undergoes some 5′ to 3′ resection, promoting the binding of the single-strand DNA-binding protein complex, RPA. RPA is then bound by Ddc2^ATRIP, which is the obligate partner of Mec1^ATR (12, 13). While we know that both Mec1 and Tel1 are actively recruited to DSBs and are involved in γ-H2AX formation, the means by which Mec1 and Tel1 kinases reach histones tens of kilobases from the DSB is still unknown. To address this problem, we monitored the kinetics and extent of γ-H2AX formation in budding yeast, by chromatin immunoprecipitation (ChIP)-qPCR, after creating a synchronously induced DSB at a specific location on chromosome III. We compared experimentally measured γ-H2AX distributions to mathematical formulations of different phosphorylation spreading mechanisms to determine whether the kinases can reach histones far from the DSB using chromatin looping, 3D diffusive, 1D diffusive, or directed sliding mechanisms. Using Bayesian model selection, we propose that Mec1 reaches target histones by a 3D diffusive mechanism, while Tel1 dynamics are best described by directed 1D sliding along the chromatin.

Results

Mec1 and Tel1 Kinases Use Different Mechanisms for γ-H2AX Spreading.

We studied phosphorylation spreading in Saccharomyces cerevisiae after inducing a site-specific DSB using a galactose-inducible HO endonuclease, resulting in robust cleavage at the MAT locus on chromosome III within 30 min (SI Appendix, Fig. S1). DSBs were rendered irreparable by homologous recombination through the deletion of both HML and HMR donor loci (14, 15). γ-H2AX spreading was studied in G1-arrested haploid MATa cells where the relegation of cleaved ends by nonhomologous end-joining was prevented by deleting NEJ1 or YKU80 (14, 16–18). The formation of γ-H2AX over a region of roughly 50 kb on both sides of the DSB was quantified by ChIP-qPCR with an antibody specific to phosphorylated H2A-S129. In order to differentiate the mechanisms used by Mec1 and Tel1 to phosphorylate large regions of chromatin adjacent to the break, we measured γ-H2AX levels in strains where both Mec1 and Tel1 were active or when only Mec1 or Tel1 kinase was active.

In G1-arrested cells, 5′ to 3′ resection of DSB ends is blocked (19). Under these conditions, the absence of RPA binding leads to lack of Mec1 recruitment, so only Tel1 is active (9). We confirmed that, in nej1∆ G1-arrested cells, Tel1 robustly modifies the chromatin adjacent to MAT, but there is only a very small signal in strains where only Mec1 is present; the observed signal likely reflects the small fraction of cells that have escaped α-factor arrest (Fig. 1 A and B).

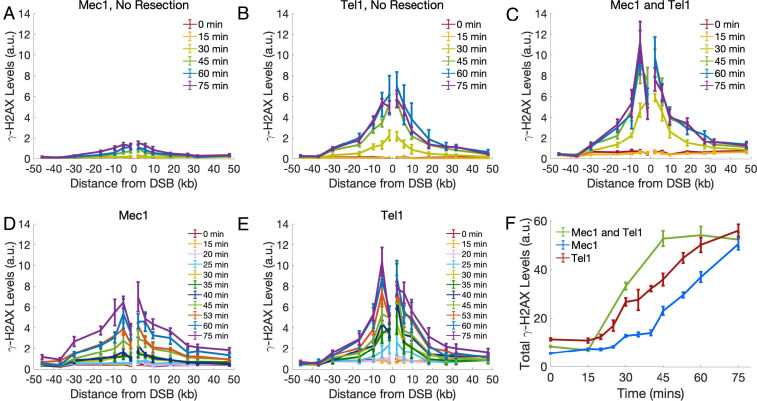
Fig. 1.

Experimental γ-H2AX profiles by Mec1 and Tel1. γ-H2AX spreading as measured by ChIP-qPCR after generating a break at the MAT locus. All cells were arrested in G1 with end-joining prevented by nej1∆ or yku80∆. In all plots, error bars represent SEM from n ≥ 3 measurements. (A) γ-H2AX spreading by Mec1 in nej1∆ cells. (B) γ-H2AX spreading by Tel1 in nej1∆ cells. (C) γ-H2AX spreading by both Mec1 and Tel1 in ku80∆ cells. (D) γ-H2AX spreading by Mec1 in ku80∆ cells. (E) γ-H2AX spreading by Tel1 in ku80∆ cells. (F) Total γ-H2AX levels by both Mec1 and Tel1 (green), only Mec1 (blue), and only Tel1 (red) in ku80∆ cells.

To compare Mec1 and Tel1 activity in G1 cells, we deleted YKU80, which normally blocks access of the exonuclease Exo1 to the DSB (20). The yku80∆ cells generate sufficient single-stranded DNA (ssDNA) to recruit the single-strand binding protein complex RPA and activate Mec1-Ddc2 (20, 21). Under these conditions, both Mec1 alone or Tel1 alone were efficient at phosphorylating histone H2A (Fig. 1 D and E). In the absence of YKU80, the Tel1-only derivative exhibited a significant increase in γ-H2AX levels over background by 25 min (Fig. 1E), when about 60% of the MAT locus had been cleaved (SI Appendix, Fig. S1). The appearance of γ-H2AX in the Mec1-only strain was delayed by about 5 min (Fig. 1D). In both cases, the extent of phosphorylation was largely complete by 75 min, but with noticeable differences between the phosphorylation profiles of Mec1 and Tel1. Although Tel1 appears to be more rapidly activated, the extent of γ-H2AX spreading is more confined to the region adjacent to the break than Mec1. The difference in the profiles of modification can be shown by calculating the mean modification distance (MMD), the distance from the break that encompasses half of the γ-H2AX profile. At 75 min, the 95% CI for the MMD of Mec1 is MMD_Mec1 = [12.9, 14.5] kb, while the 95% CI for the MMD of Tel1 is MMD_Tel1 = [10.8, 11.6] kb, indicating that the activities of Mec1 and Tel1 lead to significantly different profiles of spreading (SI Appendix, Fig. S2A).

When both kinases are active, the kinetics of phosphorylation were more rapid and reached an apparent steady state around 45 min, suggesting that both Mec1 and Tel1 participate in phosphorylating H2A (Fig. 1 C and F). We also note that, at later time points, the level of modification close to the DSB does not increase as the loss of nucleosomes during 5′ to 3′ resection displaces histones at a rate of 4 kb/h (22). Although the γ-H2AX profiles for each kinase alone or when both are active differ in their kinetics and extent of spreading, the total amount of γ-H2AX formation is the same by 75 min, suggesting that Mec1 and Tel1 have similar levels of phosphorylation activity, but distribute the γ-H2AX sites differently (Fig. 1F and SI Appendix, Fig. S2B).

The Amount, but Not the Profile, of γ-H2AX Is Affected by Reducing the Density of Phosphorylation Sites.

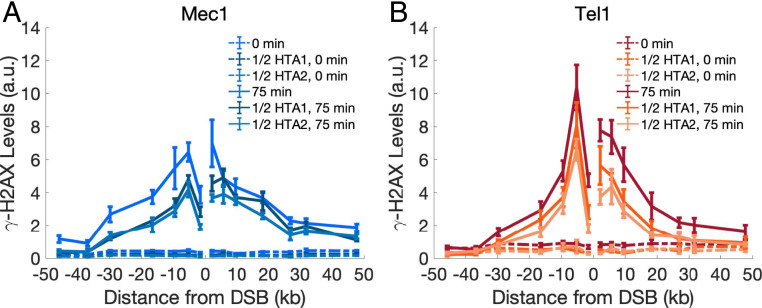
To further investigate the differences between the Mec1 and Tel1 modes of spreading, we mutated the phosphorylation site of one or the other H2A gene. Using CRISPR-Cas9, we mutated either HTA1-S129 or HTA2-S129 to alanine (SI Appendix, Experimental Methods), so that the density of phosphorylatable H2A-S129 sites should be reduced by half. As expected, each of these mutations reduced the level of γ-H2AX (Fig. 2 and SI Appendix, Fig. S2B), suggesting that the availability of H2A phosphorylation sites is limiting; that is, the amount of γ-H2AX formed depends on the density of phosphorylatable sites. Despite the reduction in γ-H2AX levels, the profile of phosphorylation spreading for Mec1 and Tel1 remains unchanged when only 50% of the sites can be phosphorylated; moreover, the two mutant profiles were not significantly different from each other. The 95% CI of the MMDs at 75 min for Mec1 are $\mathrm{MM}{\mathrm{D}}_{\mathrm{Mec}1,\mathrm{HTA}1}=\left[13.2,\hspace{0.17em}14.4\right]\mathrm{kb}$ and $\mathrm{MM}{\mathrm{D}}_{\mathrm{Mec}1,\mathrm{HTA}2}=\left[13.0,\hspace{0.17em}14.2\right]\mathrm{kb}$, while the 95% CI of the MMDs for Tel1 are MMD_Tel1,HTA1 = [10.0, 10.8] kb and MMD_Tel1,HTA2 = [10.7, 11.9] kb (Fig. 2 and SI Appendix, Fig. S2A).

Fig. 2.

Experimental γ-H2AX profiles by Mec1 and Tel1 when 50% of H2A sites cannot be phosphorylated. Phosphorylation spreading in strains where one of the two HTA genes is mutated to HTA-S129A, rendering half the H2A sites nonphosphorylatable. Experimentally measured γ-H2AX profiles by (A) Mec1 or (B) Tel1 are shown for 0 min (dashed lines) and 75 min (solid lines); “1/2 HTA1” refers to the presence of an hta2-S129A mutation, while “1/2 HTA2” carries the hta1-S129A mutation. Error bars represent SEM from n ≥ 3 measurements.

Mec1 Modifies Histones at Distant Chromosome Sites That Are Recruited to the DSB.

A DSB near one centromere will lead to the modification of all of the other 15 pericentromeric regions clustered at the spindle pole body (23). This modification is predominantly carried out by Mec1 and occurs at about 1/10 the magnitude as modifications on the broken chromosome (23). γ-H2AX is also weakly spread around the recombination enhancer, RE, a sequence roughly 170 kb from MAT, that facilitates pairing between MATa and the HML donor (24). RE binds multiple copies of the Fkh1 protein whose FHA domain can presumably also bind to phosphothreonines that are generated near the DSB; however, the specific phosphorylated target remains unknown. ChIP using an anti−γ-H2AX antibody pulls down the RE region in MATa cells, when Fkh1 binds to RE, but not in MATα cells, when Fkh1 binding is repressed (25). Thus, a kinase originating at the MAT locus can only phosphorylate the region around RE by 3D diffusive or looping mechanisms, and only when it has been brought into proximity with the DSB. In our strains, HML is deleted, but the Fkh1 proteins bound to RE are still able to interact with phosphorylated targets near MAT. At 75 min, the level of ChIP-qPCR 10 kb away from RE was significantly increased above background for Mec1 (SI Appendix, Fig. S3A), while Tel1 did not show a significant increase at these distances, except possibly at the −5-kb location (SI Appendix, Fig. S3B). Taken together, the experimental evidence suggests that Mec1 is the kinase that is primarily responsible for phosphorylation spreading in trans.

Biophysical Models of Chromatin Modification Spreading Can Be Used to Determine the Mechanism by which Mec1 and Tel1 Phosphorylate Distant H2As.

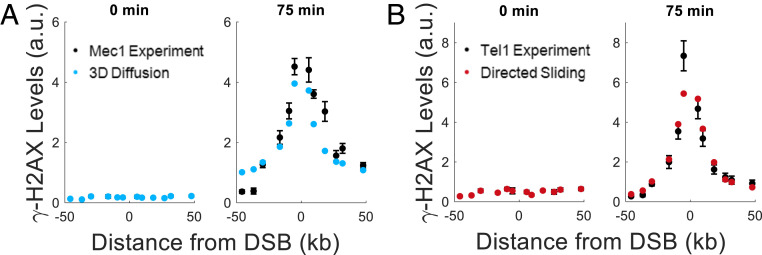
By comparing the phosphorylation data to mathematical models of phosphorylation spreading, we can infer the mechanisms by which the kinases spread γ-H2AX. We focused on two classes of models, one of which assumes that spreading occurs by the kinase moving three-dimensionally through the nucleoplasm, while the other assumes that kinases move one-dimensionally along the chromatin. For each class, we chose two minimal models commonly found in the literature (5): The 3D models are represented by chromatin looping and 3D diffusion, while the 1D models are represented by 1D diffusion and directed sliding (Fig. 3) (SI Appendix, Model Derivations). All four models assume an initial recruitment of the kinases to the break site with a rate k_init, but differ thereafter. For the 1D models, the parameter k_init comprises both the recruitment and detachment from the DSB to begin traversing the chromosome. Although each nucleosome contains two monomers of H2A, in these models, we treat each phosphorylation site as a separate entity.

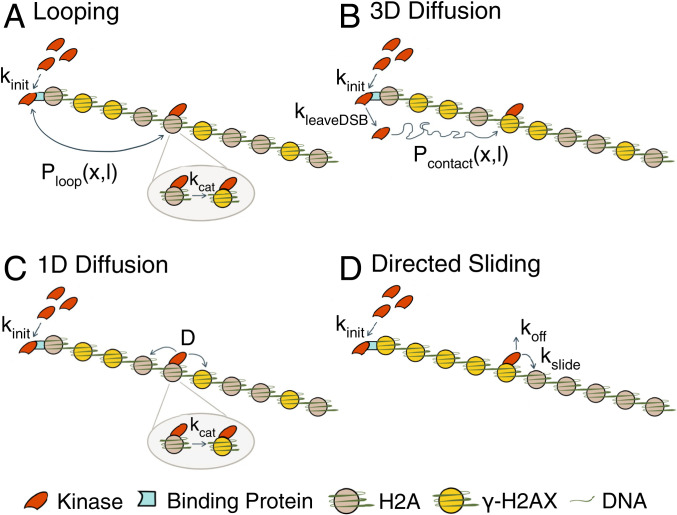
Fig. 3.

Schematic of phosphorylation spreading mechanisms. Schematics of (A) looping, (B) 3D diffusion, (C) 1D diffusion, and (D) directed sliding mechanisms. The kinases Mec1 and Tel1 (red) are recruited to the DSB at a rate k_init to RPA and MRX respectively (teal). For 1D diffusion and directed sliding, k_init comprises both the recruitment to and detachment from the DSB of the kinase to begin translocating along the chromatin. The kinase proceeds to phosphorylate H2A (gray) to form γ-H2AX (yellow) using one of the four mechanisms. (A) In looping, the kinase remains tethered at the DSB and forms a looped conformation with probability P_loop(x,l), where x = distance in kilobases of the target H2A from the break and l is the chromatin Kuhn length. P_loop(x,l) is formulated using a worm-like chain polymer model. The kinase phosphorylates H2A at a rate k_cat after contact. (B) In 3D diffusion, the kinase transiently binds to the DSB where it is activated and released at a rate k_leaveDSB. The activated kinase diffuses away from the DSB until it encounters and phosphorylates H2A. P_contact(x,l) is the probability that the kinase comes into contact with an H2A located a distance x away from the break. (C) In 1D diffusion, the kinase is recruited to the DSB and proceeds to move along the chromatin with a 1D diffusion coefficient D. The kinase phosphorylates H2A that it comes into contact with at a rate k_cat. (D) In directed sliding, the kinase moves unidirectionally away from the DSB along the chromatin. The kinase slides onto adjacent histones at a rate k_slide and phosphorylates all H2As encountered until the kinase detaches from the chromatin at a rate k_off.

Thermal fluctuations can lead to the formation of transient chromosomal loops. In the looping model (Fig. 3A), the kinase is tethered at the break end, and folding of the chromatin brings distant H2As into physical contact with the DSB-bound kinase. Using a worm-like chain model of the chromosome, we compute P_loop(x, l), the probability of a looped conformation in which the DSB-bound kinase is in contact with an H2A located x kilobases away, where l is the Kuhn length of the chromatin. When the kinase is in contact with an H2A, phosphorylation occurs at a rate k_cat.

The 3D diffusion model (Fig. 3B) assumes that the kinase briefly binds to the DSB, where it is activated, and then released at a rate k_leaveDSB. The activated kinase diffuses through the nucleoplasm until it encounters and phosphorylates an H2A site. For an H2A located x kilobases from the DSB, we use the worm-like chain polymer model to calculate the mean 3D distance between this H2A and the DSB. This distance is used to compute the probability P_contact(x, l) that the kinase will come into contact with the H2A.

The 1D diffusion model (Fig. 3C) assumes that the kinase lands at the DSB and moves along the chromatin with the one-dimensional diffusion coefficient D, phosphorylating histone H2A at a rate k_cat. The directed sliding model (Fig. 3D) is similar to 1D diffusion except that the kinase moves unidirectionally away from the DSB along the chromatin. The kinase slides onto adjacent histones at a rate k_slide and phosphorylates all H2As that it comes across until the kinase detaches from the chromatin at a rate k_off.

For an H2A located x kilobases from the break site, each of our models predicts the probability P(x,t) that the histone has been phosphorylated at time t after the DSB induction. Each model predicts a distinct P(x,t), allowing us to use the experimentally measured γ-H2AX profiles to determine the best spreading models for Mec1 and Tel1. However, before we can directly compare the theoretical predictions to experimental measurements, it is necessary to convert the predicted probabilities P(x,t) to the expected ChIP signals. We formulate a simple thermodynamic model for the ChIP pulldown to account for the binding of antibodies to a chromatin fragment containing multiple phosphorylated H2As (SI Appendix, Fig. S4). Sonication during ChIP results in chromatin fragments of roughly 500 bp. We introduce the following model parameters: N_H2A, f, and C. The parameter N_H2A represents the average number of H2As on the chromatin fragment, and f is the probability that each γ-H2AX is bound by an antibody; we assume that the γ-H2AX−antibody interaction is independent of the other γ-H2AXs on the same chromatin fragment. We also make the assumption that the presence of one γ-H2AX−antibody interaction is sufficient for pulling down the entire chromatin fragment during ChIP. Finally, C accounts for the loss in DNA recovery during the wash steps of ChIP. We derive the ChIP model in detail in SI Appendix, Model Derivations.

Bayes Factors Reveal the Most Likely Phosphorylation Spreading Mechanisms for Each Kinase.

The best model for each kinase was determined by calculating the Bayes factor which expresses how much less probable one model is compared to another model, given all of the data collected in our experiments. We take into account the γ-H2AX profiles around the DSB (Fig. 1 D and E) as well as the phosphorylation in trans near the RE locus (SI Appendix, Fig. S3). We first computed the Bayes factors for Tel1 alone (Table 1). The 1D models are vastly more likely than the 3D models. Next, we simultaneously computed the Bayes factors for both 1D models of Tel1 and either 1D or 3D models for Mec1, by imposing the constraint that the ChIP model parameters (C, f, and N_H2A) must be the same. Simultaneous pairwise calculations of the Bayes factor for both Mec1 and Tel1 models (excluding the 3D models for Tel1) are shown in Table 2; further details can be found in SI Appendix, Bayes Factor Calculation.

Table 1.

The log₁₀(Bayes factor) for Tel1

Model for Tel1	log10(Bayes factor)
Directed sliding	Best model
1D diffusion	−5
3D diffusion	−61
Looping	−251

Bayes factors were calculated by dividing the probability of the indicated model by the probability of the best model. The log₁₀(Bayes factor) is shown for Tel1 models.

Table 2.

log₁₀(Bayes factor) for various model combinations

Model combination	log10(Bayes factor)
Mec1 - 3D diffusion & Tel1 - directed sliding	Best model
Mec1 - 3D diffusion & Tel1 - 1D diffusion	−6
Mec1 - 1D diffusion & Tel1 - directed sliding	−12
Mec1 - 1D diffusion & Tel1 - 1D diffusion	−18
Mec1 - directed sliding & Tel1 - directed sliding	−35
Mec1 - directed sliding & Tel1 - 1D diffusion	−20
Mec1 - looping & Tel1 - directed sliding	−259
Mec1 - looping & Tel1 - 1D diffusion	−258

Bayes factors were calculated by dividing the probability of the indicated model by the probability of the best model. The log₁₀(Bayes factor) is shown for Mec1 and Tel1 simultaneously, based on 1D Tel models.

After determining the best models for Tel1 and Mec1, we implemented Bayesian parameter estimation to find the optimal values for the model parameters (Table 3) by fitting the data simultaneously in Figs. 1 D and E and 2 and SI Appendix, Fig. S3 A and B to the best models. The best models, plotted using the optimal parameter values, are in quantitative agreement with experimental data (Fig. 4). The less likely models are plotted against data in SI Appendix, Figs. S5–S16.

Table 3.

Parameter values for the best models

Te1, directed sliding	Mec1, 3D diffusion	Parameters shared by Mec1 and Tel1
kinit: 0.033/min (0.0060 to 0.077)	kinit: 0.089/min (0.068 to 0.15)	C: 26 (13 to 280)
kslide: 3.2 kb/min (2.0 to 17)	l: 14 kb (9.9 to 15)	f: 0.16 (0.020 to 0.72)
koff: 0.30/min (0.17 to 1.8)	ω: 4.2 × 10−3/min (1.1 × 10−3 to 5.0 × 10−3)	NH2A: 6 (2 to 6)

Optimal parameter values were obtained by simultaneously performing Bayesian parameter estimation for Mec1 and Tel1. The 95% CI for the parameter values are shown in parentheses. A description of the parameters can be found in SI Appendix, Model Derivations.

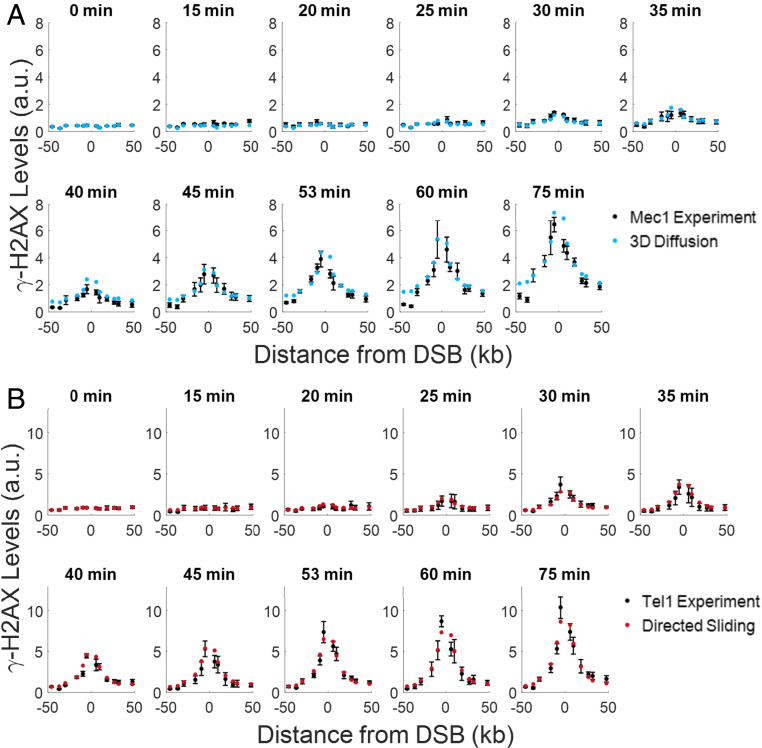
Fig. 4.

Comparison of experimental γ-H2AX profiles to the most likely theoretical spreading distributions. Comparison of experimental γ-H2AX profiles (black) to theoretical γ-H2AX distributions for the best model. (A) Experimental and theoretical curves for 3D diffusion (blue) by Mec1 phosphorylation. (B) Experimental and theoretical curves for directed sliding (red) by Tel1. The experimental error bars represent the SEM from n ≥ 3 measurements. The theory curves are plotted using parameters values shown in Table 3. Due to concerns about the reduction in γ-H2AX signal from resection close to the DSB, the −1.6-kb and 2.1-kb data points were excluded when performing fits to the experimental data. For the plots in A and B, our theoretical predictions start from the same background levels as in the experimental data.

In SI Appendix, Fig. S3C, we plot the predicted phosphorylation levels by Mec1 around RE. When modeling γ-H2AX spreading around RE, we include two additional parameters, which take into account the binding of RE to MAT (SI Appendix, Model Derivations). We did not plot the predicted phosphorylation by Tel1 near RE, because the directed sliding model predicts that RE is too far away from the DSB for Tel1 to act.

Theoretical Predictions of Phosphorylation Spreading Are in Agreement with Data from Mutant Strains in which 50% of the H2As Are Phosphorylatable.

Next, we compared the measured γ-H2AX levels from the 50% phosphorylatable strains to the theoretical predictions of the 3D diffusion model for Mec1 and the directed sliding model for Tel1 (Figs. 2 and 5), when only one out of every two H2As can be phosphorylated. We used the same parameter values for the 50% phosphorylatable strains as those used to fit the wild-type H2A strains (Fig. 4 and Table 3). The theoretical predictions for the 50% phosphorylatable strains are largely in agreement with the experimental data (Fig. 5).

Fig. 5.

Comparison of experimental and theoretical γ-H2AX profiles in strains where 50% of H2A sites cannot be phosphorylated. Experimentally measured γ-H2AX distributions for the HTA-S129A mutants were averaged together for each kinase. In A and B, theoretical curves were generated using the parameters listed in Table 3 for both (A) 3D diffusion by Mec1 (blue) and (B) directed sliding by Tel1 (red), respectively, and overlaid onto the experimentally measured 50% γ-H2AX profile (black).

The introduction of the S129A mutant allele did not affect the sliding rate of Tel1. We performed fits in which the HTA-S129A strains were allowed to have both k_slide and k_off differ from the parameter values established for the wild-type H2A strains. The sliding parameters remain unchanged in the HTA-S129A mutants, with the optimal k_slide and k_off values being within 10% of the established rates for wild-type H2A strains. Moreover, the Bayes factor calculation showed that the most likely directed sliding model for Tel1 is one in which k_slide and k_off are unaltered in the 50% phosphorylatable strains. From our Bayesian parameter estimation, the average distance over which Tel1 slides is 11 kb (95% CI of 9.7 kb to 12 kb) before falling off the chromosome.

The agreement between theory and experiments on HTA-S129A mutants also validates our model of the ChIP process, which provides us with a quantitative understanding of the relationship between the amount of γ-H2AX on the chromatin and the DNA recovery from ChIP (SI Appendix, Fig. S4). The recovery of >50% of the ChIP signal when one H2A gene is rendered nonphosphorylatable (SI Appendix, Fig. S2B) is explained by the assumption that there is a substantial chance that a DNA fragment will be pulled down even if there is only one γ-H2AX on the ∼500-bp DNA fragment (SI Appendix, Fig. S4). Even though the H2A-S129A strains have half as many γ-H2AX per fragment, there are still enough γ-H2AXs per fragment to be recovered with ChIP (SI Appendix, Model Derivations).

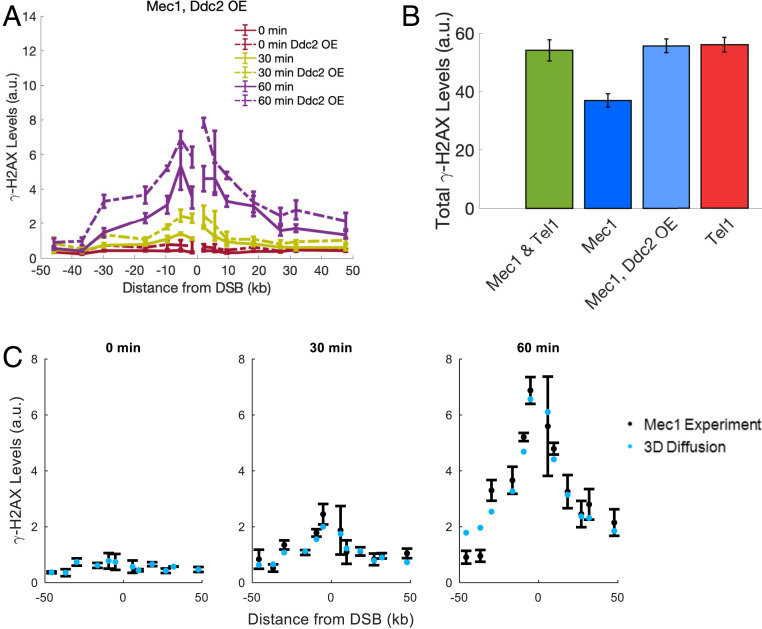
Phosphorylation Levels by Mec1 Are Improved by Overexpressing Its Binding Partner Ddc2.

Ddc2 overexpression was previously shown to increase Mec1’s checkpoint activity, whereas increasing Mec1 expression had no consequence (26). We therefore asked whether the efficiency of H2A modification by Mec1 could be improved by increasing the abundance of Ddc2. We integrated plasmid PML105.45, which contains an extra copy of Ddc2 under a GAL1 promoter, at leu2-3,112 in the tel1Δ yku80∆ strain (26, 27). Indeed, increased expression of Ddc2 in this Mec1-only strain increased the amount of γ-H2AX (Fig. 6A). In this instance, the total amount of γ-H2AX by Mec1 at 60 min in the Ddc2 overexpressed strains is nearly the same as that measured for the Tel1-only strain (Fig. 6B). However, the distribution of γ-H2AX sites is unaltered by the overexpression of Ddc2, since the MMD was unchanged from that seen in the absence of Ddc2 overexpression (SI Appendix, Fig. S2A). The 95% CI for the MMD for the Ddc2 overexpression case is given by MMD_{Mec1,Ddc2 O/E} = [12.5, 14.1] kb, while the MMD for Mec1 is MMD_Mec1 = [12.9, 14.5] kb, revealing that the mechanism by which Mec1 acts, whether it binds, activates, and diffuses or binds, activates, and remains bound, is not intrinsically dependent on its abundance.

Fig. 6.

γ-H2AX profiles by Mec1 with Ddc2 overexpression. (A) Overexpression of Ddc2 leads to increased γ-H2AX levels by Mec1. Experimental error bars represent the SEM from n = 2 measurements. (B) Overexpression of Ddc2 increases the total amount of phosphorylation by Mec1 (blue compared to light blue). By 60 min, Ddc2 overexpression raises the amount of γ-H2AX formed to those of Tel1-mediated phosphorylation levels (light blue compared to red). Error bars were calculated by error propagating over the error of the γ-H2AX profiles at 60 min for the associated strain. (C) Comparison of the 3D diffusion model (blue) with the experimental γ-H2AX levels (black). Experimental error bars represent the SEM from n = 2 measurements. Predicted levels of γ-H2AX were calculated by treating the initial recruitment rate k_init as a free parameter and by using the optimal parameters found for Mec1 mediated phosphorylation under wild-type levels of Ddc2 expression (Table 3).

To determine the effects of Ddc2 overexpression and further test the 3D diffusion model of phosphorylation spreading by Mec1, we compared the theoretical model to the Ddc2-overexpressed strain. Since Ddc2 forms an obligate heterodimer with Mec1 prior to its loading onto RPA-coated ssDNA (28), the overexpression of Ddc2 should lead to an increased rate of Mec1 recruitment, k_init. Treating k_init as a free parameter, while constraining all other model parameters to their previous values, we find that the 3D diffusion model agrees with the experimental data from the Mec1 strains in which Ddc2 is overexpressed (Fig. 6C). The optimal k_init is 0.25/min, 2.8 times the optimal k_init for the Mec1-only strains where Ddc2 is expressed at wild-type levels.

rad9∆ Does Not Alter the Extent of Phosphorylation Spreading.

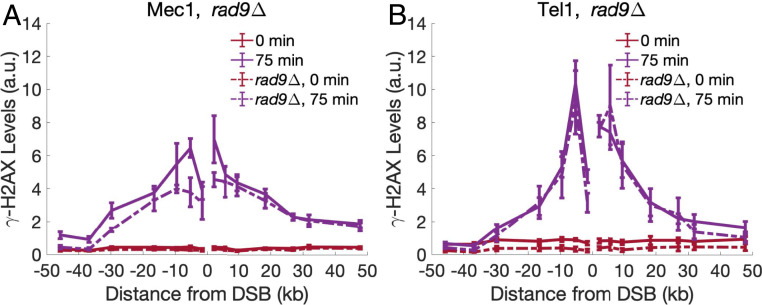
The same mathematical formulation used to encode the directed sliding model can also be used to describe a recruitment/assembly mechanism, where the arrival of a protein to the break facilitates recruitment of subsequent proteins until a string of proteins is formed spanning many nucleosomes. In this scenario, the rate of recruitment of the next protein copy is analogous to k_slide. This recruitment/assembly process has been suggested to occur in mammalian cells where the propagation of ATM down the chromosome is, in part, facilitated by the γ-H2AX binding proteins MDC1 and possibly 53BP1 (29, 30). MDC1 is capable of recruiting the MRN complex, which recruits ATM farther from the break, which, in turn, forms γ-H2AX, and so on. Sequential assembly of MDC1 and ATM results in the propagation of γ-H2AX away from the break (29–31). While yeast lacks an MDC1 homolog, it is possible that its 53BP1 homolog, Rad9, might play a similar role in Tel1-mediated γ-H2AX spreading (32). We measured γ-H2AX spreading by Mec1 or Tel1 in the absence of Rad9 and found that the extent of phosphorylation spreading is largely unaltered for both Mec1 and Tel1, as the MMD is not significantly different in the presence and absence of Rad9 (Fig. 7 and SI Appendix, Fig. S2A). In particular, Tel1-mediated phosphorylation in rad9∆ is not significantly different from the Tel1 γ-H2AX profile in Rad9⁺ strains, suggesting that Rad9 does not contribute to a recruitment/assembly mode of γ-H2AX spreading in yeast (Fig. 7B) (29, 30, 33, 34).

Fig. 7.

γ-H2AX spreading in rad9∆ strains. (A) γ-H2AX spreading by Mec1 in rad9∆ strains. Experimental error bars represent the SEM from n = 3 measurements. (B) γ-H2AX spreading by Tel1 in rad9∆ strains. Experimental error bars represent the SEM from n = 3 measurements.

Discussion

Although we know a great deal about the evolutionarily related phosphoinositol-3-kinase like kinases ATM and ATR, including their structure and phosphorylation targets (35–37), the manner by which these kinases reach their targets has not been well characterized. Here, we used Bayesian model selection to distinguish how Mec1 and Tel1 create extended regions of γ-H2AX after DNA damage. Our analysis shows that the experimental γ-H2AX profile for Mec1 is best matched by a 3D diffusive mechanism. This is based both on the shape of the γ-H2AX profile around the DSB (Fig. 4A) and the action of Mec1 in trans (SI Appendix, Fig. S3C). However, we note that, although the 1D models cannot explain the Mec1’s phosphorylation in trans, the 1D models do produce good fits to Mec1’s γ-H2AX profile around the DSB (SI Appendix, Figs. S8–S10). Therefore, we do not rule out the possibility that Mec1 undergoes some 1D motion along the chromatin in addition to 3D diffusion.

The narrow shape of Tel1’s γ-H2AX profile around the DSB is best fit by the 1D mechanisms. Directed sliding (Fig. 4B) appears more likely than 1D diffusion (SI Appendix, Figs. S15 and S16). However, the similarity of the predicted γ-H2AX profiles for these two models leads us to not rule out 1D diffusion. γ-H2AX profile around the DSB is poorly fit by 3D diffusion, which predicts a broader profile (SI Appendix, Figs. S13 and S14).

The looping model does not match Tel1 or Mec1 dynamics. Assuming that the Kuhn length for yeast chromatin is at least 8.4 kb (38), the chromosome’s resistance to bending makes it very unlikely that a DSB-bound kinase would come into contact with a locus 5 kb from the break, The most probable contact is ≥14 kb from the DSB (SI Appendix, Fig. S17). Therefore, the looping model predicts a peaked distribution, or a flat profile if the catalytic rate is high enough to saturate all H2As (SI Appendix, Figs. S5, S6, S11, and S12). This is in disagreement with the measured γ-H2AX levels, which are maximal 2 kb to 6 kb from the break and decrease with increasing distance. While chromatin structure has been found to change following checkpoint activation (39), intrachromosomal (3C) interactions around MAT are the same before and after break formation in G1 arrested cells (40), suggesting that the Kuhn length does not change significantly after break formation. For a visual comparison of all models, see SI Appendix, Fig. S19.

The γ-H2AX profiles also provide us with insights into the recruitment process of the kinases. Since Tel1 is recruited to the nearly blunt ends created by HO endonuclease (11), whereas Mec1 requires that there be some 5′ to 3′ resection of the end (41), Tel1 would be expected to be activated before Mec1, and, indeed, this appears to be the case (Fig. 1 D–F). However, with increased expression of Ddc2, total γ-H2AX levels become comparable by 60 min (Fig. 6B). These results suggest that resection occurs rapidly enough so that enough RPA single-strand binding protein complex can bind to attract Ddc2-Mec1 soon after DSB formation.

One might also expect that, due to Tel1’s association with the MRX complex, Tel1 levels should increase in the absence of resection, since MRX is recruited to nearly blunt DNA ends, but this was not the case (Fig. 1 B and E). γ-H2AX formation was somewhat reduced in G1-arrested nej1∆ cells (where resection is impaired) compared to those in yku80∆ cells (SI Appendix, Fig. S2B). We note that there must be several MRX complexes recruited to the DSB in order that GFP-tagged proteins can be seen as a robust focus (42). It is possible that MRX-Tel1 binding is reduced by competitive binding of yKu70–yKu80, which also preferentially binds to dsDNA end (43).

ChIP measurements of Mec1-Ddc2 and Tel1 adjacent to the DSB found that they increased linearly over a time span longer than our experiments (44). While these results could indicate an accumulation of kinases at the break site, our Bayes factor calculations suggest that, even with increased kinase occupancy, the total kinase activity saturates so that the rate of phosphorylation is constant over the 75 min of our experiment. We considered both constant and increasing phosphorylation rates and found that the γ-H2AX profiles were best fit when the rate of phosphorylation remained constant over time (SI Appendix, Model Derivations and Table S1). The constant rate is assumed for all models discussed above.

The initial recruitment of Mec1 to ssDNA only confines it to sites within a few kilobases of the DSB end and does not account for the rapid spreading of γ-H2AX down the chromosome, since the rate of resection of DSB ends is only 4 kb/h (22). We note that, while γ-H2AX spreads rapidly over 50 kb from the break within an hour, H2A modifications continue to spread much more slowly over at least another 50 kb, so that modifications 100 kb from the DSB are seen only after 8 h to 10 h (45). This slower rate of modification parallels the rate of 5′ to 3′ resection and proves to be performed only by Mec1 (46). Thus, as new ssDNA is generated by the inexorable action of 5′ to 3′ exonucleases, Mec1 might reload at newly created ssDNA/RPA and proceed to diffuse from the new ssDNA to extend γ-H2AX another 50 kb.

Structural work on the Mec1-Ddc2 heterodimer suggests that it forms a stable focus at RPA-coated ssDNA with the coiled-coil domain of Ddc2 acting as a flexible linker so that Mec1 can freely phosphorylate nearby targets (28). If Mec1-Ddc2 remained at the break, then the looping mechanism would be the only possible option among the models we considered, since the other mechanisms would require the kinase to detach from the DSB after recruitment. However, our analysis shows that the predicted γ-H2AX profile from a looping mechanism does not fit the experimentally measured profile (SI Appendix, Figs. S5 and S6). In formulating the 3D mechanisms, we took into account the Kuhn length of the chromatin, as determined by both HiC and florescence microcopy experiments, and thus restricted the Kuhn length to 8.4 kb to 15 kb, the 95% CI for the Kuhn length reported by Arbona et al. (38). We assume that the Kuhn length does not change upon DNA damage, based on measurements of 3C interactions around the MAT locus both before and after a break in G1-arrested cells (40). Under these constraints, 3D diffusion is the preferred Mec1 mechanism. A 3D mechanism is further supported by γ-H2AX measurements around RE, accounting for Mec1’s ability to act in trans by phosphorylating histones on undamaged chromatin brought into close proximity with the DSB (SI Appendix, Fig. S3 A and C). Additionally, Mec1 has been shown to phosphorylate histones clustered at pericentromeric regions when a DSB is generated close to one centromere (23).

Our conclusion of Tel1 sliding is seemingly at odds with prior results that support the idea that Tel1 is tethered to the break by the MRX complex. ChIP measurements show that multiple copies of MRX (and presumably Tel1) remain associated with the DSB for 2 h to 3 h (42), much longer than the 75-min duration of our experiments. However, our analysis has shown that looping, which we associate with a DSB-bound kinase, is highly unlikely to be the mechanism employed by Tel1 (Tables 1 and 2 and SI Appendix, Fig. S1). Although Tel1 is recruited to the DSB end, its subsequent action may not depend on the MRX complex.

Results similar to 1D sliding would be predicted if chromatin near a DSB were actively extruded into a loop, a process different from the looping model in which the chromosome only undergoes passive looping due to thermal fluctuations. In vitro experiments have shown that chromatin can be actively pulled through the ring-shaped cohesin or condensin complexes, resulting in extruded chromatin loops that grow over time (47–49). Indeed, in yeast, cohesin and another SMC complex, Smc5,6, are recruited to sites of DSB damage; these recruitments require the MRX complex (50–52). We imagine a mechanism in which Tel1 remains tethered to the break while cohesin (or another SMC complex) sits near the break site and pulls in nearby chromatin through the ring. Histones pulled through the ring would therefore slide past Tel1 and be phosphorylated. Hence, the rate of loop extrusion is analogous to the rate k_slide in the sliding model. The 95% CI for k_slide overlaps with the estimated range for the speed of loop extrusion for cohesin (47). Since the rate of loop extrusion is a property of cohesin, k_slide would be unaffected by the density of phosphorylatable sites in H2A. Indeed, k_slide is unchanged in strains where only 50% of the H2As can be modified. Furthermore, loop extrusion has the added benefit of tethering Tel1 at the break end, resulting in a stable focus. Studies in mammalian cells suggests that a loop extrusion mechanism may be responsible for phosphorylation spreading, in agreement with our conclusions of a 1D sliding mechanism for Tel1 (53). It should be noted that our measurements were made with G1-arrested cells, where cohesin or other SMC complexes may not be able to assemble (50–52, 54, 55). Moreover, the profile of γ-H2AX spreading we have observed here is not apparently different from our previous observations when a DSB was induced in logarithmically growing cells (9). Additionally, spreading of γ-H2AX by Tel1 is not significantly different whether G1-arrested cells have 5′ to 3′ resection (i.e., without Yku80) or not (SI Appendix, Fig. S2). Without resection, there will not be Rad51 loading, and hence, at least, the activity of Tel1 is not a direct reflection of a Rad51-mediated search for homology (56).

After about an hour, γ-H2AX spreading is attenuated. This might suggest that there are boundary elements that constrain spreading into some adjacent region. Such boundary elements could imaginably be cohesin sites themselves. However, we have previously shown that moving a cleavage site 17 kb to the right of its original location shifted the entire profile accordingly rather than spreading over the same domain, implying that there are no boundary elements (46).

These are detailed comparisons of the mechanisms of spreading of ATM and ATR phosphorylation of histone H2A. They reveal that these two proteins, despite their evolutionary relationship, have adopted different strategies to propagate a signal away from a broken chromosome end.

Methods and Materials

Strain Construction.

All strains used were variants of the strain JKM139 (57). Standard yeast genome manipulation techniques were used to construct all strains. Linear DNA and plasmids were introduced using the standard lithium acetate transformation protocol (58, 59). The yeast strains used in this study can be found in SI Appendix, Table S2. All primer sequences and plasmids used during strain construction are listed in SI Appendix, Tables S3 and S4. Additional information regarding strain construction and growth conditions can be found in SI Appendix, Experimental Methods.

ChIP-qPCR.

ChIP was carried out according to the protocol of Shroff et al. (9) using γ-H2AX antibody (abcam ab15083). γ-H2AX levels around the DSB were assessed by qPCR using primer sequences listed in SI Appendix, Table S5. The qPCR of immunoprecipitated samples was carried out using a Rotor-Gene SYBR Green PCR Kit (Qiagen 204076) in a Qiagen Rotor-Gene Q real-time PCR machine. γ-H2AX levels at all distances around the break were normalized to input as measured at the PHO5 locus with primers MT101 and MT102.

Mathematical Modeling.

Predicted γ-H2AX profiles were simulated using the Gillespie algorithm (for the 1D diffusion model) or derived using master equations (for all other models). The models are described below and are derived in SI Appendix, Model Derivations. Three parameters are specific to each model, and an additional three parameters related to γ-H2AX recovery during ChIP are common to all models.

All models account for Mec1 or Tel1 recruitment to the DSB at a constant rate $k_{init}$. Binding of Tel1 200 bp away from a break demonstrates that Tel1 occupancy increases at a constant rate for 2 h after DSB formation (44, 60). In SI Appendix, Model Derivations, we consider the effects of kinase accumulation at DSBs, leading to increased rates of phosphorylation, while, in the main text, we only consider models with a constant rate of phosphorylation.

The 3D diffusion, 1D diffusion, and directed sliding models require activation of kinases upon arrival at DSBs. Without an activation process, these models do not predict preferential phosphorylation of H2As close to the break (see SI Appendix, Model Derivations for a further discussion of activation). A precedent for kinase activation can be found in an in vivo study of ATM autophosphorylation and activation by its association with the MRN complex (61). In budding yeast, Mec1 phosphorylates sites on its partner, Ddc2, but only does so after DSB formation, presumably when it is bound to the break (12). For simplicity, the recruitment rate $k_{init}$ encompasses this activation step. Moreover, for 1D models, $k_{init}$ also comprises the detachment of kinases from the DSB such that, for 1D models, $k_{init}$ accounts for the recruitment, activation, and detachment from the DSB.

Looping model.

We model the chromosome as a worm-like chain at thermodynamic equilibrium, which has previously been shown to predict the frequencies of physical contact between chromosomal loci in yeast (62). We assume thermodynamic equilibrium because we estimate that loci 50 kb apart come into contact every few minutes (every few seconds for loci 10 kb apart), and is much faster than the tens-of-minutes over which γ-H2AX is formed (SI Appendix, Looping Model Derivation).

The probability that the DSB-bound kinase is in contact with an H2A located x kilobases away by loop formation depends on the ratio of x to l, where l is the Kuhn length. For H2As very close to the break (x << l), the stiffness of the chromosome makes the formation of a loop highly improbable, since the energy required to bend the chromatin into a small loop is prohibitive. For H2As far from the break site (x >> l), loops are unlikely to form, since the kinase and target histones tend to occupy different regions in space. Loop formation is most probable in the regime of x ≈ l. $P_{loop}\left(x/l\right)$ is maximal at x = 1.7 l (63). The kinase phosphorylates H2A at a rate $k_{cat}$ during looping. We introduce the model parameter $\phi$, which is the product of $k_{cat}$and factors accounting for the orientation and distances required between kinases and H2A for phosphorylation. The looping model has three parameters:$k_{init},l,$ and $\phi$.

The 3D diffusion model.

Following the arrival and activation of a kinase at the DSB, the kinase leaves the break site and then diffuses along some 3D trajectory, phosphorylating the H2As with which it comes into contact. Short trajectories tend to contact H2As near the break more frequently than H2As far from the break. For longer trajectories over a longer period of time, the diffusing kinase traverses the nucleus many times over the course of the hour-long experiment, so, in the later stages of diffusion, the kinase is equally likely to hit any H2A in the nucleus. Since there are many H2As in the nucleus, we assume that the catalytic rate is only fast enough for the kinase to phosphorylate a small fraction of the H2As. Thus, kinase diffusion at late stages adds a negligible γ-H2AX signal. The predominant γ-H2AX signal comes during the early stage of diffusion, resulting in preferential phosphorylation near the break.

To predict the probability that the kinase will hit an H2A during the early stage of diffusion, we use the approximation $P_{contact}=a/R$ (64), where $a$ is the radius of the H2A and $R$ is the root-mean-squared distance from the H2A to the DSB, given by a worm-like chain model (SI Appendix, Fig. S18). $P_{contact}$ is the probability that a target of size $a$ is hit by a diffusing particle released at a distance $R$. We assume that many kinases come on and off the DSB, and $k_{leaveDSB}$ is the rate at which a kinase comes off. If kinases come off at a higher frequency, more kinases diffuse and come into contact with H2As, so phosphorylation occurs at a faster rate. The 3D diffusion model has three parameters: $k_{init},l,$ and $\omega$, where $\omega$ is a product of $k_{leaveDSB}$, $a$, and other factors that describe how likely it is that a kinase interacts with an H2A (SI Appendix, Model Derivations).

The 1D diffusion model.

In the 1D diffusion model, the chromatin fiber is treated as a 1D filament of H2As. Starting from the break site, a kinase moves along the chromatin by sliding between adjacent H2A histones. At each step, the kinase phosphorylates an H2A at a rate $k_{cat}$. The kinase is able to move away from or toward the break site with equal probability. The speed of the kinase’s motion is governed by the 1D diffusion coefficient $D$. For simplicity, we assume that the kinase does not permanently detach from the chromosome, by assuming that the time scale for falling off is greater than the duration of the experiment. Over a fixed time interval, the kinase is more likely to phosphorylate H2As that are closer to the DSB than those that are farther away, because it takes a long time for a random walk to reach a distant H2A. The simulations utilize many kinases diffusing concurrently on the chromosome (SI Appendix, Model Derivations). The parameters of the 1D diffusion model are $k_{init},D,$and $k_{cat}$.

Directed sliding model.

Similar to 1D diffusion, chromatin is treated as a 1D filament of H2A histones. Starting from the break site, the kinase slides along the chromatin at a rate $k_{slide}$ until it falls off the chromosome at a rate $k_{off}$. We assume that the kinase phosphorylates all H2As it encounters before detaching from the chromosome, and that the kinase cannot rebind to H2As that it has already phosphorylated, thereby preventing backtracking. Therefore, the kinase slides unidirectionally away from the break. In this model, H2As close to the break are more likely to be phosphorylated, because a kinase is unlikely to reach distant H2As before it falls off the chromatin. The parameters of the directed sliding model are $k_{init},k_{slide},$and $k_{off}$.

Data Availability.

All study data are included in the article and supporting information.