Figure 2.
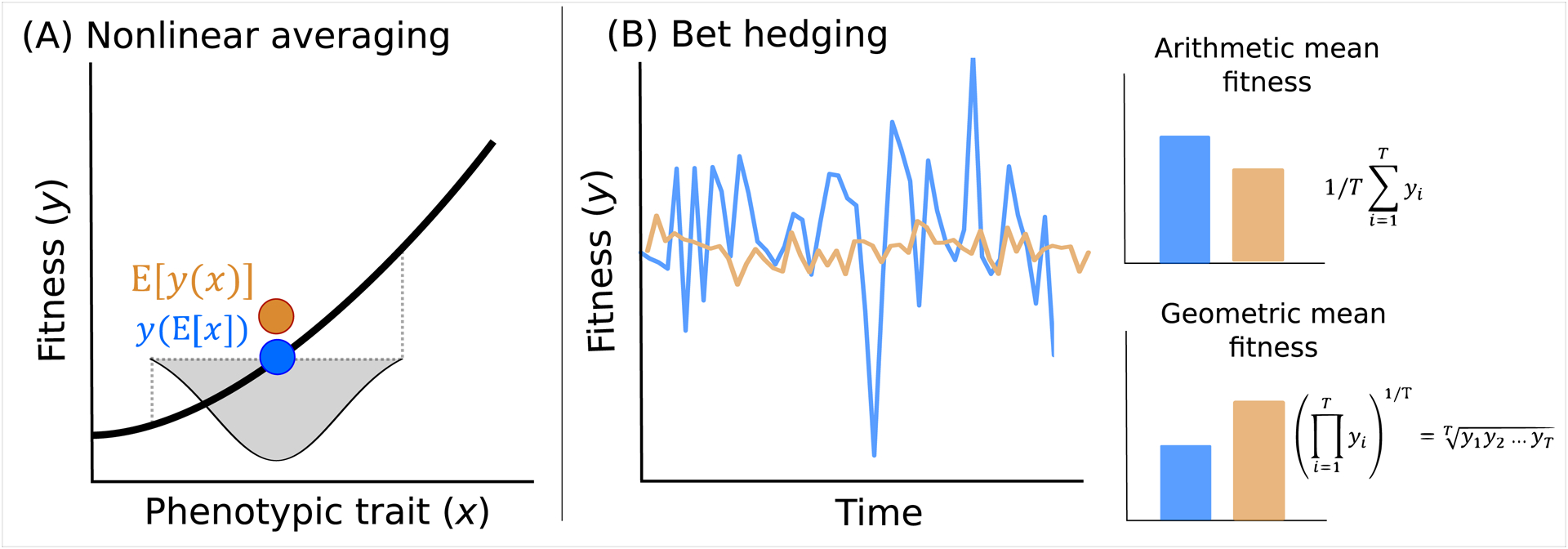
Two conditions that can result in selection favoring intra-genotypic variability: a) nonlinear averaging and b) bet hedging. a) The graph shows fitness (y) as a function of phenotype (x). If the relation is convex, an increase in the variance in x (indicated by the grey shading) results in a higher expected fitness value (E[y(x)]) (orange) than the fitness value of the average phenotype (y(E[x])) (blue), as a result of Jensen’s inequality. b) A bet hedging strategy (orange) reduces variance in fitness across generations compared to a non bet hedging strategy (blue). Despite a decrease in arithmetic mean fitness, bet hedging leads to an increase in geometric mean fitness, and is thus expected to be favored by natural selection.
